logo资料库

曲柄滑块机构的MATLAB仿真-机构运动学仿真.doc

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.25M 资料格式：doc 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    机构运动学仿真 仿真内容：滑块加速度 1r 、滑块速度 1r 、滑块位移 1r 、曲柄角速度 2 、曲柄转角 2 、 连杆角加速度 3 、连杆角速度 2 和连杆角位移 2 。下面简要陈述仿真过程。 （1） 已知的机构运动学参数 已知的机构运动学参数，包括机构原动件的运动规律和构件长度两类参数，详见表 6.3。 其中，曲柄滑块机构的原动件是曲柄，其运动规律是正态随机干扰下的曲柄角加速度 2 。 表 6.3 曲柄滑块机构的已知运动学参数 参数值 35.4 141.6  2 0 50,0N 的正态随机数 服从  机构运动学参数 r /2 mm r /3 mm /1 rad rad 2 /  s （2） 机构运动的加速度状态方程 变换式（6.5），未知的加速度项 1r 和 3 移到方程的左端，已知的曲柄角加速度 2 和其 余项移到方程的右端，它们分别作为 MATLAB Function 模块的输出和输入，则有： r  1    cos sin    1 3 1    sin r   3 3  cos r   3 3    2   2   r 2 r 2 cos sin    2 2 2    sin r    2  2 2  cos r 3  2 2       r 3 r 3 cos sin  3  3       cos sin  1  1 r  sin r    1 3 3   cos r     3 3 3        r 2 r 2 cos sin  2  2 sin r   2 2 cos r  2 2   r 3 r 3 cos sin  3  3      2   2    2   2   3      r   1     3       cos sin  1  1 1  sin r  3 3 cos r   3 3         r 2 r 2 cos sin  2  2 sin r   2 2 cos r  2 2   r 3 r 3 cos sin  3  3      2   2    2   2   3      （6.7） （3） 建立 Simulink 仿真模型 为仿真时间序列选择时钟模块；为 2 、 1 、 2r 和 3r 选择常数模块；为 1r 、 1r 及 1r ， 2 、 2 及 2 ， 3 、 3 及 3 三组有积分关系的参数选择六个积分模块；为加速度状态方程选择 MATLAB Function 模块；为数据流的合成与分解选取 Mux 和 DeMux 模块；为仿真结果的 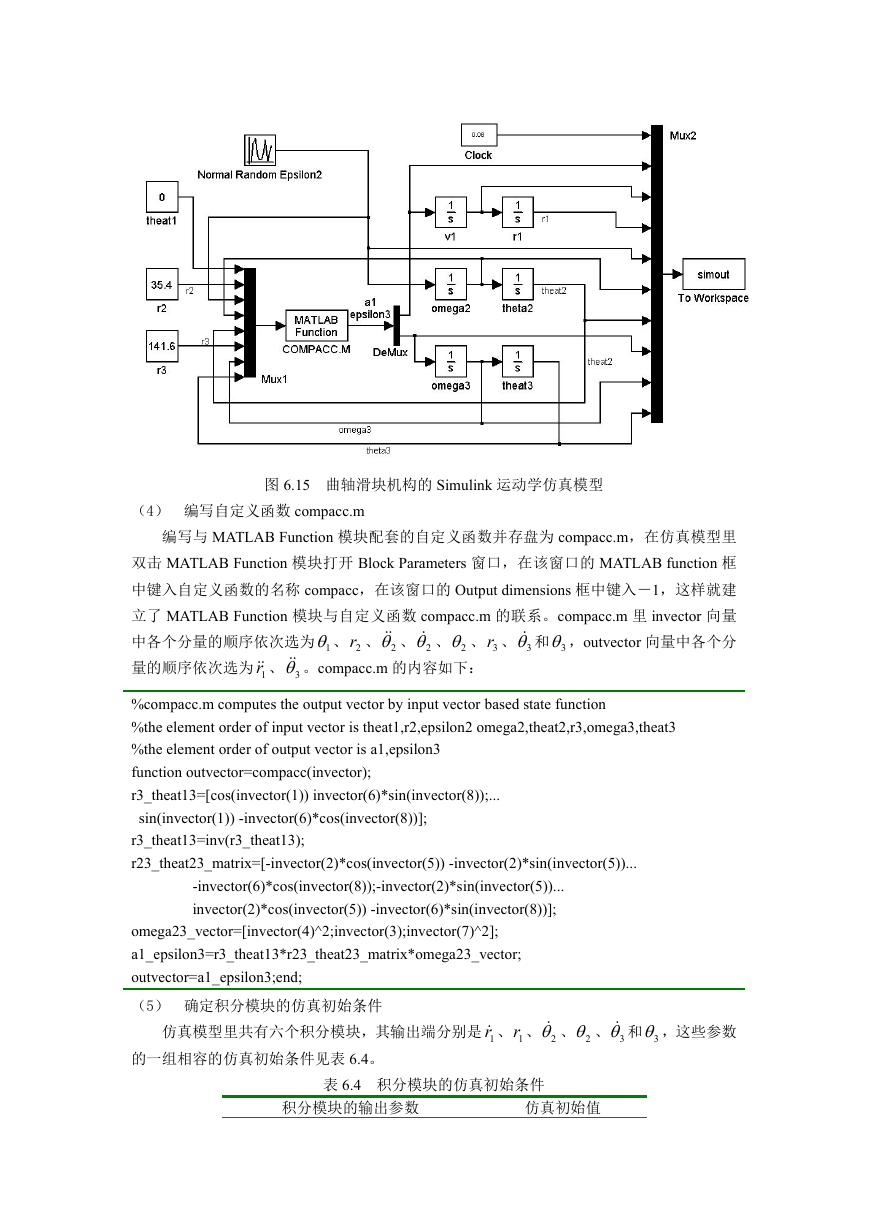记录和输出选取 simout 模块。建立的加速度仿真模型如下：
    图 6.15 曲轴滑块机构的 Simulink 运动学仿真模型 （4） 编写自定义函数 compacc.m 编写与 MATLAB Function 模块配套的自定义函数并存盘为 compacc.m，在仿真模型里 双击 MATLAB Function 模块打开 Block Parameters 窗口，在该窗口的 MATLAB function 框 中键入自定义函数的名称 compacc，在该窗口的 Output dimensions 框中键入－1，这样就建 立了 MATLAB Function 模块与自定义函数 compacc.m 的联系。compacc.m 里 invector 向量 中各个分量的顺序依次选为 1 、 2r 、 2 、 2 、 2 、 3r 、 3 和 3 ，outvector 向量中各个分 量的顺序依次选为 1r 、 3 。compacc.m 的内容如下： %compacc.m computes the output vector by input vector based state function %the element order of input vector is theat1,r2,epsilon2 omega2,theat2,r3,omega3,theat3 %the element order of output vector is a1,epsilon3 function outvector=compacc(invector); r3_theat13=[cos(invector(1)) invector(6)*sin(invector(8));... sin(invector(1)) -invector(6)*cos(invector(8))]; r3_theat13=inv(r3_theat13); r23_theat23_matrix=[-invector(2)*cos(invector(5)) -invector(2)*sin(invector(5))... -invector(6)*cos(invector(8));-invector(2)*sin(invector(5))... invector(2)*cos(invector(5)) -invector(6)*sin(invector(8))]; omega23_vector=[invector(4)^2;invector(3);invector(7)^2]; a1_epsilon3=r3_theat13*r23_theat23_matrix*omega23_vector; outvector=a1_epsilon3;end; （5） 确定积分模块的仿真初始条件 仿真模型里共有六个积分模块，其输出端分别是 1r 、 1r 、 2 、 2 、 3 和 3 ，这些参数 的一组相容的仿真初始条件见表 6.4。 表 6.4 积分模块的仿真初始条件 积分模块的输出参数 仿真初始值
    r /1 mm 1 /  smm r /2 rad rad 2 /  s /3 rad rad 3 /  s  1  1  1 177 0 0 209.4395 0 －52.3599 在仿真模型里分别双击标签为 v1、r1、omega2、theat2、omega3 和 theta3 的模块（这些 模块对输入参数积分后输出参数 1r 、1r 、 2 、 2 、 3 和 3 ），分别打开它们的 Block Parameters 窗口，根据表 6.4 在 Initial condition 框中分别键入仿真初始值 177、0、0、209.4395、0 和－ 52.3599。 （6） 观察仿真结果 选择仿真两个机构运动周期，根据曲柄转速 ，所需仿真时间为 0.06s， 设置仿真时间 0.06s 并运行 Simulink 仿真模型。SpaceWork 中的变量 simout 记录了仿真结果， 可编写一个如下所示的程序，将仿真结果以图形方式显示。 209 . 4395 2  close all; figure,plot(simout(:,1),simout(:,2)/1000);grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('活塞加速度 m/s^2','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,3)/1000);grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('活塞速度 m/s','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,4)/1000);grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('活塞位移 m','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,5));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('曲柄角加速度 rad/s^2','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,6));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('曲柄角速度 rad/s','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,7));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('曲柄转角 rad','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,8));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('连杆角加速度 rad/s^2','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,9));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman');
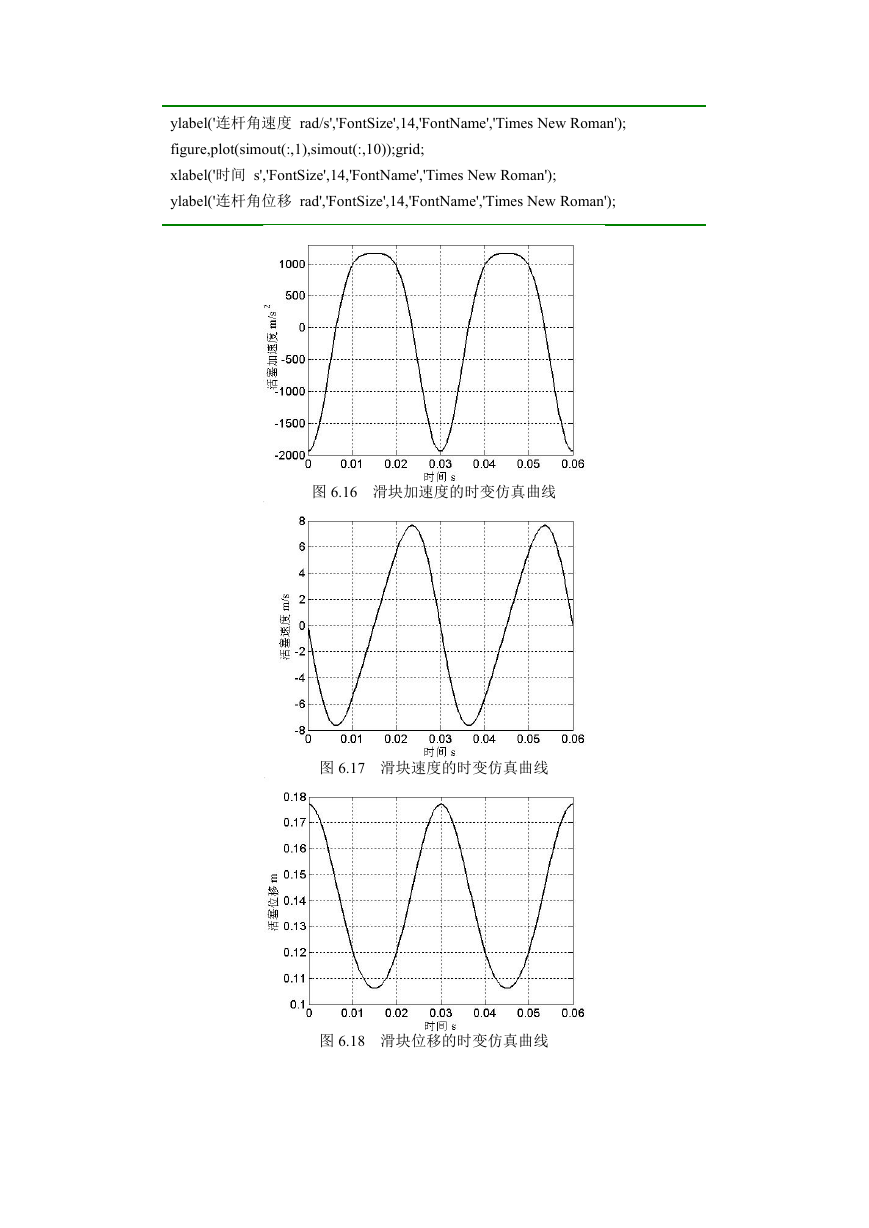
    ylabel('连杆角速度 rad/s','FontSize',14,'FontName','Times New Roman'); figure,plot(simout(:,1),simout(:,10));grid; xlabel('时间 s','FontSize',14,'FontName','Times New Roman'); ylabel('连杆角位移 rad','FontSize',14,'FontName','Times New Roman'); 图 6.16 滑块加速度的时变仿真曲线 图 6.17 滑块速度的时变仿真曲线 图 6.18 滑块位移的时变仿真曲线
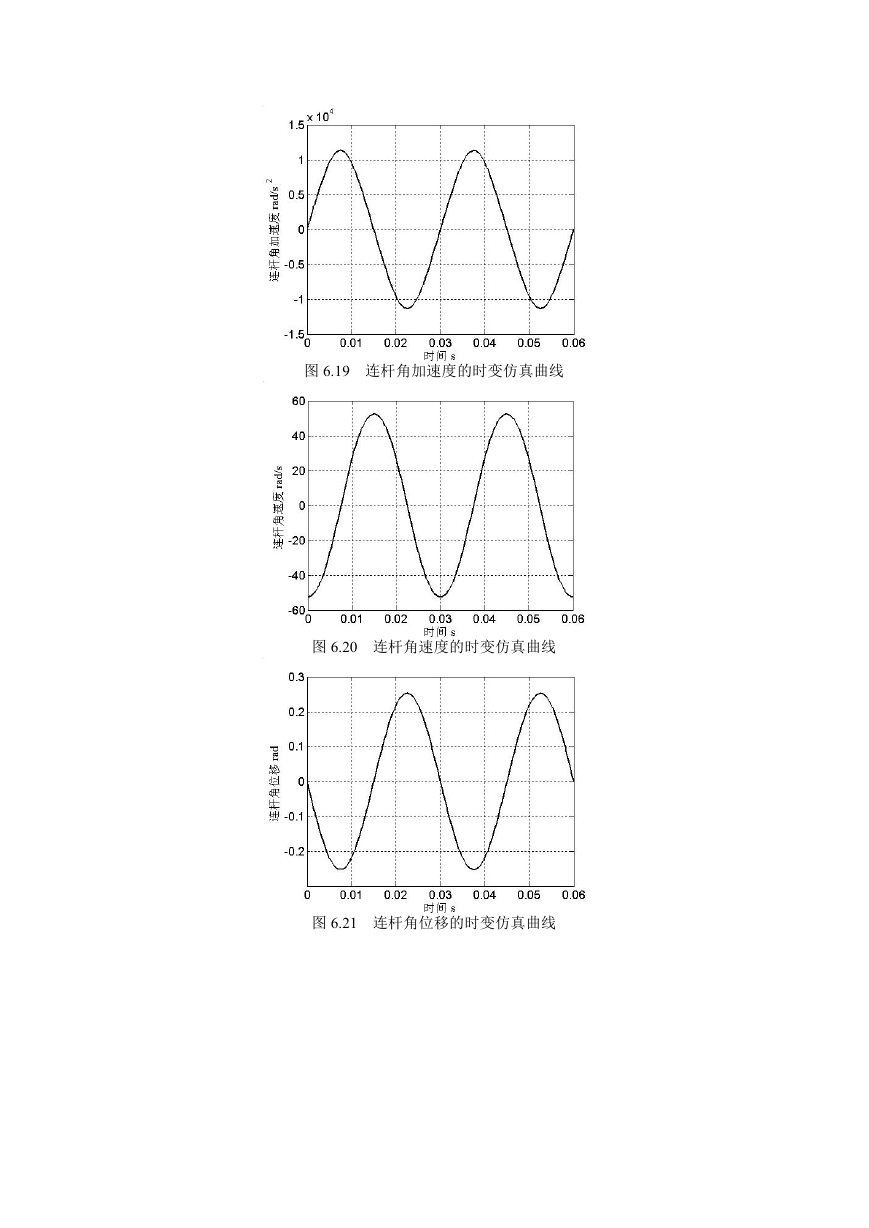
    图 6.19 连杆角加速度的时变仿真曲线 图 6.20 连杆角速度的时变仿真曲线 图 6.21 连杆角位移的时变仿真曲线
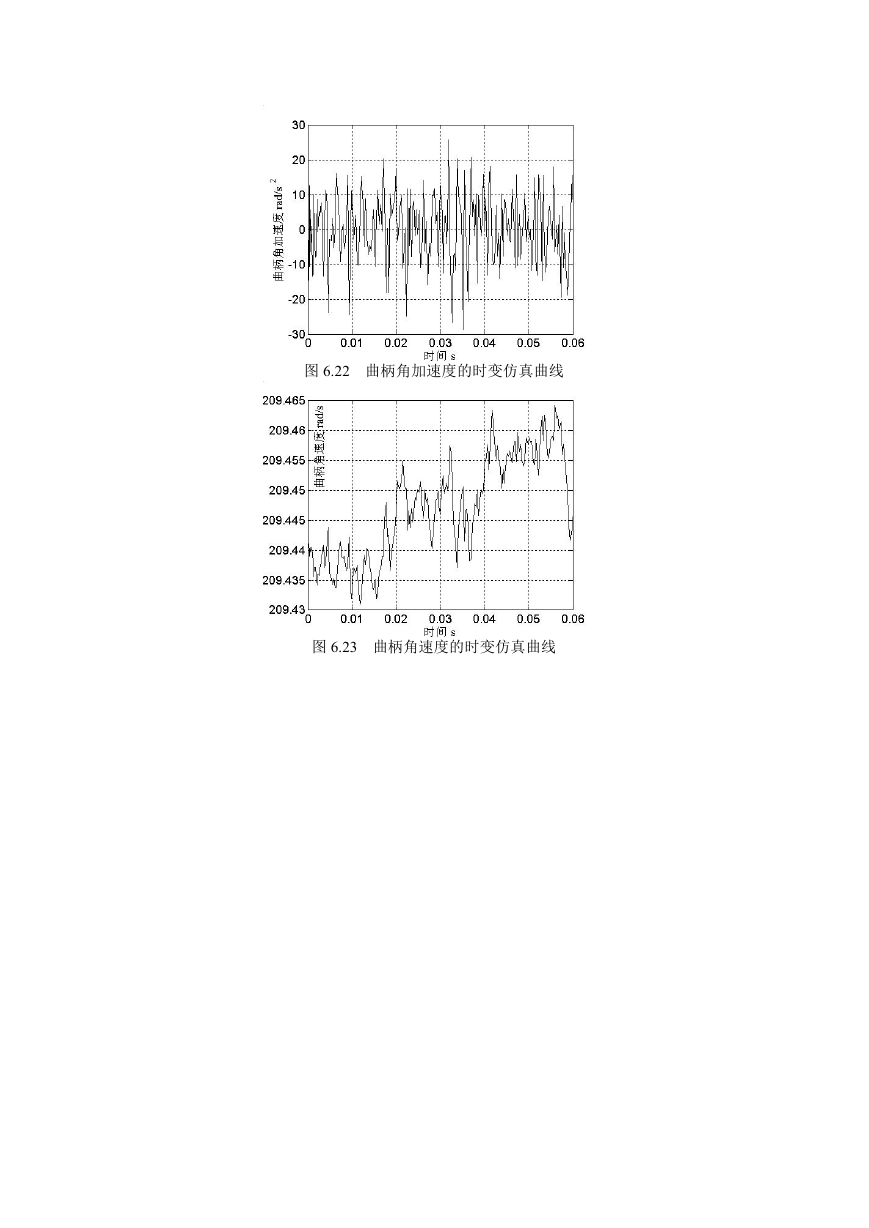
    图 6.22 曲柄角加速度的时变仿真曲线 图 6.23 曲柄角速度的时变仿真曲线
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料