Learning representations by back propagating errors(1985).pdf-资料库

(V) two LEARNING INTERNAL REPRESENTATIONS BERROR PROPAGATION David E. Ruineihart, Geoffrey E. Hint.., and Ronald J. Williams 0 4 September 1985 ICS Report 8506 COGNITIVE SCIENCE IaQ I INSTITUTE FOR COGNITIVE SCIENCE UNIVERSITY OF CALIFORNIA, SAN DIEGO 862 18 LA JOLLA, CALIFORNIA 92093 120,

4- U-

LEARNING INTERNAL REPRESENTATIONS BY ERROR PROPAGATION David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams DTIC September 1985 ICS Report M50 SLD AL"LECT FEB 20 M David E. Rumelhart Institute for Cognitive Science University of California, San Diego Geoffrey E. Hinton Department of Computer Science Carnegie-Mellon University Ronald J. Williams Institute for Cognitive Science University of California, San Diego Di' _ AL xow"d io n publ@ DkltAtfikuim fi1Id To be published in D. E. Rumelhart & i. L. McClelland (Eds.), Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Vol. 1: Foundations. Cambridge, MA: Bradford Books/MIT Press. This research wa supported by Contract NOD14.45-K0450, NR 667-58 with the Personnel Lad Training Research Pro- gams of the Office of Naval Research and by grants from the System Development Foundation. Requests for rm- prints siould be seat to David E. Ramdhut, Institute for Cognitive Science, C4)13; University of California, San Diego; La Jolla, CA 92093. Copyright 0 1985 by David B. Rumeliat, Geoffrey E. finton. and Ronald i. Williams U P.

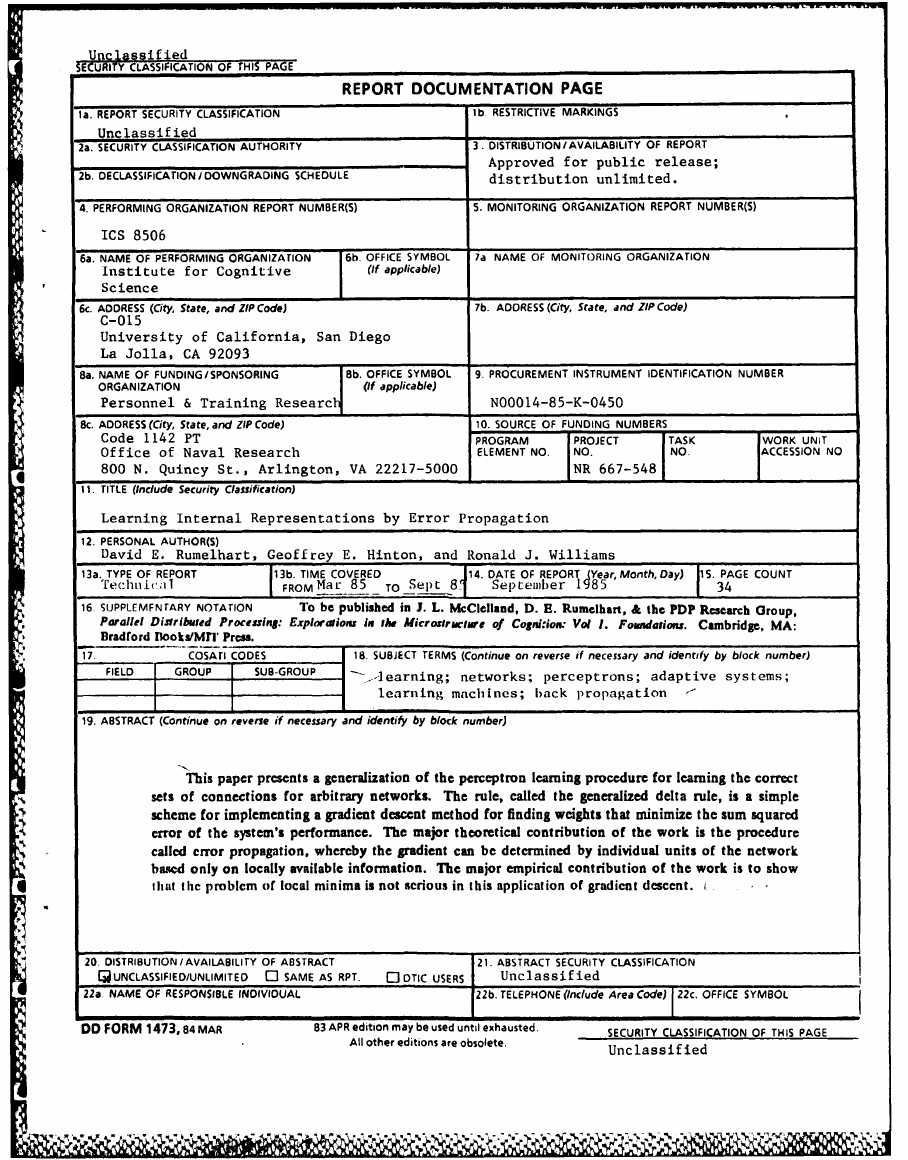
Unclassified SECURITY CLASSIFICATION OF THIS PAGE REPORT DOCUMENTATION PAGE la. REPORT SECURITY CLASSIFICATION Unclassified 2a. SECURITY CLASSIFICATION AUTHORITY 2b. DECLASSIFICATION I DOWNGRADING SCHEDULE lb RESTRICTIVE MARKINGS 3. DISTRIBUTION/AVAILABILITY OF REPORT Approved for public release; distribution unlimited. ,, 4. PERFORMING ORGANIZATION REPORT NUMBER(S) S. MONITORING ORGANIZATION REPORT NUMBER(S) ICS 8506 6a. NAME OF PERFORMING ORGANIZATION Institute for Cognitive Science I 6b. OFFICE SYMBOL (If applicable) 6c. ADDRESS (City, State, and ZIP Code) C-015 University of California, San Diego La Jolla, CA 92093 Ba. NAME OF FUNDING/SPONSORING ORGANIZATION Personnel & Training Researc 8b. OFFICE SYMBOL (If applicable) 8c. ADDRESS (City, State, and ZIP Code) Code 1142 PT Office of Naval Research 800 N. Quincy St., Arlington, VA 22217-5000 11. TITLE (Include Security Classification) 7a NAME OF MONITORING ORGANIZATION 7b. ADDRESS (City, State, and ZIP Code) 9. PROCUREMENT INSTRUMENT IDENTIFICATION NUMBER N00014-85-K-0450 10. SOURCE OF FUNDING NUMBERS PROGRAM ELEMENT NO. PROJECT NO. NR 667-548 TASK NO. WORK UNiT ACCESSION NO Learning Internal Representations by Error Propagation 12. PERSONAL AUTHOR(S) David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams 13a. TYPE OF REPORT Technical 13b. TIME COVERED FROMMar 85 TO Sept 8 14. DATE OF REPORT (ear, Month, Day) S. PAGE COUNT September 1985 34 16 SUPPLEMFNTARY NOTATION To be published in J. L. McClelland, D. E. Rumelhart, & the PDP Research Group, Parallel Dislribuled Processing: Exploratiois in the Microstrucure of Cognkion: Vol 1. Founsdations. Cambridge, MA: Bradford nlooks/Mnr Press. 17. COSATI CODES FIELD GROUP SUB-GROUP 18. SUBJECT TERMS (Continue on reverse if necessary and identify by block number) -learning; networks; perceptrons; adaptive systems; learning machines; back propagation 19. ABSTRACT (Continue on reverse if necessary and identify by block number) This paper presents a generalization of the perceptron learning procedure for learning the correct sets of connections for arbitrary networks. The rule, called the generalized delta rule, is a simple scheme for implementing a gradient descent method for finding weights that minimize the sum squared error of the system's performance. The major theoretical contribution of the work is the procedure called error propagation, whereby the gradient can be determined by individual units of the network based only on locally available information. The major empirical contribution of the work is to show that thc problem of local minima is not serious in this application of gradient descent. i 20. DISTRIBUTION/AVAILABILITY OF ABSTRACT QUNCLASSIFIED/UNLIMITED 0 SAME AS RPT. 21. ABSTRACT SECURITY CLASSIFICATION 0 DTIC USERS Unclassified 22a NAME OF RESPONSIBLE INDIVIDUAL 22b. TELEPHONE (Include Area Code) 22c. OFFICE SYMBOL DO FORM 1473, 84 MAR 83 APR edition may be used until exhausted. All other editions are obsolete. SECURITY CLASSIFICATION OF THIS PAGE Unclassified

Contents THE PROBLEM ................................................................................. THE GEN4ERALIZED DELTA RULE........................................................ The delta rule and gradient descent................................................ The delta rule for semilinear activation functions in feedforward networks. S[MULATION RESULTS ..................................................................... A useful activation function .......................................................... The learning rate..................................................................... Symmetry breaking................................................................... The XOR Problem........................................................................ Parity ................................................................................... The Encoding Problem................................................................... Symmetry ............................................................................... Addition ................................................................................ Negation Problem.................................................................... *The The T-C Problem .......................................................................... More Simulation Results................................................................. SOME FURTHER GENERALIZATIONS ................................................... The Generalized Delta Rule and Sigma-Pi Units .................................... Recurrent Nets......................................................................... Leff nng to be a shift register ...................................................... Learning to complete sequences ..................................................... CONCLUSION................................................................................... REFERENCES................................................................................ 4 4 5 8 8 9 10 10 12 14 17 18 21 22 26 26 26 2 29 30 31 33 Uiannoun'ced 13

Learning Internal Representations by Error Propagation DAVID E. RUMELHART, GEOFFREY E. HINTON, and RONALD J. WILLIAMS THE PROBLEM We now have a rather good understanding of simple two-layer associative networks in which a set of input patterns arriving at an input layer are mapped directly to a set of output patterns at an output layer. Such networks have no hidden units. They involve only input and owput units. In these cases there is no internal represenatmon. The coding provided by the external world must suffice. These networks have proved useful in a wide variety of applications (cf. Chapters 2, 17, and 18). Perhaps the essential character of such networks is that they map simi- lar input patterns to similar output patterns. This is what allows these networks to make rea- sonable generalizations and perform reasonably on patterns that have never before been presented. The similarity of patterns in a PDP system is determined by their overlap. The overlap in such networks is determined outside the learning system itself-by whatever pro- duces the patterns. The constraint that similar input patterns lead to similar outputs can lead to an inability of the system to learn certain mappings from input to output. Whenever the representation pro- vided by the outside world is such that the similarity structure of the input and output pat- tcrns are very different, a network without internal representations (i.e., a network without hidden units) will be unable to perform the necessary mappings. A classic example of this case is the exclusive-or (XOR) problem illustrated in Table 1. Here we see that those patterns which overlap least arc supposed to generate identical output values. This problem and many others like it cannot be performed by networks without hidden units with which to create TABLE I Input Patterns Output oPatterns 01 -0

2 RUMELHART. HrwrON. and WILLIAMS TABLE 2 Input Patterns Output Patterns 00 010 11 - 0 1. 0 their own internal representations of the input patterns. It is interesting to note that had the input patterns contained a third input taking the value 1 whenever the first two have value 1 as shown in Table 2, a two-layer system would be able to solve the problem. Minsky and Papert (1969) have provided a very careful analysis of conditions under which such systems are capable of carrying out the required mappings. They show that in a large number of interesting cases, networks of this kind are incapable of solving the problems. On the other hand, as Minsky and Papert also pointed out, if there is a layer of simple perceptron- like hidden units, as shown in Figure 1, with which the original input pattern can be aug- mented, there is always a recoding (i.e., an internal representation) of the input patterns in the hidden units in which the similarity of the patterns among the hidden units can support any required mapping from the input to the output units. Thus, if we have the right connections from the input units to a large enough set of hidden units, we can always find a representation Output Patterns Internal O" *Representation Units Input Patterns FIGURE 1. A multilayer network. In this case the information coming to the input units is receded into an inter- nal representation and the outputs are generated by the internal representation rather than by the original pattern. Input patterns can always be encoded, if there are enough hidden units, in a form so that the appropriate output pat- tern can be generated from any input pattern. 6 M

LEARNING miNLRNAL REPRE ENTATIONS 3 that will perform any mapping from input to output through these hidden units. In the case of the XOR problem, the addition of a feature that detects the conjunction of the input units changes the similarity structure of the patterns sufficiently to allow the solution to be learned. As illustrated in Figure 2, this can be done with a single hidden unit. The numbers on the arrows represent the strengths of the connections among the units. The numbers written in the circles represent the thresholds of the units. The value of +1.5 for the threshold of the hidden unit insures that it will be turned on only when both input units are on. The value 0.5 for the output unit insures that it will turn on only when it receives a net positive input greater than 0.5. The weight of -2 from the hidden uait to the output unit insures that the output unit will not come on when both input units arc on. Note that from the point of view of the output unit, the hidden unit is treated as simply another input unit. It is as if the input patterns consisted of three rather than two units. The existence of networks such as this illustrates the potential power of hidden units and internal representations. The problem, as noted by Minsky and Papert, is that whereas there is a very simple guaranteed learning rule for all problems that can be solved without hidden units, namely, the perceptron convergence procedure (or the variation due originally to Widrow and Hoff, 1960, which we call the delta rule; see Chapter 11), there is no equally powerful rule for learning in networks with hidden units. There have been three basic responses to this lack. One response is represented by competitive learning (Chapter 5) in which simple unsupervised learning rules are employed so that useful hidden units develop. Although these approaches are promising, there is no external force to insure that hidden units appropriate for the required mapping are developed. The second response is to simply asswne an internal representation that, on some a priori grounds, seems reasonable. This is the tack taken in the chapter on verb learning (Chapter 18) and in theinteractive activation model of word perception (McClelland & Rumelhart, 1981; Rumelhart & McClelland, 1982). The third approach is to attempt to develop a learning procedure capable of learning an internal representation adequate for per- forming the task at hand. One such development is presented in the discussion of Boltzmann machines in Chapter 7. As we have seen, this procedure involves the use of stochastic units, requires the network to reach equilibrium in two different phases, and is limited to symmetric networks. Another recent approach, also employing stochastic units, has been developed by Barto (1985) and various of his colleagues (cf. Barto & Anandan, 1985). In this chapter we .5 Output Unit +1 -21 +1 Hidden Unit S +1 +1 Input Units FIGURE 2. A simple XOR network with one hidden unit. See text for explanation. d '% .. - P I .

资料库

Learning representations by back propagating errors(1985).pdf

相关推荐

人工智能

热门标签

最新资料