第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
牛顿法，牛顿下山，割线法，高斯消去法，列主元高斯消去，LU分解法matlab源程序.doc
实验报告
课程名称：
数 值 分 析
实验项目：
解 方 程 / 解 方 程 组
专业班级：
检测技术与自动化装置
姓
名：
韦晔
学
号： 201810326
实验室号：
实验组号：
实验时间：2018/10/21 批阅时间：
指导教师：
张琪
成
绩：
沈阳工业大学实验报告
（适用计算机程序设计类）
专业班级： 检测技术与自动化装置 学号： 201810326
姓名： 韦晔
实验名称：解方程
1.实验目的：
1.掌握用 Newton 迭代法，简化牛顿法，牛顿下山法和割线法求解方程。
2.用编程实现算法（本次实验平台为 matlab）。
2.实验内容：
解方程选择第一题：
1. 分别用牛顿法、简化牛顿法，牛顿下山法和割线法求解方程
( )
f x
x
xe
1 0
3. 实验方案（程序设计说明）
牛顿法的算法设计思路：欲求某方程 f(X) = 0 的根，按照以下步骤进行求解： 令 X0 =
0.5（也可以选择其他值） i = 0, 1, 2…..
（1）、求出 f（xi）和导数 df（xi）
（2）、令 xi+1 = xi - f（xi）/ df（xi）
（3）、将 xi+1 带入方程 f(X) 计算方程值，当方程值与目标值的误差小于预定值时，退出
算法输出 xi+1 即为方程根，否则退回（1）步继续计算。
牛顿简化法算法思路：在牛顿法基础上，将导数 df（xi）固定成一个数 M，其他思路不
变。
牛顿下山法算法思路：取λ=1，使得 xi+1= xi – λ*f（xi）/ df（xi），然后将λ逐半减小，
一直到|f(xi+1)|< |f(xi)|，其他的大部分与牛顿法相同。
割线法算法思路：为了避免计算 df（xi），将 df（xi）=（f(xi)- f(xi-1)）/(xi-xi-1)。再带
入牛顿迭代公式即可。
**流程图见附件 A
变量说明：
编程中，将 f=x*（exp（x）），x0 为输入的初始值，k 为迭代次数，返回最后的 x 和 k。
具体的变量说明参见编程代码
4. 实验步骤或程序（经调试后正确的源程序）
在 matlab 的 command 窗口输出:
syms x；
1
f=x*exp（x）-1；
[x k]=ND1(f,0.5,10^-6);(牛顿法)
[x k]=ND2(f,0.5,10^-6);(简化牛顿法)
[x k]=ND3(f,0.5,10^-6);(牛顿下山法)
[x k]=ND4(f,0.5,10^-6);(割线法)
5．程序运行结果
x=0.5671,k=4;牛顿法
x=0.5671,k=6;简化牛顿法
x=0.5710,k=1;牛顿下山法
x=0.5671,k=4;割线法
6．出现的问题及解决方法
1.不熟悉各种函数的使用，通过 matlab help – 命令查函数用法。
2.算法流程不熟练，编程期间的 bug 通过调试解决。
2
附件 A
沈阳工业大学实验报告
（适用计算机程序设计类）
专业班级： 检测技术与自动化装置 学号： 201810326
姓名： 韦晔
实验步骤或程序：
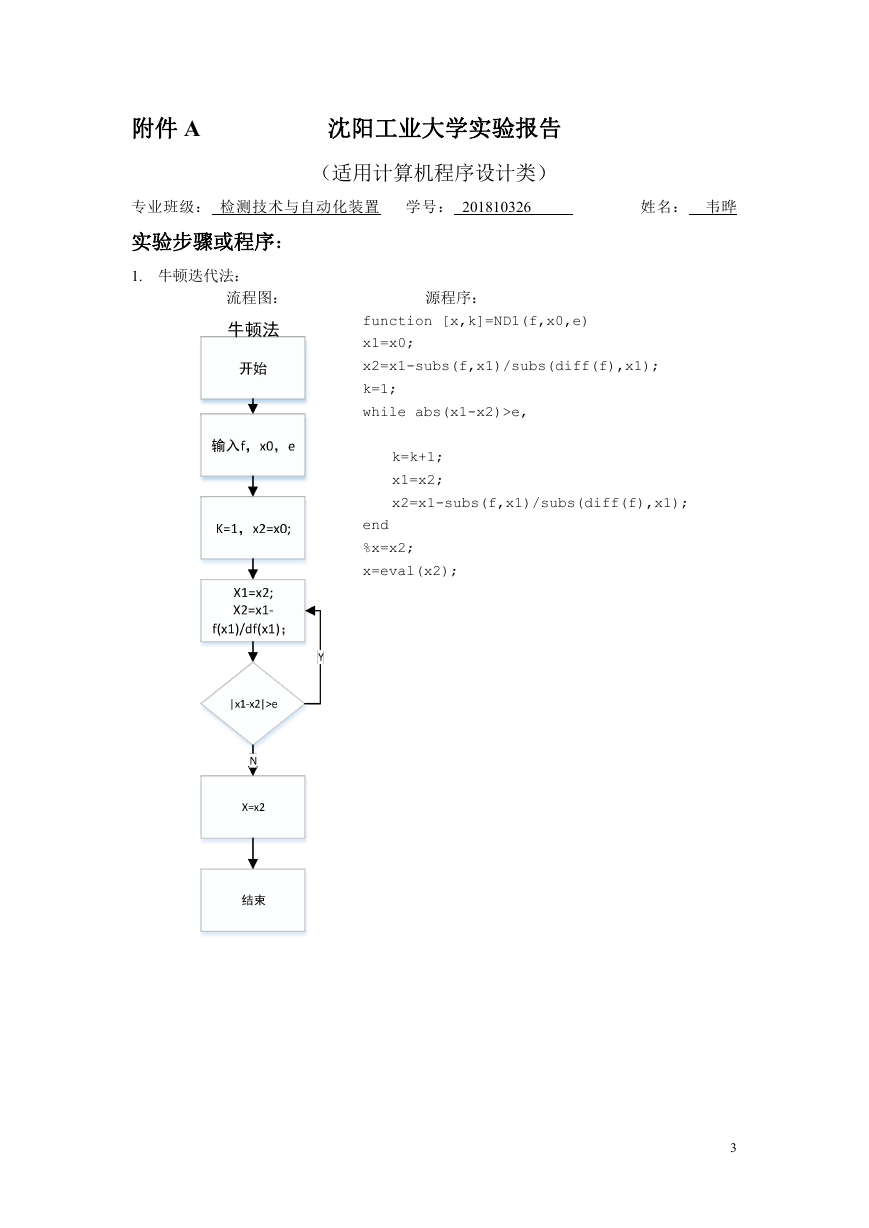
1. 牛顿迭代法：
流程图：
源程序：
function [x,k]=ND1(f,x0,e)
x1=x0;
x2=x1-subs(f,x1)/subs(diff(f),x1);
k=1;
while abs(x1-x2)>e,
k=k+1;
x1=x2;
x2=x1-subs(f,x1)/subs(diff(f),x1);
end
%x=x2;
x=eval(x2);
3
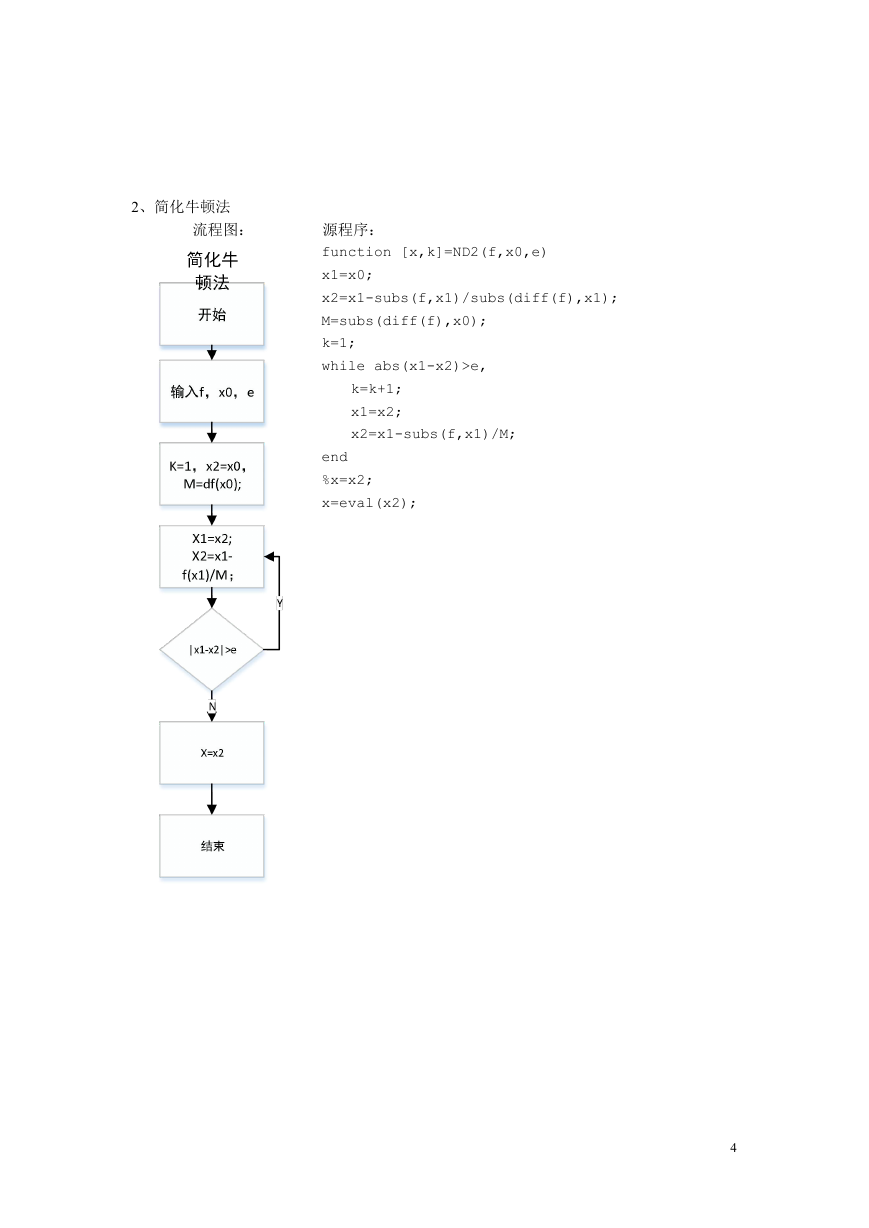
2、简化牛顿法
流程图：
源程序：
function [x,k]=ND2(f,x0,e)
x1=x0;
x2=x1-subs(f,x1)/subs(diff(f),x1);
M=subs(diff(f),x0);
k=1;
while abs(x1-x2)>e,
k=k+1;
x1=x2;
x2=x1-subs(f,x1)/M;
end
%x=x2;
x=eval(x2);
4
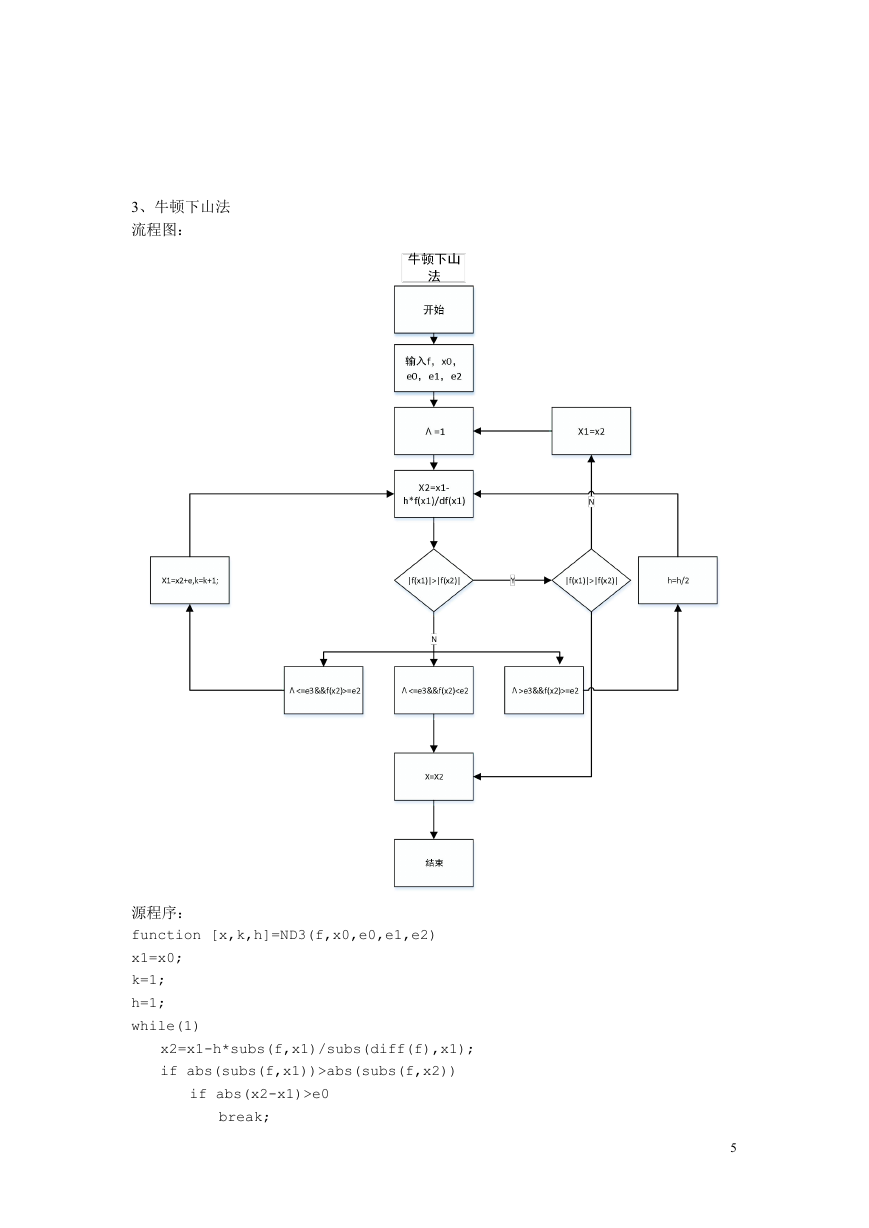
3、牛顿下山法
流程图：
源程序：
function [x,k,h]=ND3(f,x0,e0,e1,e2)
x1=x0;
k=1;
h=1;
while(1)
x2=x1-h*subs(f,x1)/subs(diff(f),x1);
if abs(subs(f,x1))>abs(subs(f,x2))
if abs(x2-x1)>e0
break;
5
end
if (h<=e2)&&(subs(f,x2)=e1)
elseif (h>e2)&&(subs(f,x2)>=e1)
end
x1=x2;
h=1;
break;
x1=x2+e0;
k=k+1;
h=h/2;
k=k+1;
end
end
x=eval(x2);
end
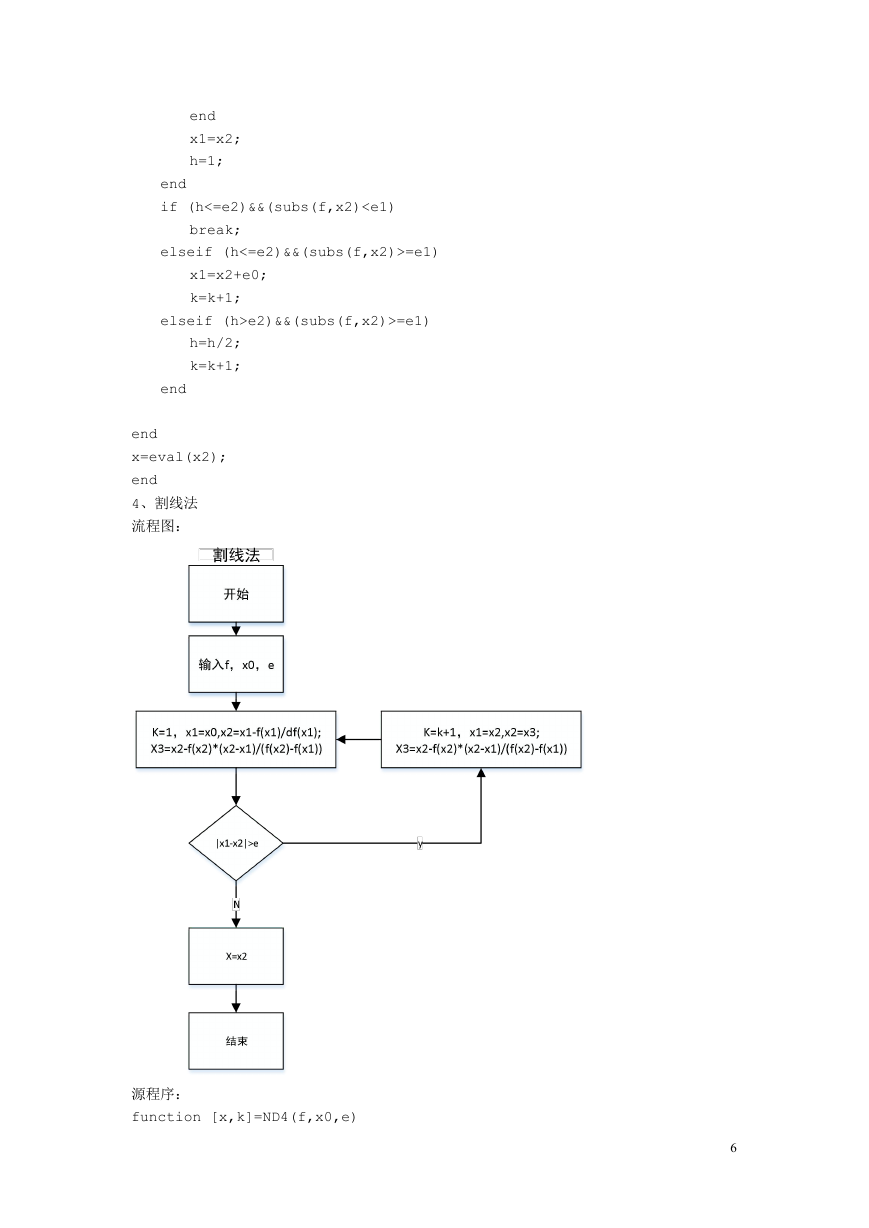
4、割线法
流程图：
源程序：
function [x,k]=ND4(f,x0,e)
6
x1=x0;
x2=x1-subs(f,x1)/subs(diff(f),x1);
x3=x2-subs(f,x1)*(x2-x1)/(subs(f,x2)-subs(f,x1));
k=1;
while abs(x3-x2)>e,
k=k+1;
x1=x2;
x2=x3;
x3=x2-subs(f,x2)*(x2-x1)/(subs(f,x2)-subs(f,x1));
end
x=eval(x3);
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
