logo资料库

基于加权组合规则和仿真的动态多目标生产调度.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.31M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 基于加权组合规则和仿真的动态多目 标生产调度# 马丽梅，李建勇，徐文胜** （北京交通大学机械与电子控制工程学院，北京 100044） 摘要：可重构制造系统生产调度的特点是根据加工任务的变化对制造系统进行重构。针对具 有多约束、多目标的柔性工作车间系统重构的调度问题，基于系统资源配置、任务约束以及 调度目标，设计了基于多种调度规则加权组合的多目标实时调度算法。该算法克服了传统规 则简单组合在解决多目标调度问题时难以确定较优组合方案的缺点，保持了规则调度算法的 简单易行等特点。同时，基于该调度算法对车间资源配置进行了重构，获得了最优的配置方 案。最后，利用 Flexsim 软件建模仿真验证了该算法的可行性和有效性。 关键词：调度规则；加权组合；多目标优化；资源配置；仿真 中图分类号：TH165；TP391 Dynamic and Multi-objective Scheduling Based on Weighted Combined Rules and Simulation MA Limei, LI Jianyong, XU Wensheng (School of Mechanical and Electronic Control Engineering, Beijing Jiaotong University, Beijing 100044) Abstract: Production scheduling of Reconfigurable manufacturing systems is characterized by changing system configuration according to machining tasks. In order to solve multi-constrains and multi-objective flexible job shop system scheduling problem, a multi-objective and real-time scheduling algorithm was presented based on resource configuration, task constrains and scheduling objectives. It overcomes the traditional difficulty to find optimal combined rules for multi-objective, meanwhile keeps the simpleness of the scheduling rules. At the same time, resource configuration schemes were generated based on the presented algorithm and the optimal scheme was selected. Finally, Flexsim software modeling and simulation method was used to validate its feasibility and effectiveness. Keywords: Scheduling Rules; Weighted Combination; Multi-Objective Optimization; Resource Configuration; Simulation (RMS) 0 引言 可重构制造系统（Reconfigurable Manufacturing Systems，RMS）是面向动态市场需求的 既具有定制的柔性又具有高生产率的新型制造系统[1]。ELMaraghy 等人将制造系统重构分为 两类，基于硬件的重构与基于软件的重构，硬件重构包括增加/移除设备、机床模块及其改 变物料传送系统；软件重构包括机床的重编程、重规划、重调度、增加/降低工人数量与班 次等[2-4]。调度是解决生产和服务系统多任务需求分配和排序的重要环节，调度方案的优劣 对整个系统的运作性能有着重大的影响[5]。调度问题的一大特点是模型繁多，对于适应于某 一模型的算法，只要将模型的环境稍加变化，算法就不再适用。基于规则的方法简单易行， 可避免求解解析模型的复杂性，被企业广泛采用[6]。He & Hui 研究了面向并行机环境的基于 规则的启发式遗传算法[7]，Jayamohan 等提出了面向工作车间的基于成本调度规则的调度算 基金项目：教育部高校博士点专项科研项目基金（200800040018）；国家自然科学基金（51175033） 作者简介：马丽梅，（1982-），女，博士生，主要研究方向：产品优化配置、网络联盟、可重构机床。 通信联系人：李建勇，（1962-），男，教授，主要研究方向：先进制造过程与系统、机电系统控制及自动 化、数控技术与计算机辅助制造、智能工程与先进设计理论. E-mail: Jyli@bjtu.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn 45 50 法[8]等。金锋赫等研究了基于设备可用时间约束的装配作业车间组合调度规则[9]。 实时调度算法是在变化的环境中做出反应，这类算法应用比较灵活，适合于任务不断生 成，并且在任务生成之前其特性未知的动态实时系统[10]。不同调度规则和路径选择规则的 组合会产生性能差异很大的调度方案，因此需要根据调度目标从方案集合中选出合理的调度 方案[11, 12]。在仿真领域，金淳等提出了基于离散事件系统仿真模型与 Tabu 搜索启发式算法 相结合的调度优化算法[13]。目前国内外研究人员主要通过仿真方法评价调度规则在单一性 能指标上的优越性，对在多个指标下如何选取最优调度规则以及如何基于调度方案对制造系 统的重构进行规划的研究较少[14]。针对上述问题，作者以可重构制造系统为背景，研究了 任务具有多种约束、及多目标的调度问题，提出了一种基于仿真的调度规则加权组合的多目 标实时调度方法，并基于该方法对制造系统的规划方案进行评估与优选。 1 调度问题描述与模型建立 1.1 问题描述 55 调度问题是典型的多目标决策问题，研究表明，调度规则的选取取决于系统资源配置、 任务约束以及调度目标[6]。因此在选择调度规则前，首先要对调度问题进行分析。可重构制 造系统生产调度的特点是根据加工任务的变化对制造系统进行重构，除了需要确定加工任务 的顺序、任务路径选择规则、任务分派规则之外，还需要对系统资源进行重新配置。本文对 具有多种约束的加工任务进行分析，基于资源配置与多调度目标，在确定加工任务顺序、任 务分配的同时，对资源配置进行重新部署，以达到最优的调度目标，如图 1 所示。 加工任务约束 资源配置 到达时间 处理时间 优先级 ... 生产调度目标 最小化延期任 务数量 最小化任务延 期总时间 均衡工程师任 务量 ... 输入 基于仿真的调度规 则加权组合的多目 标实时调度方法 输出 资源重配置方案 加工任务排序 资源任务分配 列表 60 图 1 生产调度流程框架 Fig. 1 the Framework of Scheduling Flow 在此，考虑以多订单多任务为特点的某 IT 商务技术支持部门优化调度问题。工程师要 65 处理的任务有以下几种约束： （1）任务生成状态，部门的任务需求是动态产生的。 （2）任务到达时间（Arrival Time），每个订单由一项或多项任务需求组成，即订单与 - 2 -
    中国科技论文在线 其各项任务具有相同的到达时间。 http://www.paper.edu.cn （3）任务路径(Route)与任务总流程量（Total flow Number），如图 2 所示，以有向图 表示其任务路径，节点 0 表示订单生成即任务需求产生，节点 1 与 2 表示任务所需的不同资 源，节点 3 表示任务的结束即服务完成。每个任务的流程并不是相同的，有三种流程：0->1->3、 0->2->3、0->1->2->3，其任务总流程量为 1、1、2。 图 2 不同任务的流程图 Fig. 2 Flow for Different Tasks 70 75 （4）优先级（Priority），任务根据顾客身份的不同分为三个的优先级：1 为 VIP 顾客 订单生成的任务，2 为紧急的任务，3 为一般普通的任务，优先级从 1 至 3 依次降低。同一 订单内部任务的优先级相同，任务必须按照任务优先级的高低顺序操作。 80 （5）任务处理时间(Process Time)，工程师一次只能处理一项任务，直至该任务处理完 工程师才能空闲，即处理过程不可中断。 （6）任务生效时间（Valid Time），任务生效时间是任务的等待时间，不占用工程师 的操作处理时间。每项任务各自的生效时间不相同。 （7）任务交货期(Due Date），如果任务到期不能完成会影响工程师的绩效考核，还会 85 降低顾客的满意度。 目前该部门分为 AA 和 DC 两组，AA 组有 4 位工程师，DC 组有 5 位工程师，组内工 程师是并行的。工作时间为周一到周五 9:00-12:00 和 13:00-17:30。其目标为：（1）确保各 项服务按期完成，降低未按期完成的任务的数量；（2）提高顾客的满意率，降低任务的延 期时间；（3）均衡分配员工工作量，提高员工的满意度。 1.2 模型建立 90 通过对该部门的现有状况和各项约束的分析，为了完善模型，在原有 AA、DC 组的基 础上，增加两个虚拟组 AA’、DC’组来处理任务在每个组所需要的生效时间（Valid Time）， 虚拟组可同时处理无穷多的任务，而任务的流程是不同的，如图 3 所示。 图 3 加入虚拟组后的任务流程图（注：节点 1’、2’为任务的生效时间处理过程） Fig.3 Task Flow with Virtual Groups（1’, 2’ Process of Task’s Valid time） 由于任务经过每个组的顺序不同，所以该调度问题属于 4 个柔性工作车间（Flexible Job Shop）[15]调度问题，同时又有优先级 prio、不可中断（非抢占，Non-preemptive）、异任务 流程 prec、到达时间 rj、处理时间 pj、交货期 dj 不同，其调度目标为最小化总延迟时间 Dj、 95 100 - 3 -
    中国科技论文在线 http://www.paper.edu.cn 最小化总完工时间 Cj、最小化时间表长 Cmax。综上所述，该调度问题如公式 1-3 所示： FJ 4 | prio non , − j , , preem prec r p d , , j j D max(0, = j C max max( ∑ | min C d ∑ − s ij D ) j p j j = 1, ⎧ = ⎨ 0, ⎩ 其它 ,min ∑ C ,min C max , j j （2） j = 1,2,..., n （1） ), i = 1,2,..., m * j 如果任务 由工程师 处理 i （3） s ij 105 2 调度算法设计 2.1 调度规则分析 该调度问题属于 NP-Hard 问题，尚没有最优算法。根据已有的规则[16]，结合该调度问 题的约束条件，本研究设计相应的规则如表 1 所示。 110 表 1 该调度问题所采用的规则 Tab. 1 Scheduling Rules Adopted by the Problem 参考变量 prio优先级 prec同一订单内部任务的先后顺序 rj任务到达时间 pj任务处理时间 vj 任务生效时间 dj 任务交货期 fj 订单总流程量 调度规则 按照订单的priority（1，2，3)递增 —— FCFS SPT或LPT 递减V-或递增V+ EDD 递减 F-或递增 F+ tj工程师处理任务累计时间 根据参考变量性质不同，相应的调度规则分为以下几类： （1） 关键调度规则：必须满足的约束对应的规则，根据这些规则确定关键调度规则集 SQT：首先分配给tj小的工程师，均衡工程师任务量 115 合{prec，prio}； （2） 任务约束规则：如对应于任务到达时间 rj、任务处理时间 pj、任务生效时间 vj、 任务总流程量 fj 等的调度规则 FCFS、SPT 与 LPT、V-与 V+、F-与 F+等规则； （3） 评价调度规则：如对应于任务交货期 dj、工程师累计时间 tj 的调度规则 EDD、 SQT 等规则。 2.2 调度规则的加权组合 120 2.2.1 规则权重计算方法 定义某一参考变量的调度规则为 ri (i =1，2…,m)，目标为 oj (j =1,2…,l），规则 ri 对目 标 oj 影响因子为 aij，如公式 4 所示： a 11 a 21 ... a l 1 ⎡ ⎢ ⎢ ⎢ ⎢ ⎣ A = 125 则每种规则的权重如公式 5 所示： （4） m a 1 a m 2 ... a lm l m × ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ a 12 a 22 ... a l 2 ... ... a ij ... - 4 -
    中国科技论文在线 λ a i • m = ∑ j 1 = a ij l 由于该调度问题为最小化问题，权重 iaλ • 2.2.2 调度算法的构建 http://www.paper.edu.cn （5） a ij ∑ 越小说明规则的性能越好。 1 = i 130 依据上述权重计算方法进行选择与组合，依据规则权重对任务进行排序，步骤如下： （1） 如果同一参考变量有两种或者两种以上规则，如参考数据 pj，有 SPT 或 LPT 两 种规则，则需要利用规则权重计算方法计算各规则权重，选择权重小的规则作为该参考变量 的调度规则。形成参考变量与调度规则之间的单一映射集合。 （2） 确定关键调度规则集合内规则的先后顺序，首先应满足的是 prec 规则，其次是 prio 规则。 135 （3） 确定规则权值，对任务约束规则以及评价调度规则，则利用公式 4、5 计算各规 则的权重值λ，然后利用权重值λ对任务参考变量度量值 d 进行修正 'd dλ= × 。 （4） 确定任务的修正度量值 di，其计算方法如公式 6 所示： 140 145 150 155 i 1 d i 2 + × d d i = × λ 2 λ 1 d × 其中，n 为步骤三中需要修正的参考变量的个数。 （5）依据 id 递增得到任务的优化排序。 利用图形仿真软件 Flexsim 建模得到各规则的不同目标下的目标值，然后利用 Excel 处 （6） ... + + λ n in 理数据得到最终的权重值。 3 仿真模型建立 在算法研究的基础上，本文采用基于 C++的图形仿真软件 Flexsim[17]建立调度模型，如 图 4 所示。模型中使用 source 对象产生任务序列、queue 对象作为任务等待区、processor 对 象用于处理任务、sink 对象表示任务完成离开系统。通过 Flexsim 提供的表格数据导入 （Multiple Table Import）功能将 Excel 表格中的数据导入模型，模型所需数据如表 2 所示。 为了简化仿真模型，工程师的处理时间全部采用平均值，并假设上班时间内工程师一直处于 工作状态，其工作时间表由其 TimeTable 模块建立。 图 4 调度仿真模型 Fig4 Scheduling Simulation Model - 5 -
    中国科技论文在线 http://www.paper.edu.cn 表 2 仿真模型输入数据（由 IT 商务支持部门提供） Table 2 Input Data for Simulation Model Task Seq. AA-handle-time AA-valid-time DC-handle-time DC-valid-time Flow 1 1 2 3 … 15 9 30 … 1440 … 132 … 60 … Flow 2 DC … Total flow 2 1 1 … AA AA AA … 160 165 170 175 180 185 190 195 最后采用了 Flexsim 提供的编写代码模块进行了规则的创建： 首先，为任务实体设置标签以读取各种约束条件： setlabelnum(item,"priorityi",gettablenum("flowi",y,8)); setlabelnum(item,"aaprocesstime",gettablenum("flowi",y,1)); setlabelnum(item,"dcprocesstime",gettablenum("flowi",y,3)); setlabelnum(item,"flow1",gettablenum("flowi",y,5)); setlabelnum(item,"flow2",gettablenum("flowi",y,6)); setlabelnum(item,"aavalidtime",gettablenum("flowi",y,2)); setlabenum(item,"dcvalidtime",gettablenum("flowi",y,4)); 然后利用 Flexsim 的脚本语言 setrank()函数完成了任务的排序功能： int maxrank = 1; while(objectexists(curcompare) && getlabelnum(curcompare,labelname) <= curlabelnum/*&&objectexists(curcompare) && getlabelnum(curcompare,labelname1) <= curlabelnum1&&objectexists(curcompare) && getlabelnum(curcompare,labelname2) >= curlabelnum2&&objectexists(curcompare) && getlabelnum(curcompare,labelname3) <= curlabelnum3*/) //各参数比较 { maxrank++; curcompare = next(curcompare); } setrank(item,min(maxrank, content(current))); time()函数获得模型仿真中需要的时间参数： int x1=getlabelnum(item,"callid"); int x2=gettablenum("arrivetime",x1,1); double completetime=time()-x2;//总完工时间为各任务完工时间之和 settablenum("arrivetime",x1,2,complete); settablenum("arrivetime",x1,3,time()); 最后经过调试完成了仿真模型的建立。 4 仿真结果分析 本文利用该部门 196 天中的 25685 项任务对所提出的调度算法进行了验证与分析。选取 总完工时间、任务在 AA、DC 组总等待时间以及延期任务数为评价指标，设计了该调度算 法，首先，对同一参考变量的规则进行优选，参考变量 pj、vj、fj 从两种备用规则中分别选 择了 SPT，V+，F-规则；其次，确定了规则集{SPT，V+，F-，EDD, FCFS，SQT}的权重 {0.14,0.11,0.11,0.20,0.18,0.26}。最后，比较该部门现有调度方案（随机调度）、规则简单组 合方案与规则加权组合方案。表 3 中原有资源配置方案下的数据表明：规则加权组合的方案 明显优于规则简单组合和没有采用调度规则的方案。 - 6 -
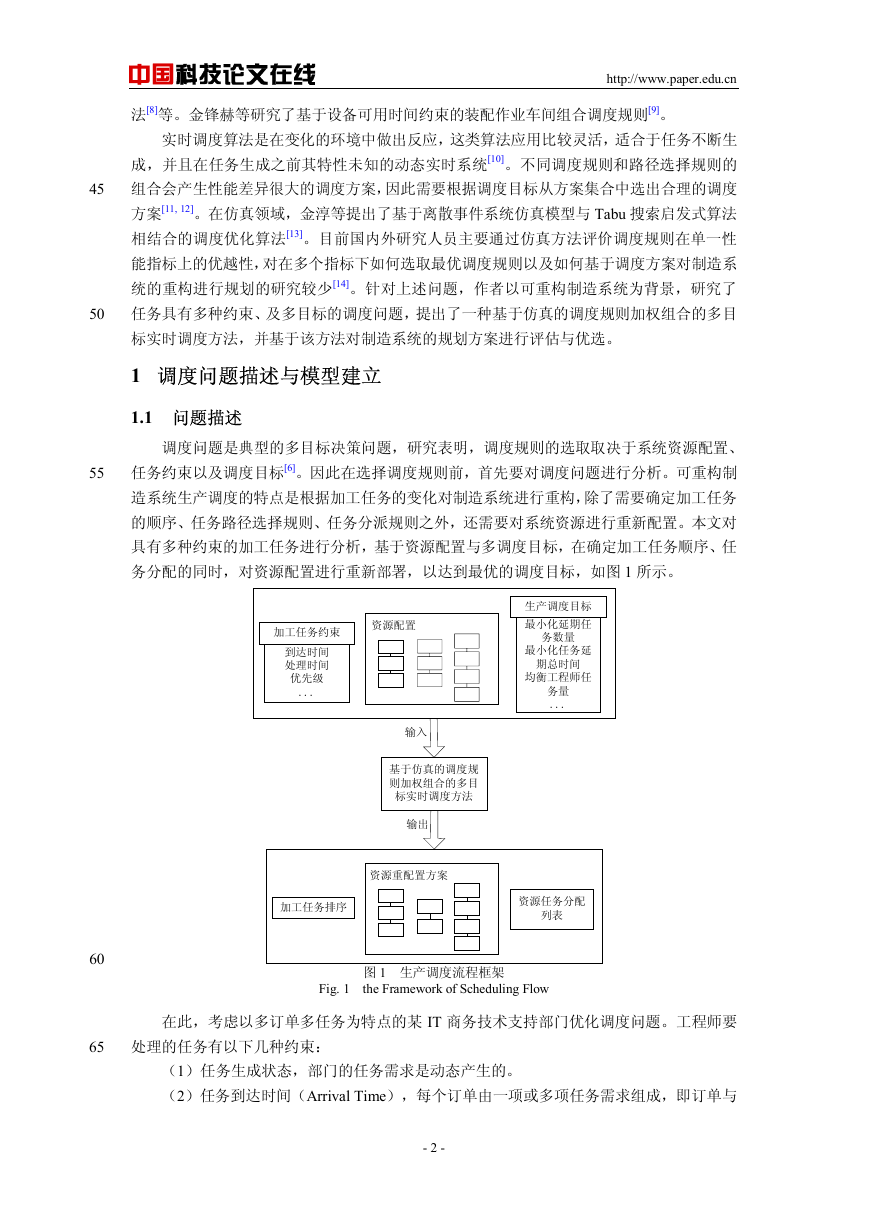
    中国科技论文在线 http://www.paper.edu.cn 表 3 不同调度方案的仿真结果 Tab. 3 Simulation Results for Different Scheduling Schemes 任务在 DC 组总 等待时间/天 任务在 AA 组总 等待时间/天 原有资源 配置方案 资源重配 置方案1 资源重配 置方案2 现有状况 规则简单组合 规则加权组合 现有状况 规则简单组合 规则加权组合 /天 调度方案 总完工时间 168078 166717 166577 166450 164123 193751 167001 166553 166290 现有状况 规则简单组合 规则加权组合 382 245 210 14320 13956 13021 142795 141324 140263 163395 162098 161165 147829 145793 145528 19905 20855 20825 延期任务 数 6152 4320 983 4108 2320 65 6104 4369 1043 延期任务 率（%） 23.9 16.8 3.8 15.9 9.0 0.2 23.7 17.0 4.0 AA组 DC组 AA组 DC组 AA组 DC组 （a）原有资源配置方案 （b）资源重配置方案1 200 205 210 图 5 资源配置方案及其重配置方案 Fig. 5 Resource Configuration/Reconfiguration Schemes （c）资源重配置方案2 在原有资源配置方案下，即 AA 组 4 名工程师，DC 组 5 名工程师（如图 5a 所示），采 取调度规则加权组合方案时各组中工程师的利用率趋于相等，方案达到了均衡工程师任务 量，提高职工满意率的目标，如图 5a 所示。同时不难发现，当采取最优方案时，仍有部分 的任务延期，而且 AA 组工程师的利用率均在 0.50 以下，利用率很低，DC 组工程师的利用 率都接近于 0.90，利用率很高，由此可知此部门人员分配不合理，DC 组为此部门的瓶颈。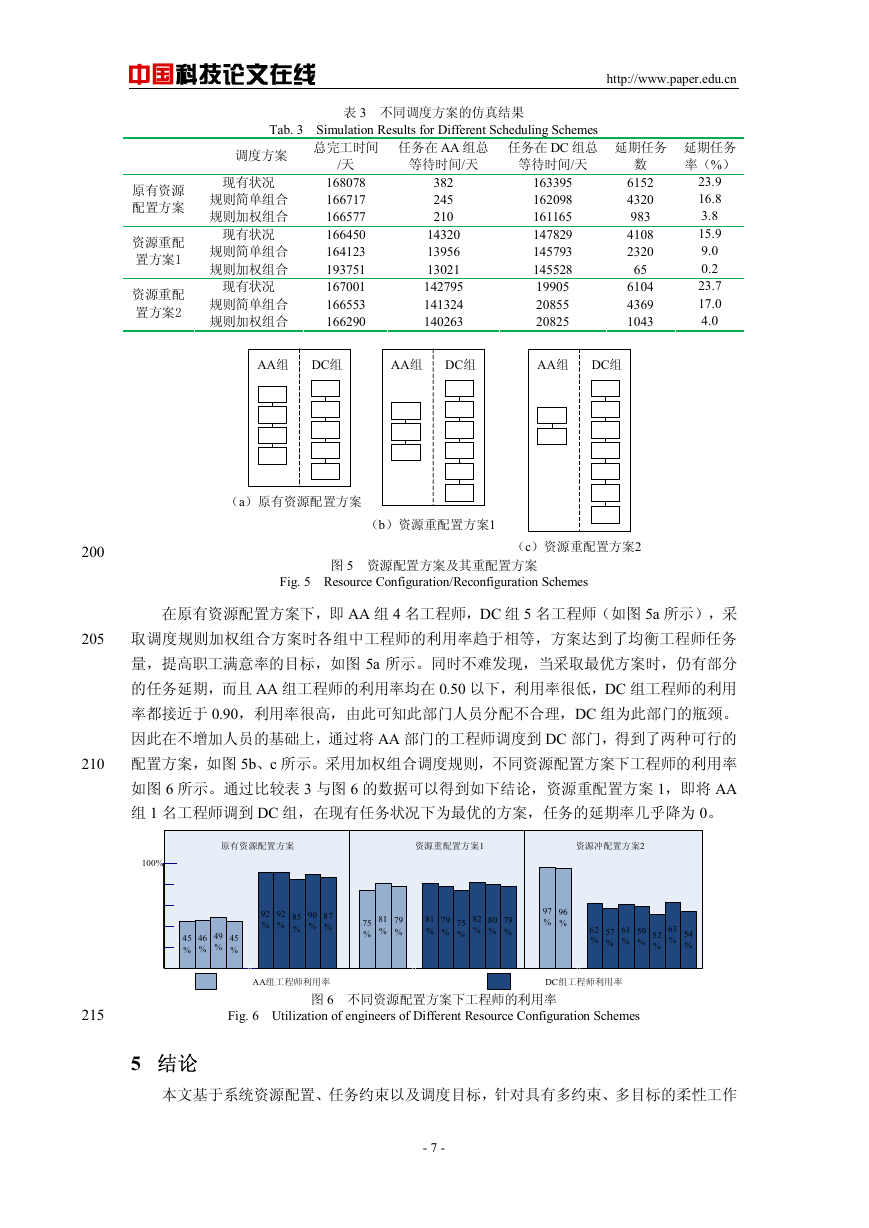 因此在不增加人员的基础上，通过将 AA 部门的工程师调度到 DC 部门，得到了两种可行的 配置方案，如图 5b、c 所示。采用加权组合调度规则，不同资源配置方案下工程师的利用率 如图 6 所示。通过比较表 3 与图 6 的数据可以得到如下结论，资源重配置方案 1，即将 AA 组 1 名工程师调到 DC 组，在现有任务状况下为最优的方案，任务的延期率几乎降为 0。 原有资源配置方案 资源重配置方案1 资源冲配置方案2 100% 92 % 92 % 85 % 90 % 87 % 75 % 81 % 79 % 81 % 79 % 75 % 82 % 80 % 79 % 97 % 96 % 62 % 57 % 61 % 59 % 63 % 54 % 52 % 45 % 46 % 49 % 45 % 0 AA组工程师利用率 0 0 DC组工程师利用率 图 6 不同资源配置方案下工程师的利用率 Fig. 6 Utilization of engineers of Different Resource Configuration Schemes 215 5 结论 本文基于系统资源配置、任务约束以及调度目标，针对具有多约束、多目标的柔性工作 - 7 -
    中国科技论文在线 http://www.paper.edu.cn 可重构车间系统，设计了基于多种调度规则加权组合的多目标实时调度算法，即克服了传统 规则简单组合在解决多目标调度问题难以确定最优组合的缺点，又保持了规则调度算法的简 单易行等特点。该算法已应用于某 IT 部门任务调度系统中，在均衡工程师工作量，降低延 期任务的数量的同时，对各部门的人员配置也起到了指导作用。 [参考文献] (References) [1] Koren Y, Heisel U, Jovane F, et al. Reconfigurable Manufacturing Systems[J]. Annals of the CIRP. 1999, 48(2): 527-540. [2] Elmaraghy H. Flexible and reconfigurable manufacturing systems paradigms[J]. International Journal of Flexible Manufacturing Systems. 2005, 17(4): 261-276. [3] Elmaraghy H. Reconfigurable Process Plans For Responsive Manufacturing Systems[J]. Digital Enterprise Tech-nology. 2007: 35-44. [4] Youssef A, Elmaraghy H A. Modeling and optimization of multiple-aspect RMS configurations[J]. International Journal of Production Research. 2006, 44(22): 4929-4958. [5] Schmidt G. Performance guarantee of two simple priority rules for production scheduling[J]. International Jour-nal of Production Economics. 2000, 68(2): 151-159. [6] An Z, Su C. Rule and Simulation-Based Parallel Machine Job-Shop Scheduling[J]. Industrial Engineering. 2010, 13(1): 5.(In Chinese) 安政，苏春. 基于规则和仿真的多机并行作业车间生产调度研究[J]. 工业工程. 2010, 13(1): 5. [7] He Y, Hui C. A rule-based genetic algorithm for the scheduling of single-stage multi-product batch plants with parallel units[J]. Computers & Chemical Engineering. 2008, 32(12): 3067-3083. [8] Jayamohan M S, Rajendran C. Development and analysis of cost-based dispatching rules for job shop schedul-ing[J]. European Journal of Operational Research. 2004, 157(2): 307-321. [9] Jin F, Kong F, Jin D, et al. Scheduling rules for assembly Job Shop based on machine available time[J]. Computer Integrated Manufacturing Systems. 2008, 14(9): 6.(In Chinese) 金锋赫，孔繁森，金东园，等. 基于 设备可用时间约束的装配作业车间调度规则[J]. 计算机集成制造系统. 2008, 14(9): 6. [10] Vinod V, Sridharan R. Simulation modeling and analysis of due-date assignment methods and scheduling deci-sion rules in a dynamic job shop production system[J]. International Journal of Production Economics. 2011, 129(1): 127-146. [11] Lacomme P, Moukrim A, Tchernev N. Simultaneous job input sequencing and vehicle dispatching in a single-vehicle automated guided vehicle system: a heuristic branch-and-bound approach coupled with a discrete events simulation model[Z]. 2005: 43, 1911-1942. [12] Zheng F, Sun S, Wu X. Selection of scheduling rules based on genetic algorithm and process simulation[J]. Computer Integrated Manufacturing Systems. 2004, 10(7): 7.(In Chinese) 郑锋，孙树栋，吴秀丽. 基于遗传算 法和模型仿真的调度规则决策方法[J]. 计算机集成制造系统. 2004, 10(7): 7. [13] Chun J, Yu Y, Zhao L, et al. Research on Optimal Scheduling on Gate Operation on Container Terminal Based on Simulation Optimization Method[J]. Journal of System Simulation. 2008, 20(8): 5.(In Chinese) Chun Jin，于越，赵璐，等. 基于仿真优化的集装箱港口大门作业调度研究[J]. 系统仿真学报. 2008, 20(8): 5. [14] Wang G, Ning R, Wang A, et al. Combination Decision Problem of Scheduling Rules Based on Simulation[J]. Transactions of Beijing Institute of Technology. 2006, 26(7): 598-601.(In Chinese) 王国新，宁汝新，王爱民， 等. 基于仿真的调度规则组合决策研究[J]. 北京理工大学学报. 2006, 26(7): 598-601. [15] Xia W, Wu Z. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling prob-lems[J]. Computers & Industrial Engineering. 2005, 48(2): 409-425. [16] Tang H, Zhao C. Scheduling Introduction [M]. Beijing: Science Press, 2005.(In Chinese) 唐恒永，赵传立. 排序引论[M]. 北京: 科学出版社, 2005. [17] Beaverstock M, Greenwood A, Lavery E, et al. Applied Simulation: Modeling and Analysis Using Flexsim Software Products, Inc., 2011. 220 225 230 235 240 245 250 255 260 265 - 8 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料