第1页 / 共33页
第2页 / 共33页
第3页 / 共33页
第4页 / 共33页
第5页 / 共33页
第6页 / 共33页
第7页 / 共33页
第8页 / 共33页
LSTM 算法 长短期记忆网络.pdf
2017/10/6
Exploring LSTMs
Exploring LSTMs
The first time I learned about LSTMs, my eyes glazed over.
Not in a good, jelly donut kind of way.
It turns out LSTMs are a fairly simple extension to neural networks, and they're behind
a lot of the amazing achievements deep learning has made in the past few years. So
I'll try to present them as intuitively as possible – in such a way that you could have
discovered them yourself.
But first, a picture:
Aren't LSTMs beautiful? Let's go.
(Note: if you're already familiar with neural networks and LSTMs, skip to the middle –
the first half of this post is a tutorial.)
Neural Networks
Imagine we have a sequence of images from a movie, and we want to label each
image with an activity (is this a fight?, are the characters talking?, are the characters
eating?).
How do we do this?
One way is to ignore the sequential nature of the images, and build a per-image
classifier that considers each image in isolation. For example, given enough images
and labels:
Our algorithm might first learn to detect low-level patterns like shapes and edges.
With more data, it might learn to combine these patterns into more complex ones, like
faces (two circular things atop a triangular thing atop an oval thing) or cats.
And with even more data, it might learn to map these higher-level patterns into activities
themselves (scenes with mouths, steaks, and forks are probably about eating).
http://blog.echen.me/2017/05/30/exploring-lstms/
1/33
2017/10/6
Exploring LSTMs
This, then, is a deep neural network: it takes an image input, returns an activity
output, and – just as we might learn to detect patterns in puppy behavior without
knowing anything about dogs (after seeing enough corgis, we discover common
characteristics like fluffy butts and drumstick legs; next, we learn advanced features
like splooting) – in between it learns to represent images through hidden layers of
representations.
Mathematically
I assume people are familiar with basic neural networks already, but let's quickly
review them.
A neural network with a single hidden layer takes as input a vector x, which we can
think of as a set of neurons.
Each input neuron is connected to a hidden layer of neurons via a set of learned weights.
The jth hidden neuron outputs
The hidden layer is fully connected to an output layer, and the jth output neuron outputs
. If we need probabilities, we can transform the output layer via a softmax
is an activation function.
, where
function.
In matrix notation:
where
x is our input vector
W is a weight matrix connecting the input and hidden layers
V is a weight matrix connecting the hidden and output layers
Common activation functions for
are the sigmoid function,
numbers into the range (0, 1); the hyperbolic tangent,
into the range (-1, 1), and the rectified linear unit,
Here's a pictorial view:
, which squashes
, which squashes numbers
.
http://blog.echen.me/2017/05/30/exploring-lstms/
2/33
=
ϕ
(
)
h
j
∑
i
w
i
j
x
i
ϕ
=
y
j
∑
i
v
i
j
h
i
h
=
ϕ
(
W
x
)
y
=
V
h
ϕ
σ
(
x
)
t
a
n
h
(
x
)
R
e
L
U
(
x
)
=
m
a
x
(
0
,
x
)
2017/10/6
Exploring LSTMs
(Note: to make the notation a little cleaner, I assume x and h each contain an extra
bias neuron fixed at 1 for learning bias weights.)
Remembering Information with RNNs
Ignoring the sequential aspect of the movie images is pretty ML 101, though. If we
see a scene of a beach, we should boost beach activities in future frames: an image
of someone in the water should probably be labeled swimming, not bathing, and an
image of someone lying with their eyes closed is probably suntanning. If we
remember that Bob just arrived at a supermarket, then even without any distinctive
supermarket features, an image of Bob holding a slab of bacon should probably be
categorized as shopping instead of cooking.
So what we'd like is to let our model track the state of the world:
1. After seeing each image, the model outputs a label and also updates the
knowledge it's been learning. For example, the model might learn to automatically
discover and track information like location (are scenes currently in a house or beach?),
time of day (if a scene contains an image of the moon, the model should remember that
it's nighttime), and within-movie progress (is this image the first frame or the 100th?).
Importantly, just as a neural network automatically discovers hidden patterns like edges,
shapes, and faces without being fed them, our model should automatically discover useful
information by itself.
2. When given a new image, the model should incorporate the knowledge it's gathered
to do a better job.
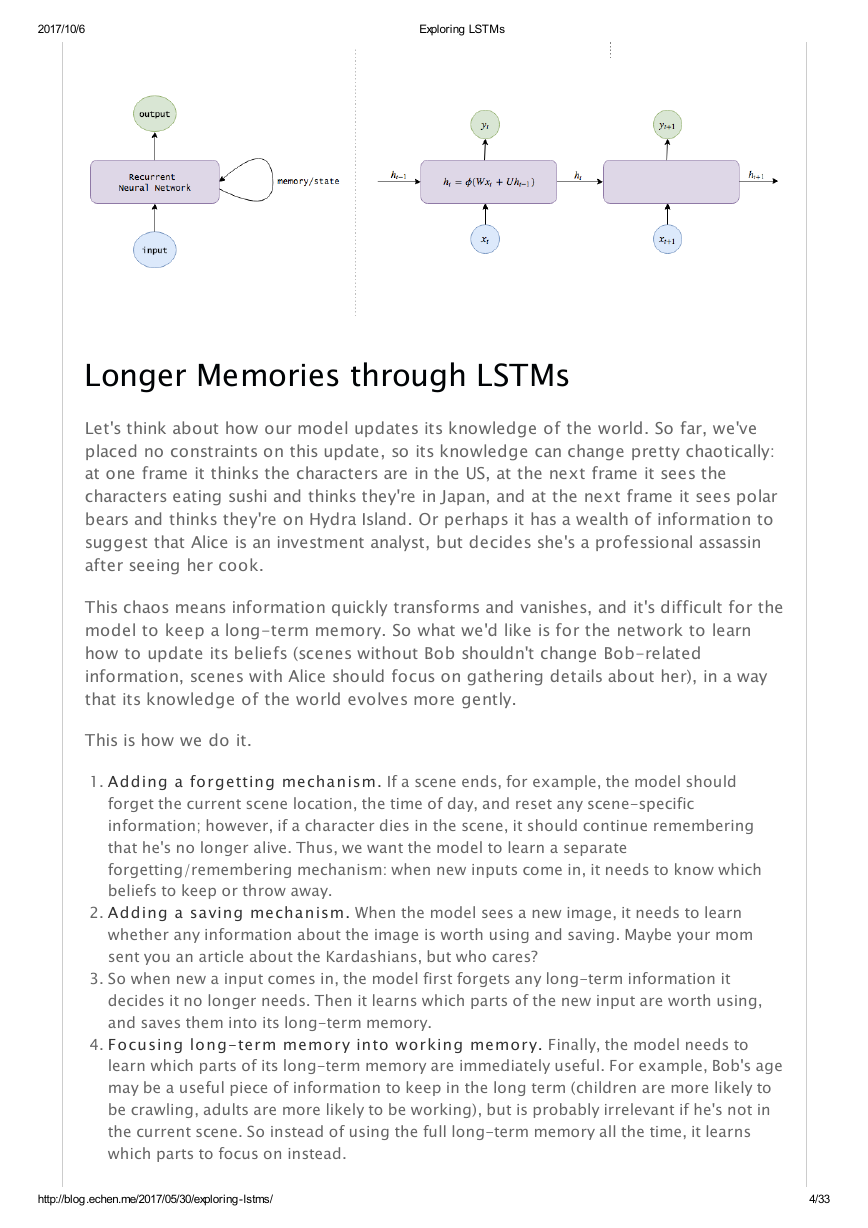
This, then, is a recurrent neural network. Instead of simply taking an image and
returning an activity, an RNN also maintains internal memories about the world
(weights assigned to different pieces of information) to help perform its
classifications.
Mathematically
So let's add the notion of internal knowledge to our equations, which we can think
of as pieces of information that the network maintains over time.
But this is easy: we know that the hidden layers of neural networks already encode
useful information about their inputs, so why not use these layers as the memory
passed from one time step to the next? This gives us our RNN equations:
Note that the hidden state computed at time (
, our internal knowledge) is fed
back at the next time step. (Also, I'll use concepts like hidden state, knowledge,
memories, and beliefs to describe
interchangeably.)
http://blog.echen.me/2017/05/30/exploring-lstms/
3/33
=
ϕ
(
W
+
U
)
h
t
x
t
h
t
−
1
=
V
y
t
h
t
t
h
t
h
t
2017/10/6
Exploring LSTMs
Longer Memories through LSTMs
Let's think about how our model updates its knowledge of the world. So far, we've
placed no constraints on this update, so its knowledge can change pretty chaotically:
at one frame it thinks the characters are in the US, at the next frame it sees the
characters eating sushi and thinks they're in Japan, and at the next frame it sees polar
bears and thinks they're on Hydra Island. Or perhaps it has a wealth of information to
suggest that Alice is an investment analyst, but decides she's a professional assassin
after seeing her cook.
This chaos means information quickly transforms and vanishes, and it's difficult for the
model to keep a long-term memory. So what we'd like is for the network to learn
how to update its beliefs (scenes without Bob shouldn't change Bob-related
information, scenes with Alice should focus on gathering details about her), in a way
that its knowledge of the world evolves more gently.
This is how we do it.
1. Adding a forgetting mechanism. If a scene ends, for example, the model should
forget the current scene location, the time of day, and reset any scene-specific
information; however, if a character dies in the scene, it should continue remembering
that he's no longer alive. Thus, we want the model to learn a separate
forgetting/remembering mechanism: when new inputs come in, it needs to know which
beliefs to keep or throw away.
2. Adding a saving mechanism. When the model sees a new image, it needs to learn
whether any information about the image is worth using and saving. Maybe your mom
sent you an article about the Kardashians, but who cares?
3. So when new a input comes in, the model first forgets any long-term information it
decides it no longer needs. Then it learns which parts of the new input are worth using,
and saves them into its long-term memory.
4. Focusing long-term memory into working memory. Finally, the model needs to
learn which parts of its long-term memory are immediately useful. For example, Bob's age
may be a useful piece of information to keep in the long term (children are more likely to
be crawling, adults are more likely to be working), but is probably irrelevant if he's not in
the current scene. So instead of using the full long-term memory all the time, it learns
which parts to focus on instead.
http://blog.echen.me/2017/05/30/exploring-lstms/
4/33
2017/10/6
Exploring LSTMs
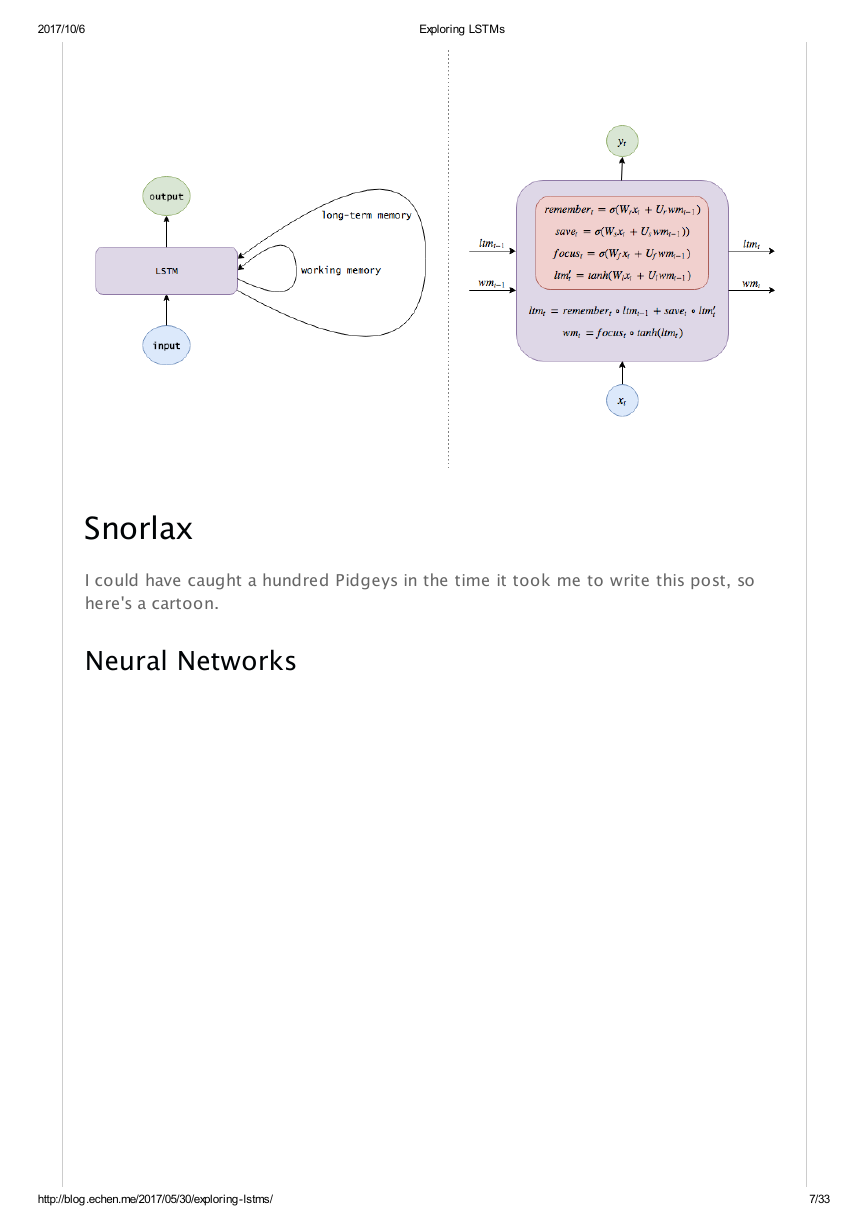
This, then, is an long short-term memory network. Whereas an RNN can overwrite
its memory at each time step in a fairly uncontrolled fashion, an LSTM transforms its
memory in a very precise way: by using specific learning mechanisms for which pieces
of information to remember, which to update, and which to pay attention to. This
helps it keep track of information over longer periods of time.
Mathematically
Let's describe the LSTM additions mathematically.
At time , we receive a new input
memories passed on from the previous time step,
vectors), which we want to update.
. We also have our long-term and working
and
(both n-length
We'll start with our long-term memory. First, we need to know which pieces of
long-term memory to continue remembering and which to discard, so we want to
use the new input and our working memory to learn a remember gate of n numbers
between 0 and 1, each of which determines how much of a long-term memory
element to keep. (A 1 means to keep it, a 0 means to forget it entirely.)
Naturally, we can use a small neural network to learn this remember gate:
(Notice the similarity to our previous network equations; this is just a shallow neural
network. Also, we use a sigmoid activation because we need numbers between 0 and
1.)
Next, we need to compute the information we can learn from
addition to our long-term memory:
, i.e., a candidate
is an activation function, commonly chosen to be
.
Before we add the candidate into our memory, though, we want to learn which
parts of it are actually worth using and saving:
(Think of what happens when you read something on the web. While a news article
might contain information about Hillary, you should ignore it if the source is
Breitbart.)
Let's now combine all these steps. After forgetting memories we don't think we'll ever
need again and saving useful pieces of incoming information, we have our updated
long-term memory:
where denotes element-wise multiplication.
http://blog.echen.me/2017/05/30/exploring-lstms/
5/33
t
x
t
l
t
m
t
−
1
w
m
t
−
1
r
e
m
e
m
b
e
=
σ
(
+
w
)
r
t
W
r
x
t
U
r
m
t
−
1
x
t
l
t
=
ϕ
(
+
w
)
m
′
t
W
l
x
t
U
l
m
t
−
1
ϕ
t
a
n
h
s
a
v
=
σ
(
+
w
)
e
t
W
s
x
t
U
s
m
t
−
1
l
t
=
r
e
m
e
m
b
e
∘
l
t
+
s
a
v
∘
l
t
m
t
r
t
m
t
−
1
e
t
m
′
t
∘
2017/10/6
Exploring LSTMs
Next, let's update our working memory. We want to learn how to focus our
long-term memory into information that will be immediately useful. (Put differently,
we want to learn what to move from an external hard drive onto our working laptop.)
So we learn a focus/attention vector:
Our working memory is then
In other words, we pay full attention to elements where the focus is 1, and ignore
elements where the focus is 0.
And we're done! Hopefully this made it into your long-term memory as well.
To summarize, whereas a vanilla RNN uses one equation to update its hidden
state/memory:
An LSTM uses several:
where each memory/attention sub-mechanism is just a mini brain of its own:
(Note: the terminology and variable names I've been using are different from the
usual literature. Here are the standard names, which I'll use interchangeably from now
on:
, is usually called the cell state, denoted
. This is
.
, is usually called the hidden state, denoted
The long-term memory,
The working memory,
analogous to the hidden state in vanilla RNNs.
The remember vector,
that a 1 in the forget gate still means to keep the memory and a 0 still means to forget it),
denoted
The save vector,
the input to let into the cell state), denoted
The focus vector,
, is usually called the input gate (as it determines how much of
, is usually called the forget gate (despite the fact
, is usually called the output gate, denoted
. )
.
.
http://blog.echen.me/2017/05/30/exploring-lstms/
6/33
f
o
c
u
=
σ
(
+
w
)
s
t
W
f
x
t
U
f
m
t
−
1
w
=
f
o
c
u
∘
ϕ
(
l
t
)
m
t
s
t
m
t
=
ϕ
(
W
+
U
)
h
t
x
t
h
t
−
1
l
t
=
r
e
m
e
m
b
e
∘
l
t
+
s
a
v
∘
l
t
m
t
r
t
m
t
−
1
e
t
m
′
t
w
=
f
o
c
u
∘
t
a
n
h
(
l
t
)
m
t
s
t
m
t
r
e
m
e
m
b
e
=
σ
(
+
w
)
r
t
W
r
x
t
U
r
m
t
−
1
s
a
v
=
σ
(
+
w
)
e
t
W
s
x
t
U
s
m
t
−
1
f
o
c
u
=
σ
(
+
w
)
s
t
W
f
x
t
U
f
m
t
−
1
l
t
=
t
a
n
h
(
+
w
)
m
′
t
W
l
x
t
U
l
m
t
−
1
l
t
m
t
c
t
w
m
t
h
t
r
e
m
e
m
b
e
r
t
f
t
s
a
v
e
t
i
t
f
o
c
u
s
t
o
t
2017/10/6
Exploring LSTMs
Snorlax
I could have caught a hundred Pidgeys in the time it took me to write this post, so
here's a cartoon.
Neural Networks
http://blog.echen.me/2017/05/30/exploring-lstms/
7/33
2017/10/6
Exploring LSTMs
Recurrent Neural Networks
LSTMs
http://blog.echen.me/2017/05/30/exploring-lstms/
8/33
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
