2011年福建省宁德市中考数学真题及答案.doc-资料库

第1页 / 共10页

第2页 / 共10页

第3页 / 共10页

第4页 / 共10页

第5页 / 共10页

第6页 / 共10页

第7页 / 共10页

第8页 / 共10页

2011 年福建省宁德市中考数学真题及答案（满分 150 分；考试时间 120 分钟）友情提示：所有答案都必须填涂在答题卡上，在本试卷上作答无效．一、选择题（本大题有 10 小题，每小题 4 分，满分 40 分.每小题只有一个正确的选项，请用 2B 铅笔在答题卡的相应位置填涂） 1.下列各数中，最小的数是（）. A. 1 2 B.0 C.－1 D.－3 2.下列运算正确的是（）． A. a  2 a  3 a B. 2 aa   3 a C. 6 a 2  a  3 a  D. 3 a  2 2 6 a 3.如图，装修工人向墙上钉木条.若∠2＝110°，要使木条 b 与 a 平行，则∠1 的度数等于（）. A．55º B．70º C．90º D．110º 4.不等式 5＋2x＜1 的解集在数轴上表示正确的是（）. 2 1） a b 第 3 题图 -2 A. 0 -2 0 B. 0 -2 C. 0 D. 3 5.下列图标中，属于中心对称的是（）. A. B. C. D. 6.“ a 是实数， a  1 2  0 ”这一事件是（）. A.必然事件 B.不确定事件 C.不可能事件 D.随机事件 7.如图所示几何体的俯视图是（）. A. B. C. D. 第 7 题图

8.如图，要围一个面积为 20 的矩形，若矩形的两邻边分别为 x  2  x 10 、 y ，则 y 与 x 的函数图象大致是（ y 10 y 10 ）. 2 O 2 10 x A． 2 O 2 10 x B． y 10 2 O y 10 2 O 2 10 x C． 2 10 x D． A y x 9.将量角器按如图所示的方式放置在三角形纸片上，使点 C在半圆圆心上，点 B在半圆上，则∠A的度数约为（）. A．10° B．20° C．25° D．35° 10.已知： a 1  x 1 (x≠0 且 x≠－1)， a 2  ）（ 1 ， a 1 1 a 3 1 1  ）（ 2 a ，…， B C 第 9 题图 a n a  1n 1 （ 1 ，则 2011a 等于( ） )． A.x B. x＋1 C. 1 x D. x 1x 二、填空题（本大题有 8 小题，每小题 3 分，满分 24 分．请将答案用黑色签字笔填入答题卡的相应位置） 11.化简： x  1 x  1   2 x ＝______. 12.分解因式： a 2  ＝________. 3 a 13.如图，人民币旧版壹角硬币内部的正多边形每个内角度数是____°. 14.函数 y  3  2 x ，当 x＝3 时，y＝_______. 15.如图，AB 是半圆 O 的直径，OD⊥AC，OD=2，则弦 BC 的长为_______. 16.如图，在平面直角坐标系中，将△ABC 绕 A 点逆时针旋转 90°后，B 点对应点的坐标为________. 第 13 题图 C D O 第 15 题图 C B B 1 2 A 4 5 x 第 16 题图 A y 5 4 3 2 1 O 17.甲、乙俩射击运动员进行 10 次射击，甲的成绩是 7，7，8，9，8，9，10，9，9，9，乙的成绩

如图所示.则甲、乙射击成绩的方差之间关系是 2S 甲 2S ______ 乙 (填“＜”，“＝”，“＞”)．环 10 9 8 7 1 18.如图，△ABC 中，∠ACB＝90°，∠A＝30°,将△ABC 绕 C 2 3 6 5 4 第 17 题图 7 8 9 10- 次点按逆时针方向旋转α角（0°＜α＜90°）得到△DEC，设 CD 交 AB 于 F，连接 AD，当旋转角α度数为_______，△ADF 是等腰三角形。 E B C D F 30°（）α 第 18 题图 A 三、解答题（本大题有 8 小题，满分 86 分．请将解答过程用黑色签字笔写在答题卡的相应位置．作图或添辅助线用铅笔画完，再用黑色签字笔描黑） 19．（本题满分 14 分） ⑴计算：  3     14.3 0   12  1 ；    1 2    3   2  ⑵解方程： x 20．（本题满分 8 分） x 2 . 1 A D 已知：如图，点 E，C在线段 BF上， AB＝DE，AB∥DE，BE＝CF．求证：AC＝DF. B E C F 21．（本题满分 8 分）据《福建省第六次全国人口普查主要数据公报》显示，全省常住人口为 36894216 人.人口地区分布的数据如图 1.另外，我省区域面积分布情况如图 2. 800 600 400 200 0 福建省常住人口地区分布统计图人口/万人 712 481 353 278 256 250 265 福莆泉厦漳龙三南宁州田州门州岩明平德地区图 1 福建省区域面积分布统计图南平 2.62 三明 2.30 福州 1.22 宁德 1.34 龙岩 1.90 泉州 1.13 莆田 0.41 漳州 1.29 厦门 0.17 单位：万平方千米图 2

⑴全省常住人口用科学记数法表示为：___________人（保留四个有效数字）. ⑵若泉州人口占全省常住人口 22.03%，宁德占 7.64%，请补全图 1 统计图； ⑶全省九地市常住人口这组数据的中位数是_________万人； ⑷全省平均人口密度最大的是_______市，达_____人/平方千米. （平均人口密度＝常住人口数÷区域面积，结果精确到个位） 22．（本题满分 10 分）如图，均匀的正四面体的各面依次标有 1，2，3，4 四个数字.小明做了 60 次投掷试验，结果统计如下：朝下数字出现的次数 1 16 2 20 3 14 4 10 1 3 ⑴计算上述试验中“4 朝下”的频率是__________； ⑵“根据试验结果，投掷一次正四面体，出现 2 朝下的概率是 1 3 .”的说法正确吗？为什么？ ⑶随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于 4 的概率． 23．（本题满分 10 分）某旅行社 2010 年 1～5 月份，接待前往以福鼎太姥山、屏南白水洋、福安白云山为主要景点的宁德世界地质公园的游客 5000 人.今年同期比去年增加 40%，其中外地游客增加 50%，本地游客增加 10%.求 2010 年 1～5 月份该旅行社接待外地游客和本地游客分别是多少人？ 24．（本题满分 10 分）图 1 是安装在斜屋面上的热水器，图 2 是安装该热水器的侧面示意图.已知，斜屋面的倾斜角为 25°，长为 2.1 米的真空管 AB 与水平线 AD 的夹角为 40°，安装热水器的铁架水平横管 BC 长 0.2 米，求 ⑴真空管上端 B 到 AD 的距离（结果精确到 0.01 米）； ⑵铁架垂直管 CE 的长（结果精确到 0.01 米）. B C E D 图 1 ）25° 图 2 A

25．（本题满分 13 分）定义：三边长和面积都是整数的三角形称为“整数三角形”. 数学学习小组的同学从 32 根等长的火柴棒（每根长度记为 1 个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动. 小亮用 12 根火柴棒，摆成如图所示的“整数三角形”；小颖分别用 24 根和 30 根火柴棒摆出直角“整数三角形”；小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”. ⑴请你画出小颖和小辉摆出的“整数三角形”的示意图； 4 5 3 ⑵你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由. ①摆出等边“整数三角形”； ② 摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”. 26．（本题满分 13 分）直线 y 6 x 与 x轴、y轴分别交于点 A、B，点 E从 B点，出发以每秒 1 个单位的速度沿线段 BO向 O点移动（与 B、O点不重合），过 E作 EF∥AB，交 x轴于 F.将四边形 ABEF沿 EF 折叠，得到四边形 DCEF，设点 E的运动时间为 t秒． ⑴①直线 y 6 x 与坐标轴交点坐标是 A（___，___），B（___，___）； ②画出 t＝2 时，四边形 ABEF沿 EF折叠后的图形（不写画法）； ⑵若 CD交 y轴于 H点，求证：四边形 DHEF为平行四边形；并求 t为何值时，四边形 DHEF 为菱形（计算结果不需化简）； ⑶设四边形 DCEF落在第一象限内的图形面积为 S，求 S关于 t的函数表达式，并求出 S的最大值． y 4 3 2 1 -3 -2 -1 O -1 -2 -3 -4 -5 -6 E B F A 1 2 3 4 5 6 7 x

参考答案： ⑴本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可参照本答案的评分标准的精神进行评分. ⑵对解答题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的立意，可酌情给分. ⑶解答右端所注分数表示考生正确作完该步应得的累加分数. ⑷评分只给整数分. 一、选择题：（本大题有 10 小题，每小题 4 分，满分 40 分） 1.D；2.B；3.A；4.C；5.C；6.A；7.D；8.C；9.C；10.B. 二、填空题：（本大题有 8 小题，每小题 3 分，满分 24 分） 11.－1；12.a(a－3)；13.140；14.－3；15.4；16.（0,2）；17.＜；18.40°，或 20°. 三、解答题：（本大题有 8 小题，满分 86 分） 19.（满分 14 分） ⑴解：原式＝ 3213   2 …………4 分＝1 3 .…………7 分 ⑵解：方程两边都乘以 x   x 2 1  ，得  3 x  1   2 x  2 .…………4 分解这个方程，得 x ＝7.…………6 分检验：将 x ＝7 代入最简公分母， 所以， x ＝7 是原方程的解．…………7 分  x  2  1  0 . x 20．（满分 8 分）证法一：∵AB∥DE， ∴∠B＝∠DEC.…………1 分 ∵BE＝CF， ∴BE＋EC＝CF＋EC.…………2 分即 BC＝EF. 又∵AB＝DE，∴△ABC≌△DEF.…………6 分 ∴AC＝DF.…………8 分证法二：连接 AD， ∵AB＝DE，AB∥DE， ∴四边形 ABED是平行四边形.…………2 分 ∴AD∥BE，AD＝BE.

∵BE＝CF，∴AD∥CF，AD＝CF. ∴四边形 ACFD是平行四边形.…………6 分 ∴AC＝DF.…………8 分 21.（满分 8 分）解：⑴用科学记数法表示全省常住人口：3.689×107 人.…………2 分 ⑵泉州人口 812 万人，宁德人口 282 万人；画统计图正确.…………4 分 ⑶中位数是 282 万人.……………6 分 ⑷全省平均人口密度最大的是厦门市，达 2076 人/平方千米.…………8 分 22．（满分 10 分）解：⑴“4 朝下”的频率： 10  ；…………2 分 60 1 6 ⑵这种说法是错误的．在 60 次试验中，“2 朝下”的频率为 1 3 并不能说明“2 朝下”这一事件发生的概率为 1 3 ．只有当试验的总次数很大时，事件发生的频率才会稳定在相应的事件发生的概率附近．…………5 分 ⑶随机投掷正四面体两次，所有可能出现的结果如下：第一次第二次 1 2 3 4 1 （1，1）（2，1）（3，1）（4，1） 2 （1，2）（2，2）（3，2）（4，2） 3 （1，3）（2，3）（3，3）（4，3） 4 （1，4）（2，4）（3，4）（4，4）总共有 16 种结果，每种结果出现的可能性相同，而两次朝下数字之和大于 4 的结果 …………8 分有 10 种.……9 分 ∴ P （朝下数字之和大于 ） 4 10 16  5 8 .…………10 分 23.（满分 10 分）解法一：设去年同期接待外地游客为 x人，本地游客为 y人.………1 分依题意，得 x y     %50 1   5000 ,   1 x  %10  y  5000 1  （ ………6 分 .%40 ）解得 x y      , 3750 1250 . ………9 分答：去年 1～5 月份该旅行社接待外地游客 3750 人，本地游客 1250 人.…10 分解法二:设去年同期接待外地游客为 x人，则本地游客为（5000－x）人.………2 分

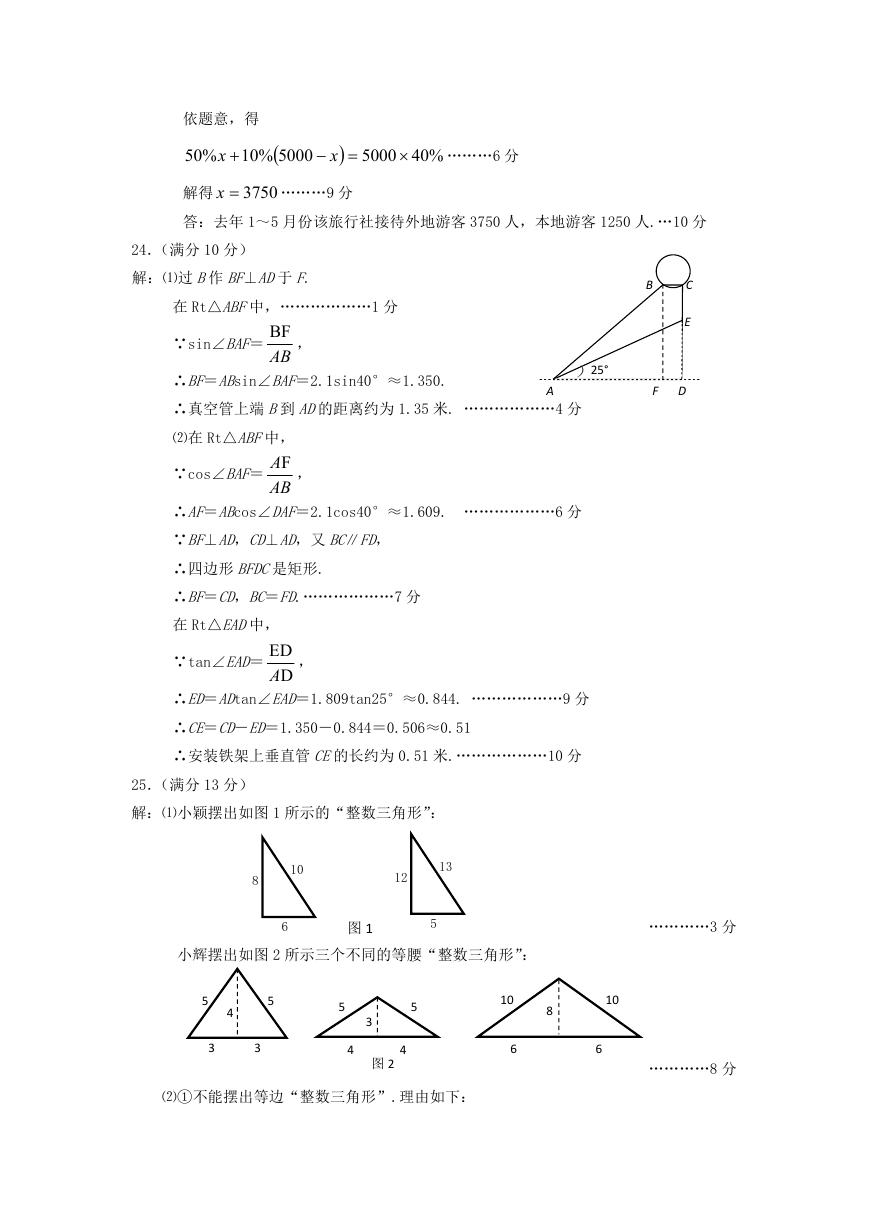
依题意，得 %50 x  %10  5000   x  5000  %40 ………6 分 x 解得 3750 答：去年 1～5 月份该旅行社接待外地游客 3750 人，本地游客 1250 人.…10 分 ………9 分 24．（满分 10 分）解：⑴过 B作 BF⊥AD于 F. 在 Rt△ABF中，………………1 分 ∵sin∠BAF＝ BF AB ， ∴BF＝ABsin∠BAF＝2.1sin40°≈1.350. B C E ）25° A F D ∴真空管上端 B到 AD的距离约为 1.35 米. ………………4 分 ⑵在 Rt△ABF中， AF AB ∵cos∠BAF＝， ∴AF＝ABcos∠DAF＝2.1cos40°≈1.609. ………………6 分 ∵BF⊥AD，CD⊥AD，又 BC∥FD， ∴四边形 BFDC是矩形. ∴BF＝CD，BC＝FD.………………7 分在 Rt△EAD中， ∵tan∠EAD＝ ED D A ， ∴ED＝ADtan∠EAD＝1.809tan25°≈0.844. ………………9 分 ∴CE＝CD－ED＝1.350－0.844＝0.506≈0.51 ∴安装铁架上垂直管 CE的长约为 0.51 米.………………10 分 25．（满分 13 分）解：⑴小颖摆出如图 1 所示的“整数三角形”： 10 8 13 12 6 图 1 5 …………3 分小辉摆出如图 2 所示三个不同的等腰“整数三角形”： 4 5 3 5 3 5 3 5 4 4 图 2 8 10 6 10 6 …………8 分 ⑵①不能摆出等边“整数三角形”.理由如下：

资料库

2011年福建省宁德市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料