第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
基于双闭环PID控制的一阶倒立摆控制系统设计.doc
基于双闭环PID控制的一阶倒立摆控制系统设计
自动控制原理课程设计
基于双闭环 PID 控制的一阶倒立摆控制系统设计
一、设计目的
倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型
例子。设计一个倒立摆的控制系统，使倒立摆这样一个不稳定的被控对象通过引
入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
二、设计要求
倒立摆的设计要求是使摆杆尽快地达到一个平衡位置，并且使之没有
大的振荡和过大的角度和速度。当摆杆到达期望的位置后，系统能克服随
机扰动而保持稳定的位置。实验参数自己选定，但要合理符合实际情况，控制
方式为双 PID 控制，并利用 MATLAB 进行仿真，并用 simulink 对相应的模块进
行仿真。
三、设计原理
倒立摆控制系统的工作原理是：由轴角编码器测得小车的位置和摆杆相对
垂直方向的角度，作为系统的两个输出量被反馈至控制计算机。计算机根据一定
的控制算法，计算出空置量，并转化为相应的电压信号提供给驱动电路，以驱动
直流力矩电机的运动，从而通过牵引机构带动小车的移动来控制摆杆和保持平
衡。
四、设计步骤
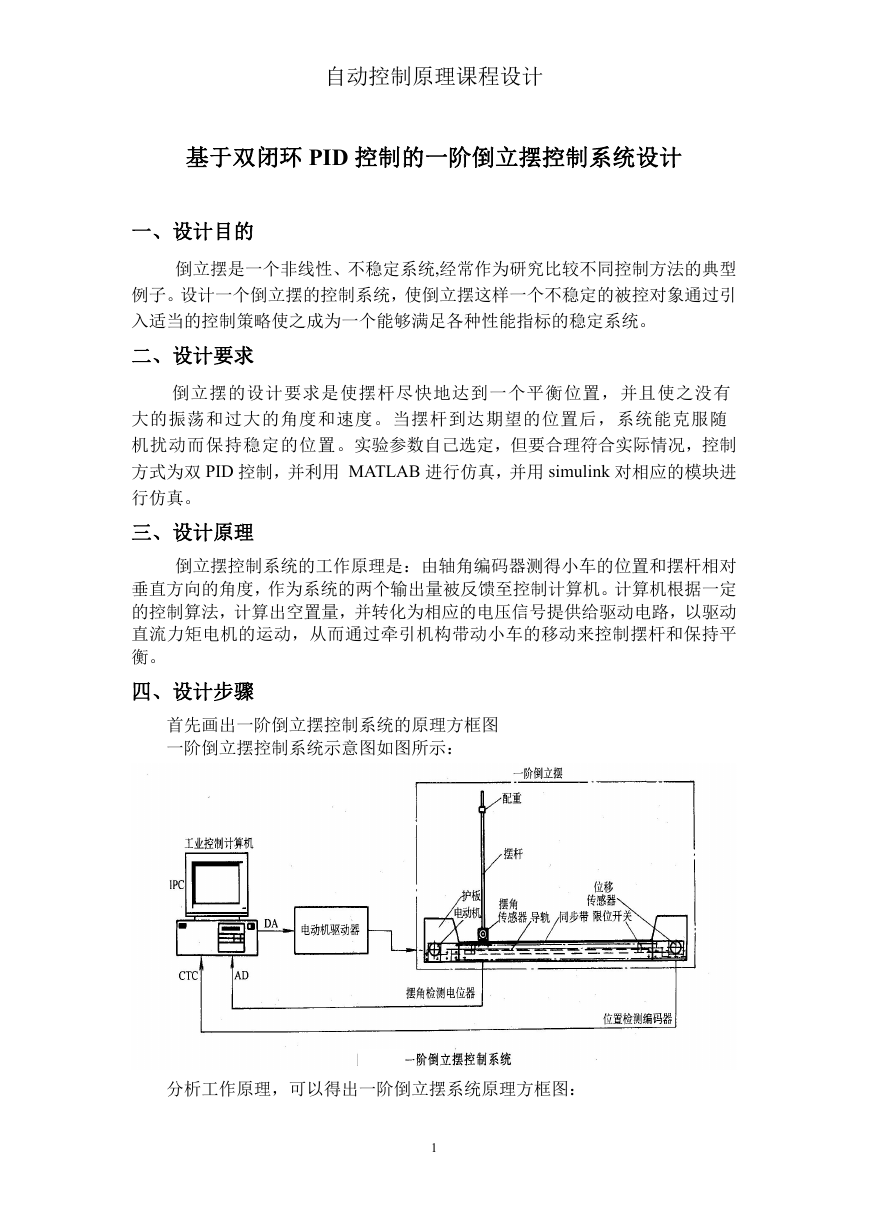
首先画出一阶倒立摆控制系统的原理方框图
一阶倒立摆控制系统示意图如图所示：
分析工作原理，可以得出一阶倒立摆系统原理方框图：
1
自动控制原理课程设计
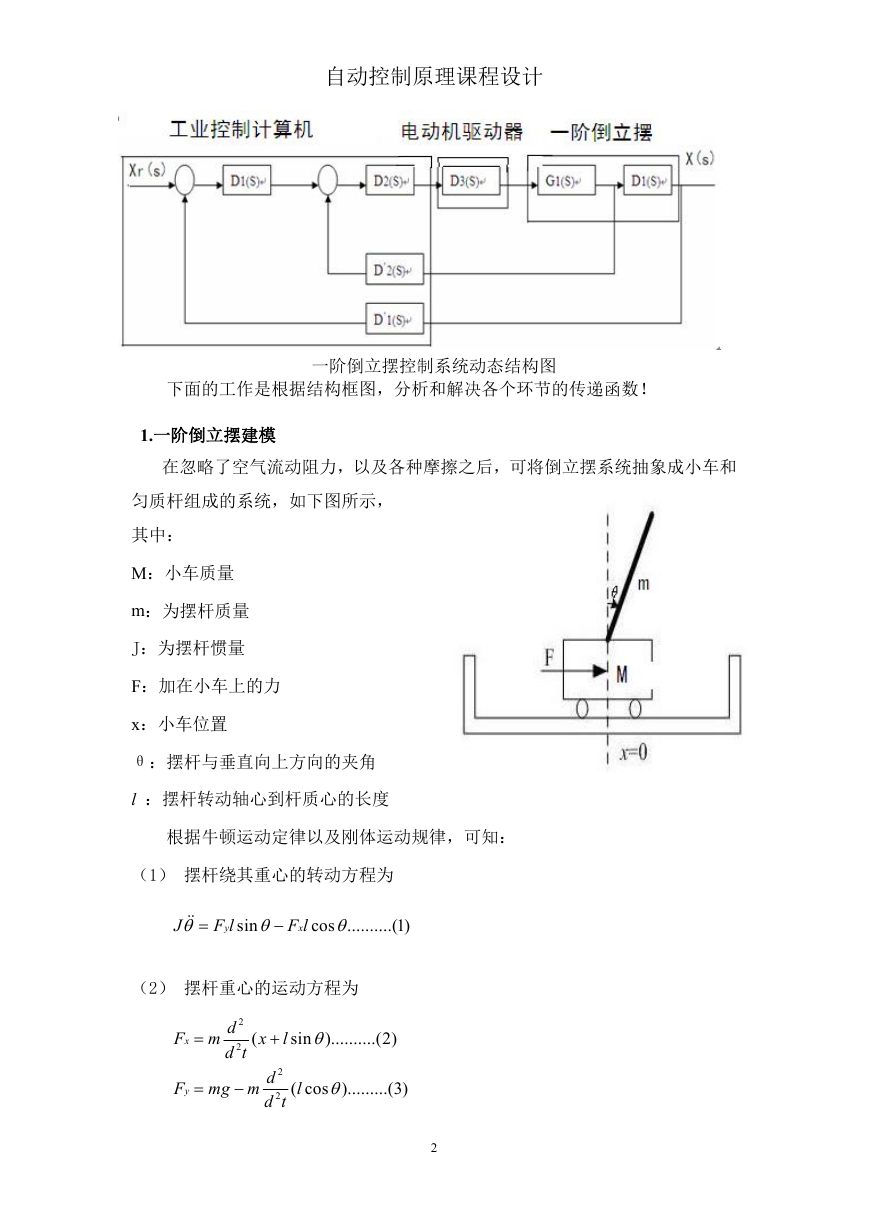
下面的工作是根据结构框图，分析和解决各个环节的传递函数！
一阶倒立摆控制系统动态结构图
1.一阶倒立摆建模
在忽略了空气流动阻力，以及各种摩擦之后，可将倒立摆系统抽象成小车和
匀质杆组成的系统，如下图所示，
其中：
M：小车质量
m：为摆杆质量
J：为摆杆惯量
F：加在小车上的力
x：小车位置
θ：摆杆与垂直向上方向的夹角
l ：摆杆转动轴心到杆质心的长度
根据牛顿运动定律以及刚体运动规律，可知：
（1） 摆杆绕其重心的转动方程为
J
F l
y
sin
F l
x
cos ..........(1)
（2） 摆杆重心的运动方程为
F m
x
2
d
2
d t
(
x
l
sin )..........(2)
F mg m
y
2
d
2
d t
( cos ).........(3)
l
2
自动控制原理课程设计
（3）小车水平方向上的运动为
F F M
x
2
d x
2
d t
..........(4)
联列上述 4 个方程，可以得出
一阶倒立精确气模型：
2
J ml F ml J ml
2
2
2
sin .
2 2
J ml M m m l
2 2
2
sin cos .
F m l
2 2
2
m l
2 2
m l g
2
cos
M m m
M m J ml
cos
2
sin cos
lgsin
x
ml
cos .
式中 J 为摆杆的转动惯量：
J
2ml
3
若只考虑θ在其工作点附近θ0=0 附近（
10
10
）的细微变化，则可
以近似认为：
2
sin
cos
0
1
..
x
..
(
(
2
)
J
(
mMJ
mmM
(
mMJ
22
glmFml
2
)
Mml
lg
)
Mml
mlF
2
)
若取小车质量 M=2kg,摆杆质量 m=1kg,摆杆长度 2 l =1m,重力加速度取
g=
10
/
sm
2
,则可以得
一阶倒立摆简化模型：
0.44
F
3.33
拉氏变换
..
x
..
0.4
F
12
( )
s
( )
F s
( )
x s
( )
s
2
0.4
12
s
2
1.1
s
s
2
10
即
G1(s)=
;
G2(s)=
一阶倒立摆环节问题解决！
2.电动机驱动器
选用日本松下电工 MSMA021 型小惯量交流伺服电动机，其有关参数如下：
3
自动控制原理课程设计
驱动电压：U=0~100V
额定功率：PN=200W
额定转速：n=3000r/min
转动惯量：J=3×10-6kg.m2
额定转矩：TN=0.64Nm
最大转矩：TM=1.91Nm
电磁时间常数：Tl=0.001s
电机时间常数：TM=0.003s
经传动机构变速后输出的拖动力为：F=0~16N；与其配套的驱动器为：
MSDA021A1A，控制电压：UDA=0~±10V。
若忽略电动机的空载转矩和系统摩擦，就可以认为驱动器和机械传动装置
均为纯比例环节，并假设这两个环节的增益分别为 Kd 和 Km。
Kv
sT
m
1
2
sTT
lm
)(
sG
K
s
d
KKK
mv
16
F
max
10
U
max
K
s
6.1
即 D3(s)=1.6
电动机驱动器部分问题解决！
3.双闭环 PID 控制器设计
剩下的问题就是如何确定控制器
DSD
1
)(
1
'
和
（一）内环控制器的设计
)(
SDSD
)(
2
'
2
的结构和参数。
其中，Ks=1.6 为伺服电动机与减速机构的等效模型
4
自动控制原理课程设计
1.控制器的选择
内环系统未校正时的传递函数为
( )
s
( )
F s
6.4
2
12
s
对于内环反馈控制器 D2(s)可有 PD，PI，PID 三种可能的结构形式，怎么选
取呢？这里，不妨采用绘制各种控制器结构下“系统根轨迹”的办法加以分析比
较，从之选出一种比较适合的控制器结构。
各种控制器的开环传函的传递函数分别为：
6.4
2
s
6.4
P
:
PD
:
6.4
PI
:
PID
:
pK
12
6.4
K s
D
2
12
s
6.4
K s
p
2
12)
(
s s
2
6.4
K s
p
(
s s
K
p
K
I
6.4
2
6.4
K
I
K s
p
12)
在 MATLAB 下输入以下程序用“凑试”的方法画根轨迹图：
num=[分子];
den=[分母];
xlabel('Real Axis');
ylabel('Imag Axis');
axis([横、纵坐标范围]);
title('Root Locus');
grid;
rlocus(num,den)
下图为各种控制器下的系统根轨迹。
（a） PD
（b） PD
5
自动控制原理课程设计
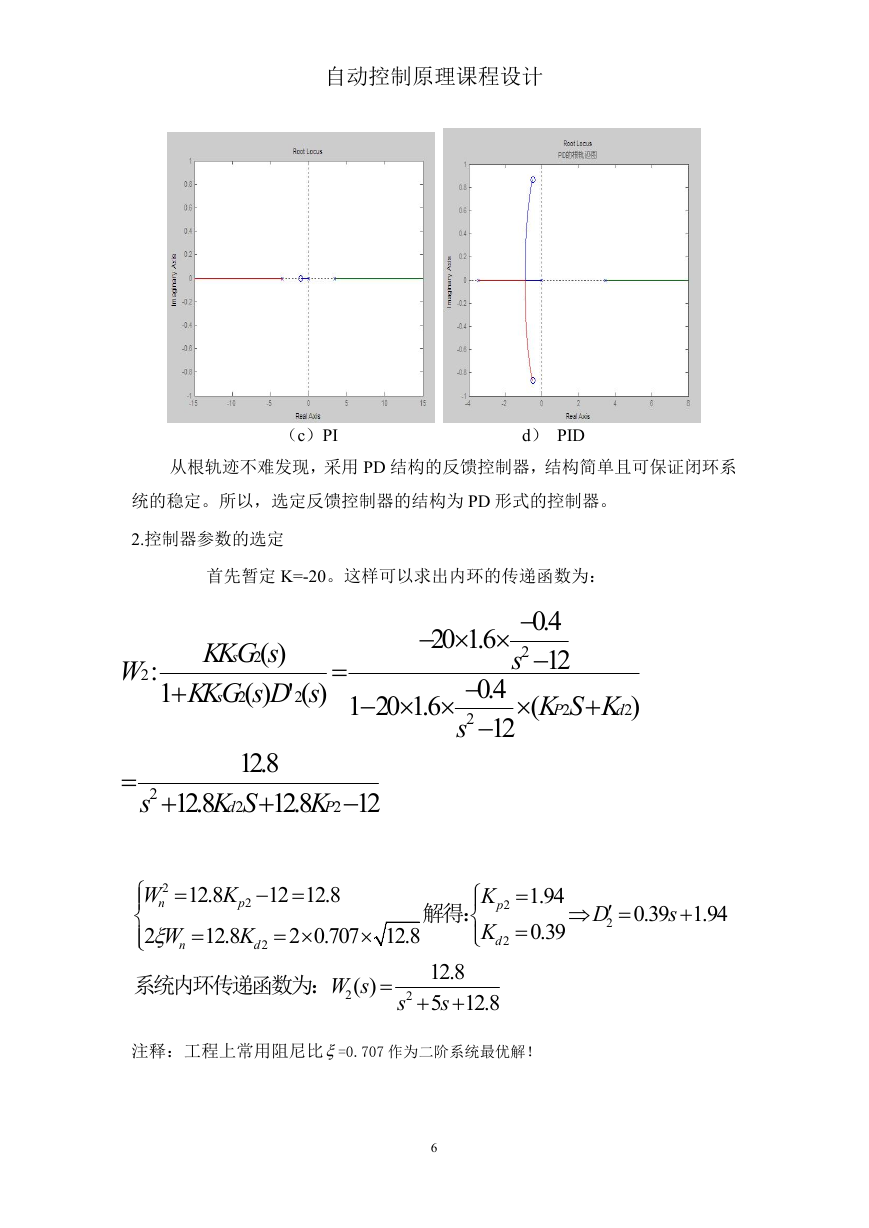
（c）PI
d） PID
从根轨迹不难发现，采用 PD 结构的反馈控制器，结构简单且可保证闭环系
统的稳定。所以，选定反馈控制器的结构为 PD 形式的控制器。
2.控制器参数的选定
首先暂定 K=-20。这样可以求出内环的传递函数为：
0.4
2
12
s
(
K S K
2
P
d
)
2
20 1.6
0.4
2
12
s
s
2
( )
KKG s
2
( ) ' ( ) 1 20 1.6
KKG s D s
2
s
12.8
12.8
K S
K
2
2
d
P
12
W
2
:
1
2
s
12.8
2
W
n
2
W
n
12.8
K
2
p
12.8
K
d
12 12.8
2 0.707
2
12.8
K
解得：
K
d
p
2
2
1.94
0.39
D
2
0.39
s
1.94
系统内环传递函数为：
( )
W s
2
12.8
5
s
12.8
2
s
注释：工程上常用阻尼比=0.707 作为二阶系统最优解！
6
自动控制原理课程设计
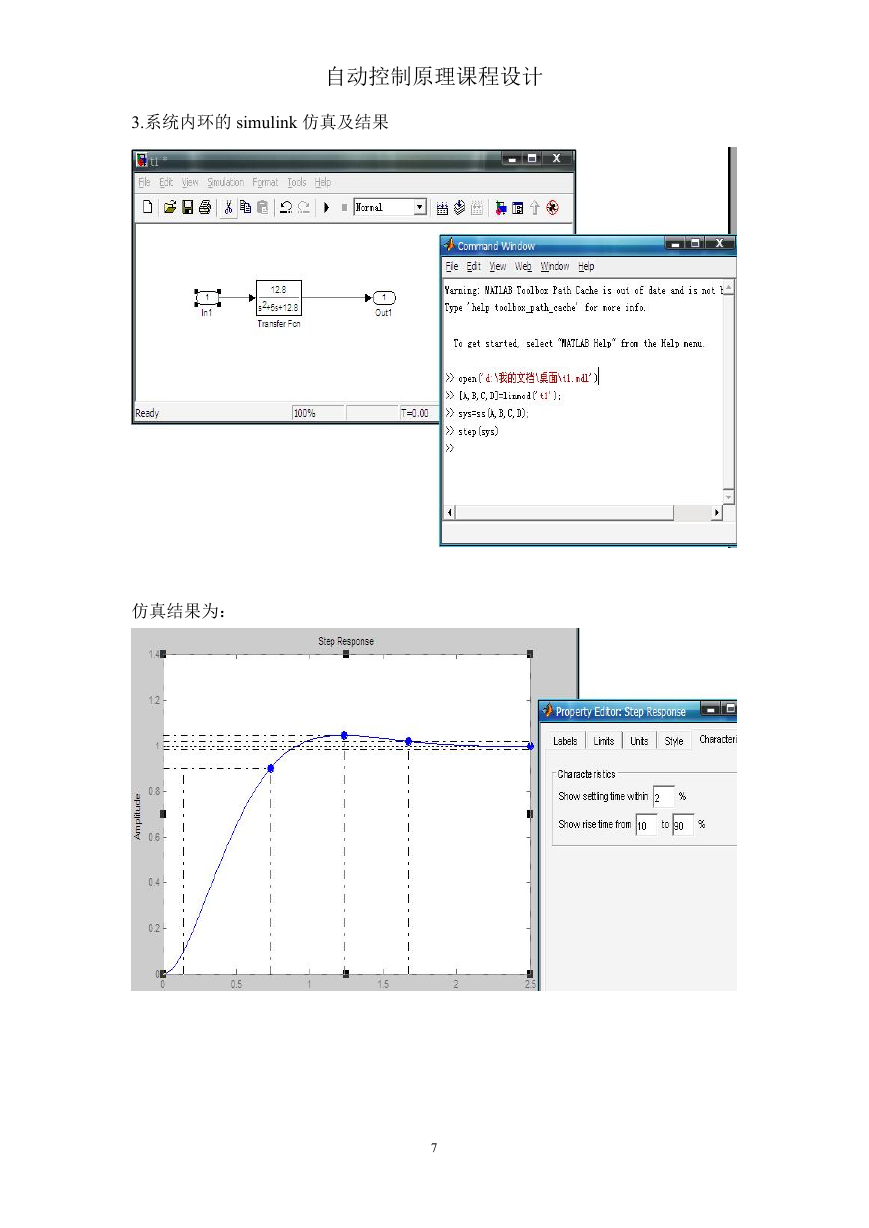
3.系统内环的 simulink 仿真及结果
仿真结果为：
7
自动控制原理课程设计
（二） 外环控制器的设计
( )
W s G s
( )
2
1
2
s
12.8
5
s
12.8
2
1.1
s
s
2
2
10 12.8( 1.1
s
5
s
2
(
s s
2
10)
12.8)
可见，系统开环传递函数可视为一个高阶（4 阶）且带有不稳定零点的“非
最小相位系统”，为了便于设计，需要首先对系统进行一些简化处理（否则，不
便利用经典控制理论与方法对它进行设计）。
１.系统外环模型的降阶
（1）对内环等效闭环传递函数的近似处理
( )
W s
2
12.8
5
s
2
s
12.8
...........(1)
将高次项 2s 忽略，有
( )
W s
2
12.8
s
12.8
5
1
0.39
s
1
..........(2)
近似条件可由频率特性导出，即
(
W j
)
2
(
2
)
j
12.8
5(
j
) 12.8
12.8
12.8
2
5
j
由（2）得： 2
(
W j
)
12.8
j
12.8
5
2
c
12.8
10
即：
c
1.13
（2）对象模型 G1(s)的近似处理
( )
G s
1
10
2
2
1.1
s
s
.........(3)
( )
G s
1
10
2
s
.........(4)
由（3）得：
(
G j
1
)
1.1(
2
2
)
j
j
10
2
10 1.1
2
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
