SAGE Algorithm for Channel Estimation and Data Detection with Tracking the Channel Variation in MIMO System Takao Someya Tomoaki Ohtsuki † †† † †† Graduate School of Science and Technology, Tokyo University of Science Dept. of Electrical Engineering, Tokyo University of Science E-mail:† j7304638@ed.noda.tus.ac.jp ††ohtsuki@ee.noda.tus.ac.jp 2641 Yamazaki, Noda, Chiba 278-8510 Japan Abstract— In recent years, Multiple-Input Multiple-Output (MIMO) systems with some transmit and receive antennas have attracted much attention in radio environments. In MIMO systems, the channel estimation is important to distinguish transmit signals from multiple transmit antennas. The Space- Alternating Generalized Expectation-maximization (SAGE) al- gorithm is known to be good for the channel estimation and the data detection. However, the SAGE algorithm has not been applied to MIMO systems. In this paper, we propose a SAGE algorithm for the channel estimation and data detection in MIMO systems. In addition, we propose a simplified SAGE algorithm for the channel estimation and the data detection with tracking the channel variation in MIMO systems. In the simplified SAGE algorithm, we divide a transmit frame into some subblocks and apply the SAGE algorithm to each subblock, and we use the channel estimates in the previous subblock as the initial channel estimates in the current subblock. According to the division of the transmit frame, the computational complexity is decreased. In addition, the simplified SAGE algorithm can track the channel variation by using the channel estimates transferred between the subblocks. I. INTRODUCTION The Expectation-Maximization (EM) algorithm [1] In recent years, Multiple-Input Multiple-Output (MIMO) systems with some transmit and receive antennas have at- tracted much attention as a promising technique for achiev- ing high bit-rate and high capacity transmission in radio environments. However, when the channel state information (CSI) is not perfect, MIMO systems are severely limited by signal interference from other transmit antennas. Therefore, in MIMO systems, to detect the transmitted signal from each transmit antenna, an accurate CSI is needed at the receiver. is known to be good for the channel estimation and the data detection in Orthogonal Frequency-Division Multiplexing (OFDM) systems [2] and Space-Time Block coded (STBC) MIMO systems [3]. The EM algorithm is an iterative method to approximate the maximum likelihood (ML) estimation when a direct computation is computationally limited. The EM algorithm makes use of the log-likelihood function in a two-step iterative procedure. At the first step of the EM algorithm, referred to as the Expectation-step (E-step), the expectation of the log-likelihood function is calculated. In the second step referred to as the Maximization-step (M- step) the parameters are updated by maximizing the function derived from the E-step. However, the EM algorithm updates all the parameters for the channel estimation and the data detection simultaneously, which results in a disadvantage of slow convergence. In addition, the EM algorithm can not track the channel variation well. The Space-Alternating Generalized Expectation-maximization (SAGE) algorithm [4] has been proposed for accelerating the convergence of the Input DEMUX 1 2 N Channel 1 2 M Output MUX Transmitter Receiver Fig. 1. A Multiple-Input Multiple-Output (MIMO) system with N transmit antennas and M receive antennas EM algorithm. The SAGE algorithm updates the parameters sequentially by alternating between the subset of parame- ters. The SAGE algorithm was applied to Direct-Sequence Code-Division Multiple-Access (DS-CDMA) systems [5] and Space-Time Coding (STC) systems [6]. However, the SAGE algorithm has not been applied to MIMO systems. In this paper, we propose a SAGE algorithm for the channel estimation and the data detection in MIMO systems. In addition, we propose a simplified SAGE algorithm for the channel estimation and the data detection with tracking the channel variation in MIMO systems. In the simplified SAGE algorithm, we divide a transmitted frame into some subblocks and apply the SAGE algorithm to each subblock, and we use the channel estimates in the previous subblock as the initial channel estimates in the current subblock. According to the division of the transmitted frame, the computational complex- ity is decreased. In addition, the simplified SAGE algorithm can track the channel variation by using the channel estimates transferred between the subblocks. We show that the proposed SAGE algorithm can achieve the better bit error rate (BER) than the ML detection with training symbols. We also show that the proposed simplified SAGE algorithm can achieve the better BER with less computational complexity than the proposed SAGE algorithm. In particular, we show that the proposed simplified SAGE algorithm improves BER more significantly with less computational complexity in the fast fading environments than in the slow fading environments. II. SYSTEM MODEL n,··· , X L We consider the MIMO system with N transmit antennas and M receive antennas shown in Fig. 1. One transmitted n ]T (n = 1,··· , N) frame of L symbols Xn = [X 1 is transmitted from the n-th transmit antenna. X L n is the transmitted symbol from the n-th transmit antenna at the L- th symbol. The notation [·]T denotes the transpose operation. A training sequence of p symbols is inserted in the head of each transmitted frame. The training sequence is orthogonal between each transmit antenna. At the the k-th symbol, IEEE Communications Society Globecom 2004 3651 0-7803-8794-5/04/$20.00 © 2004 IEEE 

N Y k m = H k n,mX k n + W k m, k = 1,··· , L (1) n=1 where H k n,m is the channel frequency response at the k- th symbol, corresponding to the channel between the n- th transmit antenna and the m-th receive antenna. W k m is an additive white Gaussian noise (AWGN) with zero-mean and variance σ2 at the k-th symbol on the m-th receive antenna. We denote the received signal vector by Ym = [Y 1 m]T , then eq. (1) can be expressed as m,··· , Y L m, Y 2 Ym = XHm + Wm (2) where X = [diag(X1)··· diag(XN )] is an L×N L transmit- ted matrix, Hm = [H1,m ··· HN,m]T is an N L × 1 channel n,m]T is an L × 1 channel vector, Hn,m = [H 1 m]T is an L × 1 AWGN vector, and Wm = [W 1 vector. The notation diag(·) denotes the diagonal matrix. n,m,··· , H L m,··· , W L III. EM ALGORITHM AND SAGE ALGORITHM A. EM Algorithm [1][2] Let a ∈ A be a set of the parameters to be estimated from some observed data y ∈ Y with conditional probability density p(y|a). It is difficult to derive the ML estimates of a from p(y|a) when a direct computation is computationally limited. In such a situation, the EM algorithm provides an iterative scheme to approach the ML estimate of a. The derivation of the algorithm relies on a complete unobservable data z ∈ Z, and if the complete data z can be observed, the ML estimates of a are easily obtained. The data z is such that the observed data y could be obtained through a many-to-one mapping z → y(z). The observed data y is referred to as the incomplete data within the EM scheme. The EM algorithm makes use of the log-likelihood function for the complete data in a two-step iterative procedure. At the i-th iteration, the first step of the EM algorithm, referred to as the Expectation-step (E-step), can be expressed as Q(a|a[i]) E{Λ(z|a)|y, a[i]} (5) (6) We explain the SAGE algorithm proposed by Fessler et al. [4]. In the SAGE algorithm only a subset aS of the parameter vector a indexed by S = S[i] is updated without updating all the parameters at one iteration. The other subset aS of a is kept. In consequence, the SAGE algorithm converges much faster than the EM algorithm. At the i-th iteration, the E-step can be expressed as Q(aS|a[i]) E{Λ(z|aS, a[i] S )|y, a[i]}. In the M-step, only bS is updated as follows QS(aS|a[i]) a[i+1] S = arg max aS a[i+1] S = a[i] S . Provided that z is a complete data for each selected subset aS under the assumption that the parameters in the subset aS are known, the SAGE algorithm exhibits the monotonicity property. IV. PROPOSED CHANNEL ESTIMATION AND DATA DETECTION A. Initial Estimation with Training Symbols We apply the minimum mean square error (MMSE) esti- mation to the initial channel estimation. Since the channel vector Hm and AWGN Wm are uncorrelated, the channel vector ˜Htr m derived from the training symbol block Xtr is given by [7] m = Rtr −1 Ytr hh(Xtr)H + σ2Ip hh(Xtr)H XtrRtr m (7) ˜Htr to be known at where Rtr hh is the covariance matrix of the channel in the training symbols, and we assume it the receiver. Ip denotes the p×p identity matrix, and (·)H denotes the Hermitian matrix. m derived from eq. (7) m] = [ ¯H1,m, ¯H2,m,··· , ¯HN,m] over p training symbols (E[ ˜Htr ). According to the ML detection, the initial estimate of the 1 ,··· , ˆX k transmitted frame ˆX k = [ ˆX k N ] derived from the averaged channel estimate E[ ˜Htr m] is given by We average the channel estimate ˜Htr Y k m − N n=1 M m=1 2 X ∗ ¯Hn,m , k = p + 1,··· , L ˜H k n,m, n = 1,··· , N. (8) where a[i] is the estimate of the parameter vector at the i-th iteration. Λ(·) denotes the log-likelihood function. In the second step referred to as a Maximization-step (M- step) the estimate of the parameter vector is updated according to ˆX k = arg min ¯Hn,m = 1 p X p k=0 a[i+1] = arg max a Q(a|a[i]). (3) (4) received signal at the m-th receive antenna is expressed as B. SAGE Algorithm [4] Note that since the complete data z is actually unavailable, the algorithm maximizes the conditional expectation Λ(z|a) instead, given the incomplete data y and the most recent estimate of the parameter vector a to be estimated. If a[i] is the estimate of the parameter vector generated by the EM algorithm starting from an initial value a[0], then Λ(y|a[i]) is non-decreasing (monotonicity property). The performance of the EM algorithm to find a global maximum depends on the initial value a[0]. The convergence rate of the EM algorithm is related to the fraction of a missing information. We apply the symbol sequence derived from eq. (8) to the initial estimate (X[0]) of the symbol sequence of the SAGE algorithm that is explained in the next subsection IV. B. B. Channel Estimation and Data Detection with SAGE Algo- rithm In this subsection, since the estimate function of each receive antenna is equivalent, the receive antenna index m is omitted. According to the section III, the parameter vector a to be estimated is the transmitted symbol matrix X, and the incomplete data y is the received signal vector Y. We select IEEE Communications Society Globecom 2004 3652 0-7803-8794-5/04/$20.00 © 2004 IEEE 

the set {Y, H} of the received signal vector Y and the channel vector H to the complete data z (z = {Y, H} ). The log-likelihood function of the complete data z is expressed as [5] Λ(z|b) = Λ(Y, H|X) = Λ(Y|H, X) + Λ(H|X) (9) where the second term Λ(H|X) of eq. (9) is independent of X and can be thus discarded. According to the Gaussian distribution, the first term Λ(Y|H, X) of eq. (9) becomes [8] L Λ(Y|H, X) =   L   Λ(Y k|H, X)    − 1 Y k− N 2 H k k=1 = log nX k n exp 1√ 2πσ2 k=1 2σ2 n=1 (10) where we omit the terms of constant. This conditional log- likelihood function Λ(Y k|H, X) is rewritten as ∗ N ∗ Λ(Y k|X, H) = Y k ∗ N N − N nX k n nX k n H k H k H k H k Y k n=1 n=1 + nX k n nX k n (11) n=1 n=1 where (·)∗ denotes the complex conjugate. Here, we select a subset aS of a in the SAGE algorithm to the transmitted frame Xn from the n-th transmit antenna (aS = Xn). Neglecting the terms independent of Xn, at the i-th iteration, the E-step of eq. (5) becomes Q(Xn|X[i] L L Y, X[i] Λ(Y k|Xn, Xn [i], H) = E k=1 ) Y k ∗ n X k n) ( ˆH k[i] + (Y k ∗ ˆH k[i] ) n X k n = k=1 − ( ˆH k[i] n X k n) ˆH k[i] j X k j [i] ∗ N N j=1 j=n − ˆH k[i] n X k n ( ˆH k[i] j X k j [i] ∗ − ˆH k[i] ) n X k n( ˆH k[i] ∗ n X k n) j=1 j=n ˆH[i] = E{H|Y, X[i]} (12) where Xn = aS is the transmitted symbol vector by can- celing the components of Xn in X, and the superscript [i] denotes the number of iterations. At the i-th iteration, only the symbol of the n-th (n = (i mod N)+1) transmit antenna is updated, and the other symbols are not updated. Therefore, as the iteration index i increases, the transmit antenna index n of updating the transmitted symbol also increases. At the (N + 1)-th iteration, the first updated symbol is updated again. According to the MMSE estimation, the conditional distribution of H given Y and X[i] is derived as E{H|Y, X[i]} = Rhh −1 X[i]Rhh + σ2IN H H X[i] X[i] Y (13) where Rhh is the covariance matrix of the channel vector H that is assumed to be known at the receiver. We differentiate n)∗ the function in eq. (12) with respect to (X k  ∇(X k n)∗{Q(Xn|X[i])} = L ( ˆH k[i] ∗Y k − ( ˆH k[i] n ) ∗ N j X k j ˆH k[i] n ) [2][7] as follows   . [i] − | ˆH k[i] n |2X k n k=1 j=1 j=n (14) The function in eq. (12) is maximized by setting the gradient ∇(X k n)∗{Q(Xn|X[i])} to zero. Therefore, at the (i + 1)-th iteration, the estimate of the transmitted symbol X k is  n given by  .  ( ˆH k[i] ∗Y k − ( ˆH k[i] n ) ∗ N [i+1] = j X k j ˆH k[i] n ) X k n [i+1] [i] 1 ˆH k[i] n 2 j=1 j=n (15) M The transmitted symbols are estimated in each receive an- tenna. In the next subsection IV. C, we explain a combining method of the transmitted symbols to be estimated in each receive antenna in our proposed algorithm. C. Maximum Ratio Combining (MRC) Maximum ratio combining (MRC) weights each transmit- ted symbol estimate with its channel estimate as follows X k n [i+1] = F | ˆH k[i] n |2X k n,m [i+1] , k = 1,··· , L m=1 (16) where F{·} denotes the hard decision. The MRC is used with each iteration. The transmitted symbol estimate calculated by MRC is used at the next iteration in each receive antenna. V. TRACKING THE CHANNEL WITH LOW COMPLEXITY The computation of eq. (13) requires the inverse matrix of a transmitted frame with a length of L, where the order of its computational complexity is O(L3). Additionally, applying the SAGE algorithm to the whole transmitted frame can not track channel variation well, because the accuracy of the initial data detection in a frame end is degraded. Therefore, we divide a transmitted frame into Subblocks (SBs) of every l symbols, Xn = {Xn[1],··· , Xn[B],··· , Xn[L/l]} and apply the SAGE algorithm to each SB. Here, B denotes the SB index. To track the channel variation, we use the channel estimate of the last l-th symbol in the previous SB as the initial channel estimate in the current SB. By division of the transmitted frame, the computation of eq. (13) is reduced. The order of its computational complexity of a transmitted frame l × l3) = O(Ll2). In addition, by using the becomes O( L channel estimate in the previous SB as the initial estimate in the current SB, the proposed algorithm can track the channel variation. According to the ML detection, the initial estimates of in the current SB, X k[0][B] = the transmitted symbol IEEE Communications Society Globecom 2004 3653 0-7803-8794-5/04/$20.00 © 2004 IEEE 

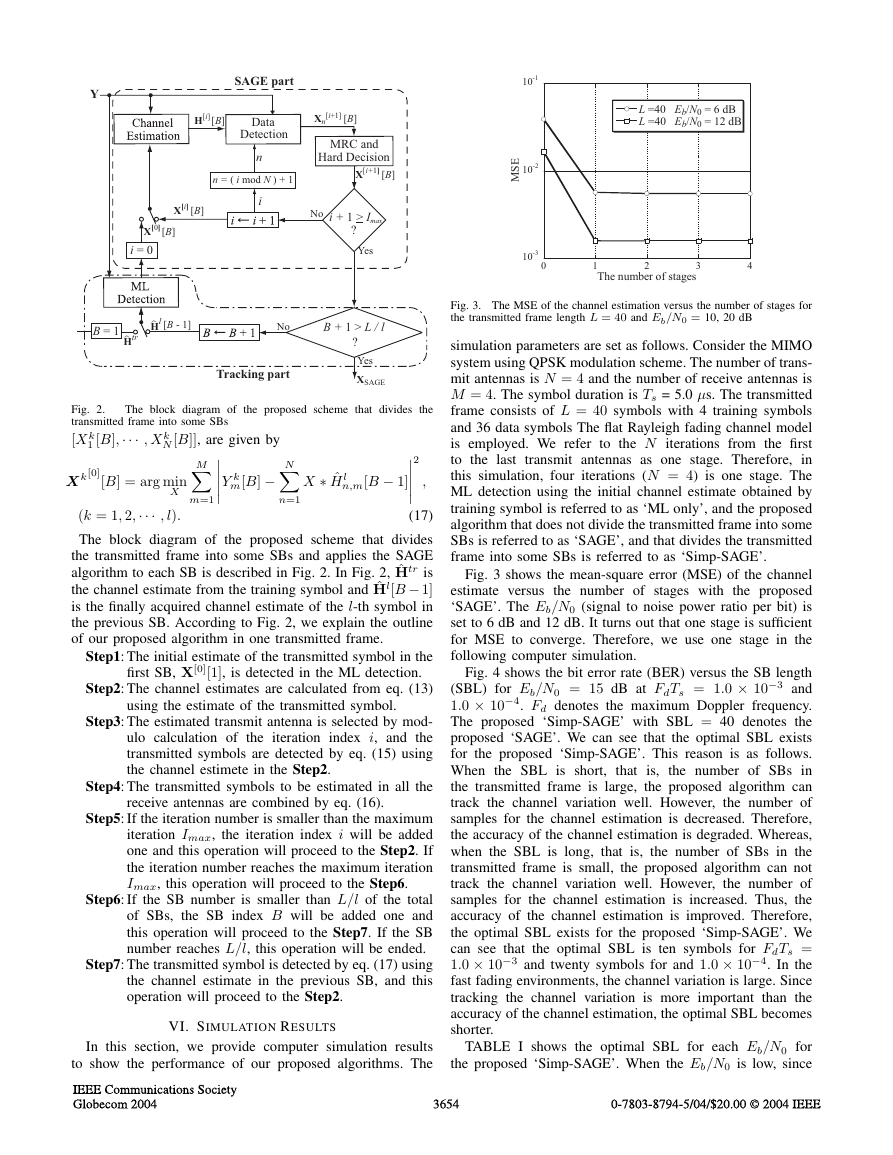
Y SAGE part H[i] [B] Data Detection n n = ( i mod N ) + 1 Xn [i+1] [B] MRC and Hard Decision X[i+1] [B] X[i] [B] i X[0] [B] i = 0 No i + 1 > Imax ? Yes l [B - 1] H B = 1 tr H No B + 1 > L / l Tracking part ? Yes XSAGE The block diagram of the proposed scheme that divides the Fig. 2. transmitted frame into some SBs [X k 1 [B],··· , X k N [B]], are given by M Y k m[B] − N 2 X ∗ ˆH l n,m[B − 1] , X n=1 m=1 X k[0][B] = arg min (k = 1, 2,··· , l). (17) The block diagram of the proposed scheme that divides the transmitted frame into some SBs and applies the SAGE algorithm to each SB is described in Fig. 2. In Fig. 2, ˆHtr is the channel estimate from the training symbol and ˆHl[B − 1] is the finally acquired channel estimate of the l-th symbol in the previous SB. According to Fig. 2, we explain the outline of our proposed algorithm in one transmitted frame. Step1: The initial estimate of the transmitted symbol in the first SB, X[0][1], is detected in the ML detection. Step2: The channel estimates are calculated from eq. (13) using the estimate of the transmitted symbol. Step3: The estimated transmit antenna is selected by mod- ulo calculation of the iteration index i, and the transmitted symbols are detected by eq. (15) using the channel estimete in the Step2. Step4: The transmitted symbols to be estimated in all the receive antennas are combined by eq. (16). Step5: If the iteration number is smaller than the maximum iteration Imax, the iteration index i will be added one and this operation will proceed to the Step2. If the iteration number reaches the maximum iteration Imax, this operation will proceed to the Step6. Step6: If the SB number is smaller than L/l of the total of SBs, the SB index B will be added one and this operation will proceed to the Step7. If the SB number reaches L/l, this operation will be ended. Step7: The transmitted symbol is detected by eq. (17) using the channel estimate in the previous SB, and this operation will proceed to the Step2. VI. SIMULATION RESULTS In this section, we provide computer simulation results to show the performance of our proposed algorithms. The 10-1 E S M 10-2 10-3 0 L =40 Eb/N L =40 Eb/N 0 = 6 dB 0 = 12 dB 3 1 The number of stages 2 4 Fig. 3. The MSE of the channel estimation versus the number of stages for the transmitted frame length L = 40 and Eb/N0 = 10, 20 dB simulation parameters are set as follows. Consider the MIMO system using QPSK modulation scheme. The number of trans- mit antennas is N = 4 and the number of receive antennas is M = 4. The symbol duration is Ts = 5.0 µs. The transmitted frame consists of L = 40 symbols with 4 training symbols and 36 data symbols The flat Rayleigh fading channel model is employed. We refer to the N iterations from the first to the last in this simulation, four iterations (N = 4) is one stage. The ML detection using the initial channel estimate obtained by training symbol is referred to as ‘ML only’, and the proposed algorithm that does not divide the transmitted frame into some SBs is referred to as ‘SAGE’, and that divides the transmitted frame into some SBs is referred to as ‘Simp-SAGE’. transmit antennas as one stage. 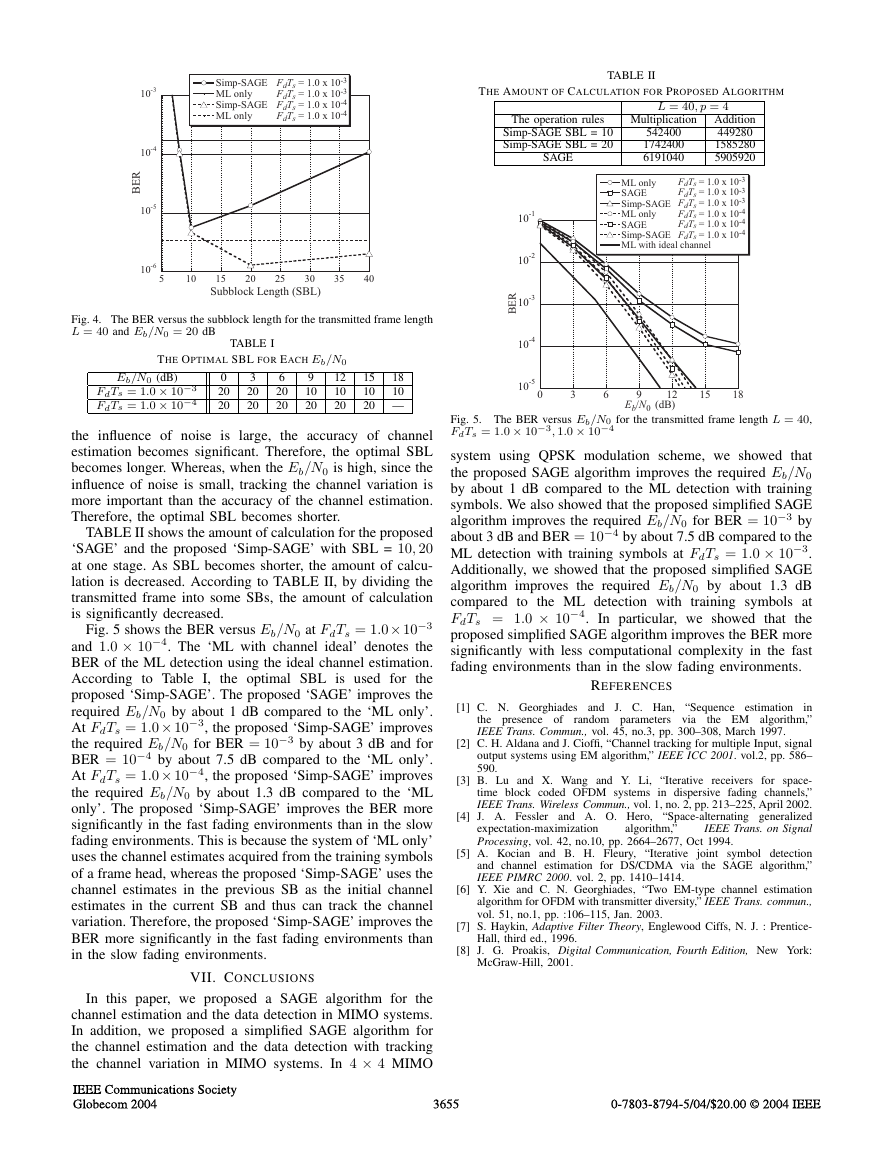Therefore, that Fig. 3 shows the mean-square error (MSE) of the channel estimate versus the number of stages with the proposed ‘SAGE’. The Eb/N0 (signal to noise power ratio per bit) is set to 6 dB and 12 dB. It turns out that one stage is sufficient for MSE to converge. Therefore, we use one stage in the following computer simulation. Fig. 4 shows the bit error rate (BER) versus the SB length (SBL) for Eb/N0 = 15 dB at FdTs = 1.0 × 10−3 and 1.0 × 10−4. Fd denotes the maximum Doppler frequency. The proposed ‘Simp-SAGE’ with SBL = 40 denotes the proposed ‘SAGE’. We can see that the optimal SBL exists for the proposed ‘Simp-SAGE’. This reason is as follows. When the SBL is short, the number of SBs in the transmitted frame is large, the proposed algorithm can track the channel variation well. However, the number of samples for the channel estimation is decreased. Therefore, the accuracy of the channel estimation is degraded. Whereas, when the SBL is long, that is, the number of SBs in the transmitted frame is small, the proposed algorithm can not track the channel variation well. However, the number of samples for the channel estimation is increased. Thus, the accuracy of the channel estimation is improved. Therefore, the optimal SBL exists for the proposed ‘Simp-SAGE’. We can see that the optimal SBL is ten symbols for FdTs = 1.0 × 10−3 and twenty symbols for and 1.0 × 10−4. In the fast fading environments, the channel variation is large. Since tracking the channel variation is more important than the accuracy of the channel estimation, the optimal SBL becomes shorter. is, TABLE I shows the optimal SBL for each Eb/N0 for the proposed ‘Simp-SAGE’. When the Eb/N0 is low, since IEEE Communications Society Globecom 2004 3654 0-7803-8794-5/04/$20.00 © 2004 IEEE 

10-3 10-4 R E B 10-5 10-6 Simp-SAGE ML only Simp-SAGE ML only FdTs = 1.0 x 10-3 FdTs = 1.0 x 10-3 FdTs = 1.0 x 10-4 FdTs = 1.0 x 10-4 5 10 15 20 25 30 35 40 Subblock Length (SBL) Fig. 4. The BER versus the subblock length for the transmitted frame length L = 40 and Eb/N0 = 20 dB TABLE I Eb/N0 (dB) FdTs = 1.0 × 10−3 FdTs = 1.0 × 10−4 THE OPTIMAL SBL FOR EACH Eb/N0 12 10 20 0 20 20 3 20 20 6 20 20 9 10 20 18 15 10 10 20 — the influence of noise is large, the accuracy of channel estimation becomes significant. Therefore, the optimal SBL becomes longer. Whereas, when the Eb/N0 is high, since the influence of noise is small, tracking the channel variation is more important than the accuracy of the channel estimation. Therefore, the optimal SBL becomes shorter. TABLE II shows the amount of calculation for the proposed ‘SAGE’ and the proposed ‘Simp-SAGE’ with SBL = 10, 20 at one stage. As SBL becomes shorter, the amount of calcu- lation is decreased. According to TABLE II, by dividing the transmitted frame into some SBs, the amount of calculation is significantly decreased. Fig. 5 shows the BER versus Eb/N0 at FdTs = 1.0×10−3 and 1.0 × 10−4. The ‘ML with channel ideal’ denotes the BER of the ML detection using the ideal channel estimation. According to Table I, the optimal SBL is used for the proposed ‘Simp-SAGE’. The proposed ‘SAGE’ improves the required Eb/N0 by about 1 dB compared to the ‘ML only’. At FdTs = 1.0× 10−3, the proposed ‘Simp-SAGE’ improves the required Eb/N0 for BER = 10−3 by about 3 dB and for BER = 10−4 by about 7.5 dB compared to the ‘ML only’. At FdTs = 1.0× 10−4, the proposed ‘Simp-SAGE’ improves the required Eb/N0 by about 1.3 dB compared to the ‘ML only’. The proposed ‘Simp-SAGE’ improves the BER more significantly in the fast fading environments than in the slow fading environments. This is because the system of ‘ML only’ uses the channel estimates acquired from the training symbols of a frame head, whereas the proposed ‘Simp-SAGE’ uses the channel estimates in the previous SB as the initial channel estimates in the current SB and thus can track the channel variation. Therefore, the proposed ‘Simp-SAGE’ improves the BER more significantly in the fast fading environments than in the slow fading environments. THE AMOUNT OF CALCULATION FOR PROPOSED ALGORITHM TABLE II L = 40, p = 4 Multiplication 542400 1742400 6191040 Addition 449280 1585280 5905920 ML only SAGE Simp-SAGE ML only SAGE Simp-SAGE ML with ideal channel FdTs = 1.0 x 10-3 FdTs = 1.0 x 10-3 FdTs = 1.0 x 10-3 FdTs = 1.0 x 10-4 FdTs = 1.0 x 10-4 FdTs = 1.0 x 10-4 The operation rules Simp-SAGE SBL = 10 Simp-SAGE SBL = 20 SAGE 10-1 10-2 10-3 R E B 10-4 10-5 0 3 6 9 Eb/N 12 0 (dB) 15 18 Fig. 5. The BER versus Eb/N0 for the transmitted frame length L = 40, FdTs = 1.0 × 10−3, 1.0 × 10−4 system using QPSK modulation scheme, we showed that the proposed SAGE algorithm improves the required Eb/N0 by about 1 dB compared to the ML detection with training symbols. We also showed that the proposed simplified SAGE algorithm improves the required Eb/N0 for BER = 10−3 by about 3 dB and BER = 10−4 by about 7.5 dB compared to the ML detection with training symbols at FdTs = 1.0 × 10−3. Additionally, we showed that the proposed simplified SAGE algorithm improves the required Eb/N0 by about 1.3 dB compared to the ML detection with training symbols at FdTs = 1.0 × 10−4. In particular, we showed that the proposed simplified SAGE algorithm improves the BER more significantly with less computational complexity in the fast fading environments than in the slow fading environments. REFERENCES [1] C. N. Georghiades and J. C. Han, “Sequence estimation in the EM algorithm,” the presence of IEEE Trans. Commun., vol. 45, no.3, pp. 300–308, March 1997. random parameters via [2] C. H. Aldana and J. Cioffi, “Channel tracking for multiple Input, signal output systems using EM algorithm,” IEEE ICC 2001. vol.2, pp. 586– 590. [3] B. Lu and X. Wang and Y. Li, “Iterative receivers for space- time block coded OFDM systems in dispersive fading channels,” IEEE Trans. Wireless Commun., vol. 1, no. 2, pp. 213–225, April 2002. [4] J. A. Fessler and A. O. Hero, “Space-alternating generalized IEEE Trans. on Signal expectation-maximization Processing, vol. 42, no.10, pp. 2664–2677, Oct 1994. algorithm,” [5] A. Kocian and B. H. Fleury, “Iterative joint symbol detection and channel estimation for DS/CDMA via the SAGE algorithm,” IEEE PIMRC 2000. vol. 2, pp. 1410–1414. [6] Y. Xie and C. N. Georghiades, “Two EM-type channel estimation algorithm for OFDM with transmitter diversity,” IEEE Trans. commun., vol. 51, no.1, pp. :106–115, Jan. 2003. [7] S. Haykin, Adaptive Filter Theory, Englewood Ciffs, N. J. : Prentice- [8] J. G. Proakis, Digital Communication, Fourth Edition, New York: Hall, third ed., 1996. McGraw-Hill, 2001. VII. CONCLUSIONS In this paper, we proposed a SAGE algorithm for the channel estimation and the data detection in MIMO systems. In addition, we proposed a simplified SAGE algorithm for the channel estimation and the data detection with tracking the channel variation in MIMO systems. In 4 × 4 MIMO IEEE Communications Society Globecom 2004 3655 0-7803-8794-5/04/$20.00 © 2004 IEEE