模糊聚类分析法在经济区域划分中的应用.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.38M 资料格式：pdf 举报版权申诉

weixin_38744962-12135647-4744302543017274820.pdf-第1页.png

第1页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第2页.png

第2页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第3页.png

第3页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第4页.png

第4页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第5页.png

第5页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第6页.png

第6页 / 共7页

weixin_38744962-12135647-4744302543017274820.pdf-第7页.png

第7页 / 共7页

1. 引言

2. 模糊聚类分析方法

2.1相关定义与定理

2.2编网法

3. 模糊聚类分析法经济区域划分中的应用

3.1 符号说明

3.2影响我国经济发展的主要因素

3.3 经济区域划分

3.3.1建立模糊集合

3.3.2利用贴近度建立模糊相似矩阵

3.3.3分类结果

3.3.4分类结果评价

4. 结语

模糊聚类分析法在经济区域划分中的应用徐鹏1，杨甲2，蔡成标1 http://www.paper.edu.cn 1 西南交通大学牵引动力国家重点实验室，四川成都 (610031) 2 同济大学交通运输工程学院，上海 (201804） E-mail: gslzxupeng@163.com 摘要：本文针对经济区域划分问题，利用 Matlab 软件绘制出经济指标所占 GDP 权重的分布图，得出影响经济发展的主要因素。同时采用模糊数学原理利用贴近度建立模糊相似矩阵，由编网法聚类得到经济区域划分的结果。关键词：模糊聚类分析；经济区域划分；模糊数学；编网法中图分类号：F224.7 1. 引言 “十一五”期间我国区域经济发展仍面临区域发展不平衡这一核心问题。目前东中西部人均差距不断扩大；外贸和利用外资不平衡，东部地区处于绝对优势地位；市场经济体制发展和产业结构调整不均衡，东部地区逐渐与国际接轨的同时，中西部地区却在所有制结构和产业结构上的调整缓慢。缓慢的经济发展和区域经济发展不平衡等因素严重制约了我国的经济建设，因而必须坚持从实际出发，深入分析各个地区经济发展的历史过程与现状，贯彻因时、因地制宜的原则，对处于不同发展阶段的地区经济采取不同的管理策略和方法。正确把握我国经济发展规律，找准经济发展的薄弱环节和经济发展的不平衡区域，宏观上给予倾斜性政策调控促使我国经济快速发展。为了对我国各经济区域经济发展水平有较清晰、较具体的认识，本文根据某年我国 30 个省市自治区（重庆除外）经济发展情况的八项指标的统计数据（来源于中国统计年鉴）采用模糊聚类分析方法按各省市自治区经济发展济发展指标对我国的经济区域进行聚类分析。 2. 模糊聚类分析方法聚类分析是指对事物按一定要求进行分类的数学方法。聚类分析是数理统计中研究“物以类聚”的一种多元分析方法，即用数学定量地确定样品的亲疏关系，从而客观地分型划类。由于事物本身在很多情况下都带有模糊性，因此把模糊数学的方法引入聚类分析，就能使分类更切合实际。模糊聚类分析应用广泛，如在气象预报、地质、环境、林业、农业科学、经济等多方面已取得可喜的成果。如：王立新和刘华民利用模糊聚类法对我国城市内河水质污染分类作出了研究[1]；田丽等利用模糊聚类法对水环境质量进行了评价[2]；王云峰和杨冬利用模糊聚类分析法对山东区域经济进行了分类与研究[3]。 2.1 相关定义与定理定义 1 设给定的论域U 上的一个模糊关系 = ( r )ij n n × 如果它满足： R （1）自反性 iir = 。 1 r r j i ( , = （2）对称性 ij R⊆ （3）传递性 R R 。 = r )ij n n ji = 1,2 n ) 。 ( R 则称在这个定义中直观地看，自反性是矩阵的对角线上的元素全是 1。对称性是 R 是一个模糊等价关系。 × 为对称矩 - 1 -

。而传递性却不易直接看出，需要计算 r ij r= ji 阵，即自身的合成，然后看其是否满足： R R R⊆ 。表 1 某年 30 个省市自治区（重庆）除外的经济发展指标 http://www.paper.edu.cn R R （并记作 2R ），它表示 R 和它省份 GDP 居民消固定资产职工平货物周转费水平投资均工资量居民消商品零费价格售价格指数指数工业总产值北京天津河北山西内蒙辽宁吉林黑龙江上海江苏浙江安徽福建江西山东河南湖北湖南广东广西海南四川贵州云南西藏陕西甘肃青海宁夏 1394.89 920.11 2849.52 1092.48 832.88 2793.37 1129.20 2014.53 2462.57 5155.25 3524.79 2003.58 2160.52 1205.11 5002.34 3002.74 2391.42 2195.70 5381.72 1606.15 364.17 3534.00 630.07 1206.68 55.98 1000.03 553.35 165.31 169.75 2505 2720 1258 1250 1387 2397 1872 2334 5343 1926 2249 1254 2320 1182 1527 1034 1527 1408 2699 1314 1814 1261 942 1261 1110 1208 1007 1445 1355 519.01 345.46 704.87 290.90 250.23 387.99 320.45 435.73 996.48 1434.95 1006.39 474.00 553.97 282.84 1229.55 670.35 571.68 422.61 1639.83 382.59 198.35 822.54 150.84 334.00 17.87 300.27 114.81 47.76 61.98 8144 6501 4839 4721 4134 4911 4430 4145 9279 5943 6619 4609 5857 4211 5154 4344 4685 4797 8250 5105 5340 4645 4475 5149 7382 4396 5493 5753 5079 373.9 342.8 2033.3 717.3 781.7 1371.1 497.4 824.8 207.4 1025.5 754.4 908.3 609.3 411.7 1196.6 1574.4 849.0 1011.8 656.5 556.0 232.1 902.3 301.1 310.4 4.2 500.9 507.0 61.6 121.8 新疆 1469 834.57 5348 定义 2 设给定的论域U 上的一个模糊关系 R 376.95 339.0 )ij n n × r= ( （1）自反性 iir = 。 1 - 2 - 117.3 115.2 115.2 116.9 117.5 116.1 115.2 116.1 118.7 115.8 116.6 114.8 115.2 116.9 117.6 116.5 120.0 119.0 114.0 118.4 113.5 118.5 121.4 121.3 117.3 119.0 119.8 118.0 117.1 119.7 112.6 110.6 115.8 115.6 116.8 114.0 114.2 114.3 113.0 114.3 113.5 112.7 114.4 115.9 114.2 114.9 116.6 115.5 111.6 116.4 111.3 117.0 117.2 118.1 114.9 117.0 116.5 116.3 115.3 116.7 843.43 582.51 1234.85 697.25 419.39 1840.55 762.47 1240.37 1642.95 2026.64 916.59 824.14 433.67 571.84 2207.69 1367.92 1220.72 843.83 1396.35 554.97 64.33 1431.81 324.72 716.65 5.57 600.98 468.79 105.80 114.40 428.76 如果它满足：

（2）对称性 r ij = r ji i ( , j = 1,2 n ) 。 = ( r )ij n n × 是一个模糊相似关系。 http://www.paper.edu.cn ), 对任意 [0,1] λ∈ ，记 R r ij ) λ λ= ( ，其中：则称 R ≥ < r λ ij r= ( ij λ λ R 定义 3 设给定模糊矩阵 r ij r ij 1 ⎧ = ⎨ 0 ⎩ 为 R R r ( )ij 的λ截矩阵。 λ λ= 则称 i A B A B A B 定义 4 记( , [ ) = 定理 1 若模糊关系矩阵 R )] 2 ，则 ( (1 和 B 称之为 A + − 是模糊等价关系，则对于任意 [0,1] λ∈ )A B , 的贴近度。，所截得λ截矩阵 Rλ 也是等价关系。根据这个定理可以知道，模糊等价关系 R 确定之后，对给定的 [0,1] λ∈ ，便可相应得到一普通等价关系 Rλ，这也就是说可以决定一个λ水平的分类。定理 2 若 0 λ λ≤ 2 ≤ 1 ≤ 1 该定理所述的性质是说明 2 则 Rλ 所分出的每一类必是 Rλ 的分法比 Rλ 的分法细。 1 2 Rλ 的某一类的子类。 1 2.2 编网法对于模糊聚类我们一般选取一种标定方法来构成模糊矩阵，往往只满足自反性和对称性，而不一定满足传递性，即这种模糊关系属于模糊相似关系。这就要求我们首先由模糊相似关系改造成模糊等价关系，然后再完成聚类分析。为此有不少人企图寻求直接由模糊相似矩阵直接进行聚类的方法，在 1979 年吴望名曾提出最大树的方法，在 1980 年赵汝怀又提出编网法[4][5]，这两种方法都避免了矩阵自乘，因此显得很方便。本文主要采用编网法进行聚类。编网法的主要步骤：（1）通过样本的特征数据，根据实际问题，选择恰当的计算公式计算出；（2）建立相似矩阵的截矩阵 Rλ；（3）选取恰当的λ值进行编网，得出符合要求的分类。 ijr 3. 模糊聚类分析法经济区域划分中的应用 3.1 符号说明（1）对各省市编号北京 1，天津 2，河北 3，山西 4，内蒙 5，辽宁 6，吉林 7，黑龙江 8，上海 9，江苏 10，浙江 11，安徽 12，福建 13，江西 14，山东 15，河南 16，湖北 17，湖南 18，广东 19，广西 20，海南 21，四川 22，贵州 23，云南 24，西藏 25，陕西 26，甘肃 27，青海 28，宁夏 29，新疆 30。（2）对各经济指标进行说明 Y ：GDP，：居民消费水平，：固定资产投资，：职工平均工资，：货 3X 物周转量，：居民消费价格指数，：商品零售价格指数，：工业总产值。： n = （1,2，3，…，30）， m （1,2，…,8）。第个省市的第个经济指标的数值。其中 m = n 7X 4X mnk 1X 5X 2X 6X - 3 -

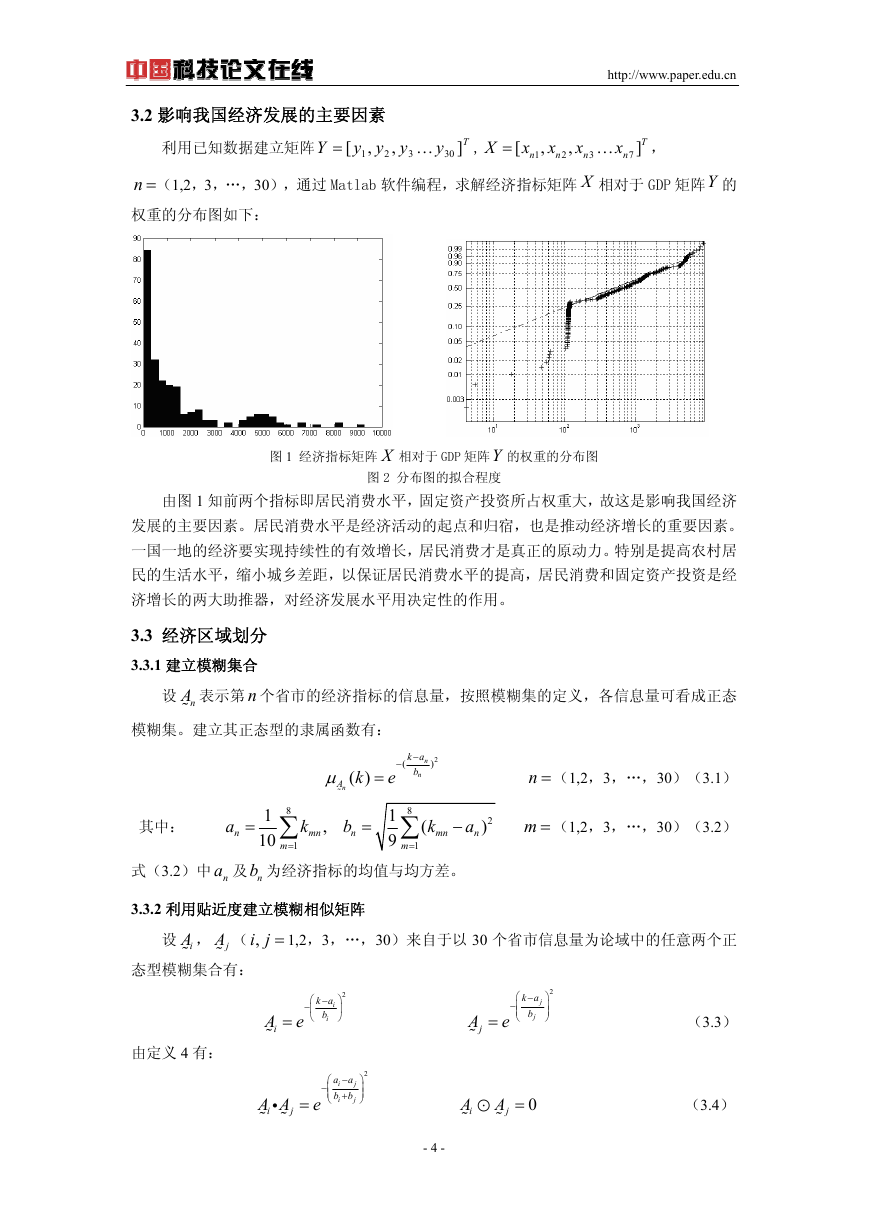
3.2 影响我国经济发展的主要因素 yy 1 利用已知数据建立矩阵 Y = [ , 2 http://www.paper.edu.cn , y 3 … y 30 T ] X , = [ x n 1 , x n 2 , x n 3 … x n 7 ]T ， n =（1,2，3，…，30），通过 Matlab 软件编程，求解经济指标矩阵X 相对于 GDP 矩阵Y 的权重的分布图如下：图 1 经济指标矩阵 X 相对于 GDP 矩阵Y 的权重的分布图图 2 分布图的拟合程度由图 1 知前两个指标即居民消费水平，固定资产投资所占权重大，故这是影响我国经济发展的主要因素。居民消费水平是经济活动的起点和归宿，也是推动经济增长的重要因素。一国一地的经济要实现持续性的有效增长，居民消费才是真正的原动力。特别是提高农村居民的生活水平，缩小城乡差距，以保证居民消费水平的提高，居民消费和固定资产投资是经济增长的两大助推器，对经济发展水平用决定性的作用。 3.3 经济区域划分 3.3.1 建立模糊集合设表示第 n 个省市的经济指标的信息量，按照模糊集的定义，各信息量可看成正态 nA 模糊集。建立其正态型的隶属函数有： − ( k a − n b n 2 ) A k ( ) μ n = e n = （1,2，3，…，30）（3.1）其中： a n 8 ∑ m 1 = k mn , b n = 1 9 8 ∑ m 1 = ( k mn − a n 2 ) m = （1,2，3，…，30）（3.2） = 1 10 nb 式（3.2）中及为经济指标的均值与均方差。 na 3.3.2 利用贴近度建立模糊相似矩阵设，iA ,i jA （态型模糊集合有： j = 1,2，3，…，30）来自于以 30 个省市信息量为论域中的任意两个正 2 ⎛ −⎜ ⎝ k a ⎞− i ⎟ b ⎠ i iA e = j k a − b j 2 ⎞ ⎟ ⎟ ⎠ ⎛ −⎜ ⎜ e ⎝= jA （3.3）由定义 4 有： ⎛ −⎜ ⎜ a a − i b b +⎝= i e i A A i j 2 ⎞ ⎟ ⎟ ⎠ j j A i - 4 - A = j 0 （3.4）

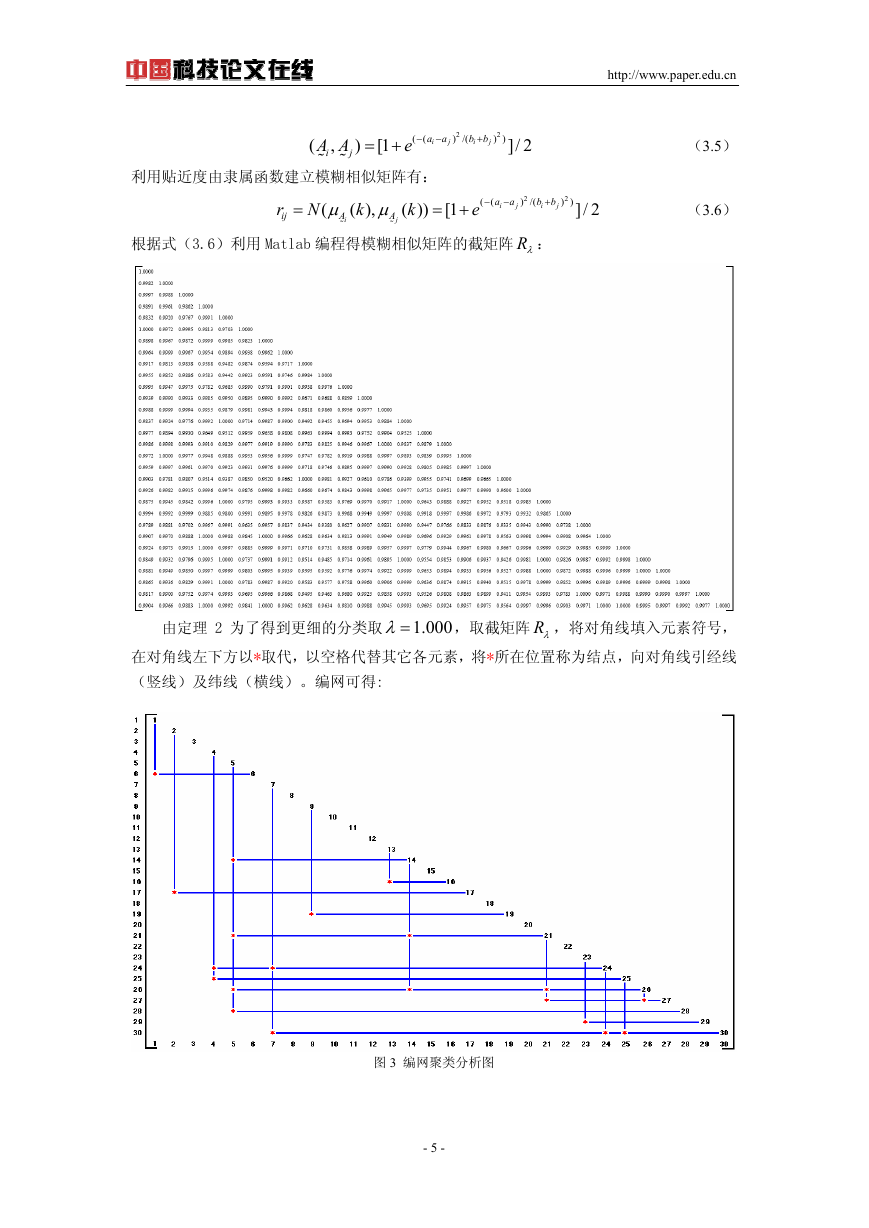
http://www.paper.edu.cn ) [1 = + ( e − j ( a a − i j 2 ) /( b b + i j 2 ) ) ]/ 2 （ 3.5） ( 利用贴近度由隶属函数建立模糊相似矩阵有： , A A i r ij = N k ( ), ( μ μ A A i k ( )) [1 = + e j ( − ( a a − i j 2 ) /( b b + i j 2 ) ) ]/ 2 （3.6）根据式（3.6）利用 Matlab 编程得模糊相似矩阵的截矩阵 Rλ：，取截矩阵 Rλ，将对角线填入元素符号，在对角线左下方以*取代，以空格代替其它各元素，将*所在位置称为结点，向对角线引经线由定理 2 为了得到更细的分类取 000.1=λ （竖线）及纬线（横线）。编网可得: 图 3 编网聚类分析图 - 5 -

3.3.3 分类结果由编网聚类分析图，将经过结点处的经纬线捆绑起来，通过打结而能互相联结的点属于 http://www.paper.edu.cn ∪ {2，17} ∪ ∪ ∪ {9，19} ∪ 同一类，从而得到分类结果：{1，6} {5，14，21，26， {13，16}∪ {23，29}∪ {3，8，10，11，12，15，18，20，22}，即：{北 27，28} 京，辽宁} ∪ {天津，湖北} {内蒙古，江西，海南，陕西，甘肃，青海} ∪ {上海，广东} ∪ {福建，河南} ∪ {贵州，宁夏} ∪ {河北，黑龙江，江 {山西，吉林，云南，西藏，新疆} {4，7，24，25，30} ∪ ∪ 苏，浙江，安徽，山东，湖南，广西，四川}。 3.3.4 分类结果评价显然分类具有意义，第一类，经济发达地区：{上海，广东}；第二类，经济较发达地区： {北京，辽宁}，{天津，湖北}，{河北，黑龙江，江苏，浙江，安徽，山东，湖南，广西，四川}，{福建，河南}；第三类，经济欠发达地区：{山西，吉林，云南，西藏，新疆}，{内蒙古，江西，海南，陕西，甘肃，青海}；第四类，经济贫困地区：{贵州，宁夏}。从以上的模糊聚类分析的结果来看：第一类是上海市和山东省。上海市是我国华东地区的商业大都市，也是我国的经济中心，人均收入和消费水平比较高，交通便利而且气候相当宜人。生产总值比较高，以轻工业为主，兼有部分重工业和物流企业。广东省是我国比较早的进行改革开放的省市之一，经济发展以外资经济为主，包括广州、深圳、湛江等一下港口城市。再加上濒临香港和澳门特别行政区，加强了港澳地区的经济往来。第二类地区是北京，辽宁，天津，湖北、河北、黑龙江、江苏、浙江、安徽、山东、湖南、广西、四川、福建、河南。北京市是我国的首都政治中心，也是人均收入且生活消费水平比较高的地方，但是由于水上运输的不发达和上海市相比具有一定的差距，也算相对发达的地区。辽宁省和黑龙江省是我国的两大重工业基地，用有比较丰富的矿藏资源和丰富的劳动力，使我国工业生产的命脉。天津市位于渤海湾地区，是北京地区的入海口，故而在经济上发展是比较快的。河北、河南、安徽、湖北和湖南省都是我国的内陆省份，交通比较便利，也是我国的人口大省，在经济的发展过程中是比较平稳的水平，位于中等偏上。江苏、浙江、山东、广西、福建都是我国的沿海地区经济比较发达地区，交通优势比较明显，而且对外贸易比较多，但是由于上海和广东省的影响，在经济发展上就相对来说比较差一点，但也算是比较发达的。深处内陆的四川省由于具有丰富的水能资源，且消费水平比较低，所以相对来说人均的生活水平比较高。第三类地区是山西、吉林、云南、西藏、新疆、内蒙古、江西、海南、陕西，甘肃、青海。西部地区的云南、西藏、新疆、内蒙古、陕西、甘肃、青海这些地区由于地理位置不佳，所以说在经济的发展之上是比较滞后的。山西省是我国的产煤大省，但是考虑到其不发达的公路交通运输水平，就导致了铁路单一性的运输方式，经济的发展比较缓慢。吉林省和江西省都属于内陆省份，没有突出的优势，因而相对一般。海南省是沿海城市但是由于开发的不足，工业产值不高，所以相对落后。第四类地区是贵州、宁夏。贵州省隶属我国的西南内陆地区，多为高原地貌，交通运输落后。再加上外出的务工人员比较多，就造成了经济发展水平比较落后。宁夏省的人口比较少，而且在一些地区水资源比较匮乏，土地比较贫瘠，最重要的是多沙漠地带，所以经济的发展历来就是比较落后的。聚类分析的结果与实际情况比较吻合，所以采用模糊聚类分析方法得到的结论是合理、可行的。 - 6 -

http://www.paper.edu.cn 4. 结语（1）居民消费水平是经济活动的起点和归宿，也是推动经济增长的重要因素。特别是提高农村居民的生活水平，缩小城乡差距，以保证居民消费水平的提高。居民消费和固定资产投资是经济增长的两大助推器，对经济发展水平用决定性的作用。（2）经济发展区域划分是一项相当繁琐的工作，但是借助模糊聚类分析会使问题的解决趋于简便化、科学化和准确化。这种方法可以更广泛的应用于区域经济及其相关的领域。参考文献 [1] 王立新，刘华民．模糊聚类法在我国城市内河水质污染分类研究中的应用[J]，内蒙古大学学报(自然科学版)，2004，35(6)：710-715． [2] 田丽，陈俊，吕元锋．模糊聚类法在水环境质量评价中的应用[J]，测控技术，2005，24(5)：69-70． [3] 王云峰，杨冬．模糊聚类分析法在山东区域经济中的应用[J]，山东省农业管理干部学院学报，2006， 22(4)：156-157． [4] 贺仲雄．模糊数学及其应用[M]，天津：天津科学出版社，1982． [5] 王彩华，宋连天．模糊论方法学[M]，北京：中国建筑工业出版社，1988． [6] 范金城，梅长林．数据分析[M]，北京：科学出版社，2002． [7] 胡守信，李柏年．基于 MATLAB 的数学实验[M]，北京：科学出版社，2004． [8] 李士勇．工程模糊数学及应用[M]，哈尔滨：哈尔滨工业大学出版社，2004． [9] 杨纶标，高英仪．模糊数学原理及应用[M]，广州：华南理工大学出版社，2005． Application of Fuzzy Clustering Analysis Method on Classification of Economical Districts 1 Traction Power State Key Laboratory，Southwest Jiaotong University，Chengdu，Sichuan，PRC， Xu Peng1，Yang Jia2，Cai Cheng-biao1 2 School of Traffic Transportation Engineering，Tongji University，Shanghai，PRC， 610031 201804 Abstract This paper is mainly considering a method to classify the economical districts, Using Matlab can help us to draw a conclusion on which factor can demonstrate the predominance in GDP by showing us a figure, and then we can find the factor which is contributing more. Also, the author adopts the theory of fuzzy mathematics to build fuzzy similarity matrices by using approach degree, and the result of classification of economical districts is obtained through making use of net-making method. Keywords: fuzzy clustering analysis；classification of economical districts；fuzzy mathematics； net-making method 作者简介：徐鹏(1985-)，男，湖北潜江人，西南交通大学工学硕士研究生，从事轨道结构参数优化设计研究。 - 7 -

分享到：

赞收藏

资料库

模糊聚类分析法在经济区域划分中的应用.pdf

相关推荐

开发技术

热门标签

最新资料