建立适用于竖向荷载作用下系统识别的斜拉桥简化模型.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：1.05M 资料格式：pdf 举报版权申诉

weixin_38746515-12149029-16359647518123176254.pdf-第1页.png

第1页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第2页.png

第2页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第3页.png

第3页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第4页.png

第4页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第5页.png

第5页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第6页.png

第6页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第7页.png

第7页 / 共12页

weixin_38746515-12149029-16359647518123176254.pdf-第8页.png

第8页 / 共12页

文本预览

中国科技论文在线 http://www.paper.edu.cn 建立适用于竖向荷载作用下系统识别的斜拉桥简化模型# 黄洪葳1，储忻2，孙利民3* （1. 同济大学桥梁工程系，上海市 200092； 2. 里海大学土木与环境工程系，伯利恒市，18015； 3. 土木工程防灾国家重点实验室，上海市 200092）摘要：基于结构动力响应的损伤识别技术是结构健康监测的核心技术之一，其关键问题在于准确和有效地进行结构系统参数识别。目前为止，关于系统识别的数据分析方法已经有很多，但是这些方法通常以自由度小、构成形式简单的结构为研究对象。因此，要使得这些系统识别方法能真正在大型复杂的桥梁结构中得到应用，模型简化是必不可少的环节。本文主要研究如何将多自由度、复杂的桥梁结构简化为便于理论和数值分析的等效模型，针对竖向荷载对结构的作用，建立用于系统识别的斜拉桥简化模型，使其在静力和动力方面与原始全桥模型等效。关键词：斜拉桥；结构健康监测；结构系统识别；简化模型中图分类号：TU997 Establishing simplified model of a cable-stayed bridge for system identification under vertical excitaion HUANG Hongwei1, CHU Xin2, SUN Limin3 (1. Department of Bridge Engineering, Tongji University, Shanghai 200092; 2. Department of Civil and Environmental Engineering, Leigh University, Bethlehem, 18015; 3. State Key Laboratory for Disaster Prevention of Civil Engineering, Shanghai 200092) Abstract: Damage identification based on vibration data is one of the essential technique of Structural Health Monitoring (SHM), the key is to accurately and effectively carry out structural system identification. Although, there are a lot of analysis methodologies available in the literature for system identification, most of them work on either simple structures or structures with small degree-of-freedom (DOF). Therefore, in order to apply these techniques to large and complex bridge structures, model simplification has to be carried out. This paper focuses on how to establish an equivalent model for a complex bridge structure with large DOFs using reasonable simplfication procedures, for the purpose of theoretical analysis and numerical simulation. A simplified model of a cable-stayed bridge will be established for system identification under vertcial excitations. It will be shown that the proposed simplified model is statically and dynamically equivalent to the original prototype model of the bridge. Key words: cable-stayed bridge; structural health monitoring; structural system identification; simplified model 0 引言 5 10 15 20 25 30 35 40 桥梁作为重要的基础结构设施，其安全性、使用性、耐久性以及可持续性一直是社会各界关注的问题。而安装结构健康监测系统，能全面获取桥梁运营状况的信息，以此评估结构的状态，识别结构的损伤，为桥梁养护、维修和管理的决策提供依据，因此成为土木工程领域的研究热点。基于结构动力响应的损伤识别技术是结构健康监测的核心技术之一，其关键问题在于准基金项目：高等学校博士学科点专项科研基金（编号 20100072120004）作者简介：黄洪葳（1976-），女，副研究员，桥梁健康监测与振动控制. E-mail: hongweih@tongji.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 45 确和有效地进行结构系统参数识别。目前为止，关于系统识别的数据分析方法已经有很多，包括傅立叶变化，小波分析，Hilbert-Huang 频谱分析，基于统计学的估计方法，特征值提取方法，损伤定位向量，模糊逻辑，神经网络等。传统的数据分析方法以傅立叶分析为主，产生傅立叶谱。以傅立叶为基础的方法包括进化谱（例如 [1]），小波时频分析（例如 [2]）。然而，Huang 等[3]指出，这些方法对于 50 识别振动信号中包含的物理过程的固有非线性非稳态特征具有局限性，因此提出了 Hilbert-Huang 频谱分析（HHSA），可用于非稳态信号处理，并应用于线性土木结构的分析。然而以上这些频域分析方法只能离线操作。当结构的构件发生损伤，例如裂缝，构件的刚度将明显降低。因此，结构的损伤可以由损伤构件的参数变化反映出来。为了识别结构的参数以及他们的变化，可以用时域分析方法， 55 包括最小二乘法（LSE）（例如 [4]，[5]），扩展卡尔曼滤波（EKF）（例如[6]，[7]），蒙特卡罗滤波（例如[8]）,和时间序列分析（例如[9]）等方法。无论是频域还是时域分析，目前已有的结构损伤识别方法多以自由度小、构成形式简单的结构为对象进行理论推导和研究。然而，要使得这些损伤识别方法能真正在大型复杂的桥梁结构中得到应用，模型简化是必不可少的环节。因此，本文主要研究如何将多自由度、构 60 成形式复杂的桥梁结构，如斜拉桥，等效为便于理论和数值分析的结构形式相对简化的模型，并同时保证桥梁结构的性能和参数。本文以某斜拉桥为工程背景，将该桥的全桥空间有限元模型简化为二有限元模型，以便于进行损伤识别，并对简化模型进行参数修正，保证两模型的静力和动力特性一致。 65 1 斜拉桥等效有限元模型的建立 1.1 全桥有限元模型某斜拉桥全长 610m，主跨长为 332m，两个边跨长分别为 139m，跨径布置为 139m+332m+139m，全宽 35m，采用双塔双索面钢-混凝土组合梁结构。过渡孔单幅宽 15.25m，全宽 32m，采用预应力混凝土简支箱梁结构。主塔为 Π 形钢筋混凝土结构，塔高为 105m。 70 斜拉索采用扇形密索布置，每索面有 64（2×32）根索，采用对称布置，在每半跨的 32 根索中，边跨和主跨各有 16 根。图1 斜拉桥总体布置图 75 采用 ANSYS10.0 建立的全桥有限元模型如图 2 所示。 - 2 - 小乌龟岛芦潮港

中国科技论文在线 http://www.paper.edu.cn 图2 全桥ANSYS有限元模型该模型主梁、主塔采用 beam4 单元，拉索采用 link10 单元。主塔基础处采用六弹簧模 80 型模拟桩基基础与土的相互作用，弹簧采用 combine14 单元。斜拉索通过刚臂与主梁相连。模型相关的几何和材料特性参数如下：主梁分布质量为 17000kg/m ，弹性模量 E=2.1×105MPa，横截面积 A=0.4068m²，惯性矩 I=0.548m4。 1.2 等效模型 85 由于在日常运营中，桥梁的主梁振动以竖向振动为主，所以本文将建立仅考虑竖向荷载作用的二维等效简化模型，各结点的自由度包括竖向和转角位移。由此，斜拉桥主梁可以简化为一根弹性支承连续梁，斜拉索用竖向弹簧代替。根据原设计图，边墩支座中心线设在锚固端两索的中点，故简化模型在此处设竖向支承。由于该斜拉桥是半漂浮体系，在塔墩处主梁下也设竖向支承。简化模型如图 3 和 4 所示： 90 图 3 简化弹性支承连续梁模型（左半跨） 95 图4 尾索区详图 - 3 - 23.57.513523.51089

中国科技论文在线 http://www.paper.edu.cn 由于斜拉索的水平分力作用，主梁承受压力。在现代密索体系斜拉桥中，主梁因斜拉索而承受的压力很大，而且对于截面纤细的主梁，这些压力的作用效应更为显著，故不能忽略。根据结构动力学知识，由于受压构件在受到压力时有屈曲的趋势，必须考虑其几何刚度。在等效模型中，主梁每两个竖向支撑之间划分 1 个单元，故共有 67 个单元。采用一维 100 梁单元，每单元有 2 个节点，每节点有竖向位移和角位移 2 个自由度，如图 5 所示：图5 一维梁单元自由度则单元位移向量为 105 对应的单元总刚度矩阵为 (1) (2) 其中，k 为弹性刚度矩阵，kG 为几何刚度矩阵，E 为单元弹模，I 为截面惯性矩，L 为单元长度，N 为单元所受轴向力。 110 由于假设梁单元质量沿梁长均匀分布，单元质量矩阵采用一致质量矩阵，为 ; (3) (4) 其中，为单元线密度，L 为单元长度。根据有限元理论，将单元刚度矩阵和单元质量矩阵集装成总体刚度矩阵和总体质量矩 115 阵，并将弹簧的刚度直接叠加在总体刚度矩阵中相应自由度位置的主系数上。引入边界条件之后即可获得结构总刚度矩阵 K（132×132），和总质量矩阵 M（132×132）。因为模型共有 67 个单元，所以结构自由度总数为 132。 - 4 - 1122vvvGkkk22322636332326363332LLLLLLEIkLLLLLLL222236336334336336330334GLLLLLLNkLLLLLLL2222156225413224133541315622420133224LLLLLLmLmLLLLLLm

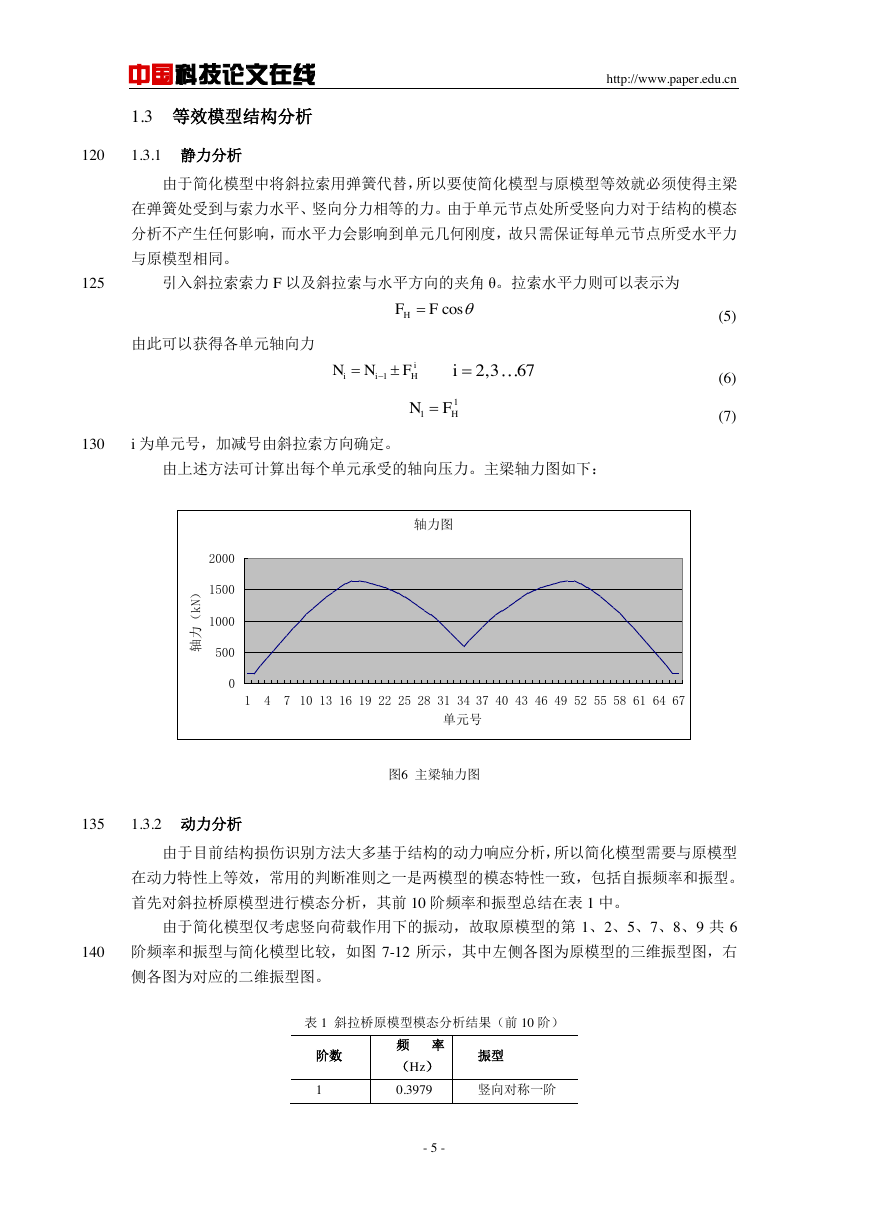
中国科技论文在线 1.3 等效模型结构分析 120 1.3.1 静力分析 http://www.paper.edu.cn 由于简化模型中将斜拉索用弹簧代替，所以要使简化模型与原模型等效就必须使得主梁在弹簧处受到与索力水平、竖向分力相等的力。由于单元节点处所受竖向力对于结构的模态分析不产生任何影响，而水平力会影响到单元几何刚度，故只需保证每单元节点所受水平力与原模型相同。 125 引入斜拉索索力 F 以及斜拉索与水平方向的夹角 θ。拉索水平力则可以表示为由此可以获得各单元轴向力 130 i 为单元号，加减号由斜拉索方向确定。由上述方法可计算出每个单元承受的轴向压力。主梁轴力图如下： (5) (6) (7) 图6 主梁轴力图 135 1.3.2 动力分析由于目前结构损伤识别方法大多基于结构的动力响应分析，所以简化模型需要与原模型在动力特性上等效，常用的判断准则之一是两模型的模态特性一致，包括自振频率和振型。首先对斜拉桥原模型进行模态分析，其前 10 阶频率和振型总结在表 1 中。由于简化模型仅考虑竖向荷载作用下的振动，故取原模型的第 1、2、5、7、8、9 共 6 140 阶频率和振型与简化模型比较，如图 7-12 所示，其中左侧各图为原模型的三维振型图，右侧各图为对应的二维振型图。表 1 斜拉桥原模型模态分析结果（前 10 阶）阶数 1 频率（Hz） 0.3979 振型竖向对称一阶 - 5 - cosHFF1iiiHNNF2,367i11HNF轴力图05001000150020001471013161922252831343740434649525558616467单元号轴力（kN）

中国科技论文在线 http://www.paper.edu.cn 2 3 4 5 6 7 8 9 10 0.5079 0.5405 0.6138 0.8124 1.0118 0.9215 1.032 1.2253 1.2657 竖向反对称一阶横向对称一阶扭转一阶竖向对称二阶扭转一阶竖向反对称二阶竖向对称三阶竖向反对称三阶扭转三阶 145 图7 竖向对称一阶振型图8 竖向反对称一阶振型 - 6 - 150

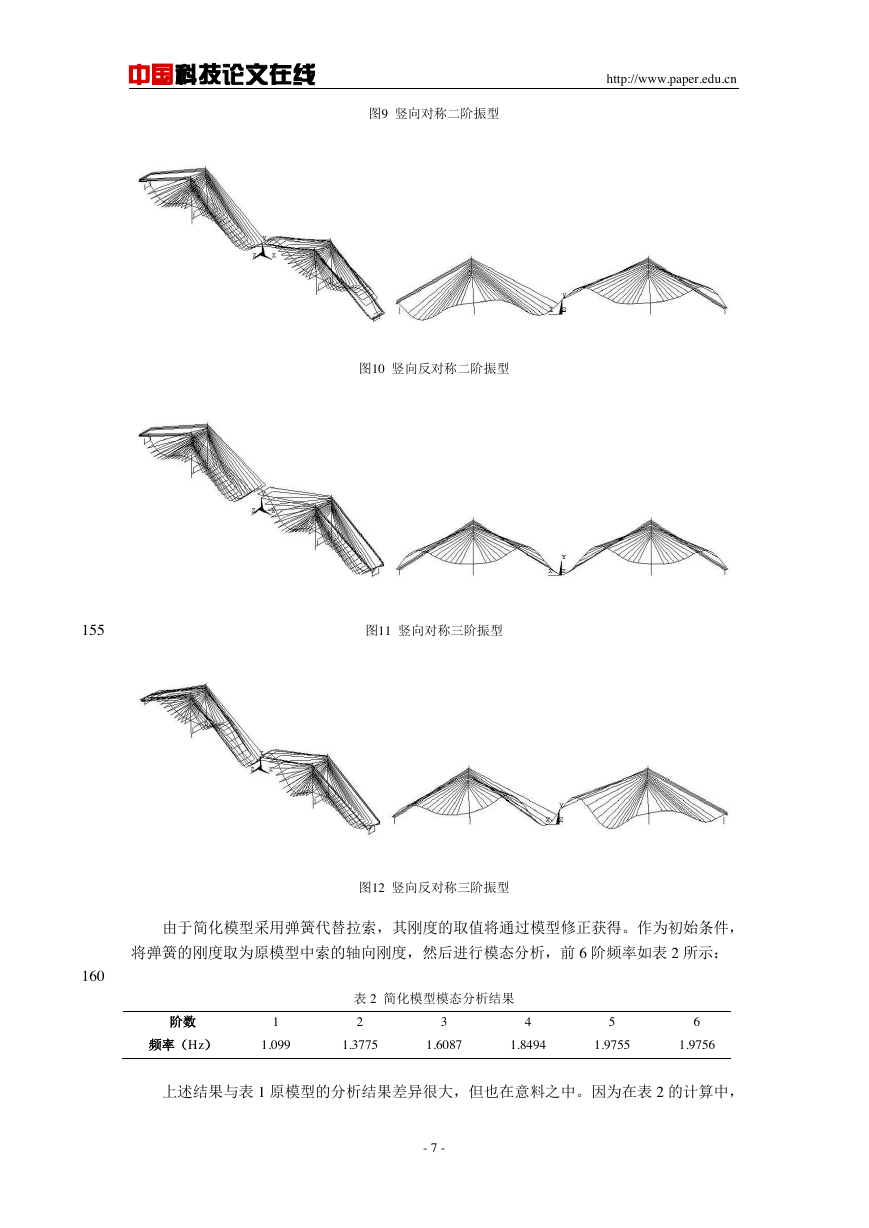
中国科技论文在线 http://www.paper.edu.cn 图9 竖向对称二阶振型图10 竖向反对称二阶振型 155 图11 竖向对称三阶振型图12 竖向反对称三阶振型由于简化模型采用弹簧代替拉索，其刚度的取值将通过模型修正获得。作为初始条件，将弹簧的刚度取为原模型中索的轴向刚度，然后进行模态分析，前 6 阶频率如表 2 所示： 160 表 2 简化模型模态分析结果阶数频率（Hz） 1 2 3 4 5 6 1.099 1.3775 1.6087 1.8494 1.9755 1.9756 上述结果与表 1 原模型的分析结果差异很大，但也在意料之中。因为在表 2 的计算中， - 7 -

中国科技论文在线 http://www.paper.edu.cn 索的刚度 k 是根据理想的轴心受拉构件刚度计算公式计算的，而实际应用中，斜拉索需考虑 165 垂度等几何非线性因素的影响，因此刚度值发生较大变化。所以需要对简化模型进行修正，弹簧的刚度将作为主要被修正的参数。 2 简化模型参数修正模型修正可以通过不同的方法实现，本文将采用应用于青马大桥缩尺模型修正的基于参数敏感度的方法[10]，对所建立的简化模型进行参数修正，使其与原模型动力等效。 170 2.1 基本理论对于一个 n 自由度有限元模型的无阻尼振动，第 i 个特征值i 和相应的阵型i 可以通过解下列的特征值问题求得， (8) 175 通常情况下，结构的刚度矩阵 K 和质量矩阵 M 是结构参数（反映单元几何和材料特性）和边界条件的函数。假设 Pa = {pi,a, i = 1, 2, ... , np}T 为原模型的参数，P = {pi, i = 1, 2, ... , np}T 为修正后的结构参数，a = {i,a, i = 1, 2, ... , na}T 为原模型特征值，e = {i,e, i = 1, 2, ... , ne}T 为简化模型特征值，其中 np 为参数个数，na 为原模型用于修正的模态个数，ne 是简化模型用于修正的模态个数。使原模型与简化模型用于修正的模态个数相等，即 na = ne。 180 简化模型和原模型特征值的函数关系可以用结构参数的一阶泰勒级数展开来近似，即 (9) 其中是特征值残差，=e-a，P 是结构参数的扰动，P = P-Pa = {pi, i = 1, 2, ... , np}T， S 是敏感度矩阵。 185 由此可以设定模型修正的目标函数为转化为矩阵和向量形式，则有 (10) 其约束条件为 190 其中， ; ; ； WE 和 Wp 是权矩阵，bl 和 bu 分别为结构参数残差的上下限。 (11) (12) (13) 最小化式(11)和(12)给出的含约束条件的目标函数，便可求解简化模型的最优参数。有 195 关基于参数敏感度的模型修正方法的具体推导参见[10]. 2.2 初始值设定本文的模型修正目标为保证简化模型和原模型的前 6 阶频率与振型相同，因此待修正的 - 8 - iiiKM=SP()()TTPEJPWPSPWSP1()2TJxxWxAxdPxSPulbdb00IAI00PEWWW

分享到：

赞收藏

资料库

建立适用于竖向荷载作用下系统识别的斜拉桥简化模型.pdf

相关推荐

开发技术

热门标签

最新资料