logo资料库

遗传算法优化神经网络的拓扑结构与权值.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.48M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    2 2 2 第 23卷第 4期 2006年 12月 2 广东工业大学学报 Journa l of Guangdong Un iversity of Technology Vol. 23　No. 4 December 2006 遗传算法优化神经网络的拓扑结构与权值 谷小青 1 ,易当祥 1, 2 ,刘春和 2 (1. 西北工业大学 经济研究中心 ,陕西 西安 , 710072; 2. 北京清河大楼子八 ,北京 , 100085) 摘要 :遗传算法 ( GA )和人工神经网络 (ANN )的相互结合有辅助式和合作式两种方式. 本文在此基 础上提出了融合 、BP_GA和 GA_BP三种算法 ,并采用 GA _BP算法同时优化 BP神经网络的结构 、权 值和阈值 ,研究和实现了一套先进的编码技术和进化策略 ,克服了传统 BP神经网络经验尝试方法 的盲目性. 实例优化与检验结果表明 :遗传算法优化获得的神经网络比由经验尝试法得到的 BP网 络性能更优异 ,方法更合理. 关键词 :遗传算法 :神经网络 ;拓扑结构 ;权值 中图分类号 : TP183　　　　文献标识码 : A　　　　文章编号 : 1007 7162 (2006) 04 0064 06 遗传算法 ( Genetic A lgorithm s,简称 GA ) 和人工神经网络 (A rtincial Neural Network,简称 ANN )是两种重要的计算智能技术 , ANN 计算速度快 ,局部寻优能力强 ,但易于陷入局部极小 ; GA则具有其他算法所没有的自适应性 、全局优化性和隐含并行性 ,但局部寻优能力不强 [ 1 2 ]. 怎么将两种优势互补的 GA与 ANN 相互结合起来正成为一个研究热点. GA 与 ANN 的结合主 要表现为两种方式 :一种是辅助式结合 ,比较典型的是利用 GA对数据进行预处理 ,然后用 ANN 求解问题 [ 3 ] ,比如在模式识别中先利用 GA 进行特征提取 ,而后用 ANN 进行分类 ;另一种是合 作式结合 ,即 GA和 ANN共同求解问题 ,主要集中在网络的权值与门阈值及网络结构的优化方 面 [ 4 6 ]. 1　GA 与 BP的混合模型 在合作式结合的模型中 , GA 优化 BP,可以提高神经网络的泛化能 力 、收敛能力和求解精度. 但 GA 和 BP的结合算法却是多样的 ,优化的 对象也并不完全相同 ,不仅可以优化权值和阈值 ,也可以优化网络结构 和训练规则 ;而且不同的结合模型其收敛精度和搜索时间也不一样. 1. 1　融合算法 融合算法如图 1所示. 其主要步骤为 :首先随机产生初始个体群 ,然 后进行迭代 ,每次迭代首先进行遗传操作 ,并选择出子代精英和相应的 父代个体组成训练模式 ,然后进行 BP网络训练 ,并记忆 BP网络操作得 出的映射关系 ;若 BP训练成功 ,则由 GA 产生少量个体 , BP中抽取多个 个体 ,若 BP训练不成功 ,则由 GA 产生多个个体 , BP网中抽取少数个 体 ,最后在满足终止条件时结束算法. 从融合角度讲 ,本算法结合了 BP的学习能力和 GA 的进 图 1　融合算法流程图 收稿日期 : 2006 作者简介 :谷小青 (1978 11 09 ) ,女 ,博士生 ,主要研究方向为系统工程 、优化设计等.
    第 4期 谷小青 ,等 :遗传算法优化神经网络的拓扑结构与权值 56 化能力 ,使个体边学习边进化 ,这更符合生物成长的实际特点. 1. 2　GA _BP算法 该算法先用 GA反复优化神经网络的权值 ,直到平均值不再有意义地增加为止. 此时解码 得到的参数组合已经充分接近最佳参数组合 ,在此基础上 ,再用 BP算法对它们进行局部优化 , 这种方法的通用性较好. GA _BP算法如图 2所示. 1. 3　BP_GA算法 BP_GA 算法如图 3 所示. 先产生 多个初始值 ,这些初始值中有一部分 用固定用 BP算法来优化 ,另外一部分 固定用 CA来优化 ,其分配的比例可事 先给出 ,以此计算 ,直到最终的结果达 到指定的误差范围. 2 　神经网络结构和权值的 优化设计 对于 BP神经网络的易陷入局部 图 2　GA _BP算法流程图 　　图 3　BP_GA算法流程图 最小的缺点 ,有一些改进算法 ,如改进的梯度下降搜索法 、模拟退火法和遗传算法 [ 7 ]. 但它们解 决的仅仅是 BP网络如何收敛最快并如何跳出局部极小点的问题 ,并得到某种网络结构的权值 矩阵和门阀值矩阵. 但对于神经网络的结构设计大多数都是根据经验或尝试的办法 ,确定神经 网络的层数 、节点数 、算法 、参数及初始值. 本文将神经网络的结构设计和权值设计一起优化 ,通 过训练得到更优和更合理的 BP网络. 由 BP网络映射能力的完全性定理可知 ,如果网络中隐含层节点可以根据需要自由设定 , 那么一个三层网络可以完全实现以任意精度近似任何连续函数. 一般地 ,三层网络的输入输出 节点数是根据求解问题确定的 ,只有隐含层节点数是可变的 ,它的个数是神经网络结构优化的 对象. 隐含层单元数太少 ,网络可能训练不出满意结果 ,或者网络不强壮 ,容错性差 ;隐含层单元 数太多 ,会使学习时间过长 ,误差也不一定最小 ,因此存在一个最佳的隐层单元数. 假设网络是严格分层全连接的 ,即当且仅当两相邻层的结点才有可能进行连接 ,且必须有 连接 ,每一神经元都设成是线性阈值单元且使用 sigmoid传递函数 :输入输出空间向量在实数空 间上取值 ,相连接的两个神经元如果没有影响 ,则权值为 0. 那么在输入和输出层节点数已知的 前提下 ,权值的个数就可以和隐含层节点数唯一对应起来. 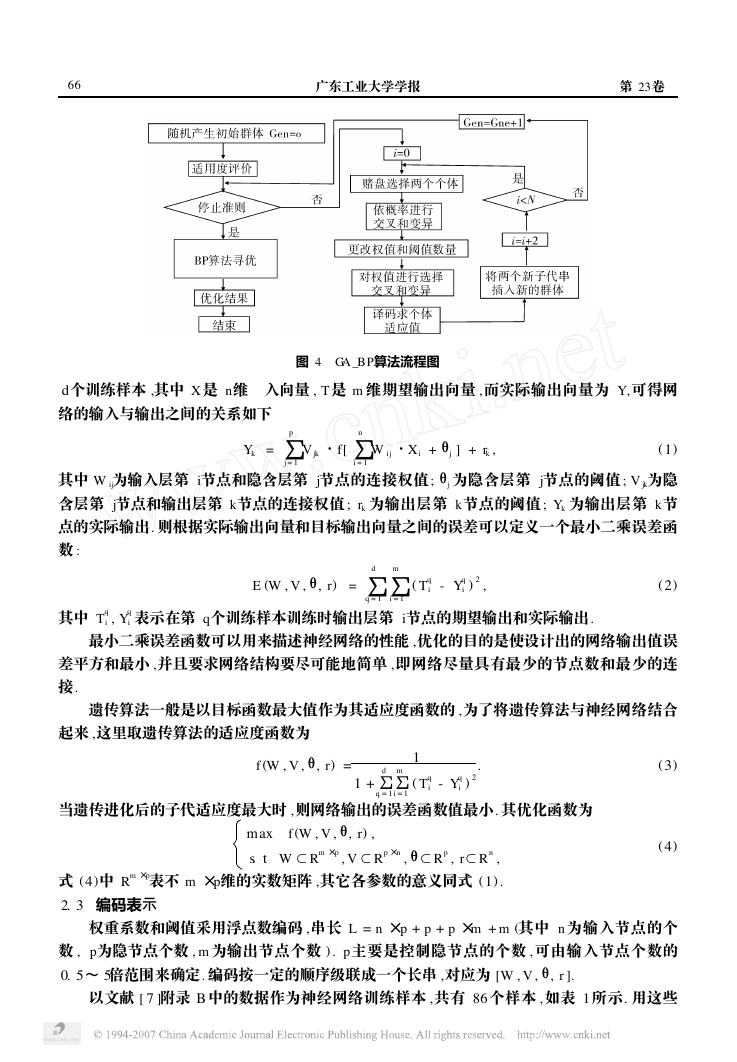2. 1　 GA _BP算法流程 以上面的 GA _BP算法作为模式 ,先用 GA 优化权值及其个数 ,得到一个全局较优的解 ,然 后将最后一代得到的个体解码 ,得到相应的 BP网络结构和权值及阀值. 并将这些值作为 BP网 络结构和初值 ,用样本训练来进一步局部的精确寻优 ,求出最优的权值利结构 ,如图 4所示. 2. 2　进化策略 p 对 n m 三层 BP神经网络 , n为输入节点数 , p为隐节点数 , m 为输出节点数. 其中输入层 到隐含层的激活函数采用 Sigmoid型 ,隐层到输出层的激活函数采用线性函数. 给定一个训练 集 ,其输入模式为 [ X1 , X2 , …, Xq , …, Xd ],对应的目标输出为 [ T1 , T2 , …, Tq , …, Td ],表示共有
    66 广东工业大学学报 第 23卷 d个训练样本 ,其中 X是 n维 　入向量 , T是 m 维期望输出向量 , 而实际输出向量为 Y, 可得网 络的输入与输出之间的关系如下 图 4　GA _BP算法流程图 Yk = ∑ V jk ·f [ ∑ W ij ·Xi +θj ] + rk , p j = 1 n i = 1 ( 1) 其中 W ij为输入层第 i节点和隐含层第 j节点的连接权值 ;θj 为隐含层第 j节点的阈值 ; V jk为隐 含层第 j节点和输出层第 k节点的连接权值 ; rk 为输出层第 k节点的阈值 ; Yk 为输出层第 k节 点的实际输出. 则根据实际输出向量和目标输出向量之间的误差可以定义一个最小二乘误差函 数 : E (W , V,θ, r) = ∑ ∑ ( Tq i q = 1 i =1 d m - Yq i ) 2 , ( 2) 其中 Tq i , Yq i 表示在第 q个训练样本训练时输出层第 i节点的期望输出和实际输出. 最小二乘误差函数可以用来描述神经网络的性能 ,优化的目的是使设计出的网络输出值误 差平方和最小 ,并且要求网络结构要尽可能地简单 , 即网络尽量具有最少的节点数和最少的连 接. 遗传算法一般是以目标函数最大值作为其适应度函数的 ,为了将遗传算法与神经网络结合 起来 ,这里取遗传算法的适应度函数为 f (W , V,θ, r) = 1 ( Tq i - Yq i ) 2 . d 1 + ∑ q = 1 m ∑ i = 1 当遗传进化后的子代适应度最大时 ,则网络输出的误差函数值最小. 其优化函数为 max　f (W , V,θ, r) , s. t　W Rm ×p , V Rn , 式 (4)中 Rm ×p表不 m ×p维的实数矩阵 ,其它各参数的意义同式 ( 1) . 2. 3　编码表示 Rp , r Rp ×n ,θ ( 3) ( 4) 权重系数和阈值采用浮点数编码 ,串长 L = n ×p + p + p ×m + m (其中 n 为输入节点的个 数 , p为隐节点个数 , m 为输出节点个数 ) . p主要是控制隐节点的个数 , 可由输入节点个数的 0. 5～ 5倍范围来确定. 编码按一定的顺序级联成一个长串 ,对应为 [W , V,θ, r ]. 以文献 [ 7 ]附录 B 中的数据作为神经网络训练样本 ,共有 86个样本 , 如表 1所示. 用这些
    第 4期 谷小青 ,等 :遗传算法优化神经网络的拓扑结构与权值 样本数据来研究遗传算法优化神经网络的方法和检验优化后神经网络的性能 : i- 1 D i = f (σi , ∑ D k ) , k = 1 /4 76 ( 5) 式中 D i 为第 i个载荷循环所造成的单次疲劳损伤 ;σi 为第 i个循环应力水平 ; ∑ ∑D ) 为第 i个循环应力水平之前的疲劳累积损伤. k = 1 /4 i- 1 D k (简记为 由上面的分析可知 BP网络的输入节点为 2,输出节点为 1. 设隐层节点数为 s,在 1～10范 围内取值 ,则可假定神经网络的拓扑结构为 2 - s - 1三层 BP网络 ,如图 5所示. 若 s是需要确定的隐含层节点数 ,则串长 L = 4s + 1, 确定了 L 的长度就可以确定网络节点 数 ,其个体解码值就是分别对应的权值和阈值. 对图 5的 2 - s - 1网络按编码程序其串码如下 W 3, 1 , W 3, 2 , …, W 2 + i, 1, W 2 + j, 2 , …, W 2 + s, 1 , W 2 + s, 2 , W 3 + s, 3 , …, W 3 + s, 2 + j, …, W 3 + s2 + s , b3 , …b2 + j, …, b2 + s , b3 + s , 其中 W 为神经网络权值 , b为阈值. 表 1　BP网络训练样本 序号 应力级 σ/MPa累积损伤 ∑D 单次损伤 D 1 2 3 ⁝ 83 84 85 86 410 410 410 ⁝ 390 390 390 390 0 0 0 0 0 0 0 000 006 2 000 318 6 000 670 2 ⁝ 559 242 0 692 532 1 815 285 7 999 999 5 0 0 0 0 0 0 0 000 006 2 000 006 8 000 007 3 ⁝ 000 007 1 000 006 2 000 006 1 000 006 2 2. 4　交叉算于和变异算子 图 5　网络拓扑结构 设染色体串长为 L,采用两点交叉算子 ,首先产生两个在 1到 L - 1之间的不同的一致随机 数 ,然后在两个父代中交叉变换. 001 | 0111 | 001→0011001001, 100 | 1001 | 100→ 1000111100. 变异算子在每个串上一般以一个很小的概率发生 , 如果染色体基因为 1, 则该基因变为 0, 反之由 0变为 1. 3　GA _BP仿真试验 σ’= 0 1 ×lg (σ ×106 ) - 0 以表 1中训练样本为学习任务 ,为了更快收敛 ,对训练样本等效变换 1 ×lg ( ∑D ) + 0 ( 6) 在等效处理后的数据中选取 76个样本进行训练 , 另外 10个样本用于检验网络的性能. 当 误差平方和达到预定的目标值或者预先确定的进化代数时 ,就停止训练. 设置如下参数 :变异算 子为 0. 005;交叉算子为 0. 90;种群大小为 30;最大进化代数为 150;最优 ANN 个体训练步数为 100 000. 遗传算法在优化神经网络权值和阈值的过程中 , 随进化代数的增加 , 其适应度收敛情 况如图 6所示 ,逐渐趋于稳定并达到最大值 ,由式 ( 3)可知神经网络的误差平方和最小的 ,此时 1, ∑D ’= 0 9.
    86 广东工业大学学报 第 23卷 神经网络对应的权值和阈值是最优的. 最后 由 GA _BP算法获得满足要求的最优个体为 : - 463 118 2, 24. 569 7, 639. 178 7, - 19. 902 5, 725. 024 2, 24. 661 8, - 597. 407 5, 17. 788 7, - 12. 746, 773. 223 1, 8. 339 3, 684. 860 4, 742. 060 2, 9. 834 3, 351. 823 5, - 483. 257 1, - 578. 407 4, 442. 830 6, - 513. 357, - 595. 937 2, - 1. 476 8, - 571. 100 8, 1. 874 6, - 0. 074 6, 0. 133 1, - 0. 033 3, - 0. 030 2, 0. 105 9, 0. 004 9. 共 29个参数 , 则可求得隐含节点数 为 7,即 BP网络拓扑结构为 2 - 7 - 1,最后面 8个数为阈值. 4　GA _BP网络的检验与比较 为了鉴定优化后的神经网络的性能优劣 ,可以 图 6　平均适应度与最优适应度的收敛曲线 8 7 1网络的仿真结果与疲劳实验的真实值及 用此 2 文献 [ 7 ]的 2 1BP网络的仿真值来比较. 文献 [ 7 ] 通过多次尝试和反复比较 , 认为较优的网络结构是 采用 8个隐含节点的三层网络. 真实值与两种神经网 络仿真值的比较结果如图 7所示 ,其中虚线代表的是 真实值. 由图 7的仿真值和表 2的绝对误差比较 , 可 以明显看出 ,经遗传算法优化出来的 2 1三层网络 和真实值吻合得很好 ,总体上比 2 1网络更接近真 实值 ,性能更优异. 7 8 图 7　网络仿真值比较 表 2　神经网络仿真值与真实值的绝对误差比较 2 - 8 - 1网络绝对误差 0 022 2 0 017 8 0 018 4 0 091 2 0 023 5 0 047 6 0 039 1 0 050 0 0 033 4 0 031 7 2 - 7 - 1网络绝对误差 0 011 9 0 001 7 0 011 9 0 070 2 0 010 5 0 010 3 0 041 2 0 001 4 0 043 2 0 003 3 5　结论 对遗传算法与神经网络的混合模型提出了融合 、BP_GA 和 GA _BP三种算法. 采用其中的 GA _BP算法 ,巧妙合理地将神经网络的误差函数与适应度函数结合起来 , 构建了优化目标函 数 ,来同时优化 BP神经网络的拓扑结构 、权值和阈值. 并研究了一套先进的编码技术和进化策 略 ,遗传算法优化后的神经网络克服了由于传统神经网络拓扑结构和初始权值确定过程中的随 意性所带来的网络振荡 ,也避免了网络易陷入局部解的缺陷. 仿真结果的检验与比较也表明 ,该 优化方法是合理的和可行的.
    第 4期 谷小青 ,等 :遗传算法优化神经网络的拓扑结构与权值 96 参考文献 : [ 1 ]朱大奇. 人工神经网络研究现状及其展望 [ J ]. 江南大学学报. 2004, 3 (1) : 103 [ 2 ]王小平 ,曹立胡. 遗传算法 ———理论 、应用与软件实现 [M ]. 西安 :西安交通大学出版社. 2002. [ 3 ] Eric I Chang, R ichard P L ippmann. U sing genetic algorithm s to imp rove pattern classification performance. Pro ceedings of the 1990 Conference on advances in neural information p rocessing system s 3 [ C ]. Denver, Colorado, U nited States. 797 110. 803. [ 4 ] Yao X. A review of evolutionary artificial neural networks[ J ]. International Journal of Intelligent System s. 1993, 8 (4) : 539 567. [ 5 ]赖鑫生. 神经网络结合遗传算法优化应用 [ J ]. 贵州大学学报. 2004, 21 (2) : 179 [ 6 ]赵正佳 ,黄洪钟 ,陈新. 优化设计求解的遗传神经网络新算法研究 [ J ]. 西南交通大学学报 , 2000, 35 ( 1) : 65 184. 68. [ 7 ]郭浩. 疲劳可靠性分析计算机仿真方法研究 [D ]. 沈阳 :东北大学机械工程与自动化学院. 1999. O ptim iza tion of Topolog ica l Structure and W e ight Va lue of Artif ic ia l Neura l Network Using Genetic A lgor ithm GU Xiao qing1 , YI Dang xiang1, 2 , L IU Chun he2 (1 Econom ics Research Center, Northwestern Polytechnical University, Xi ’an 710072, China; 2 Q ing he Building D8, Beijing 100085, China) GA algorithm and GA Abstract: In crder to make use of the respective advantages of Genetic A lgorithm ( GA ) and BP neural network , integrated algorithm , BP BP algorithm are brought for ward. Genetic algorithm is used to op tim ize the topological structure , the weight values and the biases of BP neural network. Furthermore, a set of advanced coding technique and evolution tactic are studied and realized to overcome the blindness resulted from experiences and tries of traditional BP network. The simulation results of instances show that op tim ised metwork is of better fitting capability and of more reasonable method than traditional BP network. Key words: genetic algorithm; artificial neural network; topological structure; weight value
    分享到：
    赞 收藏

    相关推荐

    资料库

    网络技术

    共收录2367份资料，累计7个分类，关注成员有19位，主要包括：综合布线,网管软件,网络监控,网络设备,其它,系统集成,网络基础

    热门标签

    综合布线 网管软件 网络监控 网络设备 其它 系统集成 网络基础

    最新资料