Introduction to Automata Theory, Languages, and Computation(Seco....doc

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.61M 资料格式：doc 举报版权申诉

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第1页.png

第1页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第2页.png

第2页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第3页.png

第3页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第4页.png

第4页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第5页.png

第5页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第6页.png

第6页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第7页.png

第7页 / 共66页

huangjunhimilyhuang-1428794-4744300845176259206.doc.pdf-第8页.png

第8页 / 共66页

Solutions for Section 2.2

Exercise 2.2.1(a)

Exercise 2.2.2

Exercise 2.2.4(a)

Exercise 2.2.6(a)

Exercise 2.2.9

Exercise 2.2.10

Solutions for Section 2.3

Exercise 2.3.1

Exercise 2.3.4(a)

Solutions for Section 2.4

Exercise 2.4.1(a)

Exercise 2.4.2(a)

Solutions for Section 2.5

Exercise 2.5.1

Solutions for Section 3.1

Exercise 3.1.1(a)

Exercise 3.1.2(a)

Exercise 3.1.4(a)

Exercise 3.1.5

Solutions for Section 3.2

Exercise 3.2.1

Exercise 3.2.4(a)

利用定理3。7每个用正则表达式来定义的语言也可用穷自动机来定义

Exercise 3.2.6(a)

Exercise 3.2.6(b)

Exercise 3.2.8

Solutions for Section 3.4

Exercise 3.4.1(a)

Exercise 3.4.1(f)

Exercise 3.4.2(a)

Exercise 3.4.2(c)

Solutions for Section 4.1

Exercise 4.1.1(c)

Exercise 4.1.2(a)

Exercise 4.1.4(a)

Exercise 4.1.4(b)

Exercise 4.1.4(c)

Solutions for Section 4.2

Exercise 4.2.1(a)

Exercise 4.2.1(c)

正则表达式语言a(ab)*ba

Exercise 4.2.1(e)

Exercise 4.2.5(b)

Exercise 4.2.5(e)

Exercise 4.2.5(f)

Exercise 4.2.8

Exercise 4.2.13(a)

Exercise 4.2.14(c)

Solutions for Section 4.3

Exercise 4.3.1

Solutions for Section 4.4

Exercise 4.4.1

Solutions for Section 5.1

Exercise 5.1.1(a)

Exercise 5.1.1(b)

Exercise 5.1.2(a)

Exercise 5.1.5

Solutions for Section 5.2

Exercise 5.2.1(a)

Exercise 5.2.1(a){ Exercise 5.1.1(a)的语法分析树}

Solutions for Section 5.3

Exercise 5.3.2

Exercise 5.3.4(a)

Solutions for Section 5.4

Exercise 5.4.1

Exercise 5.4.3

Exercise 5.4.6

Solutions for Section 6.1

Exercise 6.1.1(a)

Solutions for Section 6.2

Exercise 6.2.1(a)

Exercise 6.2.2(a)

Exercise 6.2.4

Exercise 6.2.5(a)

Exercise 6.2.8

Solutions for Section 6.3

Exercise 6.3.1

Exercise 6.3.3

Exercise 6.3.6

Solutions for Section 6.4

Exercise 6.4.1(b)

Exercise 6.4.3(a)

Exercise 6.4.3(c)

Solutions for Section 7.1

Exercise 7.1.1

Exercise 7.1.2

Exercise 7.1.10

【没讲】Exercise 7.1.11(b)

【没讲】Exercise 7.1.11(d)

Solutions for Section 7.2

Exercise 7.2.1(a)

Exercise 7.2.1(d)

Exercise 7.2.2(b)

Exercise 7.2.2(c)

Exercise 7.2.4

Solutions for Section 7.3

Exercise 7.3.1(a)

Exercise 7.3.1(b)

Exercise 7.3.3(a)

Exercise 7.3.4(b)

Exercise 7.3.4(c)

Exercise 7.3.5

Solutions for Section 7.4

Exercise 7.4.1(a)

Exercise 7.4.3(a)

Exercise 7.4.4

Solutions for Section 8.1

Exercise 8.1.1(a)

Solutions for Section 8.2

Exercise 8.2.1(a)

Exercise 8.2.2(a)

Exercise 8.2.4

Exercise 8.2.5(a)

Solutions for Section 8.3

Exercise 8.3.3

Solutions for Section 8.4

Exercise 8.4.2(a)

Exercise 8.4.3(a)

Exercise 8.4.5

Exercise 8.4.8(a)

Exercise 8.4.8(a)(?不知所云)

Exercise 8.4.8(b)

Solutions for Section 8.5

Exercise 8.5.1(c)

Exercise 8.5.1(c)(计数器机器P244页，PPT中没有，也没讲)

Solutions for Section 9.1

Exercise 9.1.1(a)

Exercise 9.1.3(a)

Solutions for Section 9.2

Exercise 9.2.2(a)

Exercise 9.2.3(a)

Exercise 9.2.4

Exercise 9.2.5

Exercise 9.2.6(a)

Exercise 9.2.6(e)

Solutions for Section 9.3

Exercise 9.3.1

Exercise 9.3.4(d)

Exercise 9.3.6(a)

Exercise 9.3.7(a)

Exercise 9.3.8(a)

Exercise 9.3.8(d)

Solutions for Section 9.4

Exercise 9.4.1(a)

Exercise 9.4.3

Solutions for Section 9.5

Exercise 9.5.1

Exercise 8.1.1(a)（参考P219-220例8.1，注意归约的方向）We need

Exercise 8.2.1(a)

Exercise 8.2.2(a)

(注意与P224例8.2中0n1n的区别)Here is the transition table

Exercise 8.2.4

Exercise 8.2.5(a)

Exercise 8.3.3

Exercise 8.4.2(a)

Exercise 8.4.3(a)

Exercise 8.4.5

Exercise 8.4.8(a)(?)

Exercise 8.4.8(b)

Exercise 8.5.1(c)(计数器机器P244页，PPT中没有，也没讲)

Exercise 9.1.1(a)

Exercise 9.1.3(a)

Exercise 9.2.2(a)

Exercise 9.2.3(a)

Exercise 9.2.4

Exercise 9.2.5

Exercise 9.2.6(a)

Exercise 9.2.6(e)

Solutions for Section 2.2 Exercise 2.2.1(a) States correspond to the eight combinations of switch positions, and also must indicate whether the previous roll came out at D, i.e., whether the previous input was accepted. Let 0 represent a position to the left (as in the diagram) and 1 a position to the right. Each state can be represented by a sequence of three 0's or 1's, representing the directions of the three switches, in order from left to right. We follow these three bits by either a indicating it is an accepting state or r, indicating rejection. Of the 16 possible states, it turns out that only 13 are accessible from the initial state, 000r. Here is the transition table: 杠杆可能出现 8 种情况，影响着最终状态。并且也要说明，前面一个大理石球是否从 D 滚出，也就是说，前一个输入是否被接受。令 0 代表向左方的状态（如图表）， 1 代表向右方。这三个杠杆的每一个状态都可以用三个数（0 或 1）组成的序列表示。这个序列后面跟着字母 a 或者 r。a 代表接受状态，r 代表拒绝状态。16 种可能的状态中，只有 13 种是从初始状态 000r 可达的。下面它的有穷自动机的转移表。 A B ->000r 100r 011r *000a 100r 011r *001a 101r 000a 010r 110r 001a *010a 110r 001a 011r 111r 010a 100r 010r 111r *100a 010r 111r 101r 011r 100a *101a 011r 100a 110r 000a 101a *110a 000a 101a 111r 001a 110a Exercise 2.2.2 The statement to be proved is δ-hat(q,xy)=δ-hat(δ-hat(q,x),y), and we proceed by induction on the length of y. 证明：通过对|y|进行归纳，来证明ˆ (q , xy)=ˆ (ˆ (q , x) , y) ，具体过程如下： 1

Basis: If y=ε, then the statement is δ-hat(q,x)=δ-hat(δ-hat(q,x),ε). This statement follows from the basis in the definition of δ-hat. Note that in applying this definition, we must treat δ-hat(q,x)as if it were just a state, say p. Then, the statement to be proved is p =δ-hat(p,ε), which is easy to recognize as the basis in the definition of δ-hat. 基础: y =0，则 y=ε。那么需证ˆ (q,x)=ˆ (ˆ (q ,x),ε)，记 p=ˆ (q,x),命题变为 p=ˆ (p ,ε), 由ˆ 的定义知这显然成立。 Induction: Assume the statement for strings shorter than y, and break y=za, where ais the last symbol of y. The steps converting δ-hat(δ-hat(q,x),y)to δ-hat(q,xy) are summarized in the following table: 归纳: 假设命题对于比 y 短的串成立, 且 y=za, 其中 a 是 y的结尾符号。ˆ (ˆ (q,x),y) 到ˆ (q,xy) 的变换总结在下表中: Expression 表达式 Reason 原因 ˆ (ˆ (q,x),y) Start 开始 ˆ (ˆ (q,x),za) y=za by assumption 由假设 y=za δ(ˆ (ˆ (q,x),z),a) Definition of δ-hat, treating δ-hat(q,x) as a state ˆ 的定义, 把ˆ (q,x) 看作是一个状态 δ(ˆ (q,xz),a) Inductive hypothesis 归纳假设 Definition of δ-hat ˆ 的定义 y=za ˆ (q,xza) ˆ (q,xy) Exercise 2.2.4(a) The intuitive meanings of states A, B, and C are that the string seen so far ends in 0, 1, or at least 2 zeros. 状态 A, B，C 分别表示以１,０和 00 结尾的串的状态。 0 1 2

->A B A B C A *C C A Exercise 2.2.6(a) The trick is to realize that reading another bit either multiplies the number seen so far by 2 (if it is a 0), or multiplies by 2 and then adds 1 (if it is a 1). We don't need to remember the entire number seen --- just its remainder when divided by 5. That is, if we have any number of the form 5a+b, where b is the remainder, between 0 and 4, then 2(5a+b) = 10a+2b. Since 10a is surely divisible by 5, the remainder of 10a+2b is the same as the remainder of 2b when divided by 5. Since b, is 0, 1, 2, 3, or 4, we can tabulate the answers easily. The same idea holds if we want to consider what happens to 5a+b if we multiply by 2 and add 1. 对于一个二进制整数，如果读入一个比特０，其值等于原数乘以２；否则等于原数乘以２再加以 1。而任意一个数均可写成形如 5a+b，其中 a 任意，0<= b <=4，那么输入 0，原数变为 2(5a+b) = 10a+2b，由于 10a 是 5 的倍数,，因此 10a+2b 除以５的余数与 2b 相同。输入 1，则得 2(5a+b)+1 类似。因此对于所有的数只要记住它被５除的余数就可以。由于 b是 0, 1, 2, 3 或者 4, 我们可以容易得到该 DPA 的转移表，具体如下： The table below shows this automaton. State qimeans that the input seen so far has remainder i when divided by 5. 其中状态 qi 代表输入串被５除的余数 i 的状态。 0 1 ->*q0 q0 q1 q1 q2 q3 q2 q4 q0 q3 q1 q2 q4 q3 q4 There is a small matter, however, that this automaton accepts strings with leading 0's. Since the problem calls for accepting only those strings that begin with 1, we need an additional state s, the start state, and an additional ``dead state'' d. If, in state s, we see a 1 first, we act like q0; i.e., we go to state q1. However, if the first input is 0, we should never accept, so we go to state d, which we never leave. The complete automaton is: 但是上述自动机仍接受以０开头的字符串。因为题目要求只接受以１开头的串，可增加一个初始状态 s和“死亡状态”d。在状态初始状态 s, 若看到１，则转到状态 q1；若看到０, 则直接转到状态 d，识别终止。所求自动机如下: 3

0 1 ->s d q1 *q0 q0 q1 q1 q2 q3 q2 q4 q0 q3 q1 q2 q4 q3 q4 d d d Exercise 2.2.9 Part (a) is an easy induction on the length of w, starting at length 1. Basis: |w| = 1. Then δ-hat(q0,w)=δ-hat(qf,w), because w is a single symbol, and δ-hat agrees with δ on single symbols. Induction: Let w=za, so the inductive hypothesis applies to z. Then δ-hat(q0,w) = δ-hat(q0,za) = δ(δ-hat(q0,z),a) = δ(δ-hat(qf,z),a) [by the inductive hypothesis] = δ-hat(qf,za) = δ-hat(qf,w). 证明：a) 通过对 w 长度的归纳证明。基础: 若|w| = 1，则 w 是一个符号，此时需证ˆ (q0,w)= ˆ (qf,w), 而对于单个符号扩展转移函数ˆ 与转移函数δ的作用是一样的，得证。归纳: 令 w= za, 假设对于 z 命题ˆ (q0,z) = ˆ (qf,z)成立。那么ˆ (q0,w)= ˆ (q0,za)= δ(ˆ (q0,z),a) = δ(ˆ (qf,z),a) [由归纳假设] = ˆ (qf,za) = ˆ (qf,w). For part (b), we know that δ-hat(q0,x) = qf. Since xε, we know by part (a) that δ-hat(qf,x) = qf. It is then a simple induction on k to show that δ-hat(q0,xk) = qf. Basis: For k=1 the statement is given. Induction: Assume the statement for k-1; i.e., δ-hat(q0,xSUP>k-1) = qf. Using Exercise 2.2.2, δ-hat(q0,xk) = δ-hat(δ-hat(q0,xk-1),x) = δ-hat(qf,x) [by the inductive hypothesis] = qf [by (a)]. 4

b) x 是属于 L(A)的非空串，也即串 x 被接收，因此ˆ (q0,x) = qf ，则由 a)知ˆ (qf,x) =ˆ (q0,x)= qf 。现在通过对 k 的归纳来证明ˆ (q0,xk) = qf 。基础: k=1 时，需证ˆ (q0,x) = qf ，由已知可得。归纳：假设对于 k-1 命题成立，也就是说，ˆ (q0,xk-1) = qf 。由练习 2.2.2, ˆ (q0,xk) =ˆ (ˆ (q0,xk-1),x) = ˆ (qf,x) [由归纳假设] = qf [由(a)]。 Exercise 2.2.10 Theautomatontellswhetherthenumberof1'sseeniseven(stateA)orodd(state B),acceptinginthelattercase.Itisaneasyinductionon|w|toshowthatdh(A,w) = A if and only if w has an even number of 1's. Basis: |w| = 0. Then w, the empty string surely has an even number of 1's, namely zero 1's, and ˆ (A,w) = A. Induction: Assume the statement for strings shorter than w. Then w = za, where a is either 0 or 1. Case1:a=0.Ifwhasanevennumberof1's,sodoesz.Bytheinductivehypothesis, ˆ (A,z)=A.ThetransitionsoftheDFAtellus ˆ (A,w)=A.Ifwhasanoddnumber of 1's, then so does z. By the inductive hypothesis, δ-hat(A,z) = B, and the transitions of the DFA tell usδ-hat(A,w) = B. Thus, in this case,δ-hat(A,w) = A if and only if w has an even number of 1's. Case2: a = 1. If w has an even number of 1's,then z has an odd number of 1's. By the inductive hypothesis, δ-hat(A,z) = B. The transitions of the DFA tell us δ-hat(A,w) = A. If w has an odd number of 1's, then z has an even number of 1's. By theinductive hypothesis,δ-hat(A,z) = A,and the transitionsof the DFA tell us δ-hat(A,w) = B. Thus, in this case as well, δ-hat(A,w) = A if and only if w has an even number of 1's. 这个自动机表示，状态 A 表示偶数个 1，状态 B 表示奇数个 1，不管串有偶数个还是奇数个 1，都会被接受。当且仅当串 w 中有偶数个 1 时，ˆ (A,w) = A.。用归纳法证明如下基础: |w| = 0。空串当然有偶数个 1 ，即 0 个 1，且ˆ (A,w) = A. 5

归纳：假设对于比 w 短的串命题成立。令 w = za, 其中 a 为 0 或 1。情形 1： a = 0. 如果 w 有偶数个 1, 则 z 有偶数个 1。由归纳假设，ˆ (A,z) = A。由转移表的 DFA 知ˆ (A,w) = A.如果 w 有奇数个 1, 则 z 有奇数个 1. 由归纳假设，ˆ (A,z) = B, 由转移表的 DFA 知ˆ (A,w) = B. 因此这种情况下ˆ (A,w) = A 当且仅当 w 有偶数个 1。情形 2： a = 1. 如果 w 有偶数个 1, 则 z 有奇数个 1。由归纳假设，ˆ (A,z) = B. 由转移表的 DFA 知ˆ (A,w) = A. 如果 w 有奇数个 1, 则 z 有偶数个 1。由归纳假设, ˆ (A,z) = A, 由转移表的 DFA 知ˆ (A,w) = B. 因此这种情况下ˆ (A,w) = A 当且仅当 w 有偶数个 1. 综合上述情形，命题得证。 Solutions for Section 2.3 Exercise 2.3.1 HerearethesetsofNFAstatesrepresentedbyeachoftheDFAstatesAthroughH: A={p};B={p,q};C={p,r};D={p,q,r};E={p,q,s};F={p,q,r,s};G={p,r,s}; H = {p,s}. 下表就是利用子集构造法将 NFA 转化成的 DFA。其中构造的子集有：A = {p}; B = {p,q}; C = {p,r}; D = {p,q,r}; E = {p,q,s}; F = {p,q,r,s}; G = {p,r,s}; H = {p,s}. 0 1 ->A B A B D C C E A D F C *E F G *F F G *G E H *H E H Exercise 2.3.4(a) Theideaistouseastateqi,fori=0,1,...,9torepresenttheideathatwehave seenaninputiandguessedthatthisistherepeateddigitattheend.Wealsohave state qs, the initial state, and qf, the final state. We stay in state qs all the 6

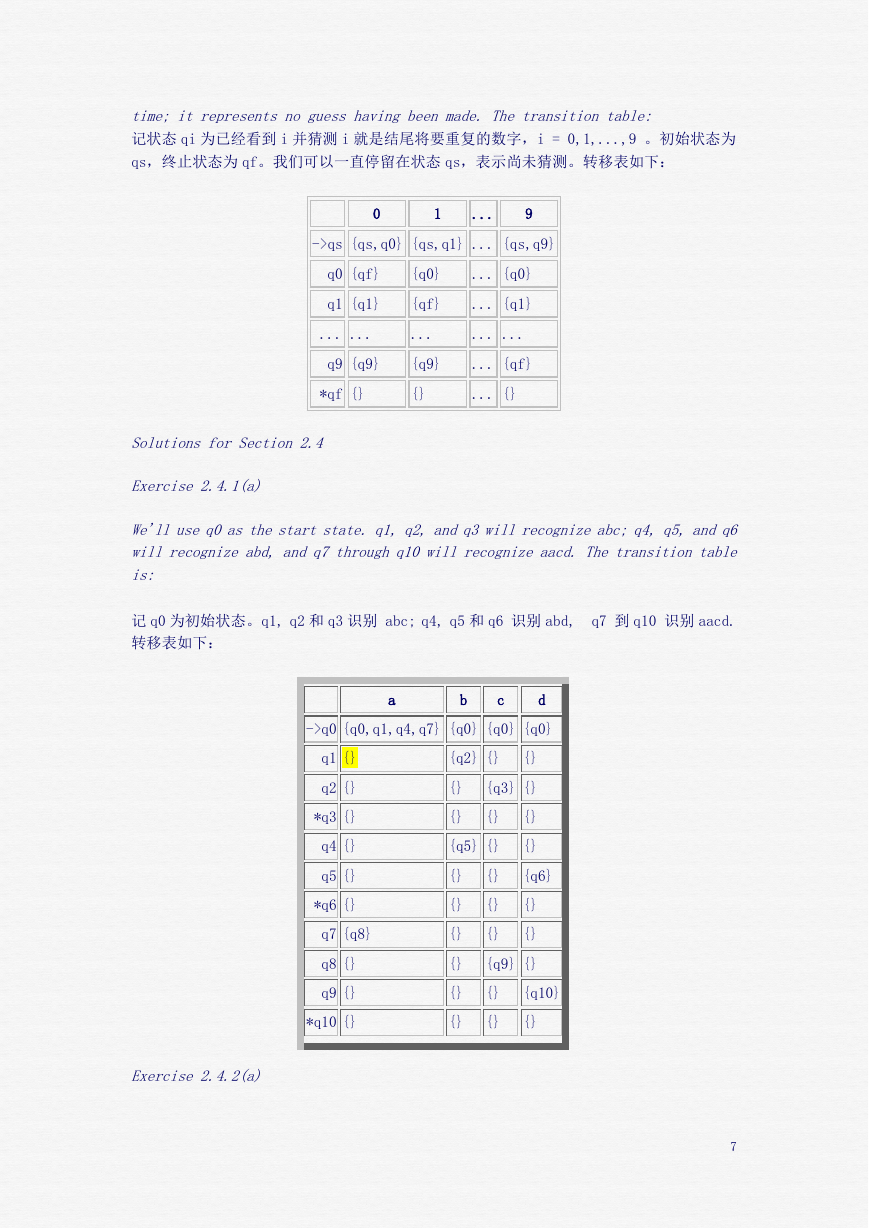
time; it represents no guess having been made. The transition table: 记状态 qi 为已经看到 i 并猜测 i 就是结尾将要重复的数字，i = 0,1,...,9 。初始状态为 qs，终止状态为 qf。我们可以一直停留在状态 qs，表示尚未猜测。转移表如下： 0 1 ... 9 ->qs {qs,q0} {qs,q1} ... {qs,q9} q0 {qf} q1 {q1} ... ... {q0} {qf} ... ... {q0} ... {q1} ... ... q9 {q9} {q9} ... {qf} *qf {} {} ... {} Solutions for Section 2.4 Exercise 2.4.1(a) We'lluseq0asthestartstate.q1,q2,andq3willrecognizeabc;q4,q5,andq6 will recognize abd, and q7 through q10 will recognize aacd. The transition table is: 记 q0 为初始状态。q1, q2 和 q3 识别 abc; q4, q5 和 q6 识别 abd, 转移表如下： q7 到 q10 识别 aacd. a b c d ->q0 {q0,q1,q4,q7} {q0} {q0} {q0} {q2} {} {} {q3} {} {q5} {} q1 {} q2 {} *q3 {} q4 {} q5 {} *q6 {} q7 {q8} q8 {} q9 {} *q10 {} Exercise 2.4.2(a) {} {} {} {} {} {} {q6} {} {} {} {} {} {} {} {} {} {} {q9} {} {} {} {q10} {} 7

Thesubsetconstructiongivesusthefollowingstates,eachrepresentingthesubset of the NFA states indicated: A = {q0}; B = {q0,q1,q4,q7}; C = {q0,q1,q4,q7,q8}; D = {q0,q2,q5}; E = {q0,q9}; F = {q0,q3}; G = {q0,q6}; H = {q0,q10}. Note that F, G andHcanbecombinedintooneacceptingstate,orwecanusethesethreestateto signal the recognition of abc, abd, and aacd, respectively. 由子集构造法可得以下 DFA 的状态，其中每一个状态都是 NFA 状态的子集： A = {q0}; B = {q0,q1,q4,q7}; C = {q0,q1,q4,q7,q8}; D = {q0,q2,q5}; E = {q0,q9}; F = {q0,q3}; G = {q0,q6}; H = {q0,q10}.注意到 F, G 和 H 可以整合到一个接受状态中，或者我们可以用这三个状态来分别标记已识别 abc, abd 和 aacd。 a b c d ->A B A A A B C D A A C C D E A D B A F G E B A A H *F B A A A *G B A A A *H B A A A Solutions for Section 2.5 Exercise 2.5.1 Forpart(a):theclosureofpisjust{p};forqitis{p,q},andforritis{p,q,r}. (a): 根据状态的ε闭包的的性质。求得， p 的ε闭包：{p}； q 的ε闭包：{p,q}； r 的ε闭包：{p,q,r}。 For (b), begin by noticing that a always leaves thestate unchanged. Thus, we can thinkoftheeffectofstringsofb'sandc'sonly.Tobegin,noticethattheonly waystogetfromptorforthefirsttime,usingonlyb,c,andε-transitionsare bb,bc,andc.Aftergettingtor, wecanreturntor readingeitherborc. Thus, everystringoflength3orless,consistingofb'sandc'sonly,isaccepted,with the exception of the string b. However, we have to allow a's as well. When we try to insert a's in these strings, yet keeping the length to 3 or less, we find that everystringofa'sb's,andc'swithatmostoneaisaccepted.Also,thestrings consisting of one c and up to 2 a's are accepted; other strings are rejected. b) 由于输入 a 状态总是保持不变，因此只需考虑输入 b 和 c 的情况。可以看出，从状态 p 第一次到 r 且只经过 b，c 和ε转移的路径为 bb, bεc 和 c ；到 r 之后，读入 b 仍可回到 r，读入 c 回到 p ，则可通过继续读入串 bb, bc 和 c 回到 r。 8

分享到：

赞收藏

资料库

Introduction to Automata Theory, Languages, and Computation(Seco....doc

相关推荐

课程资源

热门标签

最新资料