3-PRS 并联机器人工作空间分析 http://www.paper.edu.cn 李王英，徐尤南，刘志强 华东交通大学机电工程学院，南昌(330013) E-mail：ylshu115@sina.com 摘 要：本文分析了 3-PRS 并联机器人机构的位置逆解及工作空间的约束条件，采用极限 边界数值搜索法求解了 3-PRS 并联机器人工作空间,并利用 Matlab 对其工作空间进行三维仿 真分析。由于工作空间是随着机构结构参数的变化而变化，分析了其主要参数变化对机构工 作空间的影响。通过机构参数变化对工作空间的影响分析，为其最优工作空间设计奠定基础。 关键词：并联机器人；位置逆解；工作空间 中图分类号：TH12 1. 引言 并联机器人工作空间的求解方法主要有两种，一种是解析求解，一种是数值求解。解析 求解是一个非常复杂的问题，它在很大程度上依赖于机构位置正解的研究成果，至今仍没有 完善的方法，对于比较简单的平面并联机器人工作空间可以解析表达，而对于空间并联机器 人，目前还只有数值解法。数值法[1][2]的思路一般是根据平台的约束条件搜索工作空间边界， 主要有网格法、Jacobin 法、Monte Carlo 法和优化法，这些算法一般依赖于位置逆解，而且 必须固定末端执行器姿态。 本文对 3-PRS 并联机器人[3]的运动学位置逆解[4]进行详细分析，然后根据机器人结构特 点，分析了影响其工作空间的主要因素－驱动杆杆长的影响及运动副转角的影响，基于并联 机器人机构的位置逆解及工作空间的约束条件，确定采用极限边界数值搜索法来求解 3-PRS 并联机器人工作空间。最后利用 Matlab 对其工作空间进行三维仿真分析，并分析了其主要 结构参数变化对工作空间的影响。 2. 3-PRS 并联机器人模型及其位置逆解 图 1 3-PRS 并联机器人模型 - 1 - 

http://www.paper.edu.cn 3-PRS 三足并联机器人模型如图 1 所示，b1b2b3d1d2d3 为静平台（BP, Base Platform）， b1d1、b2d2、b3d3 为导杆(Guide way)，s1p1、s2p2、s3p3 为滑杆(Sliding-leg)，p1p2p3 为动平台（MP, Moving Platform，操作设备安装在它的中心位置）。p1、p2、p3 为球面副(S)，s1、s2、s3 处 分别有一小型构件，起连接滑杆和导杆的作用，此构件与导杆为移动副(P)连接，与滑杆为 旋转副(R)连接。三根导杆长度相同，与底面夹角相等，静平台的底面 b1b2b3、动平台 p1p2p3 和顶面 d1d2d3 都为等边三角形。 图 1 中，设静平台半径为 aR ，动平台半径为 bR ，导杆长度为 lg，第 i 个导杆与静平台 底面的夹角为 0iβ 。 根据图1定义的坐标系统，第i 个连接到动平台上的球关节的位置如下式： p h Rp ＝ ＋ (1) i ′ip 代表的是相同点 是第i 个球关节在定坐标系 O-xyz 中的位置, ′ i 是动平台的位置向量，即为动 其中 p i = [ p ix , p iy , ] T p iz − , x y z , c =h 中的位置， [ 在动平台上的动坐标系C x y z′ ′ ′ 平台中心点 C 在定坐标系中的位置向量， R 是动平台的旋转矩阵即： c s c + y s c s − y x c c θ θ y x c c θ θ θ θ θ θ θ θ θ θ θ θ z x s c θ θ θ θ θ θ θ θ θ θ θ θ z x s − θ y s − s + y x c s θ θ y x s c z c c z s s z c s z c s z s s r 13 r 23 r 33 r 11 r 21 r 31 r 12 r 22 r 32 ⎡ ⎢= ⎢ ⎢ ⎣ R ]T = c c y x x x x y y z z z ⎤ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ ⎢ ⎢ ⎣ (2) ⎤ ⎥ ⎥ ⎥ ⎦ 式中，‘s’、‘c’分别代表‘sin’和‘cos’。 由于滑杆受旋转关节限制，向量 ip 被约束在平面 i Ob s p 内，，则有约束方程： i i iα为第i 个导杆在 x-y 平面与 x 轴的夹角，由方程(1)、方程(2)、方程(3)可得： p iy pα= ) ix tan( i (3) y + r p r p ) ( ′ ′ + + α iy ix i 12 11 设三角形动平台的边长为lp ，再根据 iα分别为 1 90α = 150 ° ， 2 α = − 方程(4)中，经过数学演算，则得： r p ′ iy 22 r p ′ ix 21 tan x c = + c (4) ° ， 3 α = − ° ，代入 30 x c = − 3 3 lp c s z θ θ θ θ θ x s c z − s ( y x ) (5a) y c = 3 6 lp c c z θ θ θ θ θ θ θ x c c z + + s s s ( y y x z ) (5b) θ z = arctan ⎛ ⎜ ⎜ ⎝ s θ θ y c c θ θ y s x − x (5c) ⎞ ⎟ ⎟ ⎠ 则求位置逆解时，当已知独立变量θx 、θy 、 cz ，即可求得因变量 cx 、 cy 、θz ，从而 确定h 、 R 的值，则可求出 ip 。 3-PRS 型并联机器人位置逆解即为已知动平台位置，求输入量 p + l (6) 其中： ip 即可以根据逆解求解的已知条件求出即 s 可 p i 以在广义坐标系 O-xyz 表示出，另滑杆长度 il 均为已知，从而可以从下列运动学逆解方程中 (i = 1、2、3) h Rp p [ ix ，而 +i ＝ ＋ i ′ = i ] T i i i = b i + s iS 。由图 1 得出： b p , iy p iz , - 2 - 

求出输入杆长 iS ： http://www.paper.edu.cn p i − b ( i + s i ) = il (7) 3. 影响工作空间的主要因素 S i S S ≤ ≤ min 该并联机构是由连接固定平台的驱动杆来驱动的，对驱动杆的杆长限制分别用 minS 和 maxS 来表示驱动连杆在并联机器人工作中所能达到的极限位置，即要满足： (8) 机器人的上平台与各分支杆相连的关节都是球面副，球面副的转角θ是由与球面副的基 座固接的坐标系的 Z 轴和表示与球面副连接的杆向量 il 之间的夹角，球面副的转角都要受到 限制。若第i 个球面副的基座的 Z 向向量用 pin 表示，球面副所能达到的最大角度为 max pθ ， 则球面副的转角约束条件可以用下列式子表示： ⋅l R ( i l (9) arccos θ ＝ pi θ p n max max i ) pi ≤ 4. 工作空间的确定方法 本文基于并联机器人机构的位置逆解及工作空间的约束条件，采用极限边界数值搜索法 来求解并联机器人工作空间。此方法算法原理如下： 并联机器人工作空间可以看成是由无数个离散点所组成的，其中每个离散点都对应着动 平台的一个位姿。而前面己经得到了位置逆解模型，对于每个特定的动平台位姿，根据位置 逆解公式计算，先判断是否满足其约束条件，只要不满足其中的任何一个约束，那么这个给 定的位姿就不存在，也即与此位姿对应的离散点不在工作空间内。反之，在所给的位姿完全 满足约束条件时，若计算的结果等于任何一个约束边界值 minS 、 maxS 、或 max pθ ，则与位姿 对应的离散点就一定在工作空间的边界曲面上，由此，就能完全得到并联机器人工作空间的 边界曲面。 为了分析和评价机构工作空间的大小，这里我们利用角度体积来衡量工作工件，即： V 1 = ∫∫∫ 2 v z d d dz θρ ρ θ (10) 其中θ为极角， ρ为极径。 5. 工作空间仿真分析 l l 初始化机构结构参数如下： 1 200mm lg β β β ε = = 图中θx 用α表示、 yθ 用β表示。 ， 10 = = = = 20 30 l 3 = = 2 S 70 mm 350 0 = ， mm o ， min aR ， max = S mm bR 150 ， mm 200 = mm 80 = ， ， max 30 pθ o＝ 。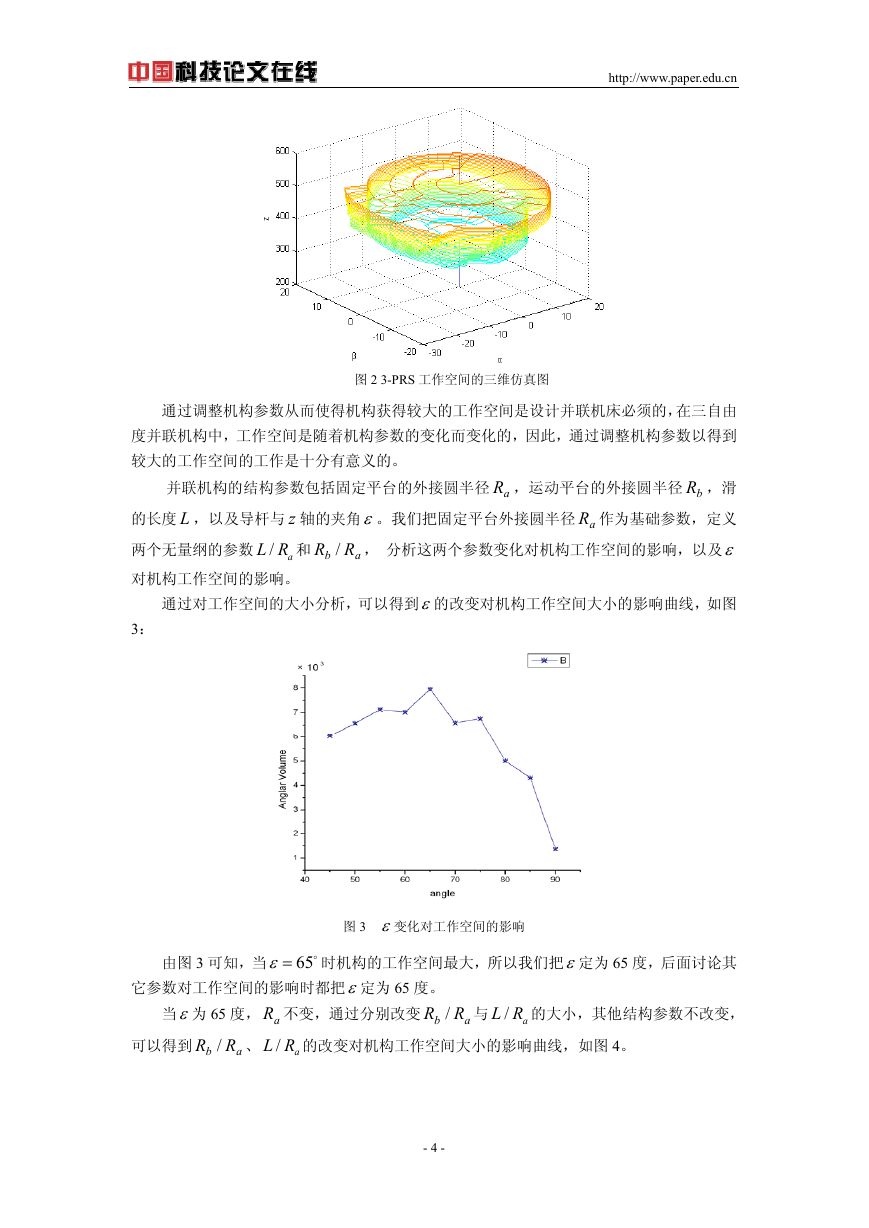 Matlab 是一种很好的用于数学计算的编程语言，它还提供了许多专用的工具箱，例如 Robot 工具箱，这里我们就借助 Matlab 编程进行工作空间的仿真，得到工作空间的三维仿真 图，如图 2 所示。 - 3 - 

http://www.paper.edu.cn 图 2 3-PRS 工作空间的三维仿真图 通过调整机构参数从而使得机构获得较大的工作空间是设计并联机床必须的，在三自由 度并联机构中，工作空间是随着机构参数的变化而变化的，因此，通过调整机构参数以得到 较大的工作空间的工作是十分有意义的。 并联机构的结构参数包括固定平台的外接圆半径 aR ，运动平台的外接圆半径 bR ，滑 的长度 L ，以及导杆与 z 轴的夹角ε。我们把固定平台外接圆半径 aR 作为基础参数，定义 L R 和 b RR / ， 分析这两个参数变化对机构工作空间的影响，以及ε 两个无量纲的参数 / 对机构工作空间的影响。 a a 通过对工作空间的大小分析，可以得到ε的改变对机构工作空间大小的影响曲线，如图 3： 图 3 ε变化对工作空间的影响 由图 3 可知，当 65ε= o 时机构的工作空间最大，所以我们把ε定为 65 度，后面讨论其 它参数对工作空间的影响时都把ε定为 65 度。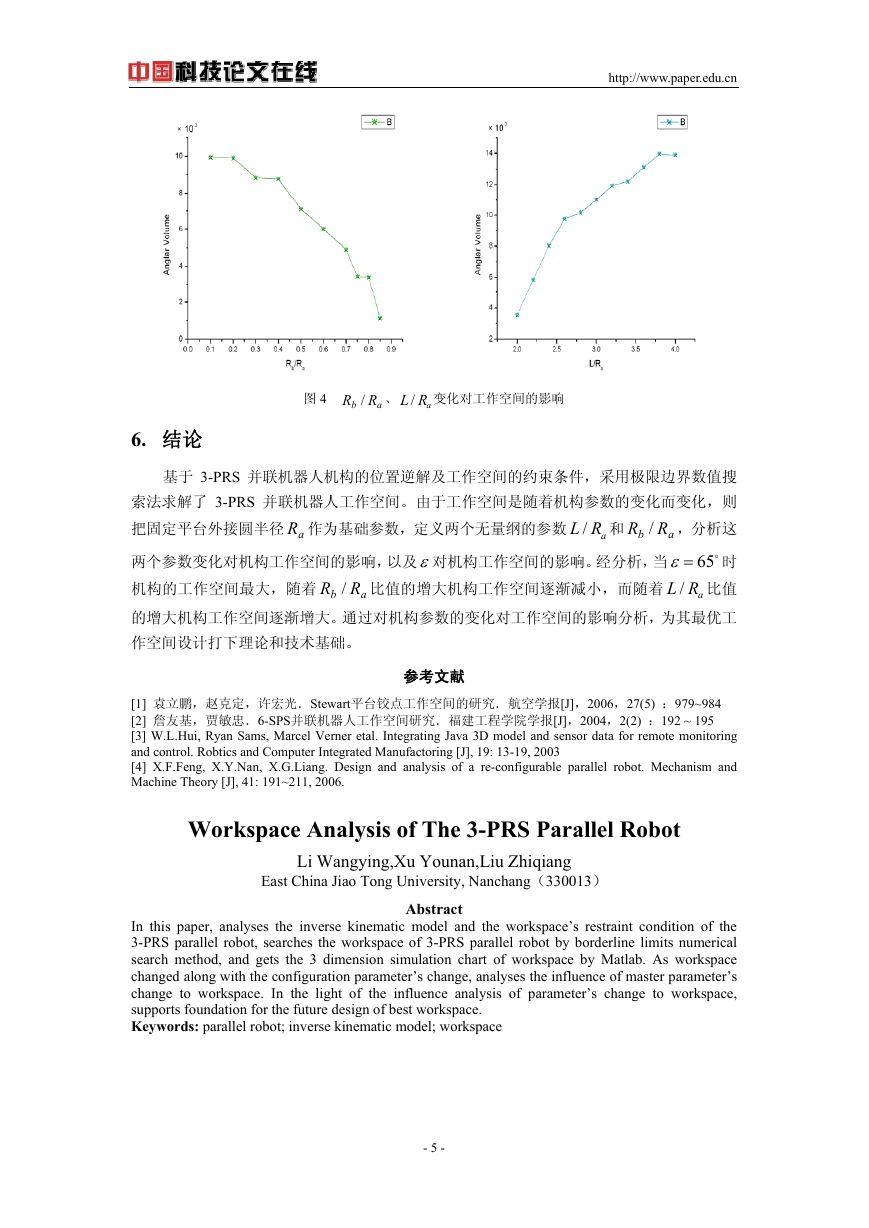 当ε为 65 度， aR 不变，通过分别改变 b RR / 与 / a L R 的大小，其他结构参数不改变， a 可以得到 b RR / 、 / a a L R 的改变对机构工作空间大小的影响曲线，如图 4。 - 4 - 

http://www.paper.edu.cn 图 4 6. 结论 b RR / 、 / a L R 变化对工作空间的影响 a 基于 3-PRS 并联机器人机构的位置逆解及工作空间的约束条件，采用极限边界数值搜 索法求解了 3-PRS 并联机器人工作空间。由于工作空间是随着机构参数的变化而变化，则 把固定平台外接圆半径 aR 作为基础参数，定义两个无量纲的参数 / b RR / ，分析这 两个参数变化对机构工作空间的影响，以及ε对机构工作空间的影响。经分析，当 65ε= o 时 L R 比值 机构的工作空间最大，随着 b RR / 比值的增大机构工作空间逐渐减小，而随着 / L R 和 a a a a 的增大机构工作空间逐渐增大。通过对机构参数的变化对工作空间的影响分析，为其最优工 作空间设计打下理论和技术基础。 参考文献 [1] 袁立鹏，赵克定，许宏光．Stewart平台铰点工作空间的研究．航空学报[J]，2006，27(5) ：979~984 [2] 詹友基，贾敏忠．6-SPS并联机器人工作空间研究．福建工程学院学报[J]，2004，2(2) ：192 ~ 195 [3] W.L.Hui, Ryan Sams, Marcel Verner etal. Integrating Java 3D model and sensor data for remote monitoring and control. Robtics and Computer Integrated Manufactoring [J], 19: 13-19, 2003 [4] X.F.Feng, X.Y.Nan, X.G.Liang. Design and analysis of a re-configurable parallel robot. Mechanism and Machine Theory [J], 41: 191~211, 2006. Workspace Analysis of The 3-PRS Parallel Robot Li Wangying,Xu Younan,Liu Zhiqiang East China Jiao Tong University, Nanchang（330013） Abstract In this paper, analyses the inverse kinematic model and the workspace’s restraint condition of the 3-PRS parallel robot, searches the workspace of 3-PRS parallel robot by borderline limits numerical search method, and gets the 3 dimension simulation chart of workspace by Matlab. As workspace changed along with the configuration parameter’s change, analyses the influence of master parameter’s change to workspace. In the light of the influence analysis of parameter’s change to workspace, supports foundation for the future design of best workspace. Keywords: parallel robot; inverse kinematic model; workspace - 5 -