第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
学习线性代数.pdf
标量,向量,矩阵,张量
矩阵转置
矩阵加法
矩阵乘法
单位矩阵
矩阵的逆
范数
特征值分解
奇异值分解
PCA (主成分分析)
线性代数
朱明超
deityrayleigh@gmail.com
1 标量, 向量, 矩阵, 张量
1. 标量 (Scalar): 表⽰⼀个单独的数，通常⽤斜体⼩写字母表⽰，如 s 2 R; n 2 N。
2. 向量 (Vector)：表⽰一列数，这些数有序排列的，可以通过下标获取对应值，通常⽤粗体⼩写字母表⽰：x 2 Rn ，它表⽰元素取实数，且有 n
个元素，第⼀个元素表⽰为：x1。将向量写成列向量的形式：
(1)
2666664
3777775
x =
x1
x2
xn
[
]
有时需要向量的⼦集，例如第 1; 3; 6 个元素，那么我们可以令集合 S = f1; 3; 6g ，然后⽤ xS 来表⽰这个⼦集。另外，我们⽤符号 - 表⽰集合的补
集：x1 表⽰除 x1 外 x 中的所有元素，xS 表⽰除 x1; x3; x6 外 x 中的所有元素。
3. 矩阵 (Matrix): 表⽰⼀个二维数组，每个元素的下标由两个数字确定，通常⽤⼤写粗体字母表⽰：A 2 Rmn ，它表⽰元素取实数的 m ⾏ n 列
矩阵，其元素可以表⽰为：A1;1; Am;n 。我们⽤ : 表⽰矩阵的⼀⾏或者⼀列：Ai;: 为第 i ⾏，A:;j 为第 j 列。
矩阵可以写成这样的形式：
有时我们需要对矩阵进⾏逐元素操作，如将函数 f 应⽤到 A 的所有元素上，此时我们⽤ f (A)i;j 表⽰。
4. 张量 (Tensor): 超过二维的数组，我们⽤ A 表⽰张量，Ai;j;k 表⽰其元素（三维张量情况下）。
A1;1 A1;2
A2;1 A2;2
(2)
[1]: import numpy as np
[2]: # 标量
s = 5
# 向量
v = np.array([1,2])
# 矩阵
m = np.array([[1,2], [3,4]])
# 张量
t = np.array([
[[1,2,3],[4,5,6],[7,8,9]],
[[11,12,13],[14,15,16],[17,18,19]],
[[21,22,23],[24,25,26],[27,28,29]],
])
print("标量: " + str(s))
print("向量: " + str(v))
print("矩阵: " + str(m))
print("张量: " + str(t))
标量: 5
向量: [1 2]
矩阵: [[1 2]
[3 4]]
张量: [[[ 1 2 3]
5 6]
[ 4
[ 7
8 9]]
[[11 12 13]
[14 15 16]
[17 18 19]]
[[21 22 23]
1
深度学习：线性代数
[24 25 26]
[27 28 29]]]
2 矩阵转置
矩阵转置 (Transpose) 相当于沿着对角线翻转，定义如下：
矩阵转置的转置等于矩阵本⾝：
转置将矩阵的形状从 m n 变成了 n m 。
⊤
i;j = Ai;j
A
⊤
A
= A
(
)⊤
向量可以看成是只有一列的矩阵，为了⽅便，我们可以使⽤⾏向量加转置的操作，如：x = [x1; x2; x3]
⊤。
标量也可以看成是一行一列的矩阵，其转置等于它⾃⾝：a
⊤
= a 。
[3]: A = np.array([[1.0,2.0],[1.0,0.0],[2.0,3.0]])
A_t = A.transpose()
print("A:", A)
print("A 的转置:", A_t)
A: [[1. 2.]
[1. 0.]
[2. 3.]]
A 的转置: [[1. 1. 2.]
[2. 0. 3.]]
3 矩阵加法
加法即对应元素相加，要求两个矩阵的形状⼀样：
数乘即一个标量与矩阵每个元素相乘：
C = A + B; Ci;j = Ai;j + Bi;j
D = a B + c; Di;j = a Bi;j + c
朱明超
(3)
(4)
(5)
(6)
有时我们允许矩阵和向量相加的，得到⼀个矩阵，把 b 加到了 A 的每⼀⾏上，本质上是构造了⼀个将 b 按⾏复制的⼀个新矩阵，这种机制叫做⼴
播 (Broadcasting)：
C = A + b; Ci;j = Ai;j + bj
[4]: a = np.array([[1.0,2.0],[3.0,4.0]])
b = np.array([[6.0,7.0],[8.0,9.0]])
print("矩阵相加：", a + b)
矩阵相加： [[ 7. 9.]
[11. 13.]]
4 矩阵乘法
两个矩阵相乘得到第三个矩阵，我们需要 A 的形状为 m n，B 的形状为 n p，得到的矩阵为 C 的形状为 m p：
具体定义为
C = AB
∑
Ci;j =
Ai;kBk;j
k
注意矩阵乘法不是元素对应相乘，元素对应相乘又叫 Hadamard 乘积，记作 A ⊙ B。
⊤
向量可以看作是列为 1 的矩阵，两个相同维数的向量 x 和 y 的点乘（Dot Product）或者内积，可以表⽰为 x
y。
我们也可以把矩阵乘法理解为：Ci;j 表⽰ A 的第 i ⾏与 B 的第 j 列的点积。
2
(7)
(8)
(9)
深度学习：线性代数
朱明超
[5]: m1 = np.array([[1.0,3.0],[1.0,0.0]])
m2 = np.array([[1.0,2.0],[5.0,0.0]])
print("按矩阵乘法规则：", np.dot(m1, m2))
print("按逐元素相乘：", np.multiply(m1, m2))
print("按逐元素相乘：", m1*m2)
v1 = np.array([1.0,2.0])
v2 = np.array([4.0,5.0])
print("向量内积：", np.dot(v1, v2))
2.]]
按矩阵乘法规则： [[16. 2.]
[ 1.
按逐元素相乘： [[1. 6.]
[5. 0.]]
按逐元素相乘： [[1. 6.]
[5. 0.]]
向量内积： 14.0
5 单位矩阵
为了引⼊矩阵的逆，我们需要先定义单位矩阵 (Identity Matrix)：单位矩阵乘以任意⼀个向量等于这个向量本⾝。记 In 为保持 n 维向量不变的
单位矩阵，即：
In 2 Rnn; 8x 2 Rn; Inx = x
26641 0 0
0 1 0
3775
0 0 1
单位矩阵的结构⼗分简单，所有的对⾓元素都为 1 ，其他元素都为 0 ，如：
I3 =
[6]: np.identity(3)
[6]: array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
6 矩阵的逆
矩阵 A 的逆 (Inversion) 记作 A
1 ，定义为⼀个矩阵使得
1A = In
A
如果 A
1 存在，那么线性⽅程组 Ax = b 的解为：
1Ax = Inx = x = A
1b
A
[7]: A = [[1.0,2.0],[3.0,4.0]]
A_inv = np.linalg.inv(A)
print("A 的逆矩阵", A_inv)
A 的逆矩阵 [[-2.
[ 1.5 -0.5]]
1. ]
7 范数
通常我们⽤范数 (norm) 来衡量向量，向量的 Lp 范数定义为：
∥x∥p =
) 1
p
jxijp
(∑
i
; p 2 R; p 1
(10)
(11)
(12)
(13)
(14)
L2 范数，也称欧⼏⾥得范数 (Euclidean norm)，是向量 x 到原点的欧几里得距离。有时也⽤ L2 范数的平⽅来衡量向量：x
范数在计算上更为便利，例如它的对 x 梯度的各个分量只依赖于 x 的对应的各个分量，⽽ L2 范数对 x 梯度的各个分量要依赖于整个 x 向量。
x 。事实上，平⽅ L2
⊤
3
深度学习：线性代数
朱明超
L1 范数：L2 范数并不⼀定适⽤于所有的情况，它在原点附近的增长就⼗分缓慢，因此不适⽤于需要区别 0 和⾮常⼩但是⾮ 0 值的情况。L1 范数
就是⼀个⽐较好的选择，它在所有⽅向上的增长速率都是⼀样的，定义为：
它经常使⽤在需要区分 0 和非 0 元素的情形中。
i
L0 范数：如果需要衡量向量中⾮ 0 元素的个数，但它并不是一个范数 (不满⾜三⾓不等式和数乘)，此时 L1 范数可以作为它的⼀个替代。
1 范数：它在数学上是向量元素绝对值的最⼤值，因此也被叫做 (Max norm)：
L
jxij
∥x∥1 = max
i
有时我们想衡量⼀个矩阵，机器学习中通常使⽤的是 F 范数 (Frobenius norm)，其定义为：
(15)
(16)
(17)
∑
∥x∥1 =
jxij
√∑
A2
i;j
i;j
∥A∥F =
[8]: a = np.array([1.0,3.0])
print("向量 2 范数", np.linalg.norm(a,ord=2))
print("向量 1 范数", np.linalg.norm(a,ord=1))
print("向量无穷范数", np.linalg.norm(a,ord=np.inf))
向量 2 范数 3.1622776601683795
向量 1 范数 4.0
向量无穷范数 3.0
[9]: a = np.array([[1.0,3.0],[2.0,1.0]])
print("矩阵 F 范数", np.linalg.norm(a,ord="fro"))
矩阵 F 范数 3.872983346207417
8 特征值分解
如果⼀个 n n 矩阵 A 有 n 组线性⽆关的单位特征向量 fv(1); : : : ; v(n)g ，以及对应的特征值 1; : : : ; n 。将这些特征向量按列拼接成⼀个矩阵：
V = [v(1); : : : ; v(n)] ，并将对应的特征值拼接成⼀个向量： = [1; : : : ; n] 。
A 的特征值分解 (Eigendecomposition) 为：
1
(18)
A = V diag()V
注意：
• 不是所有的矩阵都有特征值分解
• 在某些情况下，实矩阵的特征值分解可能会得到复矩阵
[10]: A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0],
[7.0,8.0,9.0]])
# 计算特征值
print("特征值:", np.linalg.eigvals(A))
# 计算特征值和特征向量
eigvals,eigvectors = np.linalg.eig(A)
print("特征值:", eigvals)
print("特征向量:", eigvectors)
特征值: [ 1.61168440e+01 -1.11684397e+00 -3.73313677e-16]
特征值: [ 1.61168440e+01 -1.11684397e+00 -3.73313677e-16]
特征向量: [[-0.23197069 -0.78583024 0.40824829]
[-0.52532209 -0.08675134 -0.81649658]
[-0.8186735
0.61232756 0.40824829]]
4
深度学习：线性代数
9 奇异值分解
朱明超
奇异值分解 (Singular Value Decomposition, SVD) 提供了另⼀种分解矩阵的⽅式，将其分解为奇异向量和奇异值。
与特征值分解相⽐，奇异值分解更加通⽤，所有的实矩阵都可以进⾏奇异值分解，⽽特征值分解只对某些⽅阵可以。
奇异值分解的形式为：
(19)
若 A 是 m n 的，那么 U 是 m m 的，其列向量称为左奇异向量，⽽ V 是 n n 的，其列向量称为右奇异向量，⽽ 是 m n 的⼀个对⾓矩
阵，其对⾓元素称为矩阵 A 的奇异值。
A = U V
⊤
事实上，左奇异向量是 AA
⊤
⊤ 的特征向量，⽽右奇异向量是 A
A 的特征向量，⾮ 0 奇异值的平⽅是 A
⊤
A 的⾮ 0 特征值。
[11]: A = np.array([[1.0,2.0,3.0],
[4.0,5.0,6.0]])
U,D,V = np.linalg.svd(A)
print("U:", U)
print("D:", D)
print("V:", V)
U: [[-0.3863177 -0.92236578]
[-0.92236578 0.3863177 ]]
D: [9.508032
0.77286964]
V: [[-0.42866713 -0.56630692 -0.7039467 ]
[ 0.80596391 0.11238241 -0.58119908]
[ 0.40824829 -0.81649658 0.40824829]]
10 PCA (主成分分析)
假设我们有 m 个数据点 x(1); : : : ; x(m) 2 Rn ，对于每个数据点 x(i) ，我们希望找到⼀个对应的点 c(i) 2 Rl; l < n 去表⽰它 (相当于对它进⾏降维)，
并且让损失的信息量尽可能少。
我们可以将这个过程看作是⼀个编码解码的过程，设编码和解码函数分别为 f; g ，则有 f (x) = c; x g(f (x))。考虑⼀个线性解码函数 g(c) =
Dc; D 2 Rnl ，为了计算⽅便，我们将这个矩阵的列向量约束为相互正交的。另⼀⽅⾯，考虑到存在尺度放缩的问题，我们将这个矩阵的列向量约
束为具有单位范数来获得唯⼀解。
对于给定的 x ，我们需要找到信息损失最⼩的 c⋆ ，即求解：
c⋆ = arg min
c
∥x g(c)∥2 = arg min
c
∥x g(c)∥2
2
这⾥我们⽤⼆范数来衡量信息的损失。展开之后我们有：
∥x g(c)∥2
2 = (x g(c))
⊤
(x g(c)) = x
⊤
x 2x
⊤
⊤
g(c) + g(c)
g(c)
结合 g(c) 的表达式，忽略不依赖 c 的 x
⊤
x 项，我们有：
c⋆ = arg min
c
= arg min
c
= arg min
c
2x
⊤
2x
⊤
2x
⊤
Dc + c
⊤
⊤
D
Dc
Dc + c
Dc + c
⊤
⊤
Ilc
c
这⾥ D 具有单位正交性。
对 c 求梯度，并令其为零，我们有：
因此，我们的编码函数为：
此时通过编码解码得到的重构为：
Dc + c
⊤
c) = 0
▽▽▽c(2x
⊤
2D
⊤
x + 2c = 0
c = D
⊤
x
f (x) = D
⊤
x
r(x) = g(f (x)) = DD
⊤
x
5
(20)
(21)
(22)
(23)
(24)
(25)
深度学习：线性代数
朱明超
接下来求解最优的变换 D 。由于我们需要将 D 应⽤到所有的 xi 上，所以我们需要最优化：
r(x(i))j)2
(x(i)
j
D⋆ = arg min
D
√∑
i;j
为了⽅便，我们考虑 l = 1 的情况，此时问题简化为：
考虑 F 范数，并进⼀步的推导：
⊤
s:t: D
D = Il
∑
i
d⋆ = arg min
d
⊤
s:t: d
d = 1
d⋆ = arg max
d
⊤
s:t: d
d = 1
dd
⊤
(i)
x
))2
(x(i)
j
Tr(d
⊤
⊤
X
Xd)
(26)
(27)
(28)
优化问题可以⽤特征分解来求解。但实际计算时，我们会采⽤如下⽅式计算：
PCA 将输⼊ x 投影表⽰成 c。c 是⽐原始输⼊维数更低的表⽰，同时使得元素之间线性⽆关。假设有⼀个 m n 的矩阵 X，数据的均值为零，即
E[x] = 0 ，X 对应的⽆偏样本协⽅差矩阵：Var [x] = 1
⊤
PCA 是通过线性变换找到一个 Var [c] 是对角矩阵的表⽰ c = V
的右奇异向量。假设 V 是 X = U V
⊤ 奇异值分解的右奇异向量，我们得到原来的特征向量⽅程：
x ，矩阵 X 的主成分可以通过奇异值分解 (SVD) 得到，也就是说主成分是 X
m1 X
X。
⊤
⊤
X
X = (U V
⊤
⊤
)
U V
⊤
⊤
= V
U
⊤
U V
⊤
= V 2V
⊤
(29)
m1 X
⊤
V 2V
⊤
X = 1
m1 V 2V
⊤ 。
V = 1
m1 2 ，因为根据奇异值定义 V
⊤
V = I 。c 的协⽅差是
因为根据奇异值的定义 U
⊤
U = I 。因此 X 的⽅差可以表⽰为：Var [x] = 1
所以 c 的协⽅差满⾜：Var [c] = 1
对⾓的，c 中的元素是彼此⽆关的。
m1 C
以 iris 数据为例，展⽰ PCA 的使⽤。
⊤
C = 1
m1 V
⊤
X
⊤
XV = 1
m1 V
⊤
[12]: import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
%matplotlib inline
[13]: # 载入数据
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()
[13]: 2
1
0
Name: label, dtype: int64
50
50
50
[14]: # 查看数据
df.tail()
[14]:
145
146
147
148
149
sepal length sepal width petal length petal width
2.3
1.9
2.0
2.3
1.8
5.2
5.0
5.2
5.4
5.1
6.7
6.3
6.5
6.2
5.9
3.0
2.5
3.0
3.4
3.0
label
2
2
2
2
2
[15]: # 查看数据
X = df.iloc[:, 0:4]
y = df.iloc[:, 4]
print("查看第一个数据： \n", X.iloc[0, 0:4])
print("查看第一个标签: \n", y.iloc[0])
6
朱明超
深度学习：线性代数
5.1
3.5
1.4
0.2
查看第一个数据：
sepal length
sepal width
petal length
petal width
Name: 0, dtype: float64
查看第一个标签:
0
[16]: class PCA():
def __init__(self):
pass
def fit(self, X, n_components):
n_samples = np.shape(X)[0]
covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(X - X.mean(axis=0))
# 对协方差矩阵进行特征值分解
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
# 对特征值（特征向量）从大到小排序
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx][:n_components]
eigenvectors = np.atleast_1d(eigenvectors[:, idx])[:, :n_components]
# 得到低维表示
X_transformed = X.dot(eigenvectors)
return X_transformed
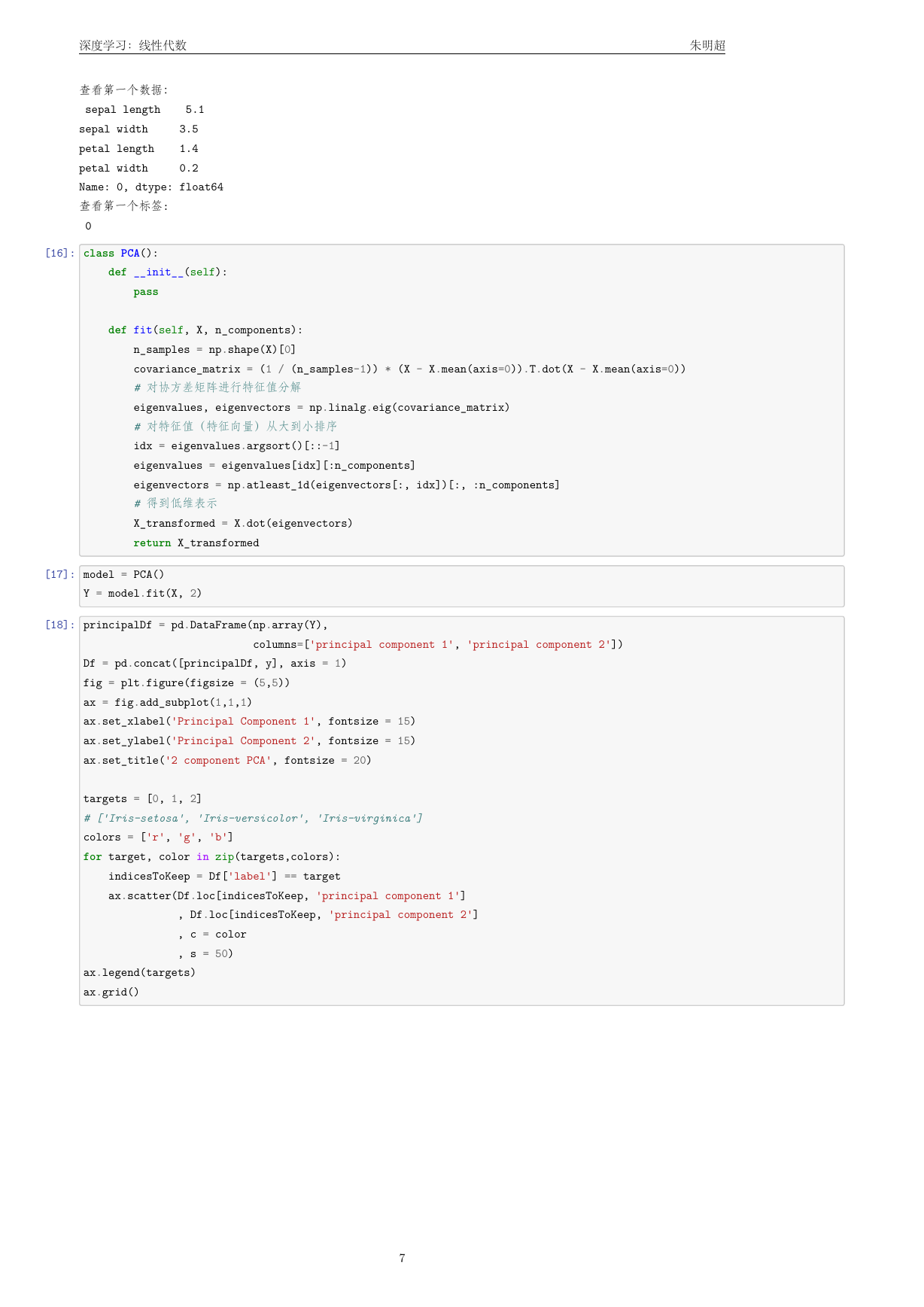
[17]: model = PCA()
Y = model.fit(X, 2)
[18]: principalDf = pd.DataFrame(np.array(Y),
columns=['principal component 1', 'principal component 2'])
Df = pd.concat([principalDf, y], axis = 1)
fig = plt.figure(figsize = (5,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = [0, 1, 2]
# ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = Df['label'] == target
ax.scatter(Df.loc[indicesToKeep, 'principal component 1']
, Df.loc[indicesToKeep, 'principal component 2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
7
深度学习：线性代数
朱明超
使⽤ sklearn 包实现 PCA
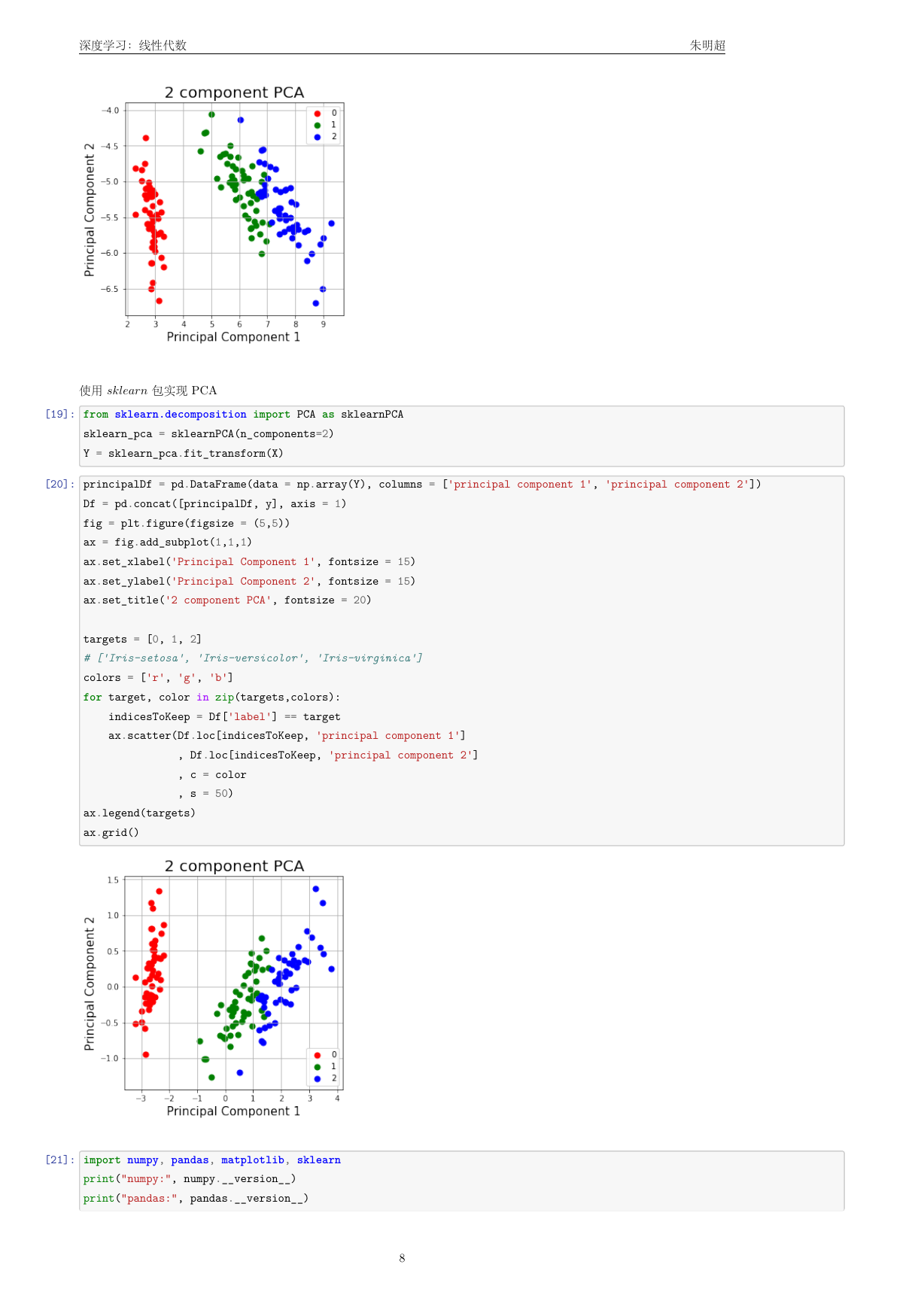
[19]: from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2)
Y = sklearn_pca.fit_transform(X)
[20]: principalDf = pd.DataFrame(data = np.array(Y), columns = ['principal component 1', 'principal component 2'])
Df = pd.concat([principalDf, y], axis = 1)
fig = plt.figure(figsize = (5,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = [0, 1, 2]
# ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = Df['label'] == target
ax.scatter(Df.loc[indicesToKeep, 'principal component 1']
, Df.loc[indicesToKeep, 'principal component 2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
[21]: import numpy, pandas, matplotlib, sklearn
print("numpy:", numpy.__version__)
print("pandas:", pandas.__version__)
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
