电荷泵锁相环mathcad设计文档.pdf-资料库

zb5700-5049320-16359647379561930795.pdf-第1页.png

第1页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第2页.png

第2页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第3页.png

第3页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第4页.png

第4页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第5页.png

第5页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第6页.png

第6页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第7页.png

第7页 / 共13页

zb5700-5049320-16359647379561930795.pdf-第8页.png

第8页 / 共13页

3rd Order PLL Design fR Kf Kv fO C2 R1 C1 1 N Fig. 1: 3rd-Order PLL with Current-Mode Phase-Detector useful functions and identities Units Constants _______________________________________ Table of Contents I. Introduction II. Inputs III. Design Procedure IV. Optimal Phase Margin for Minimum Settling V. Synthesis of Loop Filter Components VI. Integrated Loop Filter VII. Modified Loop Filter PLL Design Function VIII. IX. Copyright and Trademark Notice 2 S

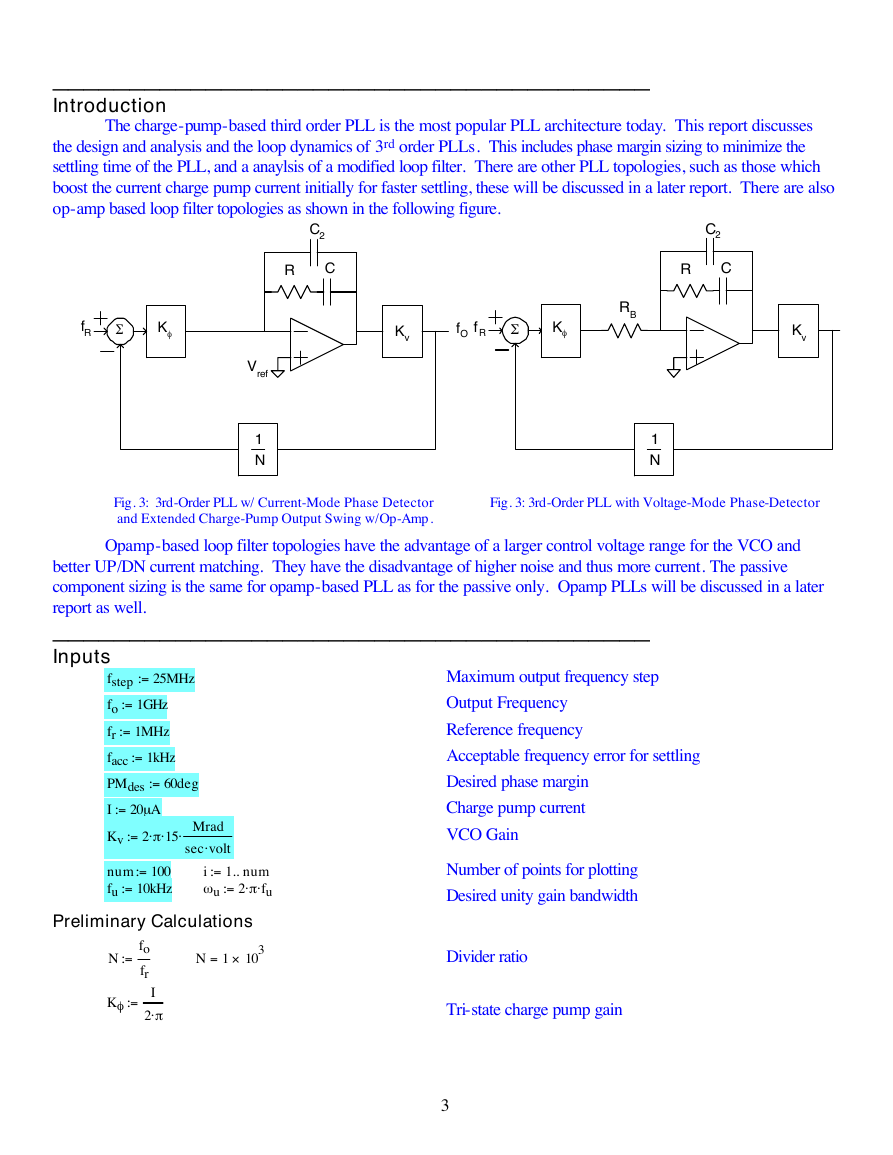
_______________________________________ Introduction The charge-pump-based third order PLL is the most popular PLL architecture today. This report discusses the design and analysis and the loop dynamics of 3rd order PLLs. This includes phase margin sizing to minimize the settling time of the PLL, and a anaylsis of a modified loop filter. There are other PLL topologies, such as those which boost the current charge pump current initially for faster settling, these will be discussed in a later report. There are also op-amp based loop filter topologies as shown in the following figure. C2 R C C2 R C fR Kf Kv fO f R Kf RB Kv Vref 1 N 1 N Fig. 3: 3rd-Order PLL w/ Current-Mode Phase Detector and Extended Charge-Pump Output Swing w/Op-Amp. Opamp-based loop filter topologies have the advantage of a larger control voltage range for the VCO and Fig. 3: 3rd-Order PLL with Voltage-Mode Phase-Detector better UP/DN current matching. They have the disadvantage of higher noise and thus more current. The passive component sizing is the same for opamp-based PLL as for the passive only. Opamp PLLs will be discussed in a later report as well. _______________________________________ Inputs := 25MHz 1GHz fstep := fo := fr facc PMdes := I Kv 1MHz := 1kHz := 20m A 2 p := 15 60deg Mrad sec volt Maximum output frequency step Output Frequency Reference frequency Acceptable frequency error for settling Desired phase margin Charge pump current VCO Gain := num 100 10kHz fu := := i w u 1 num.. fu := 2 p Preliminary Calculations 103 ·= N 1 := N fo fr := Kf I 2 p Number of points for plotting Desired unity gain bandwidth Divider ratio Tri-state charge pump gain 3 S S

_______________________________________ 3rd Order PLL Design Procedure Without a loop filter PLLs are a type I system a single pole at DC from the VCO voltage to phase transfer function. The loop filter accumulates the average charge from the charge pump to generate a fixed voltage to set the frequency of the VCO. This accumulation gives the loop another pole at DC. Thus the loop starts with a phase of -180 degrees. In order to insure stability and provide a smooth settling response the phase must be raised with a zero in the loop to provide a desired phase margin at the unity gain frequency of the open loop transfer function. This zero is introduced by adding a resistor in series with the main loop filter capacitor. To size the loop filter to provide a desired phase margin we first start by finding the open-loop unity-gain bandwidth. This requires the open-loop transfer function of the loop as shown in the following equation. GH s( ) Kf = ( 1 C1 C2+ ) s R1 C1 1+ s C1 C2 C1 C2+ + 1 R1 Kv s 1 N = Kf Kv ) ( N C1 C2+ s2 s s w z + 1 1+ s w p One design methodology is to place the zero below the unity gain bandwidth to increase the phase margin. The pole is placed an equal factor above the unity gain bandwidth. Let's call this factor wu_wz, then the transfer function becomes: w p w u wz_wu wu_wz GH s( ) 1+ w z = = = w u wz_wu s w u s Kf Kv ) ( N C1 C2+ s2 + 1 w u wu_wz u is given by the following equation The magnitude of this transfer function at w MagGH w u( ) wu_wz = Kf Kv ) ( N C1 C2+ 2 w u Now by setting the loop gain equal to unity, the unity gain bandwidth can be solved for with the result given in the following equation: Kv wu_wz Kf ) ( N C1 C2+ = w u 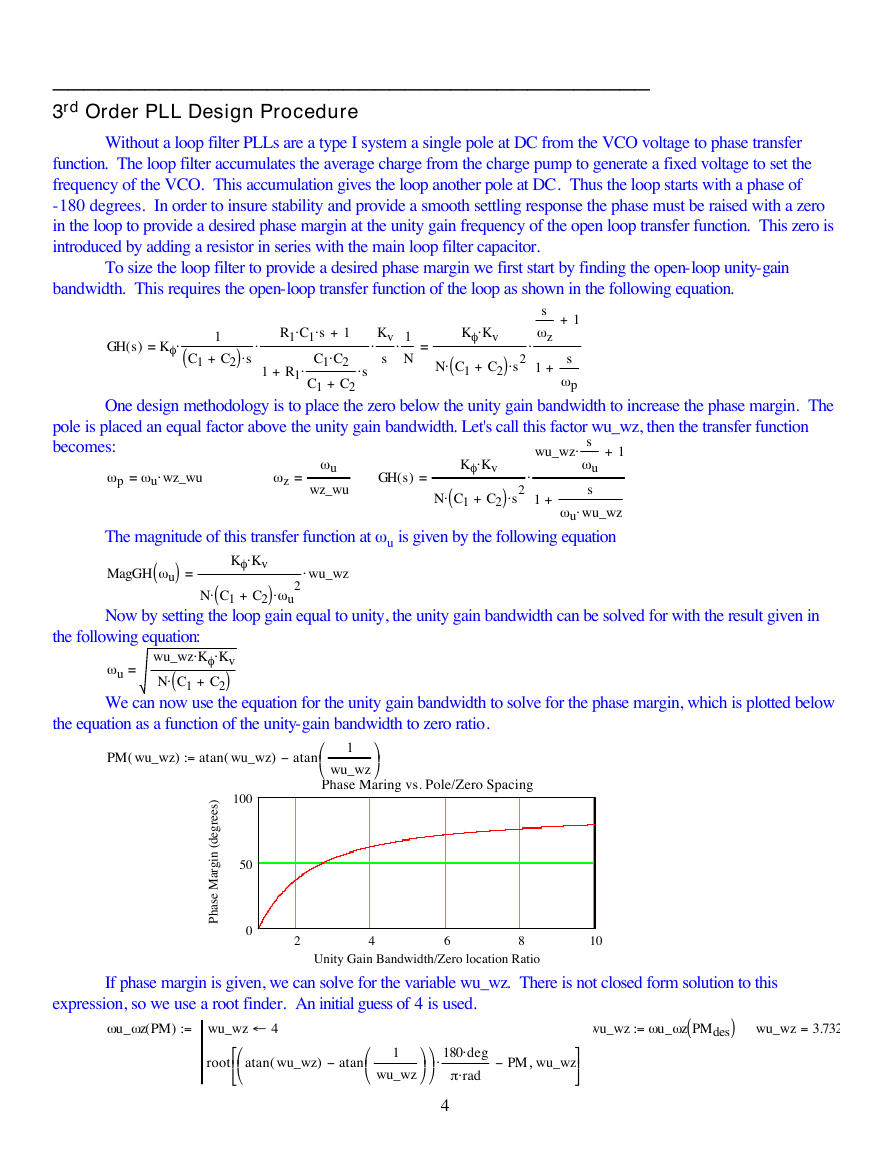We can now use the equation for the unity gain bandwidth to solve for the phase margin, which is plotted below the equation as a function of the unity-gain bandwidth to zero ratio. PM wu_wz ) ( := atan wu_wz ) ( atan 1 wu_wz Phase Maring vs. Pole/Zero Spacing ) s e e r g e d ( n i g r a M e s a h P 100 50 0 2 4 6 8 10 Unity Gain Bandwidth/Zero location Ratio If phase margin is given, we can solve for the variable wu_wz. There is not closed form solution to this expression, so we use a root finder. An initial guess of 4 is used. wu_wz := ( w u_w z PMdes ) wu_wz = 3.732 w u_w z PM( ) := wu_wz 4 root atan wu_wz ) ( atan 1 wu_wz 180 deg rad PM- , wu_wz 4 ‹ Ł ł - Ł ł p Ø Œ º ø œ ß Ł ł -

_______________________________________ Optimal Phase Margin for Minimum Settling Part of the design process involves entering a desired value of phase margin. The phase margin can effect the performance of several parameters including phase noise, loop bandwidth, and settling time. It's effect on some parameters is minor for typical values. Phase margin has it's biggest impact on settling time. Thus, settling time is used to optimized phase margin. The variable w u_w z is easier to work with than phase margin, so it will be used. There is a direct relationship between the two, which will be used to find the optimum phase margin. ClosedLoop s( ) = wu_wz The transient response of this system is: wu_wz 1+ N s w u 2 + s w u s w u 3 + wu_wz 1+ s w u ( ) h w ut wu_wz , := fstep 1 + 2 e wu_wz 1- 2 w ut cosh 1 2 wu_wz 1+ wu_wz 3- w ut w ut e ( wu_wz 1- ) wu_wz 3- For the case where wu_wz=3 the response is ( ) h w ut wu_wz We can write a single expression for the transient response in both cases, when wu_wz is and isn't 3. 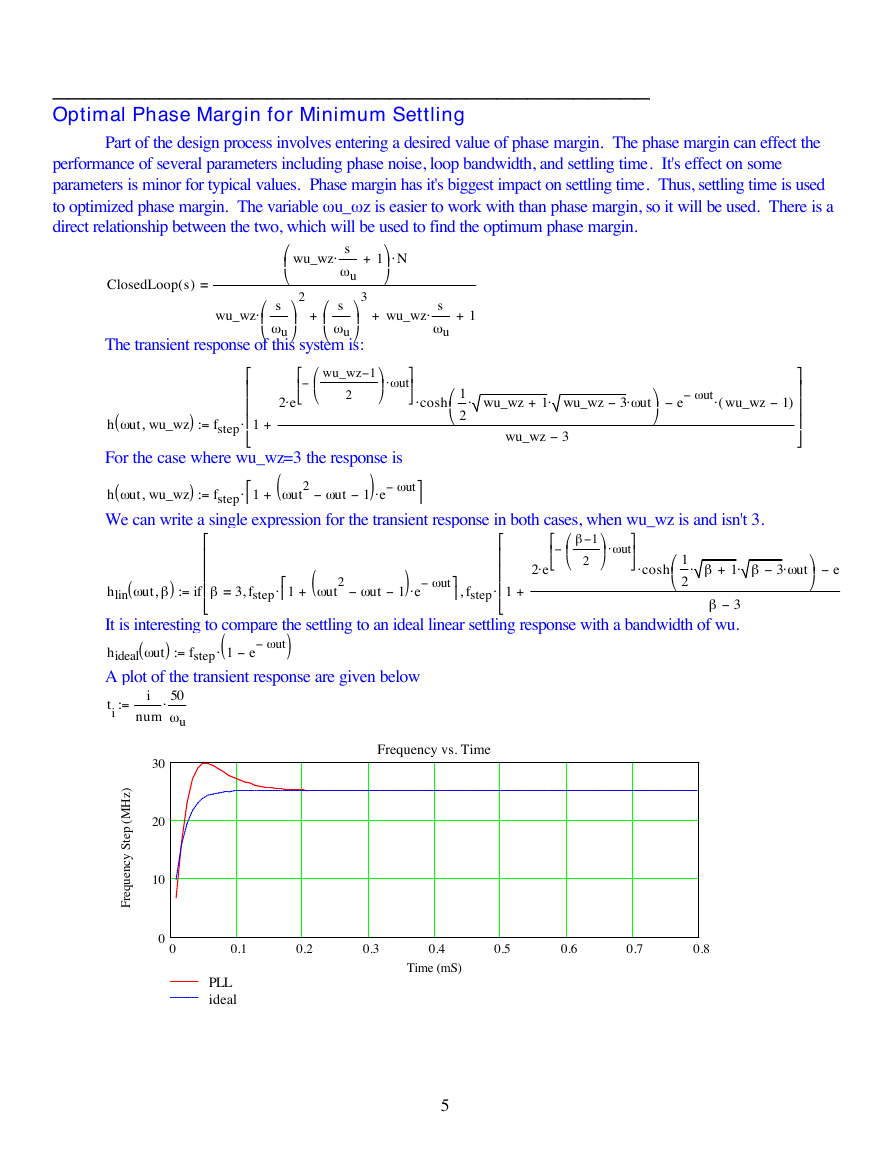fstep 1 ) e w ut w ut 1- w ut := ( + 2 , 1- 2 w ut cosh 1 2 2 e 1+ 3- w ut e- ( 2 ) e w ut , ( ) , e + := 3= if b 1- w ut w ut fstep 1 ) hlin w ut b, 3- It is interesting to compare the settling to an ideal linear settling response with a bandwidth of wu. hideal w ut A plot of the transient response are given below ti ( fstep 1 fstep 1 w ut := := + ( ) i num 50 w u ) z H M ( p e t S y c n e u q e r F 30 20 10 0 0 Frequency vs. Time 0.1 0.2 0.3 PLL ideal 0.4 Time (mS) 0.5 0.6 0.7 0.8 5 Ł ł Ł ł Ł ł Ł ł - Ø Œ º ø œ ß Ł ł - - Ø Œ Œ Œ º ø œ œ œ ß - - Ø º ø ß - - Ø º ø ß b Ł ł - Ø Œ º ø œ ß b b Ł ł b Ø Œ Œ Œ º Ø Œ Œ Œ º - -

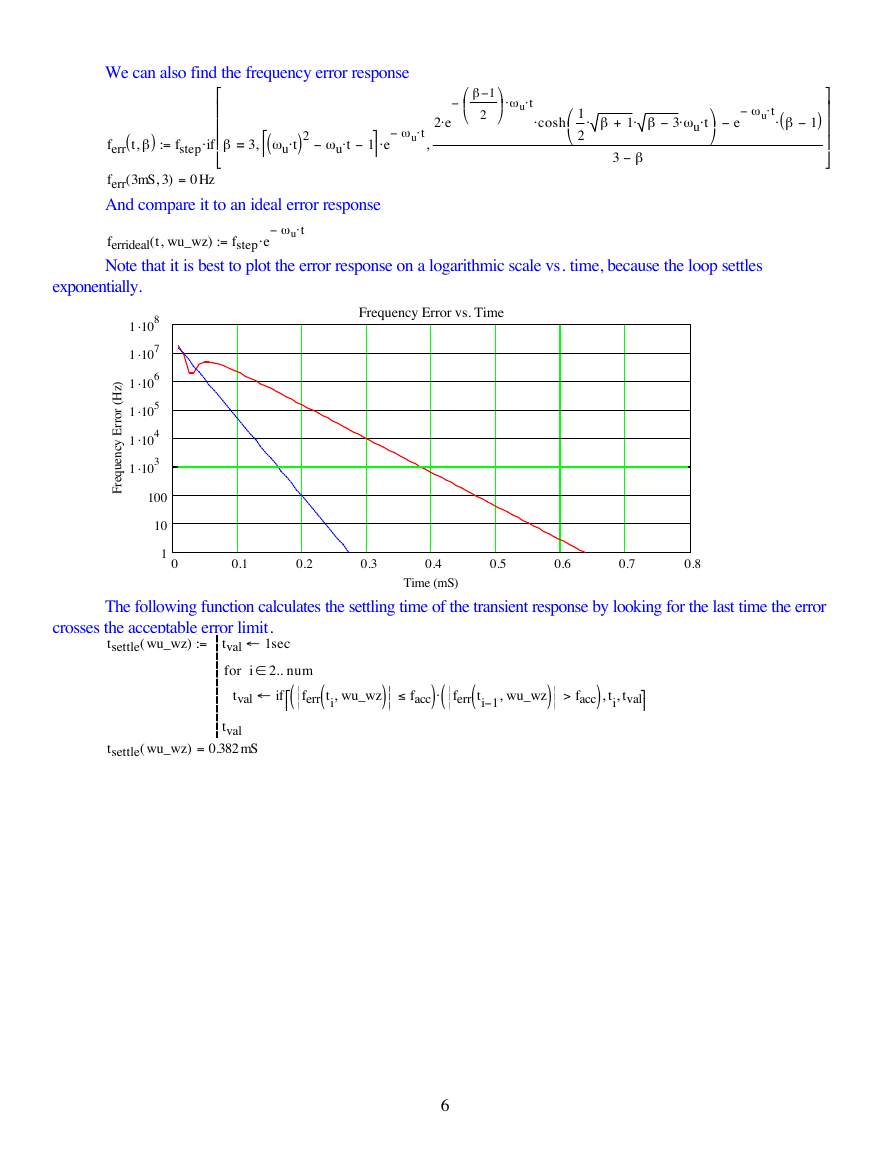
We can also find the frequency error response ( )2 ) := , 3= ferr t b,( ferr 3mS 3, ( ) And compare it to an ideal error response fstep if b = w u t w u t 0Hz 1- ß e 2 e w u t , 1- 2 w u t cosh 1 2 1+ 3 3- w u t w u t ( e ) 1- ,( := ferrideal t wu_wz ) Note that it is best to plot the error response on a logarithmic scale vs. time, because the loop settles fstep e w u t exponentially. ) z H ( r o r r E y c n e u q e r F 1 .108 1 .107 1 .106 1 .105 1 .104 1 .103 100 10 1 0 Frequency Error vs. Time 0.1 0.2 0.3 0.4 Time (mS) 0.5 0.6 0.7 0.8 The following function calculates the settling time of the transient response by looking for the last time the error ) facc ( ( ferr ti 1- , ) wu_wz ) facc > , , ti tval 6 crosses the acceptable error limit. tsettle wu_wz ) ( := tval i for tval 1sec 2 num.. if ( ) ferr ti wu_wz ,( tsettle wu_wz ) ( = tval 0.382mS - Ø º ø - b Ł ł - b b Ł ł - b - b - Ø Œ Œ Œ º ø œ œ œ ß - ‹ £ Ø º ø ß ‹ ˛

Now to visually find the optimum phase margin, we plot the settling time vs. phase margin. This is also useful for adding margin due to process variations b min := 1.5 b max 5:= ( b max ) b min + b min Settling Time vs. Phase Margin := numB 40 := .. 1 numB 1- := i i i numB 1- 0.8 0.6 0.4 0.2 ) S m i ( e m T g n i l t t e S 0 20 25 30 35 45 40 50 Phase Margin (deg) 55 60 65 70 The following function sweeps through values of wu_wz to find the optimal value. wu_wzopt 109sec := wu_wzopt = 2.846 tsetmin b opt for i 0 .. 1 numB 1- i numB 1- ( b max ) b min + b min tsettle tval i for tval 109sec 2 num.. ( if b,( ferr ti ) ) facc ( ( ferr ti 1- ) b, ) facc > , , ti tval tval < ( if tsettle ( if tsettle b opt tsetmin b opt b, tsetmin < tsetmin ) b opt , tsettle , , ) tsetmin This corresponds to a phase margin of PMopt We increase this phase margin slightly to account for loop gain variations. Note that this value will change when PM wu_wzopt 51.282deg PMopt := = ( ) slewing effects are added. 7 b - ‹ ‹ b - ‹ ‹ £ Ø º ø ß ‹ ˛ ‹ ‹ ‹ ˛

_______________________________________ Synthesis of Loop Filter Components With given values for w u, Kf , Kv, and N and now wu_wz, we can solve for the loop filter components. The equations which must be solved simultaneously are given below: w u = w u = Kv wu_wz Kf ) ( N C1 C2+ C1 C2+ 1 R1 C1 C2 wu_wz R1 C1 wu_wz = w u The solution to these three equations are the following loop filter components := C2 2 w u Kf Kv N := C1 := R1 Kf Kv 2 w u N w u N ( Kf Kv wu_wz wu_wz2 ( ) 1- wu_wz wu_wz2 wu_wz2 ) 1- = C2 0.02nF = C1 0.263nF = 225.64kW R1 If these equations are plugged back into the original transfer function, the expression simplifies to wu_wz 1+ s w u s GH s( ) := 1 wu_wz 2 + 1 s w u w u wu_wz We can use this to plot the magnitude and phase response for different values of wu_wz as shown in the following plots normalized to 1Hz. + AngleGH f_fu deg 180 := ( ) atan wu_wz f_fu ( ) atan f_fu wu_wz MagGH f_fu ( ) := 1 ( wu_wz f_fu )2 wu_wz f_fu ( )2 + 1 f_fu wu_wz 1+ 2 8 Ł ł - Ł ł - Ł ł

资料库

电荷泵锁相环mathcad设计文档.pdf

相关推荐

行业

热门标签

最新资料