第 27 卷 第 6 期 2002 年 12 月 昆 　明 　理 　工 　大 　学 　学 　报 Journal of Kunming University of Science and Technology Vol . 27 　No . 6 Dec. 2002 基于模型的预测控制算法研究 史红梅 ,冯丽辉 ,钟伟红 ,彭云峰 (昆明理工大学 信息工程与自动化学院 , 云南 昆明 　650051) 摘要 : 简要介绍了 MPC 算法 ,包括其理论 、优点及一些重要参数及选取. 然后根据两个具体模型 的传统 PID 控制算法实现和 MPC 控制算法实现 ,比较两种控制算法 ,分析 MPC 算法的一些重要 参数 ,得出 MPC 算法在稳定性和快速性方面的优点. 最后提到 MPC 算法在国内外的发展现状及 广阔前景. 关键词 : MPC ;有约束 MPC 控制器 ;模型预测控制工具箱 中图分类号 :TP273 文献标识码 :A 文章编号 :1007 - 855X(2002) 06 - 072 - 04 0 引 言[2 ,5 ] 预测控制通常称为基于模型的预测控制 (MPC) ,又叫模型预测控制 ,是目前应用最广泛的先进控制策 略. MPC 为了优化对象的未来行为 ,而计算一系列被控变量的调整. 是一种计算机优化控制算法 ,基本思 想容易理解 ,且作为一种高级控制技术 ,广泛地应用于工业过程. 模型预测控制产生于 20 世纪 70 年代 ,最 早由美国和法国几家公司先后提出 ,该算法直接产生于工业过程的实际应用 ,20 世纪 80 年代初开始真正 发展起来. 模型预测控制算法首次开发是为了满足电厂和石油冶炼的控制需要 ,但现在模型预测控制技术 的应用领域已经很广泛 ,包括精炼 、石油 、化工 、食物加工 、航空 、采矿 、冶金 、造纸以及公用事业等. 现代控制理论的特点是要求精确的模型 、最优的性能指标 、系统的设计方法. 而现代工业过程的特点 是多变量 、非线性 、时变性 、强耦合 、不确定性且要求高质量的控制性能 ,对模型要求高 ,还要实现方便. 显 然 ,现代控制理论在某些方面不能很好地满足现代过程工业的要求. 而预测控制的特点[ 5 ]是 : 对模型要求不高 ,不需要深入了解过程内部机理 ,建模方便 ; 鲁棒性可调 ,有利于提高系统的鲁棒性 ; 较好的动态控制效果 ; 可处理约束 ; 可实现多目标优化 (包括经济指标) ; 不增加理论困难 ,可推广到有约束条件 、大纯滞后 、非最小相位及非线性等过程. 针对现代控制理 论中的特点要求 ,考虑模型预测控制的特点. 模型预测控制是工业控制工程中必不可少的部分 ,正逐渐成 为先进控制应用软件的明智选择. 所以模型预测控制近年来 ,在控制界 ,尤其是过程工业方面蓬勃发展. 1 基本原理[1 ,2 ] 1978 年 ,J . Richalet 等提出了预测控制算法的三要素 :内部 (预测) 模型 、参考轨迹 、控制算法. 现在一 般则更清楚地表述为 :内部 (预测) 模型 、滚动优化 、反馈控制. 它的基本思想容易理解. 预测模型的功能就 是根据被控对象的历史信息和未来输入 ,预测系统未来输出 ,该模型只强调模型的功能而不强调其结构形 式. 模型预测控制算法本身是一种有限时段的优化控制算法. 不用对全局相同的优化指标 ,而是用相对于 每一时刻的该时刻的优化性能指标. 不是一次离线进行 ,而是反复在线进行的 ,即所谓滚动优化. 模型预测 控制的优化是基于每一时段的反馈信息. 所以 ,模型预测控制是一种建立在反馈信息基础上的反复决策过 收稿日期 :2002 - 05 - 16. 第一作者简介 :史红梅 (1978～) ,女 ,硕士研究生 ;主要研究方向 :模型预测控制及其应用. © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

第 6 期 　　　　　　　　　　史红梅 ,冯丽辉 ,等 :基于模型的预测控制算法研究 37 程. 虽然模型预测控制技术现在有好多种算法 ,例如 ,IMC ( Internal Model Control 内模控制) 、MAC (Model Algorithm Control 模型算法控制) 、DMC (Dynamic Matrix Control 动态矩阵控制) 、GPC ( General Predictive Control 广义预测控制 ) 、PFC (Predictive Function Control 预测函数控制) 等 ,但无论其算法形式多么不同 , 都建立在以上三项基本原理基础之上. 2 控制时域 M 、预测时域 P、误差加权矩阵 Q 和控制加权矩阵λ的选择[ 1 , 2] 多步预测控制律选用含有对控制量加权的二次型性能指标 : 　　　　　J P = P i = 1 qi [ y P ( k + i) - y r ( k + i) ]2 + M j = 1 λi [ u ( k + j - 1) ]2 式中 　 P ———预测时域长度 ; M ———控制时域长度 ; q1 ———多步预测输出误差的加权系数 ; λ1 ———多步预测输出控制量的加权系数. 对应上式可以看出 , P 表示我们对 k 时刻起未来多少步的输出逼近期望值感兴趣. 为了使动态优化真 正有意义 ,要求优化的范围应该是对象的真实动态部分. 所以 ,优化时域 P 必须超过对象阶跃响应的时滞 部分 ,或由非最小相位特性引起的反向部分 ,并覆盖对象动态响应的主要部分. 适当减小 P 可以提高快速 性 ,适当增大 P 可以增加稳定性. 控制时域 M 在式中表示了所要确定的未来控制量改变的数目. 由于优化主要针对未来 P 各时刻的输 出误差进行的 ,它们至多只受到 P 各控制增量的影响 ,所以从物理上应该规定 M ≤ P. 实践表明 ,许多情 况下 ,增大 (减小) P 和减小 (增大) M 有着类似的效果. 误差加权矩阵 Q 大小反映了在优化性能指标中不同时刻对输出预测值逼近期望值的重视程度 ,决定 了响应误差项在优化指标中所占的比重. 一般选为对角阵 ,但要具体情况具体分析. 控制加权矩阵λ的作 用是限制控制增量的剧烈变化 ,减少对系统的过大冲击.λ大时 ,闭环动态响应缓慢 ,所以一般较小. 总之 ,以上所述只是理论原则 ,针对具体系统要反复试凑和仿真 ,才能最终达到满意效果. 下面在 MATLAB 环境中 ,针对具体模型进行分析. 3 实例比较 本文所用仿真模拟语言工具为美国 MathWorks 公司的 MATLAB 6. 1 版. MATLAB 语言 MPC Toolbox 中提供了基于动态矩阵控制算法的函数 cmpc ( ) . 动态矩阵控制算法 (DMC) 采用工程上易于获取的对象 阶跃响应模型 ,算法较简单 ,计算量较少 ,鲁棒性较强 ,适用于纯时延 ,开环渐进稳定的非最小相位系统 ,在 工业过程控制中得到成功应用. 本文采用的即是 cmpc ( ) ,其功能是设计于仿真输入输出受限的模型预测 控制器. 所谓输入输出受限就是指系统的输入输出变量满足一定的上下界要求. 下面通过两个具体实例 (例子中各参数的选择 ,在程序中经反复试凑和调试已经给出) ,对传统 PID 算法控制和 MPC 算法控制进 行比较. 3. 1 模型 Ⅰ 模型 Ⅰ的带 PID 控制器的模型方框图如图 1 所示. 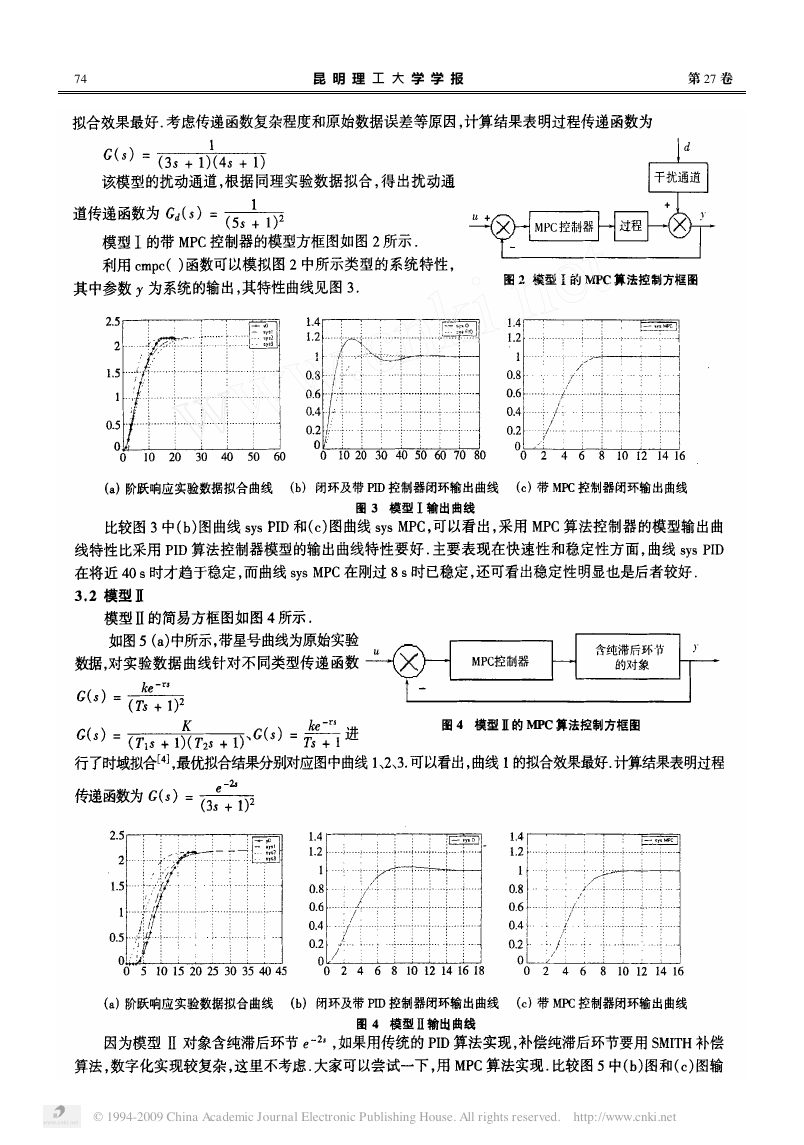如图 3 (a) 中所示 ,带星号曲线为原始实验数据 ,对实验数 据曲线针对不同类型传递函数 : G ( s) = K ( T1 s + 1) T2 s + 1) 、 G ( s) = K ( Ts + 1) 2 、G ( s) = Ke - τs Ts + 1 进行了时域拟合[4 ] ,最优拟 合结果分别对应图中曲线 sys1 、sys2 、sys3. 可以看出 ,曲线 1 的 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

47 昆 明 理 工 大 学 学 报 　　　　　　　　　　　　　　　　　第 27 卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

2 第 6 期 　　　　　　　　　　史红梅 ,冯丽辉 ,等 :基于模型的预测控制算法研究 57 出曲线 ,我们可以看出 ,在对有纯延迟的模型的控制方面 ,模型预测控制算法比传统的 PID 控制算法要好. 快速性和稳定性都较好 ,而且明显的一点是能明确的表示出系统的纯滞后. 由以上二者比较可知 ,MPC 算法比 PID 算法控制更有力 ,稳定性 (鲁棒性) 和动态特性方面前者优于 后者. 所以 ,MPC 控制将会有很大的发展空间. 4 结束语 由于模型预测控制特别适合现代控制发展的要求 ,有着其他控制算法所不可比拟的优点 ,所以国内外 的各大控制公司和科研机构都纷纷把目光聚向了模型预测控制. 国外优秀软件主要有 AspenTech 公司的 DMCplus 、Honeywell 公司的 PCT ( Precictive Control Technoloty) 和 RMPC ( Robust Model Predictive Control ) 、 Adersa 公司的 PFC (Predictive Function Control) 、Setpoint 公司的 IDCOM M (Multivariable Identification and Command) 等. 较新的是 DMCplus ,一种动态矩阵控制软件 ,是由 AspenTech 公司收购了 DMC 公司 (Dynamic Matrix Control Corporation) 和 Setpoint 公司后开发的“新一代”多变量控制产品. DMCplus 继承了由这些公司 以前在 1 000 多个控制应用软件中所采用的技术. 与国外相比 ,国内优秀预测控制软件相对较少 ,发展较为落后 ,主要有国产多变量约束控制软件包 MCC (Multivariable Constrained Control) 、多变量预测控制软件 RMPC (Robust Multivariable Predictive Control) 等. 国产多变量约束控制软件包 MCC 由多变量约束预测控制器 、非线性预测控制器 、过程模型辨识软件 包 、组态软件包 、系统动态仿真软件包 、数据及图形处理软件包 、过程和模型参数在线校正软件包 、MCC 与 各类 DCS 的接口软件包等部分组成. 多变量预测控制软件 RMPC 是以国家“九五”项目为依托 ,由中国科 学院自动化研究所综合自动化技术工程研究中心开发的一套鲁棒多变量预测控制软件包 (已通过国家“九 五”项目验收) . 具有辨识 、鲁棒控制 、经济指标优化 、仿真等功能 ,面向多种工业过程 ,适用范围广 ,已成功 应用于山东省三孔啤酒有限公司. 由上可知 ,模型预测控制在现代工业控制中有广阔的发展前景 ,而我国在这方面的研究和开发还不是很 成熟. 但这也说明 ,国内还有更大的发展空间 ,和更大的市场 ,所以在此领域还有很多工作需要做. 考虑模型 预测控制的发展方向和工业应用的前景 ,主要是以下几个发展方向[5 ] :多变量预测控制系统鲁棒性的深入研 究 ;实际工业中非线性系统普遍存在 ,非线性预测控制系统亟待开发 ;致力于实用性较强的 ,和高的性能软件 工具的开发和研究 ;因为在一个单独的目标函数中 ,表示出所有相关控制对象很难 ,下一代的模型预测控制 技术将有可能采用多目标函数 ;无限预测域具有有利的理论特性 ,也将会成为一种标准指标. 参考文献 : [1 ] 席裕庚. 预测控制[M ]. 北京 ;国防工业出版社 ,1993 ,10～18. [2 ] 舒迪前. 预测控制系统及其应用[M ]. 北京 :机械工业出版社 ,1996 ,127～173. [3 ] 徐昕 ,李涛 ,伯晓晨. MATLAB 工具箱应用指南 —控制工程篇[M ]. 北京 :电子工业出版社 ,2000. 229～254. [4 ] 陈浩 ,刘中仁 ,吴浚郊. 模糊控制在型沙质量控制中的应用研究[J ]. 自动化与仪表 ,1999 , (6) :10～12. [ 5 ] S.Joe Qin , Thomas A. Badgwell An Overview of Industrial Model Predictive Control Technology[J ]. Computer Based Learning Unit , University of Leeds , English ,1996. MPC Algorithm Research Based on Models SHI Ho ng mei ,FEN G Li hui ,ZHON G Wei ho ng ,PEN G Yun f e ng (Faculty of Information Engineering and Automation , Kunming University of Science and Technology , Kunming 650051 ,China) Abstract : At first , MPC algorithm is briefly talked about , including its basic theory , advantages to other algo rithms and the choosing of some key parameters. Then based on two practical models , among which one adopts traditional PID control algorithm and the other adopts MPC algorithm , several key parameters are analyzed and some advantages of MPC algorithm on stability and quick response ability are concluded. Finally , the develop ment status and prospect of MPC , home or abroad , are mentioned. Key words : MPC ; constrained MPC controller ; MATLAB MPC toolbox © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net