数学建模自习室开放的优化管理论文.doc-资料库

panyan861110-1938443-16359647628688129816.doc.pdf-第1页.png

第1页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第2页.png

第2页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第3页.png

第3页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第4页.png

第4页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第5页.png

第5页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第6页.png

第6页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第7页.png

第7页 / 共9页

panyan861110-1938443-16359647628688129816.doc.pdf-第8页.png

第8页 / 共9页

自习教室开放的优化管理摘要：本文针对某校提供的数据及要求，对该校自习教室的开放做了一个合理的规划安排。在问题（1）中，学校估计每个学生上自习的可能性为 0.7，而且要使需要上自习的同学的满意度不能低于 95%，通过二项分布可知道学校 8000 名学生中至少期望 5320 人能上自习。又根据该校开放教室满座率的要求，我们通过建立 0—1 目标规划模型，通过 lingo 软件工具包编程运行得到最优方案为：***此时的用电情况为：***上自习的学生总人数为：*** 基本满足该校节约用电和期望数量的学生都有座位上自习，而且达到其满意度的要求。在问题（2）中，由于加入了学生宿舍分区和教室分区距离的因素，学生上自习的满意度因路程的远近会有所不一样。所以，关键字：0—1 目标规划二项分布 1.问题重述近年来，大学用电浪费比较严重，集中体现在学生上晚自习上，一种情况是去某个教室上自习的人比较少，但是教室内的灯却全部打开，第二种情况是晚上上自习的总人数比较少，但是开放的教室比较多，这要求我们提供一种最节约、最合理的管理方法。现根据某学校收集的部分数据（见附件 1 中附表 1），管理人员只需要每天晚上开一部分教室供学生上自习，每天晚上从 7：00---10：00 开放（如果哪个教室被开放，则假设此教室的所有灯管全部打开）。完成以下问题：（1）假如学校有 8000 名同学，每个同学是否上自习相互独立，上自习的可能性为 0.7. 要使需要上自习的同学满足程度不低于 95%，开放的教室满座率不低于 4/5，同时尽量不超过 90%。问该安排哪些教室开放，能达到节约用电的目的. （2）假设这 8000 名同学分别住在 10 个宿舍区，现有的 45 个教室分为 9 个自习区，按顺序 5 个教室为 1 个区，即 1,2,3,4,5 为第 1 区，…，41,42,43,44,45 为第 9 区。这 10 个宿舍区到 9 个自习区的距离见附件 1 中附表 2。学生到各教室上自习的满意程度与到该教室的距离有关系，距离近则满意程度高，距离远则满意程度降低。假设学生从宿舍区到一个自习区的距离与到自习区任何教室的距离相同。请给出合理的满意程度的度量，并重新考虑如何安排教室，既达到节约用电目的，又能提高学生的满意程度。另外尽量安排开放同区的教室。（3）假设临近期末，上自习的人数突然增多，每个同学上自习的可能性增大为 0.85， 1

要使需要上自习的同学满足程度不低于 99%，开放的教室满座率不低于 4/5，同时尽量不超过 95%。这时可能出现教室不能满足需要，需要临时搭建几个教室。假设现有的 45 个教室仍按问题 2 中要求分为 9 个区。搭建的教室紧靠在某区，每个区只能搭建一个教室，搭建的教室与该区某教室的规格相同（所有参数相同），学生到该教室的距离与到该区任何教室的距离假设相同。问至少要搭建几个教室，并搭建在什么位置，既达到节约用电目的，又能提高学生的满意程度. 2.问题的分析该问题是在满足约束条件的要求下的自习室最优化管理的问题，而在问题中的影响因素学生的人数是不确定的，每个学生上不上自习也是波动的。在问题（1）中，只要考虑学生的满意度和每个教室的满座率两个影响因素，求解最优的开放方案。因此，本问题可以建立 0—1 规划模型，使得目标函数在满足约束条件的情况下求解最优解。在问题（2）中，加上了学生分区和教室分区，每个宿舍区到教室区的距离不同，而学生的的满意度就会受到距离的影响。问题中给出总共有 8000 名学生， 3.模型的假设及符号说明 3.1 模型假设（1）开放上午所有教室的灯管都在同一时间开、关；（2）所有教室的灯管都完好无损，均能正常工作；（3）所有上自习的学生均从 7 点上到 10 点，及如果 A 同学上了一半自习离开后 B 同学有来坐同一个座位；（4）所有同学都有相同的上自习欲望，不考虑路程带给学生的心理影响；（5）不考虑有的同学由于一些原因而无法上自习的情况，例如生病，请事假等；（6）所有教室的座位完好无损； 3.2 符号说明模型Ⅰ： i：表示教室号，且 i=1，2，…，45； 2

xi：表示对第 i 个教室的开放情况； wi：表示第 i 间教室开放时所消耗的电功率； wi’：表示第 i 间教室里每根灯管的功率； ti：表示第 i 间教室里的灯管数； W：表示开放自习室时消耗的总的电功率； yi：表示第 i 间教室的座位数； ni：表示去第 i 间教室上自习的学生人数； N：表示总的学生人数； p：表示每个同学上自习的可能性； q：表示上自习的同学的满意程度 r：表示教室的满座率上限率； r’：表示教室的满座率下限率； 4.模型建立与求解 4.1 模型建立模型Ⅰ：对于问题（1），对于开放教室设置变量： ix 1  ，开放第教室   0  ，不开放第各教室 i i 开放的自习室所消耗的所有电功率 W 为： W= x w *i i 45 i=1 ……………(1) 每间教室的可以容纳的人数约束： n  i   n i '* y r i * r y i * ; x i * . x i ……………(2) 上自习的同学有对教室的安排的满意程度，因此有一个学生满意程度约束：自然约束： 45  i 1  * * x n N p q i *  i ……………(3) 3

 45; 0,1; 1,2,...,45. 45   x  i   1 i  x i   i  ……………(4) 在满足（2）（3）（4）的约束下求解 W 取得最小值是的最优方案。模型Ⅱ： 4.2 模型求解：首先，根据模型可知道目标函数为： min W= 45 x w *i i i=1 ……………(1*) 在目标函数中，xi 为未知量，题中没有给出 wi 的值，但是每个教室的灯管数 ti 和该教室里灯管的功率 wi’为已知量，故每间教室开放时的消耗的总功率就可以算出来了。即 '* w w t i  i ，根据题中所给数据解得 wi 的值如表 1 所示： i 表 1 个教室总功率表教室号总功率教室号总功率教室号总功率教室号总功率教室号总功率 2304 2304 2500 2304 2500 2304 2304 1250 2160 1620 1620 1728 1620 1440 1620 1080 3375 2304 2500 2304 2500 1440 1620 1080 3375 2304 2500 1680 1680 2400 2400 1620 1620 1728 1620 1440 1620 1080 3375 2304 2500 1680 1680 2400 2400 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 4 45 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 问题要求开放的教室满座率不低于 4/5 ，同时尽量不超过 90% ，即 r=90% ， r’=4/5*100%=80%；所以约束条件（2）试为： n n    i i   *8.0 *9.0 y y i i ;* x i .* x i ……………(2*) 4

又由题意可知 N=8000，p=0.7，q=95%，所以 N*p*q=8000*0.7*95%=5320，即（3）试可转换为： 45  i 1  * x n i i  5320 ；……………(3*) 即在满足（2*）（3*）（4）约束条件下求解 0—1 变量 xi 使得目标函数达到最小。运用 lingo 软件工具包对模型Ⅰ编程求解，运行程序见附件 2 中 Model 1。运行的结果为： X(1)= X(2)= X(7)= X(9)= X(10)= X(15)= X(25)= X(33)= X(44)= X(45)=0 X(3)= X(4)= X(5)= X(6)= X(8)= X(11)= X(12)= X(13)= X(14)= X(16)= X(17)= X(18)= X(19)= X(20)= X(21)= X(22)= X(23)= X(24)= X(26)= X(27)= X(28)= X(29)= X(30)= X(31)= X(32)= X(34)= X(35)= X(36)= X(37)= X(38)= X(39)= X(40)= X(41)= X(42)= X(43)=1 即是说，为了尽量节约用电，我们现在对已有的 45 间教室开放教室号分别为：3、4、5、 6、8、11、12、13、14、16、17、18、19、20、21、22、23、24、26、27、28、29、30、31、 32、34、35、36、37、38、39、40、41、42、43 的教室，此时用电功率总共为 74777（w）；而对 1、2、7、9、10、15、25、33、44、45 号教室不开放。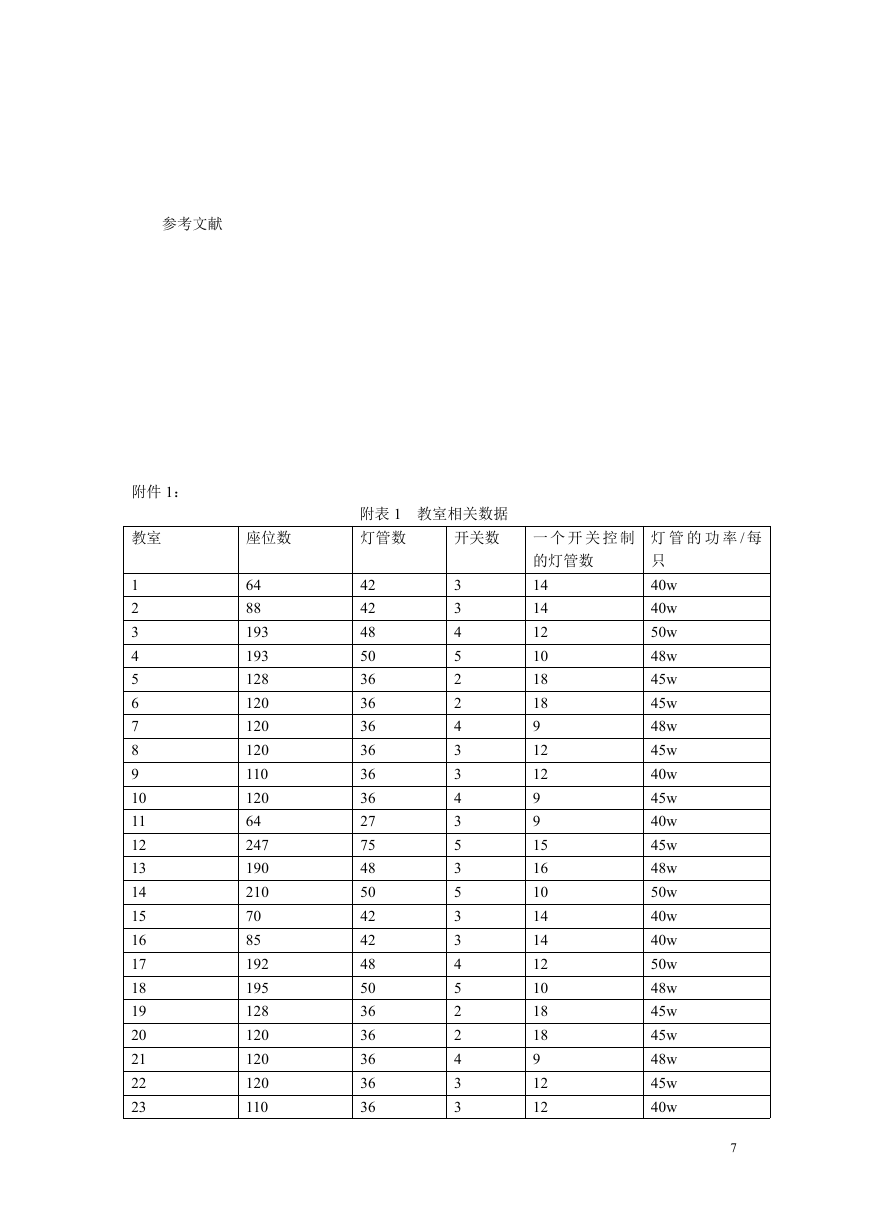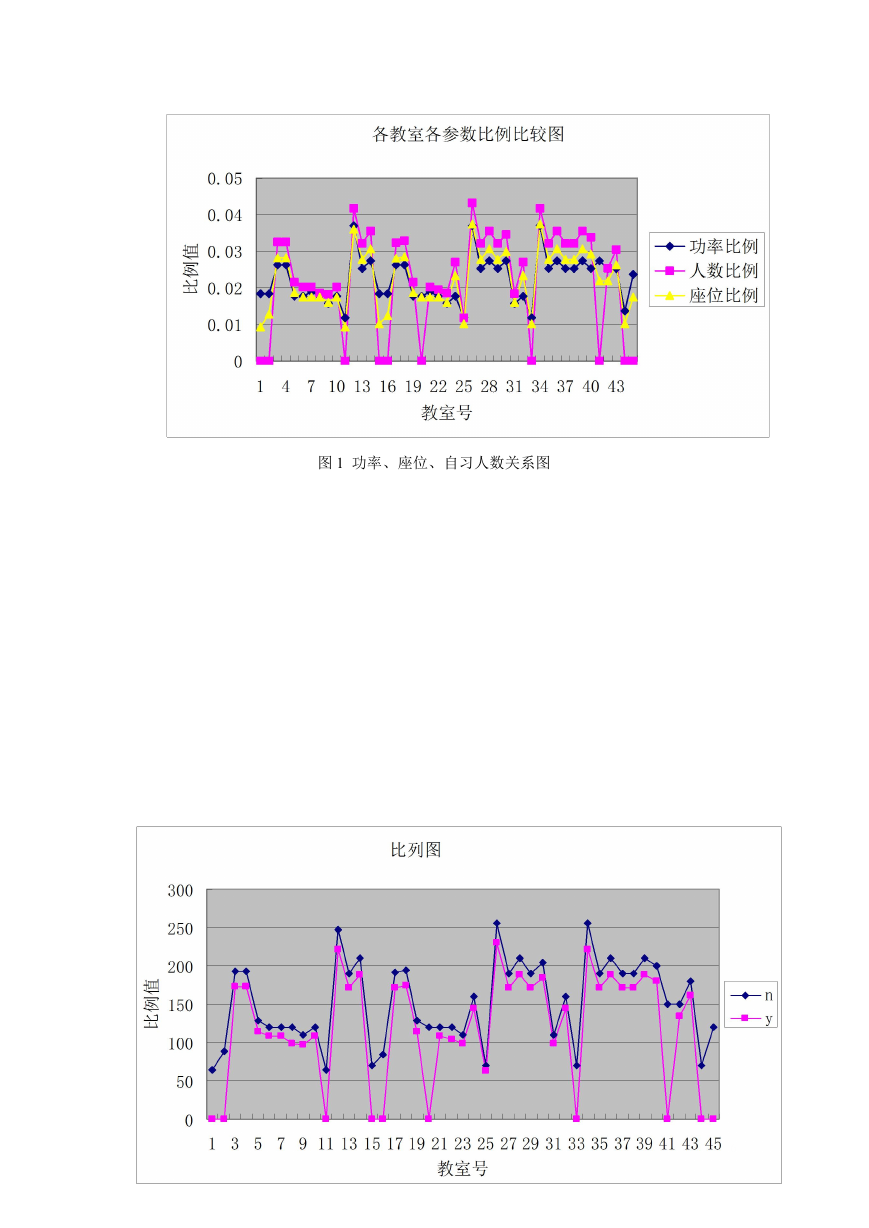 5.模型的结果分析与评价为了进一步分析，我们将每间教室的座位数、总功率、到该教师上自习的学生人数分别作以下处理， a i  y i 45  i 1  ； b i  y i n i 45  n i i 1  ； c i  w i 45  w i i 1  ；得到关于功率、座位、自习人数的三组比例数据，他们的关系如图 1 所示： 5

图 1 功率、座位、自习人数关系图 6

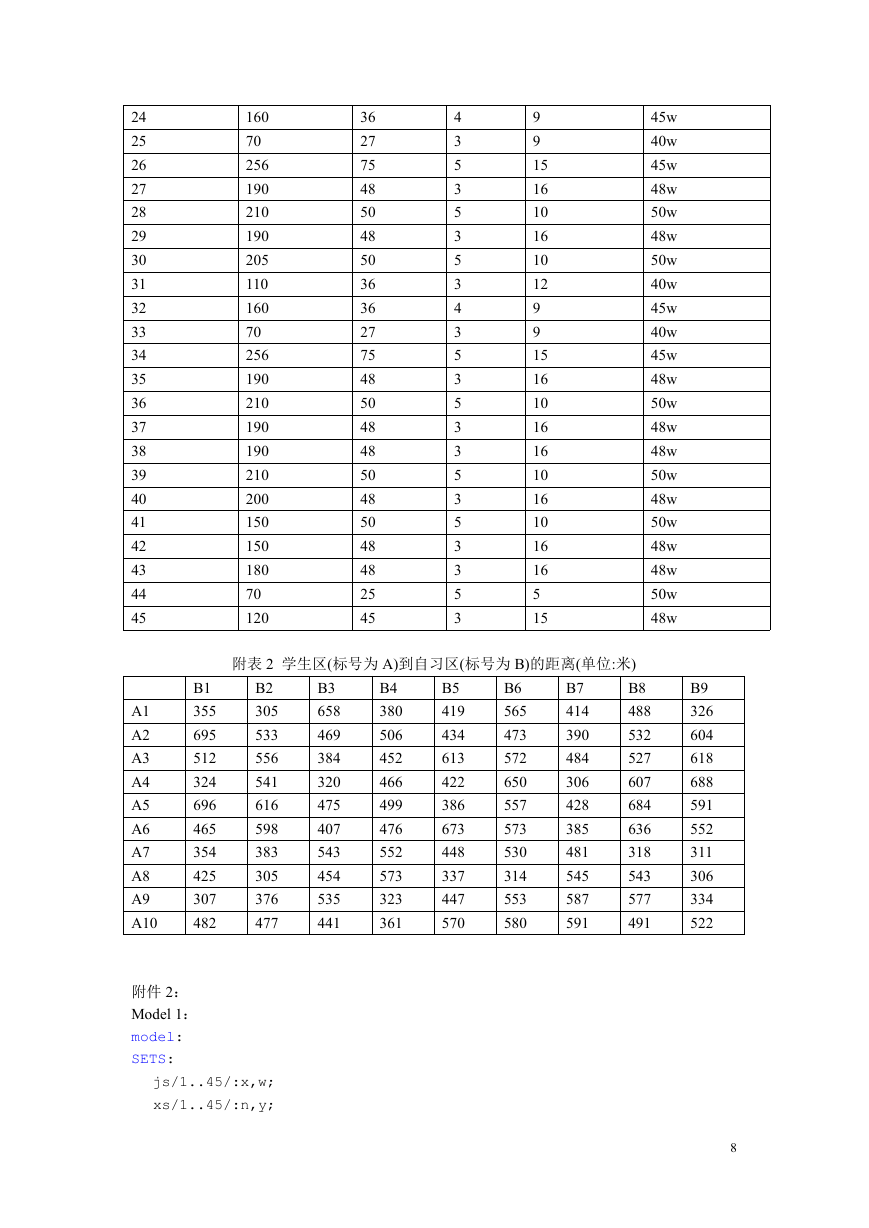
参考文献附件 1：教室座位数附表 1 教室相关数据开关数灯管数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 64 88 193 193 128 120 120 120 110 120 64 247 190 210 70 85 192 195 128 120 120 120 110 42 42 48 50 36 36 36 36 36 36 27 75 48 50 42 42 48 50 36 36 36 36 36 3 3 4 5 2 2 4 3 3 4 3 5 3 5 3 3 4 5 2 2 4 3 3 一个开关控制的灯管数 14 14 12 10 18 18 9 12 12 9 9 15 16 10 14 14 12 10 18 18 9 12 12 灯管的功率 / 每只 40w 40w 50w 48w 45w 45w 48w 45w 40w 45w 40w 45w 48w 50w 40w 40w 50w 48w 45w 45w 48w 45w 40w 7

24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 B1 355 695 512 324 696 465 354 425 307 482 160 70 256 190 210 190 205 110 160 70 256 190 210 190 190 210 200 150 150 180 70 120 36 27 75 48 50 48 50 36 36 27 75 48 50 48 48 50 48 50 48 48 25 45 4 3 5 3 5 3 5 3 4 3 5 3 5 3 3 5 3 5 3 3 5 3 9 9 15 16 10 16 10 12 9 9 15 16 10 16 16 10 16 10 16 16 5 15 45w 40w 45w 48w 50w 48w 50w 40w 45w 40w 45w 48w 50w 48w 48w 50w 48w 50w 48w 48w 50w 48w 附表 2 学生区(标号为 A)到自习区(标号为 B)的距离(单位:米) B8 488 532 527 607 684 636 318 543 577 491 B4 380 506 452 466 499 476 552 573 323 361 B5 419 434 613 422 386 673 448 337 447 570 B6 565 473 572 650 557 573 530 314 553 580 B7 414 390 484 306 428 385 481 545 587 591 B2 305 533 556 541 616 598 383 305 376 477 B3 658 469 384 320 475 407 543 454 535 441 附件 2： Model 1： model: SETS: js/1..45/:x,w; xs/1..45/:n,y; B9 326 604 618 688 591 552 311 306 334 522 8

资料库

数学建模自习室开放的优化管理论文.doc

相关推荐

课程资源

热门标签

最新资料