AUCSC 210 Algorithm Analysis and Data Structures Programming Assignment 1: Infix Expression Evaluation Due date: Oct. 8 (by midnight) Objectives • To gain understanding of how an implementation of an ADT is used by an application program. • To learn how expressions can be evaluated at run-time. • To become familiar with how infix expressions can be converted to postfix expressions. Assignment Write a Java program (a collection of Java classes), including a class named InfixExpressionEvaluator that contains a static main method. This main method will prompt the user to enter a constant expression (i.e., a mathematical expression without variables) at the keyboard. The expression must be in infix notation and must use spaces to separate the tokens (operands and operators) of the expression. (This restriction is imposed to simplify the parsing of the input.) The only exception to the space-separation rule is for the unary minus prefix operator, which will be assumed to be part of the specification of a negative constant operand. The program will then evaluate the expression and display the result on the console. It will then wait for another expression to be entered for evaluation, terminating on an empty input. 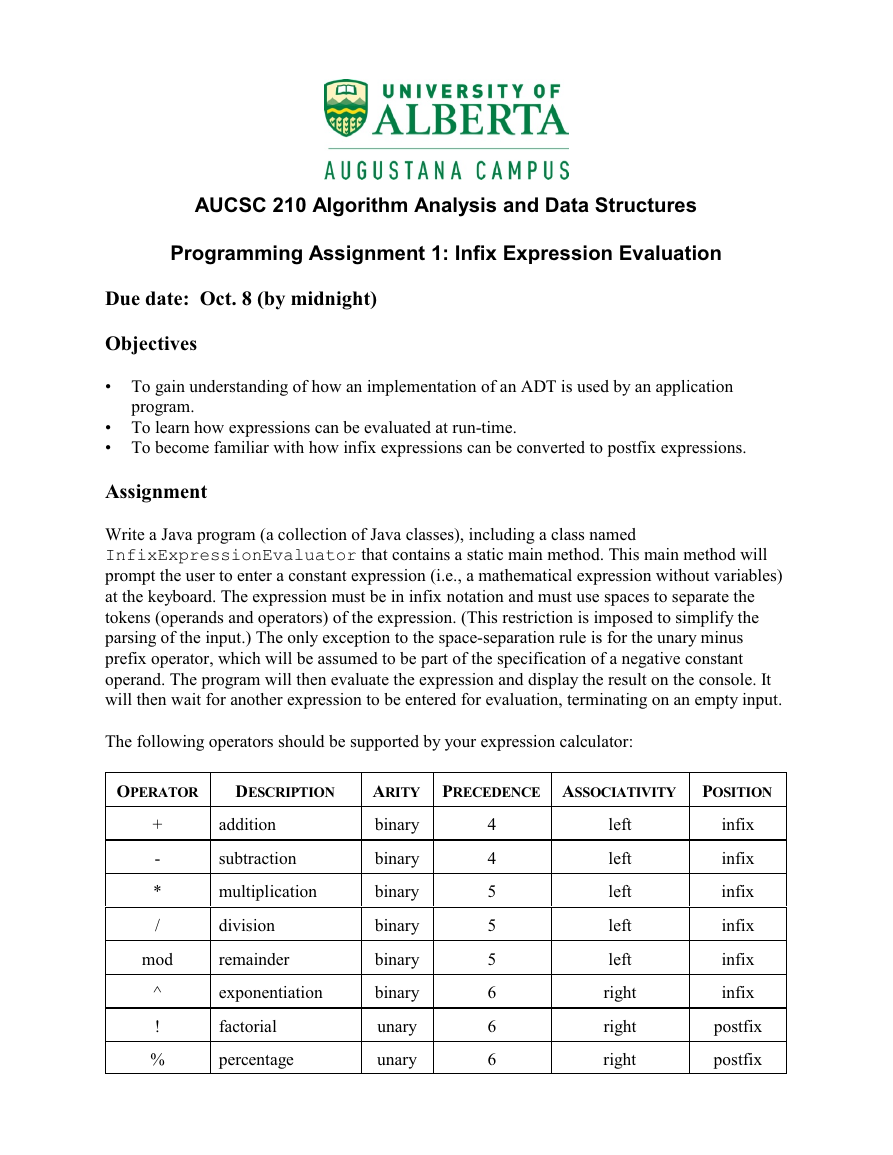The following operators should be supported by your expression calculator: OPERATOR DESCRIPTION + - * / mod ^ ! % addition subtraction multiplication division remainder exponentiation factorial percentage ARITY binary binary binary binary binary binary unary unary PRECEDENCE ASSOCIATIVITY POSITION 4 4 5 5 5 6 6 6 left left left left left right right right infix infix infix infix infix infix postfix postfix 

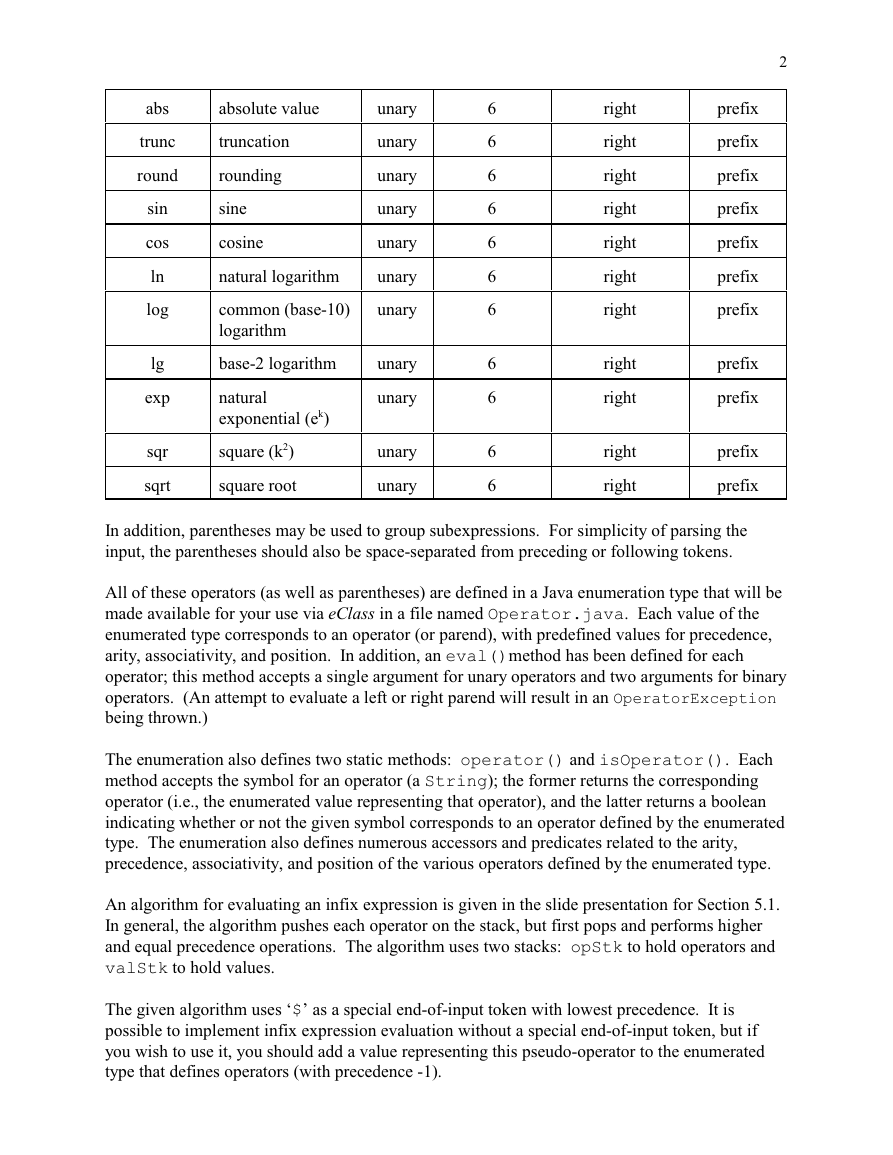
abs trunc round sin cos ln log lg exp sqr sqrt absolute value truncation rounding sine cosine natural logarithm common (base-10) logarithm base-2 logarithm natural exponential (e )k square (k ) 2 square root unary unary unary unary unary unary unary unary unary unary unary 6 6 6 6 6 6 6 6 6 6 6 2 prefix prefix prefix prefix prefix prefix prefix prefix prefix prefix prefix right right right right right right right right right right right In addition, parentheses may be used to group subexpressions. For simplicity of parsing the input, the parentheses should also be space-separated from preceding or following tokens. All of these operators (as well as parentheses) are defined in a Java enumeration type that will be made available for your use via eClass in a file named Operator.java. Each value of the enumerated type corresponds to an operator (or parend), with predefined values for precedence, arity, associativity, and position. In addition, an eval()method has been defined for each operator; this method accepts a single argument for unary operators and two arguments for binary operators. (An attempt to evaluate a left or right parend will result in an OperatorException being thrown.) The enumeration also defines two static methods: operator() and isOperator(). Each method accepts the symbol for an operator (a String); the former returns the corresponding operator (i.e., the enumerated value representing that operator), and the latter returns a boolean indicating whether or not the given symbol corresponds to an operator defined by the enumerated type. The enumeration also defines numerous accessors and predicates related to the arity, precedence, associativity, and position of the various operators defined by the enumerated type. An algorithm for evaluating an infix expression is given in the slide presentation for Section 5.1. In general, the algorithm pushes each operator on the stack, but first pops and performs higher and equal precedence operations. The algorithm uses two stacks: opStk to hold operators and valStk to hold values. The given algorithm uses ‘$’ as a special end-of-input token with lowest precedence. It is possible to implement infix expression evaluation without a special end-of-input token, but if you wish to use it, you should add a value representing this pseudo-operator to the enumerated type that defines operators (with precedence -1). 

The pseudocode for the algorithm as given in the slides is: Algorithm doOp() x 7 valStk.pop(); y 7 valStk.pop(); op 7 opStk.pop(); valStk.push( y op x ) 3 Algorithm repeatOps( refOp ): while ( valStk.size() > 1 ^ prec(refOp) # prec(opStk.top()) doOp() Algorithm EvalExp() Input: a stream of tokens representing an arithmetic expression (with numbers) Output: the value of the expression while there’s another token z if isNumber(z) then else valStk.push(z) repeatOps(z); opStk.push(z) repeatOps($); return valStk.top() Note that this algorithm does not work correctly for right-associative operators such as ‘^’. The expression 2 ^ 3 ^ 4 should evaluate as 2 ^ (3 ^ 4), not as (2 ^ 3) ^ 4. You will have to adjust the algorithm so that it correctly evaluates expressions including right-associative operators. Hint Use Java’s StringTokenizer or the Scanner class of Java 5 (and later versions) to parse expressions. The latter offers the methods hasNextType and nextType (where Type is replaced by Integer, Double, etc.), which would be convenient for checking if the next token in an expression can be parsed as a Double and is thus an operand. Submission Use the assignment submission form that will be provided in eClass to submit your solution to this assignment. It would be preferred if you submitted your code as a NetBeans project in a ZIP file, but an Eclipse project or a collection of Java source files (‘*.java’) in a ZIP archive will be acceptable. Late submissions will be assessed a penalty of 1% per hour or portion of an hour.