1D_YEE_FDTD_MATLAB.doc

发布时间：2022-06-10 发布人：admin 分类：说明书资料大小：16.03M 资料格式：doc 举报版权申诉

m0_37747983-9865039-16359647492322207876.doc.pdf-第1页.png

第1页 / 共6页

m0_37747983-9865039-16359647492322207876.doc.pdf-第2页.png

第2页 / 共6页

m0_37747983-9865039-16359647492322207876.doc.pdf-第3页.png

第3页 / 共6页

m0_37747983-9865039-16359647492322207876.doc.pdf-第4页.png

第4页 / 共6页

m0_37747983-9865039-16359647492322207876.doc.pdf-第5页.png

第5页 / 共6页

m0_37747983-9865039-16359647492322207876.doc.pdf-第6页.png

第6页 / 共6页

文本预览

一、写出此程序的数学物理公式；答：（1）Gaussian pulse: （2）迭代公式： Project 1 一维YEE-FDTD )( tEi  exp(  (4 t  t  2  2 )) 0 (20分) E n X 1  )( k  n )( kE x  2/1  H n y )2/1  H n y 2/1  ( k  ))2/1 H n y 2/1  ( k  )2/1  H n y 2/1  )2/1  ( n ( kE x  )2/1  n ( kE x  ))2/1 ( dtc dz ( k  ( k  dtc dz 二、画出程序中所加源的随时间变化的曲线，并编程考察其频谱特性，给出代码；（20分）答：由高斯脉冲公式 2 0 )( tEi  exp(  (4 t  t  2  )) Ex(numCells/2) = exp(-0.5*((t0-t)/spread)^2)；程序可得，所以 5.0 spread  2 4  2  =60.16, 2/=0.033 故采样频率最小要大于0.07，下列程序中采样频率Fs取1。 2  ，其中 5.0 spread  2 4  2  程序如下： clear all close all % Gaussian pulse parameters t0 = 40; spread = 12; fs=1; N=1000; t=0:1/fs:N/fs; g=exp(-0.5*((t0-t)/spread).^2); % Hard source subplot(2,1,1) plot(t(1:200),g(1:200)); grid; xlabel('t');ylabel('Ei(t)');title('时域波形'); Y=fft(g,N); Y1=abs(Y); f=(0:N)*fs/N; subplot(2,1,2) plot(f(1:200),Y1(1:200)); grid; xlabel('f');ylabel('|Ei(f)|');title('频域波形'); %Center of pulse % Width of pulse %采样频率大于两倍频宽 %采样点数 %时间范围及步进 %first %时域信号 %快速傅里叶 %频率取幅度 %横轴频率范围 %second %频域信号

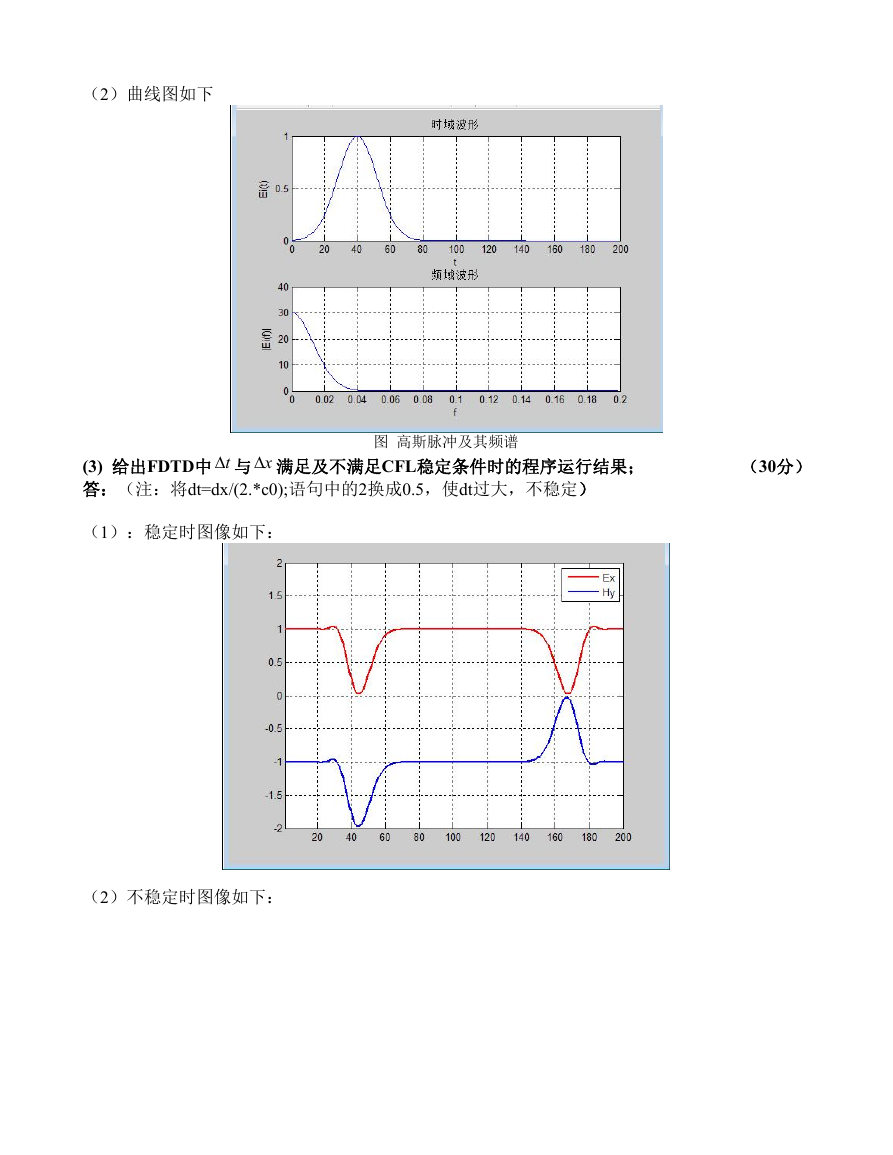
（2）曲线图如下 (3) 给出FDTD中 t 与 x 满足及不满足CFL稳定条件时的程序运行结果；答：（注：将dt=dx/(2.*c0);语句中的2换成0.5，使dt过大，不稳定）（30分）图高斯脉冲及其频谱（1）：稳定时图像如下：（2）不稳定时图像如下：

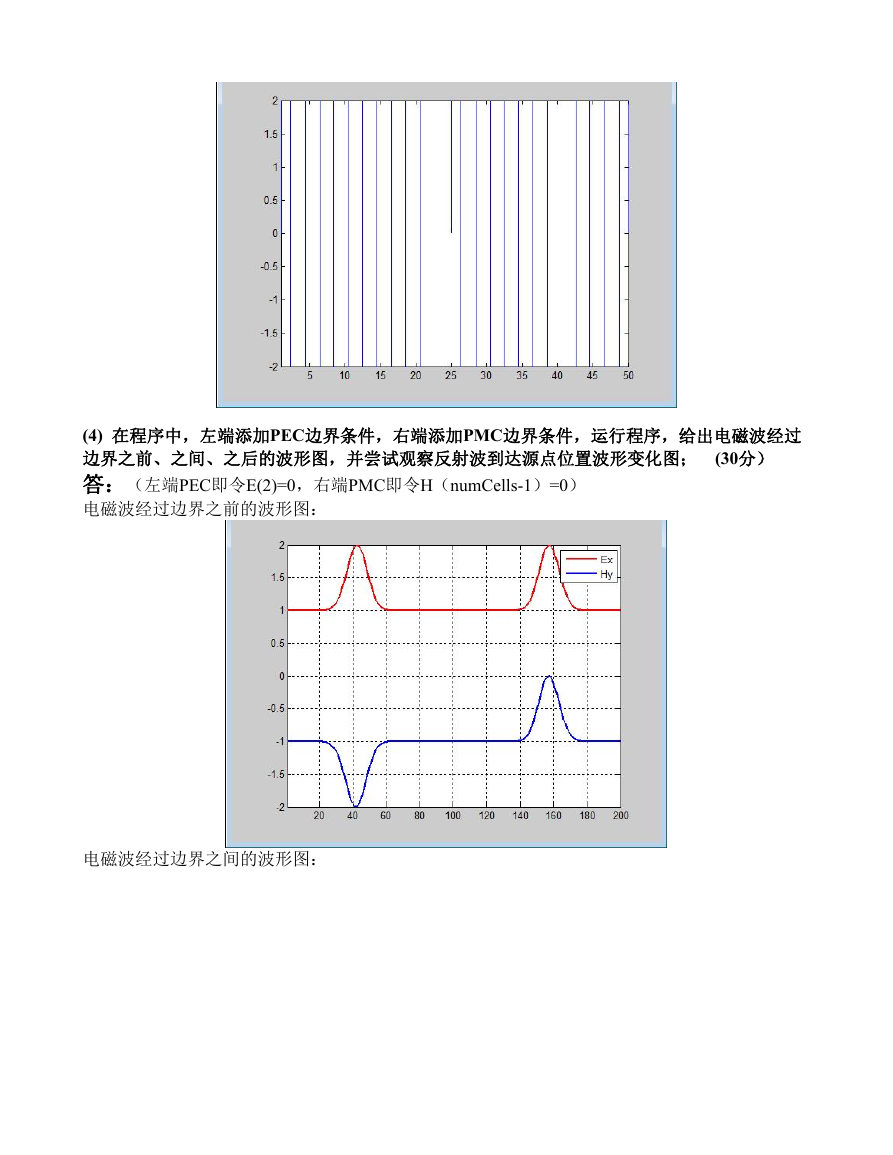
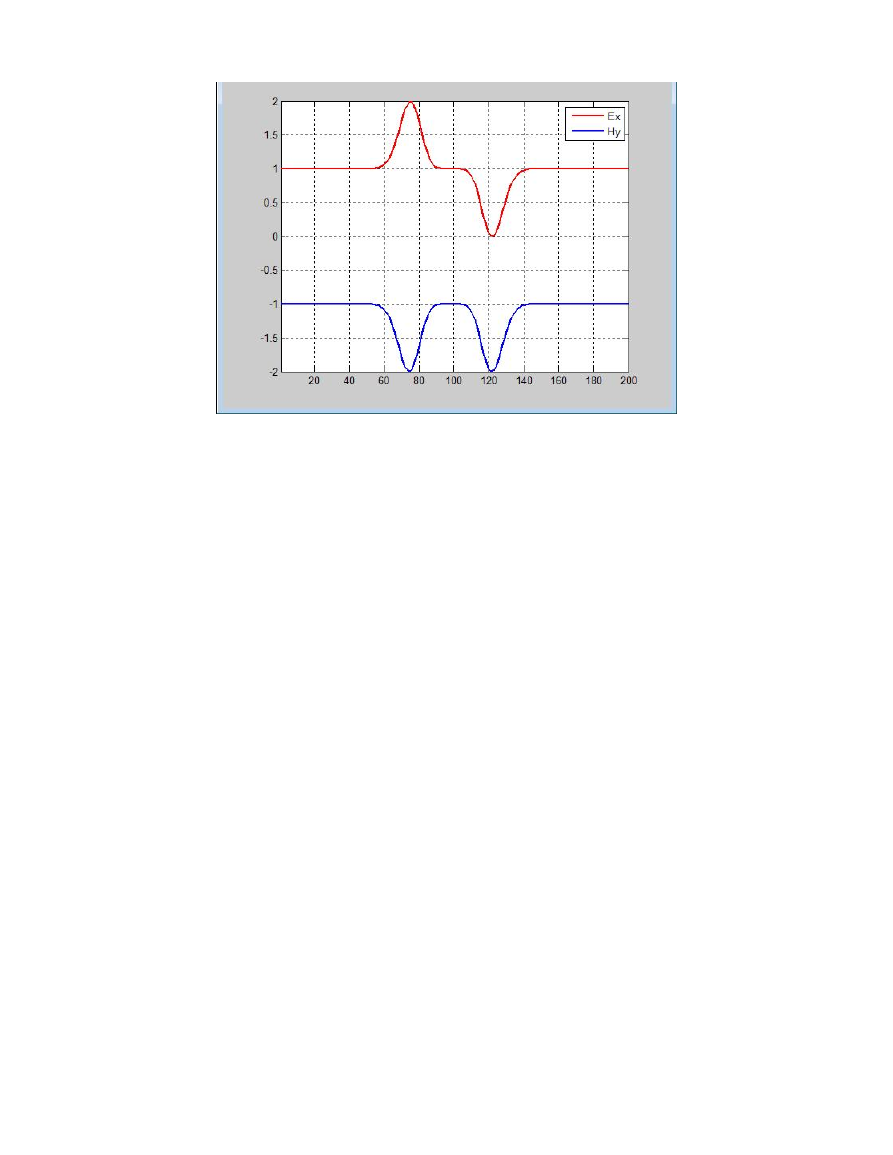
(4) 在程序中，左端添加PEC边界条件，右端添加PMC边界条件，运行程序，给出电磁波经过边界之前、之间、之后的波形图，并尝试观察反射波到达源点位置波形变化图； (30分）答：（左端PEC即令E(2)=0，右端PMC即令H（numCells-1）=0）电磁波经过边界之前的波形图：电磁波经过边界之间的波形图：

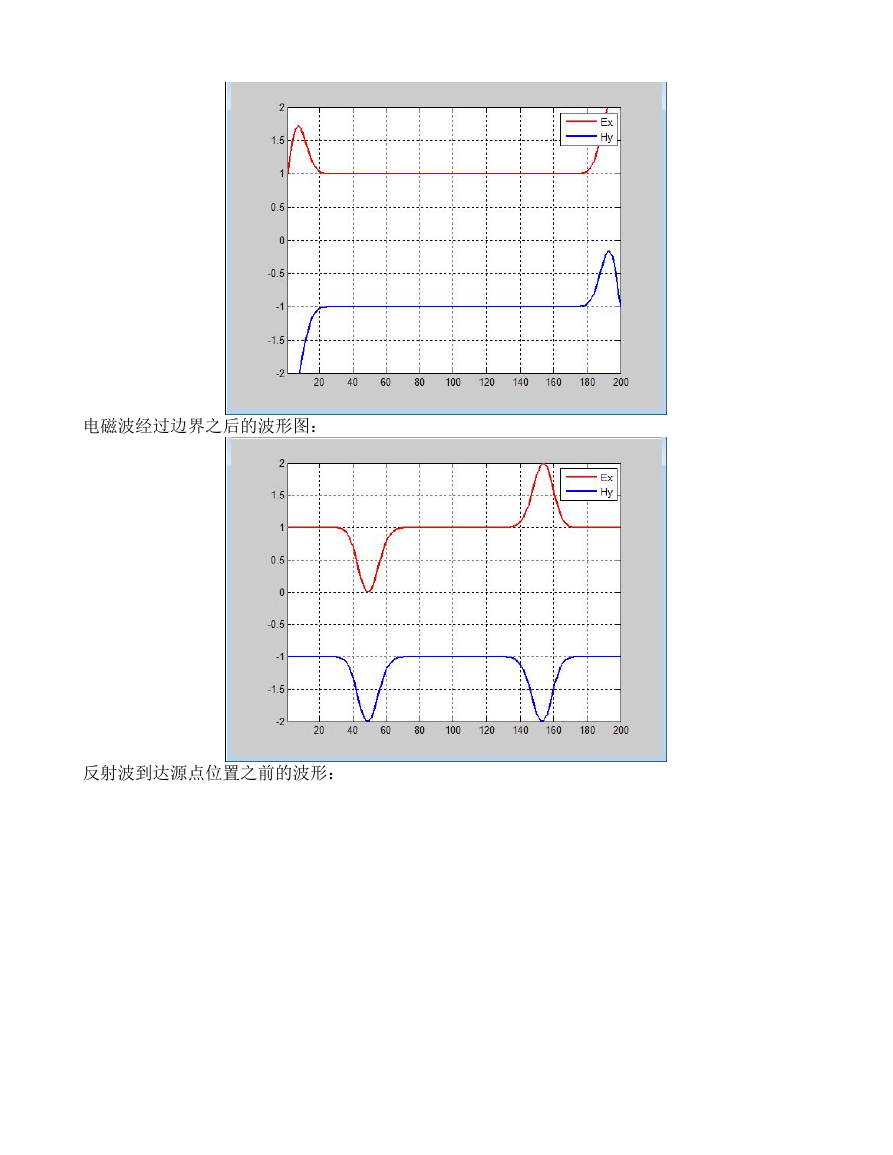
电磁波经过边界之后的波形图：反射波到达源点位置之前的波形：

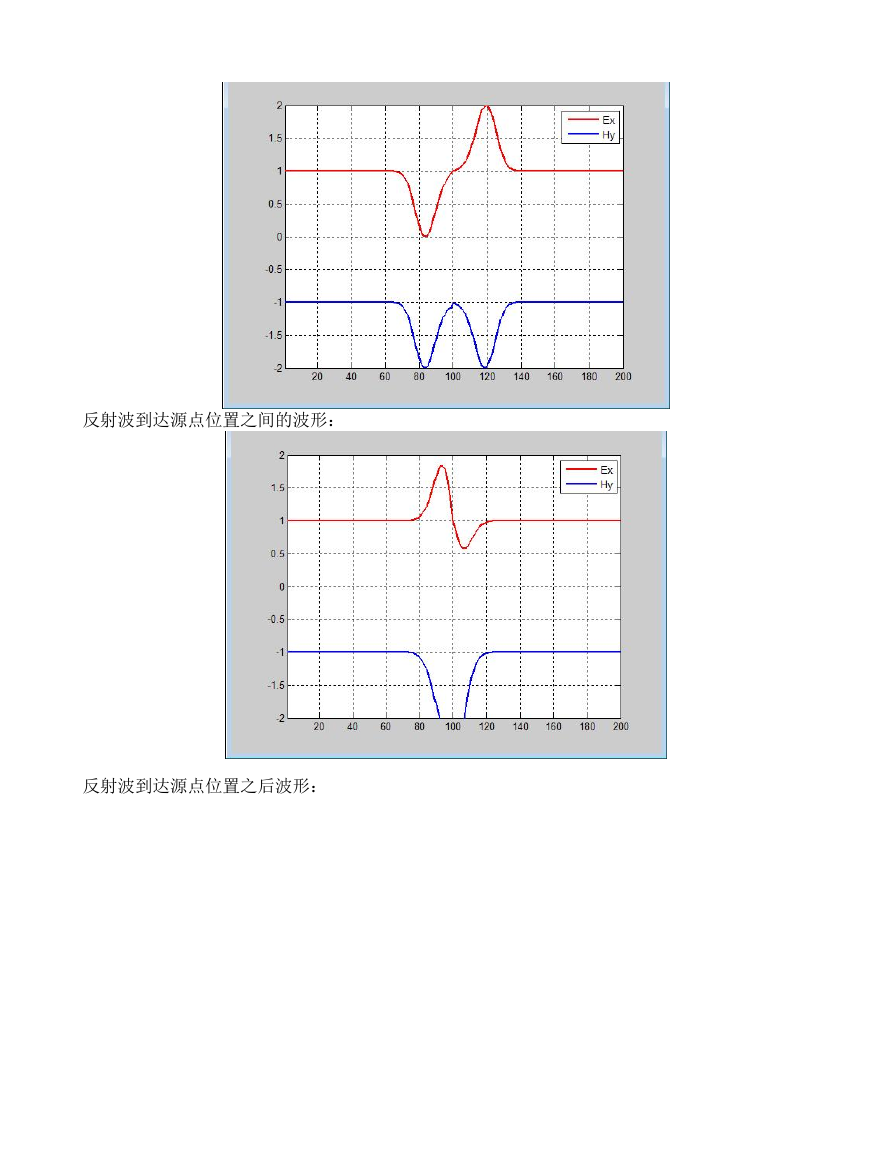
反射波到达源点位置之间的波形：反射波到达源点位置之后波形：

分享到：

赞收藏

资料库

1D_YEE_FDTD_MATLAB.doc

相关推荐

课程资源

热门标签

最新资料