第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
图像处理亚像素.pdf
第35 卷第5 期 光电工程 Vol.35, No.5
2008 年 5 月 Opto-Electronic Engineering May, 2008
文章编号：1003-501X(2008)05-0108-06
基于互相关的图像匹配亚像素定位
雷 鸣，张广军
( 北京航空航天大学 精密光机电一体化技术教育部重点实验室，北京 100083 )
摘要：本文提出了一种新颖的基于抛物线拟合原理的亚像素求取算法。为了简单快速的获得亚像素定位精度，本
文根据相关峰所呈现出的特性，用抛物线拟合经相关峰顶点切开的纵切面轮廓。沿不同的方向纵切，就可获得不
同方向上的拟合抛物线，而根据每一条拟合抛物线可获得其对应顶点。最后根据所获得的点，进一步求取到各点
距离之和的最小值点，其对应位置即为所求。从而实现了以点来描述线（每个点代表一条抛物线），以线（所有的
拟合抛物线）来描述面的思想，以便于更真实详细的描述相关峰顶点附近峰面所呈现出来的特性。实验证明，该
算法具有较高的亚像素提取精度，能达到 0.01 级别的像素精度。
关键词：抛物线拟合；归一化积相关；亚像素；相关峰；费马点
中图分类号：TN911.73 文献标志码：A
Image Orientation Algorithm with Subpixel Accuracy
Based on Correlative Matching Method
LEI Ming，ZHANG Guang-jun
( Key Laboratory of Precision Opto-mechatronics Techonology, Ministry of Education, Beijing
University of Aeronautics and Astronatics, Beijing 100083, China )
Abstract: A new sub-pixel algorithm based on the principle of the parabola fitting is proposed. According to the
condition of the correlation peak, the outline of the longitudinal section along the climax of the correlation peak is fitted
by parabola. The longitudinal section is executed along different direction to acquire different parabola, and then the
climax of parabola can be gained from every parabola. The optimum position is the point, where the sum of distance is the
least from it to all other points. Thus, it is realized that the line of parabola is described by point and the surface of
correlation peak is described by line, which can show more truly the condition of the correlation peak. The experimental
results show that the algorithm maintains a high precision of the subpixel extraction.
Key words: parabola fitting; normalized product correlation; sub-pixel; correlation peak; Fermat point
1 引 言
图像特征的精确定位在许多领域有着极为重要的应用[1]。一些经典的检测算子，如 LOG 算子、Sobel 算
子、Canny[2] 算子等，可对图像特征完成像素级精度的边缘定位，且形式简单，易于实现，速度快。但定
位精度差，而在许多场合中，当提高 CCD 分辨率与光学镜头分辨率受到局限。此时要提高视觉检测系统
的精度，显然，通过改变软件算法比改变系统硬件简单而且有效。因而亚像素目标识别、定位方法将是提
高图像特征定位精度的有效手段。
从 20 世纪 70 年代起就有不少专家提出了一些有效的亚像素边缘定位的方法，如插值法[3]、灰度矩法[4]
和一些组合的算法[5]等，虽然定位精度高，但运行速度很慢，难以得到应用。目前，针对亚像素定位技术
收稿日期：2007-08-18；收到修改稿日期：2008-03-27
基金项目：武器装备预研重点基金资助(6140517)
作者简介：雷 鸣(1976-)，男(汉族)，山东莱州人，博士生，主要从事图像处理，图像匹配的研究。E-mail: lmeagle01@163.com
2008 年 5 月 雷 鸣 等：基于互相关的图像匹配亚像素定位
109
的研究大多集中于曲面拟合法[6]与梯度法[7-8]。而针对基于相关匹配的亚像素定位方法则研究较少。主要是
因为相关匹配具有实现速度慢，运算量大的缺点。但随着专用集成电路与超大规模集成电路技术的发展，
硬件处理速度不断提高，相关匹配定位算法速度慢的缺点已逐渐被克服[9]，而其运算简单、精度高，具有
强适应性及强抗干扰能力的优点则不断被体现。在此背景下，本文针对标准互相关函数对图像进行匹配时，
所形成的峰值点附近的特征，吸取文献[10]提取亚像素边缘的思想，给出了一种新的亚像素定位方法。实
验结果表明，该方法具有精度高，运算速度快的特点。
2 灰度互相关算法原理
相关的基本原理是基于互相关函数的相关特性，用互相关函数来描述评价多幅图像之间的相似程度。
而由相关函数衍生的图像相似程度评测算子有很多：相关算子(CO , Correlation Operator)、标准化互相关算
子(NCCO, Normalized Cross Correlation Operator)、统计相关算子(SCO, Statistical Correlation Operator ) [11]、
相位相关算子(PCO , Phase Correlation Operator) [11]、协方差相关算子(CCO, Covariance Correlation Operator)
[12]等。NCCO 虽然计算量较大，但仍被认为是其中最佳的相似性判据[11]。
如果将标准化互相关算法的准则定义如下：设基准图为 Gr，其大小为 Mr×Nr，实时图为 Gs，其大小为
Ms×Ns，且 Ms
110
光电工程 第 35 卷第 5 期
利用抛物线获得插值点设为(nx，ny)，若设
,(H
yx
)
=
r
xx
r
xy
r
xy
r
yy
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
(2)
其中:
t
=
2
nr
xx
x
nr
x
2
+
+
nr
y
x
nnr
x
xy
y
(
pp
x
,
y
)
=
tn
(
,
tn
( , )
pp
x
,
y
)
y
x
⎡−∈
⎢⎣
1
2
1,
2
⎤
⎡−×⎥⎦
⎢⎣
1
2
1,
2
⎤
⎥⎦
(3)
y
+
2
nr
yy
y
。则该点的亚像素坐标(x0，y0)为
(4)
通过利用抛物线插值的方法，该算法的亚像素提取能达到 0.1 级的像素精度。因为该方法简单易行，
+=
+=
,
tn
tn
y
y
x
x
0
0
y
x
且提取精度高，所以本文将该思想引入到基于相关的亚像素匹配定位上。
4 基于相关的亚像素定位算法
在基于相关的亚像素定位中，一般常用的方法是将相关峰附近看为一个理想的半径为 w，幅度为 h，
中心坐标为 u =u0，v =v0 的高斯曲面，这显然是不够严谨的，通常实际情况无法满足这一要求。另外一种
方法是采用抛物面插值方法。显然这种方法较高斯曲面插值方法更合理，但仍然不够充分。下面对应用情
况进行分析：
一般的抛物面插值法原理是：因为相关峰附近通常不具有圆对称性，因此采用抛物面插值的方法将极
大值附近的曲面视为下抛物面。这种方法显然较高斯曲面插值方法描述更为合理，能够获得更好的结果。
但是也存在两个问题：1) 相关函数极大值附近不一定会是一个理想的下抛物面；2) 所获得的结果精度仅
能达到 0.1 亚像素级别。
−
)
=
在此给出了一种新的插值方法，由相关峰顶点作 8 个方向上(垂直、水平、左斜向和右斜向)的纵切(纵
切数为 4)，显然切面可以用抛物线拟合的方法得到精确描述，从而将文献[10]抛物线插值的方法引入到基
于相关的亚像素定位中来，用二维信息来描述三维信息，获得 4 对 0.1 像素级别的点对：(x1，y1)，(x2，y2)，
(x3，y3)，(x4，y4)，设点(x，y)为到各点距离之和的最小值点。则此点为费马点。
x
(
(5)
yxf
,(
y
()
2
yx 即为所求。而且还可以大大提高插值精度，使之达到 0.01 亚像素级别。
,(
x
(
−
f 处的 )
上式中对应 min
下面针对该方法进行具体说明，假如拟合抛物线是竖直方向的，则有沿竖直方向，利用抛物线插值方
可分别求得
法来拟合，从而获取该处最大的相关系数，然后根据此值代入拟合抛物线方程
其对应的横坐标和纵坐标值。拟合抛物线方程的系数 a、b、c 可由匹配位置处相关峰峰值点附近相邻的 3
个坐标值来确定。设匹配位置处的相关系数为 0ρ ，其横坐标为 0x ，则满足下列等式
0x ,
(
，取
()
2
()
2
()
2
0ρ
bx
ax
bx
ax
y
1
x
1
+
+
=
+
+
=
−
−
+
−
−
+
−
−
(
x
(
x
2
)
2
)
2
)
2
)
+
x
3
x
2
y
3
x
4
y
2
y
4
2
0
c
0
y
2
c
0ρ )附近的其他 2 点( 1x ,
2x ,
1ρ )(
2
ax
=
ρ
0
0
2ρ )，则解如下方程组：
bx
+
+
+
+
=
c
,
2
ax
1
bx
1
ρ
1
0
y
y
y
c
,
ρ
2
=
2
ax
2
+
bx
2
+
c
(5)
从而确定拟合抛物线方程的系数 a、b、c。而真正的实际匹配位置应为相关系数最大处，即为抛物线
方程对应的最高点 Wmax，也就是抛物线的一阶导数等于 0 对应点的坐标，从而可确定沿抛物线方向插值所
对应的横坐标。如上图 2 所示。
同理，可利用纵坐标来确定沿抛物线方向插值所对应的纵坐标值，即
0ρ
2
=
dy
0
+
ey
0
+
f
。最终可获得
所求的坐标值(x1，y1)。
当对水平方向和两个对角线方向进行拟合的时候，参照上面所述，可获得其他对应三点的坐标值(x2，
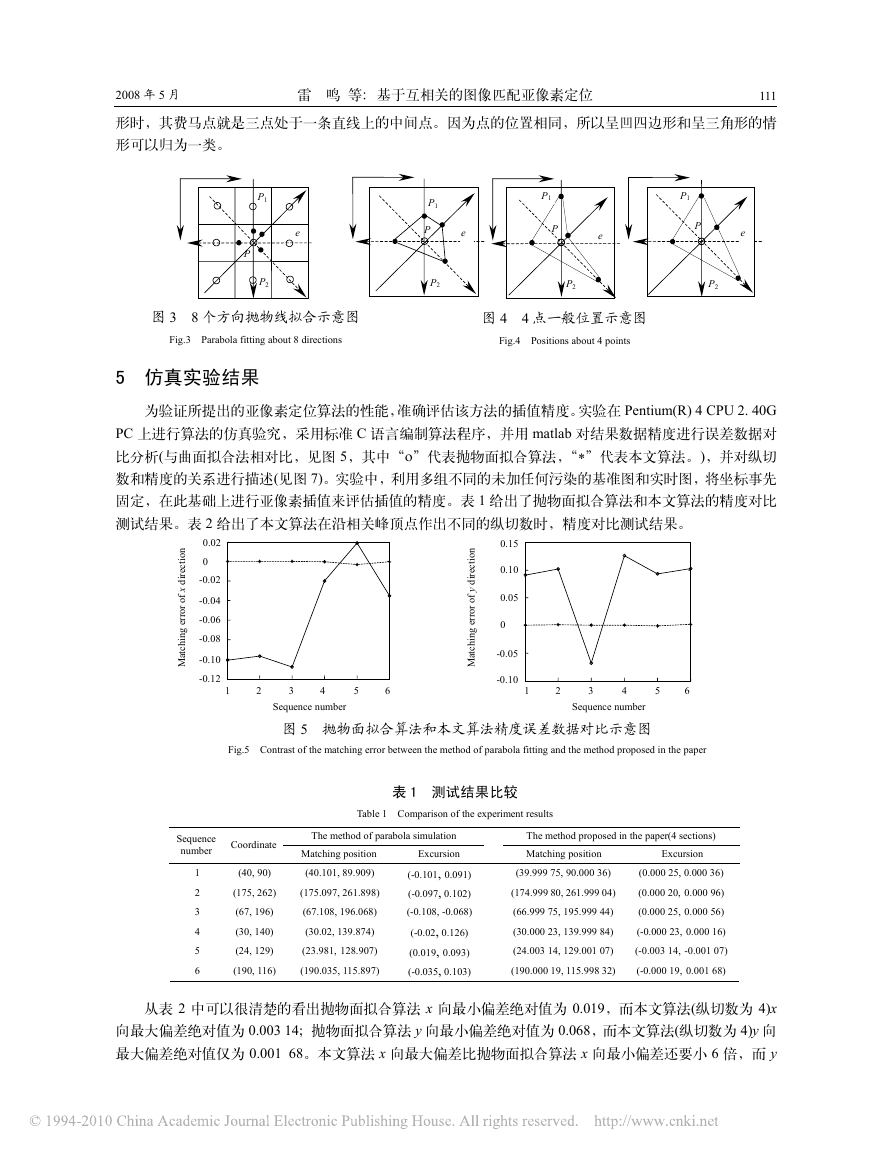
y2)，(x3，y3)，(x4，y4)。8 个方向利用抛物线拟合的示意图如图 3 所示。
而四个点所形成的一般形式分为三种：凸四边形、凹四边形和三角形，如图 4 所示。
利用三角形两边之和大于第三边的初等数学知识，可以很容易证明，四点呈凸四边形时，显然其费马
点(距离各顶点距离和最小的点)就是对角线的交点；呈凹四边形时，费马点就是凹进去的那一点；呈三角
2008 年 5 月 雷 鸣 等：基于互相关的图像匹配亚像素定位
111
形时，其费马点就是三点处于一条直线上的中间点。因为点的位置相同，所以呈凹四边形和呈三角形的情
形可以归为一类。
P1
P
P2
e
e
P1
P
P2
P1
P
e
P1
P
e
P2
P2
图 3 8 个方向抛物线拟合示意图
Fig.3 Parabola fitting about 8 directions
图 4 4 点一般位置示意图
Fig.4 Positions about 4 points
5 仿真实验结果
为验证所提出的亚像素定位算法的性能，准确评估该方法的插值精度。实验在 Pentium(R) 4 CPU 2. 40G
PC 上进行算法的仿真验究，采用标准 C 语言编制算法程序，并用 matlab 对结果数据精度进行误差数据对
比分析(与曲面拟合法相对比，见图 5，其中“ο”代表抛物面拟合算法，“∗”代表本文算法。)，并对纵切
数和精度的关系进行描述(见图 7)。实验中，利用多组不同的未加任何污染的基准图和实时图，将坐标事先
固定，在此基础上进行亚像素插值来评估插值的精度。表 1 给出了抛物面拟合算法和本文算法的精度对比
测试结果。表 2 给出了本文算法在沿相关峰顶点作出不同的纵切数时，精度对比测试结果。
n
o
i
t
c
e
r
i
d
x
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
0.02
0
-0.02
-0.04
-0.06
-0.08
-0.10
-0.12
1
2
3
5
Sequence number
n
o
i
t
c
e
r
i
d
y
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
0.15
0.10
0.05
0
-0.05
-0.10
6
1
2
3
4
5
6
4
Sequence number
图 5 抛物面拟合算法和本文算法精度误差数据对比示意图
Fig.5 Contrast of the matching error between the method of parabola fitting and the method proposed in the paper
表 1 测试结果比较
Table 1 Comparison of the experiment results
Sequence
number
Coordinate
1
2
3
4
5
6
(40, 90)
(175, 262)
(67, 196)
(30, 140)
(24, 129)
(190, 116)
The method of parabola simulation
Excursion
(-0.101, 0.091)
(-0.097, 0.102)
(-0.108, -0.068)
(-0.02, 0.126)
(0.019, 0.093)
(-0.035, 0.103)
Matching position
(40.101, 89.909)
(175.097, 261.898)
(67.108, 196.068)
(30.02, 139.874)
(23.981, 128.907)
(190.035, 115.897)
The method proposed in the paper(4 sections)
Matching position
Excursion
(39.999 75, 90.000 36)
(174.999 80, 261.999 04)
(66.999 75, 195.999 44)
(30.000 23, 139.999 84)
(24.003 14, 129.001 07)
(190.000 19, 115.998 32)
(0.000 25, 0.000 36)
(0.000 20, 0.000 96)
(0.000 25, 0.000 56)
(-0.000 23, 0.000 16)
(-0.003 14, -0.001 07)
(-0.000 19, 0.001 68)
从表 2 中可以很清楚的看出抛物面拟合算法 x 向最小偏差绝对值为 0.019，而本文算法(纵切数为 4)x
向最大偏差绝对值为 0.003 14；抛物面拟合算法 y 向最小偏差绝对值为 0.068，而本文算法(纵切数为 4)y 向
最大偏差绝对值仅为 0.001 68。本文算法 x 向最大偏差比抛物面拟合算法 x 向最小偏差还要小 6 倍，而 y
112
光电工程 第 35 卷第 5 期
向更是达到了 40 倍。显然，本文算法比抛物面拟合算法精度提高了至少一个数量级。图 6 给出了两者的对
比示意图。
表 2 测试结果比较
Table 2 Comparison of the experiment results
The method proposed in the paper(different sections)
Sequence
number
Coordinate
1 point
Matching position
Excursion
1
2
3
4
5
6
(40, 90)
(175, 262)
(67, 196)
(30, 140)
(24, 129)
(190, 116)
(40.000 43, 90.000 43)
(174.999 17, 261.999 17)
(66.999 35, 195.999 35)
(29.999 80, 139.999 80)
(24.018 03, 129.018 03)
(190.001 66, 116.001 66)
(-0.000 43, -0.000 43)
(0.000 83, 0.000 83)
(0.000 65, 0.000 65)
(0.000 2, 0.000 2)
(-0.018 03, -0.018 03)
(-0.001 66, -0.001 66)
2 points
Matching position
(0.001 73, 0.000 89)
(0.002 53, 0.001 5)
(-0.001 15, 0.000 14)
(-0.000 89, 0.001 31)
(-0.001 10, -0.005 39)
(-0.000 47, 0.000 62)
Excursion
(39.999 58, 89.999 43)
(174.999 17, 261.999 17)
(67, 195.999 72)
(30.000 30, 139.999 41)
(24.002 36, 129.009 36)
(190.000 93, 116)
Sequence
number
1
2
3
4
5
6
Coordinate
(40, 90)
(175, 262)
(67, 196)
(30, 140)
(24, 129)
(190, 116)
3point
4 points
Matching position
(39.999 58, 89.999 43)
(174.999 17, 261.999 17)
(67, 195.999 72)
(30.000 30, 139.999 41)
(24.002 36, 129.009 36)
(190.000 93, 116)
Excursion
(0.000 42, 0.000 57)
(0.000 83, 0.000 83)
(0, 0.000 28)
(-0.000 30, 0.000 59)
(-0.002 36, -0.009 36)
(-0.000 93, 0)
Matching position
(39.999 75, 90.000 36)
(174.999 80, 261.999 04)
(66.999 75, 195.999 44)
(30.000 23, 139.999 84)
(24.003 14, 129.001 07)
(190.000 19, 115.998 32)
Excursion
(0.000 25, 0.000 36)
(0.000 20, 0.000 96)
(0.000 25, 0.000 56)
(-0.000 23, 0.000 16)
(-0.003 14, -0.001 07)
(-0.000 19, 0.001 68)
表 2 中，所取一点时，是对应过相关峰顶点 135 度方向上抛物线的最高顶点；2 点时，所取的点是水
平和垂直方向上分别对应的抛物线最高顶点；3 点时，所取的点是水平、垂直和 135 度方向上分别对应的
抛物线最高顶点。随着点数取的越多，其精度也不断增高(参看下面对比示意图 6，其中“ο”代表纵切数
为 1 的情形，“∗”代表纵切数为 2 的情形，“X”代表纵切数为 3 的情形；“+”代表纵切数为 4 的情形)。但是
n
o
i
t
c
e
r
i
d
x
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
5
0
-5
-10
-15
-20
×10-3
1
2
3
4
5
6
Sequence number
n
o
i
t
c
e
r
i
d
y
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
5
0
-5
-10
-15
-20
×10-3
1
2
3
4
5
6
Sequence number
图 6 不同纵切数本文算法精度误差数据对比示意图
Fig.6 Contrast of the matching error about the method proposed in the paper on different sections
×10-3
3.0
2.0
1.0
0
-0.1
n
o
i
t
c
e
r
i
d
x
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
×10-4
n
o
i
t
c
e
r
i
d
y
f
o
r
o
r
r
e
g
n
i
h
c
t
a
M
15
10
5
0
-5
1
2
3
Sequence number
4
1
2
Sequence number
3
4
图 7 纵切数和精度的关系
Fig.7 Diagram of the relation between sections and precision
2008 年 5 月 雷 鸣 等：基于互相关的图像匹配亚像素定位
113
相应的，计算量也越来越大，同时计算复杂度也来越高，取一点时，此点即为所求；2 点时，显然中点为
所求，3 点时，费马点就是所求，4 点时如图 4 分析结果，5 点以上时，计算极其复杂。
从图 7 中可以很清楚的看到，无论是 x 向还是 y 向数据，都是纵切数越多，曲线偏离过零水平直线的
程度越小，即误差越小。下图给出了，随着纵切数的增多，误差减小趋势的曲线图(为清楚显示，仅给出了
4 条曲线)。
从上图中可以看出，虽然有一定的震荡，但是整体基本上仍然是随着纵切数的增多误差呈不断减小的
，这个趋势将更加
趋势。而如果将 x 向偏差和 y 向偏差综合起来一同考虑的话，即考虑
明显(篇幅所限，图表分析略)。
y
(
Δ+
=δ
(
x
Δ
)
2
2
)
6 结 论
本文给出了一种新颖的亚像素求取算法，利用抛物线拟合的原理来描述刻画某一方向被沿顶点纵切开
的相关峰轮廓线，进而获得此方向上的拟合曲线最高顶点。在不同的方向依次纵切，就会得到不同的顶点，
然后根据所获得的点，进一步求取到各点距离之和的最小值点，其对应位置即为所求。实验结果表明，本
文算法具有很高的亚像素精度，且随着纵切数的提高，精度会越来越高，但是计算也会越来越复杂。尤其
是当纵切数大于等于 5 时，如何降低其计算复杂度。这在以后的工作当中有待下一步深入研究并加以解决。
参考文献：
[1] West G A W，Clarke T A. A survey and examination of subpixel measurement techniques [C] // Proceedings of the Meeting，
Close-range Photogrammetry Meets Machine Vision. Bellingham：Society of Photo-optical Instrumentation Engineers，
1990：456-463.
[2] Canny J. A computational approach to edge detection [J]. IEEETransactions on Pattern Analysis and Machine Intelligence，
1986，8(6)：679-698.
[3] LU H，CARY P D. Deformation measurement by digital image correlation：implementation of a second-order displacement
gradient [J]. Experimental Mechanics，2000，40(4)：393-400.
[4] Lyvers E P，Owen R M，Mark L A，et al. Subpixel measurements using a moment-based edge operator [J]. IEEE Transactions
on Pattern Analysis and Machine Intelligence，1989，11(12)：1293-1308.
[5] 叶声华，段发阶，张洪涛. 一种快速亚像素边缘检测方法研究 [J]. 计量学报，2002，23(4)：263-265，270.
YE Sheng-hua，DUAN Fa-jie，ZHANG Hong-tao. Study on a fast method for sub-pixel edge detection [J]. Acta Metrologica
Sinica，2002，23(4)：263-265，270.
[6] Hung P C，Voloshin A S. In-plane Strain Measurement by Digital Image Correlation [J]. J of the Braz Soc of Mech Sci & Eng，
2003，25(3)：215-221.
[7] Zhou P，Goodson K E. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation [J].
Opt Eng，2001，40(8)：1613-1620.
[8] Zhang J，JIN G C. Application of an improved subpixel registration algorithm on digital speckle correlation measurement [J].
Optics & Laser Technology，2003，35：533-542.
[9] Alzahrani F M，CHEN T A. A real-time edge detector：algorithm and VLSI architecture [J]. Real-Time Imaging，1997，3：
363-378.
[10] Carsten Steger. An Unbiased Detector of Curvilinear Structures [J]. IEEE Transactions on Pattern Analysis and Machine
Intelligence，1998，2(20)：113-125.
[11] Brown L G. A survey of image registration techniques [J]. ACM Computer Surveys，1992，24(4)：325-376.
[12] 于起峰，陆宏伟，刘肖琳. 基于图像的精密测量与运动测量 [M] . 北京：科学出版社，2002：148-150.
YU Qi-feng，LU Hong-wei，LIU Xiao-lin. Image based precise measurement and motion measurement [M]. Beijing：
Science Press，2002：148-150.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
