logo资料库

原创细菌群优化算法程序和算法-基于细菌群体趋药性的函数优化方法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.41M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第 10 卷 第 1 期 电路与系统学报 Vol.10 No.1 2005 年 2 月 JOURNAL OF CIRCUITS AND SYSTEMS February， 2005 文章编号：1007-0249 (2005) 01-0058-06 基于细菌群体趋药性的函数优化方法* 李威武 1， 王慧 1， 邹志君 2， 钱积新 1 （1. 浙江大学 控制系系统工程研究所，浙江 杭州 310027；2. 浙江大学 动力机械及车辆工程研究所，浙江 杭州 310027） 摘要：本文在细菌趋药性（Bacterial Chemotaxis，BC）优化算法基础上提出一种基于群体智能的函数优化方法－ 细菌群体趋药性（Bacterial Colony Chemotaxis，BCC）算法。细菌群体趋药性算法同时使用单个细菌在引诱剂环境下 的应激反应动作和细菌群体间的位置信息交互来进行函数优化。细菌群体趋药性算法在保留单个细菌较强的搜索能力 的基础上克服了细菌趋药性算法收敛速度较慢，性能难以与其他常用的智能优化算法比较的不足。对不同函数优化试 例的仿真表明细菌群体趋药性算法性能良好，是一种具有进一步研究价值的集群函数优化方法。 关键词：细菌趋药性；函数优化；群体优化；智能优化；随机优化方法 中图分类号：TP18 文献标识码：A 1 引言 在众多的函数优化算法中，有很多源自于大自然生物过程的启迪，例如生物的进化过程[1]，昆虫 的觅食行为[2]。这些基于群体智能的优化方法对于解决很多多峰、非连通、甚至难以建立数学模型的 优化问题有着很好的效果，并在很多实际问题如调度、设计、控制等问题上走向应用。 基于细菌趋药性（Bacterial Chemotaxis，BC）的函数优化方法[3]是一种新的从生物行为中获得灵 感的优化方法。这种优化方法旨在利用细菌在化学引诱剂环境中的运动行为来进行函数优化。这项工 作最早由 Bremermann[4]及其同事进行，Muller 在他们的工作上进一步综合提出了细菌趋药性算法。BC 算法总体性能上可以与一些基于群体智能的优化算法进行比较，不过效果要差。但是，基于细菌趋药 性的优化算法作为一种新的基于生物行为的优化方法，它的实现思想与传统的群体优化方法如遗传算 法（GA），进化策略（ES）有很大不同。BC 算法不是一种基于群体智能的优化方法，它只依赖于单 个细菌的运动行为，它不断地感受它周围环境的变化并且只利用它过去的经验来寻找最优点。BC 算 法的简单性和鲁棒性表明这是一个值得进一步深入研究的方向。 本文提出一种从细菌趋药性算法发展起来的新的基于群体智能的优化方法：细菌群体趋药性 （Bacterial Colony Chemotaxis，BCC）算法。在 BCC 算法中，假定细菌在引诱剂环境中通过一些简单 的假设方式进行通信。细菌不仅使用自己的运动位置信息也利用其他细菌的位置信息进行函数优化。 对不同的评价函数进行的试验表明，细菌群体趋药性优化算法不仅极大地提高了细菌趋药性算法的优 化能力，而且在一些问题上的优化速度和精度也超过了其他一些常见的群体优化算法。 2 BC 算法描述 为了清楚的描述 BC 算法，仅解释二维环境下的情况。多维空间下的 BC 算法实现以及其余的 BC 算法细节可以参考文献[3]。 简单说来，细菌对引诱剂的反应运动遵守如下的假设：1）细菌的运动轨迹是由一系列的直线组成， 并且由速度、方向和持续时间三个参数决定；2）在所有运动轨迹中细菌的运动速度设为恒定；3）细 菌在改变运动方向时，向左拐和向右拐的概率相同；4）细菌在各段运动轨迹上的移动时间和各段相邻 轨迹间的夹角都由概率分布来决定。 BC 算法的步骤如下所示： * 收稿日期：2003-06-30 修订日期：2004-12-05 基金项目：浙江省自然科学基金资助项目（601119）
    第 1 期 李威武等：基于细菌群体趋药性的函数优化方法 59 1）计算细菌的移动速度 v，假定其为常数 1： 2）计算细菌在新方向上的移动时间τ。τ的数值由概率分布决定： 1=v （1） （2） XP ( ) τ / τ − = = e T 1 T 参数 T 由下式决定： f l , for pr 1 + b ⎛ ⎜ ⎜ ⎝ f l pr pr for ⎞ ⎟ , ⎟ ⎠ T = ⎧ T ⎪ 0 ⎪ ⎨ ⎪ T ⎪ 0 ⎩ >= 0 < 0 （3） 其中 0T 为最小平均移动时间， prf 为当前点和上一个点的 函数值的差， prl 为变量空间中连接当前点和上一个点的向 量的模， b 为与维数无关的参数。 3）计算新运动方向。新方向与原来轨迹的夹角根据新 方向向左或向右偏转分别服从下面两个高斯概率分布： pr f l pr pr µναXP ( ) = = , = 1 2 πσ exp − ⎡ ⎢ ⎣ 2 ( ) − να 2 2 σ ⎤ ⎥ ⎦ （4-a） µναXP ( ) −= = , = 1 2 πσ exp − ⎡ ⎢ ⎣ 2 ( ) − να 2 2 σ ⎤ ⎥ ⎦ （4-b） 其中，它们的期望 (XE=µ ) 和方差 =σ Var (X ) 分别按如下的方式给定：如果 f l pr pr 0< ， µ = 62o 1( − cos( )) θ （5） σ = 1(26o − cos( )) θ （6） cos( θ −=) ce ττ pr （7） 其中 cτ 为相关时间， prτ 为细菌上一运动轨线的持续时间；如果 4）计算细菌在变量空间中新的位置： r x new = pr f l r x old pr 0> ， o62=µ ， o26=σ 。 + r ln u （8） 其中， newxr 为细菌新位置， oldxr 为细菌上一时刻的位置， unr 是正则化的新轨线的方向向量， l 为新轨线 的长度。整个算法中， 0T 、 cτ 、b 为三个需要设定的系统参数。 BC 算法给出了确定系统参数 0T 、 cτ 、b 的一种方式[3]，它们与期望的计算精度ε相关。 = εT 0 30.0 ⋅ 10− 73.1 （9） Tb 0 = ⋅ 54.1 −T ( 0 60.0 ⋅ 10 ) （10） cτ = ⎛ ⎜⎜ ⎝ b T 0 ⎞ ⎟⎟ ⎠ 31.0 16.1 10⋅ （11） 在优化过程中对算法参数的自适应调整可加速寻优过程。文献[3]提供了多种参数更新的方法，本 文只介绍 BCC 算法中沿用的全体参数更新策略。在搜索过程中对全体参数进行自适应更新的方法是： a）设定搜索过程中的初始精度 beginε 和最终精度和 endε 。利用式（9）~（11）和 beginε 确定参数 0T 、 cτ 、b。 beginε 一般可取大于 0.1 的一个值， endε 则可以取一足够小的值如 10-10； b）定义参数进化的代数 iterN ，一般可以设定为 100~500。每次达到某一搜索精度后，就进入下一 精度范围，同时根据式（9）~（11）重新确定参数 0T 、 cτ 、b； c）当连续 pcn 步前后函数值的差的绝对值小于ε时，即 采用全体参数的自适应更新后，细菌在搜索初期当初始精度较低时，移动的步长较大，可以避免 ，则此时给定的精度ε已经达到。 ε
    60 电路与系统学报 第 10 卷 的增加，BC 算法很难保证将其搜索范围限定在最优值范围附近。 现实世界中，没有生物是完全独立地生活的。尽管细菌是很细微的生物，它们也必定通过某种方 式相互联系，很多研究表明某些细菌群体在觅食过程中也有群聚现象[5]，细菌之间通过各种方式交换 食物信息。使用同伴提供的信息，细菌将能够大大扩展他们对于环境的了解从而能增加存活的几率。 在一个放置有引诱剂的环境中，假定细菌群体间遵照以下的方式进行相互联系： 1）现实情景中，一种已被人们理解的菌类聚群的方式是通过释放对其它细菌起引诱剂作用的化学 物质来进行联系[5]，也可能存在很多尚未为人所知的其它方式。可以假定每一个细菌都有一定的感知 范围（ SenseLimit ），在这个范围内细菌可以感知其它细菌以及它们的状态； 2）假定每个细菌都有一定的智能可根据它感知范围内其它细菌的信息来调整移动的方式。根据 Reynolds 对于生物群体分布式行为模式的描述[6]，假定细菌群体在一定条件下也遵守聚群和速度匹配 等模式： a）在每次移动到新位置之前，细菌都要感知它周围的环境，试探旁边是否有其他位置更好的细菌。 如果有，那么它有可能趋向移动到这些拥有较好位置细菌的中心点。在移动步数为 k 时细菌 i 附近有 更好位置的同伴的中心点由下式决定： r xf ( （12） SenseLimit dis AND Center ) < ) < r x r x , ) ) ( ( ( | r x ki , kj , kj , kj , r xf ( ki , r x ki , ) = n ⎛ = ∑ ⎜ ⎝ Aver ⎞ ⎟ ⎠ r x i =1 i 其中， Aver ( r x 1 , r x 2 ,... r x n ) n ， i j , = n ,...2,1 ， dis ( r x , r x ki , ) kj , 为细菌 i 和细菌 j 之间的距离； rand rand 为(0, 2)之间服从均匀分布的随机值； b）如果一个细菌趋向移动到它周围同伴的中心位置，移动的长度为 ) ( c）各细菌在移动的过程中速度保持相同； 3）模拟菌群的迁徙现象。当细菌在某处连续一段时间感触引诱剂信息变化很小时，由于它们总希 望寻觅更好的食物源，往往会进行不同方式的迁徙活动[5]。作为该迁徙活动的一种模拟，当连续 en 步 ε< 时，细菌随机迁徙到一个新位置，并且此前所 前后函数值的差的绝对值小于预先给定的 eε ，即 有位置信息丢失。通过迁徙活动，可帮助细菌群体保持群体的差异性，同时也有助于跳出局部最小点。 4 细菌群体趋药性（BCC）算法 Center dis prf ) ( ， )) , ki , ki , ( ( ⋅ e r x r x 通过上面介绍的细菌趋药性算法和细菌群体在引诱剂环境下的信息交换模式，提出一种新的集群 智能优化算法－细菌群体趋药性（BCC）算法。 即 / αε old ，α为精度更新常数，可取大于 1 的一个值。 为了方便，对 BC 算法中的精度更新方式进行改进，将原先的等差更新方式替换为级数更新方式， ε new = 以寻求函数的最小值的优化过程为例，基本的 BCC 算法步骤如下： 1）初始化各个细菌的位置。根据变量范围，随机将细菌群体分布在不同的位置； 2）确定初始收敛精度 beginε 和进化精度更新常数α； 3）采用式（9）~（11）确定算法参数。本文中假定每个细菌都有全局的感知范围； 4）对处在移动步数 k 的细菌 i，感知其周围有更好位置的其他细菌，并确定它们的中心点 ) Center r ,kix ( 和一个假定的朝这个中心方向移动的长度 rand ) ( ⋅ dis ( r x , Center ( r x )) ki , ki , ，确定位置 ' , +kixr ； 1 5）对处在移动步数 k 的细菌 i，同时根据它自己记忆的上几步的位置信息按 BC 算法确定在步数 k+1 时的新位置 '' 6）计算位置 ' , +kixr ； 1 , +kixr 和位置 '' 否则就移向点 '' 1 , +kixr ； 1 , +kixr 的函数值，如果 1 r xf ' ( ki , ) + < 1 r xf '' ( ki , 1 + ) , 那么细菌就在 k+1 步移向点 ' , +kixr ， 1 7）重复步骤 3）~6），直至中止条件满足。一般在运行几百次后可以结束迭代。 在步骤 3）~6）中，同时采用全体参数更新策略进行参数更新和细菌的迁徙动作。 由于 BCC 算法是一种随机优化算法，为了进一步提高算法性能，避免由于算法的随机性而将原来
    第 1 期 李威武等：基于细菌群体趋药性的函数优化方法 61 位置较好的点抛弃的情况，引入精英保留策略。即菌群每移动一步后，位置最差的细菌将继续移动到 菌群整体移动前位置最好的细菌所处的位置附近， ， rand 在(0, 2)间服从均匀分布。 rand ) ( ) ( − + = r x r x r x ⋅ ( r x best ) worst worst worst 利用单个细菌移动轨迹的信息和感知到的周围同伴的位置信息，BCC 算法具有 BC 算法易于从局 部极值逃脱的优点，也拥有群体优化算 法的强大的空间搜索能力。与 BC 算法 相比较，BCC 算法能够更快的搜索到极 值点，因为 BCC 算法中细菌通过与周围 同伴交换信息可以大大节省在解空间中 搜索的时间。同时 BCC 算法中，由于细 菌群体间的相互作用，细菌群体的大部 分都不易从最后的全局最小点逃逸，而 这是 BC 算法难以解决的问题。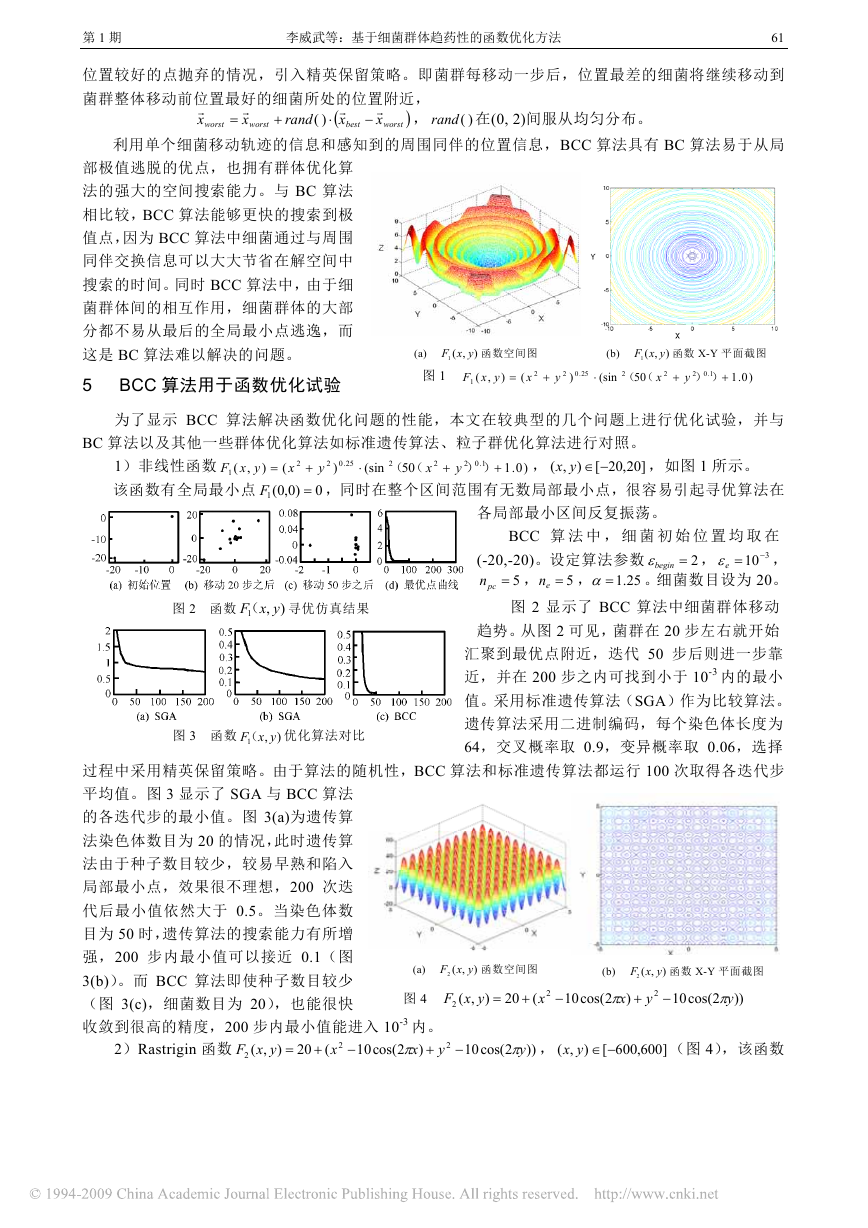 5 BCC 算法用于函数优化试验 yxF ,(1 (a) 图 1 yxF ,(1 x 50 2 （（ 2 ) 函数空间图 (b) ) 函数 X-Y 平面截图 yxF 1 ( , ) = 2 ( x + 2 y ) 25.0 ⋅ (sin + y 1.0 2 + ）） )0.1 为了显示 BCC 算法解决函数优化问题的性能，本文在较典型的几个问题上进行优化试验，并与 BC 算法以及其他一些群体优化算法如标准遗传算法、粒子群优化算法进行对照。 ]20,20 −∈yx ,( [ 2 （（ ， 25.0 ) 2 2 1）非线性函数 x yxF , ) = 1 F )0,0(1 该函数有全局最小点 ( ( + = y 0 ⋅ (sin ) ，同时在整个区间范围有无数局部最小点，很容易引起寻优算法在 ，如图 1 所示。 1.02 + ）） )0.1 50 + y x 2 各局部最小区间反复振荡。 , ) , ) ， ， 2= 310− =eε ， 5=en 图 3 函数 图 2 函数 yxF（ 优化算法对比 1 yxF（ 寻优仿真结果 1 (-20,-20)。设定算法参数 5=pcn 25.1=α BCC 算 法 中 ， 细 菌 初 始 位 置 均 取 在 ， beginε 。细菌数目设为 20。 图 2 显示了 BCC 算法中细菌群体移动 趋势。从图 2 可见，菌群在 20 步左右就开始 汇聚到最优点附近，迭代 50 步后则进一步靠 近，并在 200 步之内可找到小于 10-3 内的最小 值。采用标准遗传算法（SGA）作为比较算法。 遗传算法采用二进制编码，每个染色体长度为 64，交叉概率取 0.9，变异概率取 0.06，选择 过程中采用精英保留策略。由于算法的随机性，BCC 算法和标准遗传算法都运行 100 次取得各迭代步 平均值。图 3 显示了 SGA 与 BCC 算法 的各迭代步的最小值。图 3(a)为遗传算 法染色体数目为 20 的情况，此时遗传算 法由于种子数目较少，较易早熟和陷入 局部最小点，效果很不理想，200 次迭 代后最小值依然大于 0.5。当染色体数 目为 50 时，遗传算法的搜索能力有所增 强，200 步内最小值可以接近 0.1（图 3(b)）。而 BCC 算法即使种子数目较少 图 4 （图 3(c)，细菌数目为 20），也能很快 收敛到很高的精度，200 步内最小值能进入 10-3 内。 y 2 函数 X-Y 平面截图 10 2）Rastrigin 函数 （图 4），该函数 yxF ,(2 yxF ,( 2 yxF ,(2 y 2 + (b) x )2 π −∈yx ,( [ 600,600 函数空间图 x )2 π cos( cos( cos( cos( y 2 π y 2 π (a) 10 10 20 10 20 ， ( x ( x )) )) − ) = − + 2 − − + + ) ] ) ) 2 yxF ,( 2 ) =
    62 电路与系统学报 第 10 卷 0) =yxF ,(2 有全局最小点 BCC 算法与 SGA 算法的初始种子都在 ，同时在区间范围内有大量的局部最小点。 中随 机选取，两种算法都运行 100 次取得平均值。BCC 和 SGA 的参 数设定均与上例相同，细菌数目设为 20（图 5(b)），染色体数目 设为 100（图 5(a)）。 yxF ,(2 对于实验函数 −∈yx ,( [ ,600 600 ) ] ) 图 5 函数 yxF ,(2 ) 优化算法对照 ) yxF ,(2 对于试验函数 ，SGA 的表现不很理想。100 次试验中， 很多次无法逃离局部最小点，从而影响了最后的优化效果。BCC 算法似乎能够较好逃离局部最值，数 目为 20 的菌群能在 300 步之内找到小于 10-6 的最小值。 ，还采用 BCC 算法与其他优 化算法在指定最大搜索步长时进行性能比较。这些优化 算 法 分 别 是 进 化 策 略 （ ES ） 方 法 、 CMA 进 化 策 略 （CMA-ES）、纯随机搜索（PRS）方法、BC 算法。每 种优化方法都运算进行 30 次获得平均值。ES、CMA、 BCC 种子个数均为 10。除 BCC 外，这些算法的设置和 结果均来自文献[3]。表 1 显示了这些优化方法的结果。 可见，对 Rastrigin 函数 BCC 显示了很好的寻优能 表 1 各算法用于 yxF ) cos( ,( 20 ( = + 2 y y 10 2 cos( 2 + − π 最大迭代步长 寻优精度 成功率 方法 CMA-ES 33% 37% 0.1% 10% 100% − 优化的性能比较 50000 50000 50000 50000 500 0.9 0.9 0.9 0.9 10-6 ES PRS BC BCC x )2 π x )) 10 2 力，能在较少的迭代步数内达到较高的精度范围。同时，BCC 算法的成功率也很高。 3）Schaffer’s f6 函数 yxF ,( 3 ) = 2 x (sin + (001 .01( + 2 y x 2 2 ) + − y 2 5.0 2 )) − 5.0 ， −∈yx ,( [ ) ]100 ,100 。Schaffer’s f6 函数具有 一个全局最小点 −=（F )0,03 1 。在全局最小点周围，无限多的局部最小点将全局最小点（其函数值约为 0.9903）包围，如图 6 所示。Schaffer’s f6 函数的强烈振荡性质和全局最小点 被无数多局部最小点环绕的特性使得 它的优化十分困难。一般算法难以得 到最优解[7]，是 GA-难度非常大的问 题[8]。 (a) Schaffer’s f6 函数空间图 (b) Schaffer’s f6 函数 X-Y 平面截图 对于函数 Schaffer’s f6 的优化， 本文采用粒子群优化（PSO）算法作 为参照算法。PSO 算法是集群智能的 代表性方法之一，自 1995 年提出以 来，在函数优化等方向的应用研究非常活跃[9,10]。对照实验中 PSO 算法的设置参照文献[13]（文献中 的最大值），粒子数为 30，最大允许进化代数为 10000，当误差小于 10-5 时进化停止。随 是求 机运行 20 次，然后统计 20 次实验的平均进化代数。BCC 算法的参数设置如前两例，细菌数目设为 20。 BCC 算法试验的收敛原则与 PSO 算法相同。结果如表 2 所示，其中标有“*”的数据来自文献[11]。 图 6 Schaffer’s f6 函数 yxF（− ) , 3 可见，BCC 算法在 Schaffer’s f6 函数的优化上也有很好的表现。 通过以上的函数优化实验，发现 BCC 算法显示出比 BC 算法要好得多的性能，在这几个试验函数 上也优于其他一些群体优化算法如 SGA、ES、PSO。BCC 算法呈现出了种群数目较少、收敛速度快、 精度高的特点。 6 结论 表 2 各算法用于 Schaffer’s f6 函数优化的性能比较 PSO 压缩方法 方法 （最大速度 100000） PSO 压缩方法 （ ） X V = max max PSO 惯性 权重方法 BCC 算法 BCC 算法 由于采用了 寻优过 程中的细菌群体交互模式而大大提 高了细菌的寻优能力，是一种具有潜力的群体智能优化方法。BCC 算法与原始的 BC 算法及其他的群 平均进化代数 512.35* 430.55* 532.4* 308.75
    第 1 期 李威武等：基于细菌群体趋药性的函数优化方法 63 体进化优化算法相比具有以下特点： 1）全局性：各细菌的移动步长按照概率分布取值，因此 BCC 算法具有固有的突破局部最值限制 的性能；同时细菌群体的迁徙活动也有助于细菌群从局部最值逃逸； 2）快速性：与 BC 算法相比，BCC 算法允许细菌采用其他同伴的经验来指导自己的移动路线。 因此 BCC 算法中的细菌不仅能从它自己过去的移动路线中进行学习，也可以利用周围其他菌类的位置 信息，可以更快更准确地模拟环境的梯度信息，从而快速趋近最小值； 3）较高的精度：与其他群体优化算法（GA，ES 等）相比，BCC 具有更强的局部搜索能力。在 几乎所有的其他基于群体的优化中，单个种子在脱离周围群体影响时只能进行完全随机的搜索，而 BCC 算法中的单个种子也有一定的寻优能力，特别是 BCC 算法继承了 BC 算法中的变尺度搜索的优 点，从而具备了获取较高精度极值的良好性质； 4）较低的资源占用：BCC 算法一般选取较少的种子数目就可以达到精度要求。 虽然目前对基于细菌趋药性的优化的研究还不够系统，但对其初步讨论已表明这是一种具有进一 步研究意义的集群函数优化方法，希望它能引起更多智能优化研究人员的注意。 参考文献： [1] Holland J H. Adaptation in Nature and Artificial Systems [M]. MIT Press, 1992. [2] Dorigo Marco, Maniezzo Vittorio, Colorni Alberto. Ant System: Optimization by a Colony of Cooperating Agents [J]. IEEE Transaction on SMC, Part B, 1996, 26(1): 29-41. [3] Muller S D, J. Airaghi Marchetto S, Koumoutsakos P. Optimization Based on Bacterial Chemotaxis [J]. IEEE Transaction of Evolutionary Computation, 2002, 6(1): 16-29. [4] Bremermann H J. Chemotaxis and Optimization [J]. J. Franklin Inst., 1974, 297: 397-404. [5] Passino K M. Biomimicry of bacterial foraging for distributed optimization and control [J]. IEEE Control System Magazine, 2002-06. 52-67. [6] Reynolds C W. Flocks, herd, schools: a distributed behavioral mode [A]. Proceeding of SIGGRAPH’87, Computer Graphics [C]. Anaheim, California. 1987, 21(4): 25-34. [7] 王凌. 智能优化算法及其应用 [M]. 北京: 清华大学出版社, 2001. [8] 李敏强, 寇纪淞, 林丹, 李书全. 遗传算法的基本理论与应用 [M]. 北京: 科学出版社, 2002. [9] [10] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space [J]. IEEE Trans. Kennedy J, et al. Particle Swarm optimization [A]. Proc. IEEE Int. Conf. on Neural Networks [C]. Perth, WA, Australia, 1995. 1942-1948. Evolutionary Computation, 2002, 6(1): 58-73. [11] Eberhart R C, Shi Y. Comparing inertia weights and constriction factors in particle swarm optimization [A]. Proc. 2000 Congress on Evolutionary Computation [C]. Piscataway, NJ: IEEE Service Center, 2000. 84-88. 作者简介：李威武（1976-），男，博士研究生，从事智能优化和智能控制等研究；王慧（1959-），女，教授，从事系 统优化及系统工程理论等研究；邹志君（1978-），女，硕士研究生，从事智能诊断和优化控制等研究；钱积新（1939-）， 男，教授，博士生导师，从事系统优化及智能决策等研究。 Function optimization method based on bacterial colony chemotaxis LI Wei-wu1, WANG Hui1, ZOU Zhi-jun2, QIAN Ji-xin1 ( 1. Institute of Systems Engineering, Zhejiang University, Hangzhou 310027, China; 2. Institute of power mechanical and vehicle engineering, Zhejiang University, Hangzhou 310027, China ) Abstract: We present a new kind of collective intelligent function optimization method, Bacterial Colony Chemotaxis (BCC) algorithm, based on Bacterial Chemotaxis (BC) algorithm. BCC algorithm takes advantage of both a single bacterium’s reaction to chemoattractants and the exchange of position information among bacteria to find the optimum. BCC algorithm much improves the performance of BC algorithm while possessing the searching ability of a single bacterium, making it comparable to many other well-used intelligent optimization methods. The simulation of some test function optimization using BCC algorithm shows BCC algorithm a kind of potentially powerful optimization method worth of much more research. Key words: bacterial chemotaxis; function optimization; collective optimization; intelligent optimization; stochastic optimization methods
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料