下行链路多用户MIMO系统中的MRT预编码.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：1.03M 资料格式：pdf 举报版权申诉

weixin_38520275-15617919-16359647386866017301.pdf-第1页.png

第1页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第2页.png

第2页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第3页.png

第3页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第4页.png

第4页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第5页.png

第5页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第6页.png

第6页 / 共7页

weixin_38520275-15617919-16359647386866017301.pdf-第7页.png

第7页 / 共7页

Abstract

Introduction

System model

MUI as interference

Precoding scheme

BD precoding algorithms

Proposed precoding

Simulation results

Conclusions

Competing interests

Author details

References

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 DOI 10.1186/s13638-016-0738-6 R ES EAR CH MRT precoding in downlink multi-user MIMO systems Yinghui Zhang1, Jing Gao2* and Yang Liu1 Open Access Abstract This paper focuses on the design of maximum ratio transmission (MRT) precoding for multi-user multiple-input multiple-output (MU-MIMO) downlink transmission. Exiting block diagonalization (BD) precoding studies on MU- MIMO systems have the high complexity, because the transmitter precoding matrices constructed by singular value decomposition (SVD) are successively calculated twice. The MRT scheme construct precoding vectors aimed at each received antennas, respectively, so the signals of every antenna are independent. More spatial diversity gain can be obtained compared with BD precoding when MRT precoding and maximum ratio combining are employed. Simulations show that the proposed algorithm has many gains over the conventional BD precoding in various MU-MIMO systems. Keywords: MU-MIMO, Precoding, Multi-user interference, Maximum ratio transmission 1 Introduction The envisioned rapid increase of the wireless data traffic de- mand in the next years imposes rethinking current wireless cellular networks [1]. Multi-user (MU) multiple-input multiple-output (MIMO) systems have the potential of combining the high capacity by MIMO processing with the benefits of space-division multiple access (SDMA) [2]. In general, MU-MIMO systems not only suffer from the noise and the inner-antenna interference but are also affected by multi-user interference (MUI) during downlink transmis- sion, which is means of channel-aware precoding methods implemented at the base station (BS). Precoding techniques for MIMO transmissions have recently gained increasing interest with the introduction of MU-MIMO, in which a large number of transmit antennas are used at the base sta- tion to simultaneously serve multiple receivers [3]. Nonlin- ear precoding methods such as dirty paper coding are performance achieving. However, these precoding are highly complex, thereby motivating the need for linear methods, which are computationally simpler. Channel inversion-based linear precoding algorithms such as zero- forcing channel inversion (ZF-CI) can still be used to cancel the MUI with the lower complexity. As the generalization * Correspondence: jing401@126.com 2Tianjin Key Laboratory of Wireless Mobile Communications and Power Transmission, Tianjin Normal University, Tianjin 300387, China Full list of author information is available at the end of the article of the ZF-CI precoding algorithm, the block diagonalization (BD) and regularized block diagonalization (RBD) precod- ing have been proposed for MU-MIMO systems in [4–6]. Singular value decomposition (SVD) operations are imple- mented twice for each user in BD precoding algorithm. Over the last few years, many works have analyzed the zero-forcing beamforming for single-stream transmis- sion per user and the zero-forcing precoding for mul- tiple streams per user as the generalized single antenna [7–10]. As to the analysis of multiple streams, some re- searches for MU-MIMO focused on zero-forcing pre- coding, and it is noted that most of the previous works on BD precoding assumed designing the BD-type precoding schemes with less computational complexity. QR-decomposition-based BD (QR-BD), generalization ZF-CI (GZI), and lattice reduction (LR)-assisted precod- ing are proposed in [11–14]. For the multiple streams system, we must do power control or the adaptive modulation and coding to balance the effective channel gain for each stream [15, 16], which gets the same SNR for much channel with the geometric mean decompos- ition (GMD); otherwise, the performance of each user will suffer significant loss. However, the power control or adaptive modulation is hard to achieve especially in the multiple antennas systems, suffering from high com- plexity and large signaling overhead. © 2016 The Author(s). Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 2 of 7 antennas (as shown in Fig. 1). Each BS simultaneously serves K number of lk-antennas users. Without loss of generality, we assume that the received antenna number lk for each user is the same. We consider a flat fading channel, we further assume that the channel state in- formation (CSI) is perfectly known at the transmitter, and synchronization between the BS and the users is assumed. The channel matrix coupling the BS to the user is of the kth user set and modeled as the flat Rayleigh fading MIMO channel: H k ¼ h11 h12 ⋯ h1M h21 h22 ⋯ h2M ⋮ ⋮ ⋱ ⋮ hlk 1 hlk 2 ⋯ hlkM ð1Þ where H k∈ℂ lkM is MIMO channel matrix for the user k and the element hu,v indicates the channel impulse re- sponse coupling the k transmit antenna to the received antenna. The system channel matrix is as follows: H ¼ H T H T 2 ⋯ H T k 1 T XK i¼1;i≠k ð2Þ ð3Þ The received signal yk for user k is given by: yk ¼ H kPksk þ H k Pisi þ nk k ⋯ srk k sk ¼ where Pk is the precoding matrix for user k. s1 k s2 is the transmission symbol vector for the kth user set, rk ≤ lk. nk is the kth user’s additive white Gauss- ian noise (AWGN) with zero-mean and σ2 variance, that is, CN (0, σ2) for all user terminals. P ¼ P1 P2 ⋯PK ½ T S ¼ sT ⋯sT K ð4Þ ð5Þ where P ∈ ℂM × t and S are the precoding matrix and the sT 2 1 In the following, we propose a new linear precoding scheme based on BD for a downlink MU-MIMO systems with multiple data streams per user. The design goal is simple and a low-complexity algorithm to compute the precoding matrix for each user without the power control. To do this, we introduce a slight relaxation for BD pre- coding with once SVD. Thereby, we obtain a general form which simultaneously diagonalizes covariance matrices through independently precoding. The contribution of this work is that we develop a new BD precoding for downlink MU-MIMO system with multiple data streams per user to improve the BER performance without complex power, modulation, or coding. As detailed in the paper, the proposed algorithm is based on the multiple users and multiple streams MIMO systems which will be finally used for the deriv- ation of the analytical system performance. A more thor- ough evaluation of proposed algorithm is confirmed via simulations. Furthermore, the new algorithm demon- strates a superiority performance. The rest of the paper is organized as follows. Section 2 introduces the system model of MU-MIMO downlink transmissions. Then, the proposed maximum ratio transmission (MRT) precoding algorithm is detailed in Section 3. To examine the proposed transmission strat- egy in an efficient manner, a system-level simulator is designed. The benefits of the proposed transmission strategy are demonstrated through numerical simula- tions in Section 4. Finally, concluding remarks are drawn in Section 5. We briefly summarize the notations used in this paper. Uppercase boldfaced letters are used to denote matrices and lowercase boldfaced letters for vectors. The super- scripts ()T, ()*, ()H note the transpose, conjugate, and conjugate transpose, respectively. 2 System model 2.1 System model Consider downlink MU-MIMO system with one BS equipped with M transmits antennas and N received Fig. 1 MU-MIMO system model

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 3 of 7 transmit signal for K users, respectively. The total data stream for K users is t, and t ≤ rank (H). 2.2 MUI as interference We can consider the MUI as an additive interference, af- fecting the useful signal. The useful symbol is weighted by the equivalent channel frequency response, which is the sum of random variables of channels. In Eq. (3), H k pisi is the MUI contribution. In this paper, XK i¼1;i≠k the interference models based on classical approxima- tion or on other distributions are assumed to be inde- pendent from the useful term. 3 Precoding scheme 3.1 BD precoding algorithms As the generalization of the ZF precoding algorithm, the design of BD-based precoding algorithms is performed in two steps [4, 17]. Two SVD operations are implemented for each user in the BD precoding algorithm. The first SVD eliminate completely the MUI from other users for MU-MIMO channel. Thus, the MU-MIMO channel is decomposed into multiple parallel single-user MIMO (SU-MIMO) channels. The second SVD operation is im- plemented to parallelize each user’s streams and obtain maximum precoding gain for each sub-stream to further improve the performance. Precoding matrix for the sys- tem is the product of the matrixes of the two steps. The interference channel matrix for the kth user. ð6Þ ~H k ¼ H T In order to eliminate completely the MUI, that is HiPk ⋯ H T K ⋯ H T T kþ1 H T k−1 1 = 0, i ≠ k, Pk in the zero space of ~H k. SVD decomposition for ~H k. H ~H k ¼ ~U k ~Σ k ~V k 1ð Þ ~V k 0ð Þ ð7Þ 1ð Þ k 0ð Þ where ~V is the right-singular matrix with non-zero sin- gular value and ~V k is the right-singular matrix with zero singular value. When the BD algorithm is employed as the precoding technique, single-user channel matrix after the MUI elimination is shown. Therefore, ~V k is the zero space of ~H k. the equivalent The equivalent channel of the kth user can be given 0ð Þ as: 0ð Þ ð8Þ H effk ¼ Hk ~V k When the BD algorithm is employed, the norm of the equivalent channel after precoding equals the norm of 2 the projected channel. F ¼ Hi 2 F i ¼ 1; ⋯K H i ~V i ð9Þ ~P i ½ H where ~P i is a projection matrix that serves to the chan- nel matrix of the user of i. 1ð Þ V k 0ð Þ ¼ Uk Σk 0 The SVD decomposition for Heffk is: V k H effk ¼ Hk ~V k in the same way, where the right-singular matrix with 1ð Þ non-zero singular value is V k is the right- singular matrix with zero singular value. The precoding vector can be written as: 1ð Þ ⋯ ~V K P ¼ ~V 1 0ð Þ and V k ð11Þ ð10Þ 0ð ÞV K 0ð ÞV 1 1ð Þ 0ð Þ ð12Þ ð13Þ y ¼ HPx þ n ¼ Therefore, the relation (3) will be rewritten. 1 Ax þ n 1 Ax þ n H 1P1 ⋯ H 1PK H K P1 ⋯ H K PK H 1P1 ⋯ ⋮ ⋱ 0 ⋯ H K PK 0 @ 0 @ ¼ ⋱ 0 ⋮ ⋮ ⋮ XK The receive vector of the kth user can be given as: yk ¼ HkPkxk þ HiPixi þ nk i≠k k Thus, from (13), the interference is eliminated com- Dk ¼ U H pletely. The kth user’s decoding matrix is expressed as: ð14Þ BD precoding provides better performance due to the unitary precoding. However, the drawback of such pre- coding scheme-based BD is that the effective channel gain for each stream is severely destroyed by the inter- ference. It is known that the overall performance of a user with multiple streams is dominated by the stream with the worst channel condition. Hence, interference would lead to poor overall error performance for a user. In the next section, we design a new precoding scheme so as to overcome this drawback. 3.2 Proposed precoding For the conventional BD precoding, the interferences are involved in the received signals. This will be a key aspect and have to be specifically studied in our study. In the following, we drive a new BD precoding by con- structing the interference matrix independently in a MU-MIMO system using QPSK modulation. We focus on the two-user and three-user cases to provide analysis. The further study will give the new information about the arbitrary number of antennas. Firstly, calculate the precoding vector of each receiving antenna by the first SVD. Then, the precoding matrix of the kth user denoted Pk, which each column is calcu- lated separately for each receiving antenna.

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 4 of 7 Let us define H k to be the interference channel matrix of the ith antenna at the kth user. ð15Þ ið Þ ¼ð H H k k ið Þ H 1 ⋮ H k−1H kþ1 ⋮ H K ið Þ Þ ið Þ where H k line. H k by: ið Þ is the kth channel matrix that removed the ith can be expressed through SVD and described ið Þ ¼ U k H k ið ÞΣ k ið Þ 1ð Þ V k ið Þ 0ð Þ ið Þ V k H ð16Þ ið Þ 1ð Þ ið Þ ið Þ 0ð Þ ið Þ 0ð Þ is the right-singular matrix with non-zero is the right-singular matrix with is the zero . For the kth user, MRT precoding is given where V k singular value and V k non-zero singular value. Therefore, V k space of H k by: P k ¼ P k ð17Þ The total number of the receiver antennas is lk, the new precoding matrix of the ith receiver antenna at the ið Þ 0ð Þ lð Þ, kth user (M dimension column) denotes P k and Pk is the precoding matrix for the kth user (lk × M dimension). Further, the receiver vector at user k is writ- ten as: ið Þ ¼ V k 1ð Þ; P k 2ð Þ; …; P k lkð Þ XK i¼1;i≠k yk ¼ H kPk xk þ ¼ Ψ kxk þ nk H kPk xi þ nk ð18Þ where the first part is the coefficient of the receiver an- tenna at user k, Ψ k ¼ H kPk (lk is the dimension column), the second part is the MUI, and H kPi is zero obviously. So, the interference of the antenna of equivalent channel is eliminated. Then, the maximal ratio combination (MRC) for the received symbols for the entire antenna at user k is writ- ten as: yk ¼ yk ið Þ⋅Ψ k ið Þ ð19Þ Xlk i¼1 Finally, the estimated result at user k is get, through the hard decision for the received symbol yk. 4 Simulation results In this section, we investigate the performance of the pro- posed scheme for MU-MIMO downlink system by means of Monte-Carlo simulations, comparing it with the original proposed BD precoding. A spatially uncorrelated flat Ray- leigh fading of the wireless channel is assumed, and the noise distributed complex Gaussian variables with zero- mean and unit-variance, considering quadrature phase shift keying (QPSK) modulation. For simplicity but without loss of generality, we consider that the number of received antennas for each user is the same, which equal to the total data streams of the transmit user. Then, we study the performance of the MU-MIMO system for the differ- ent antenna configuration by simulations. We com- pare the simulated bit error rate (BER) in a MU-MIMO system with different system transmission and the antenna configuration. 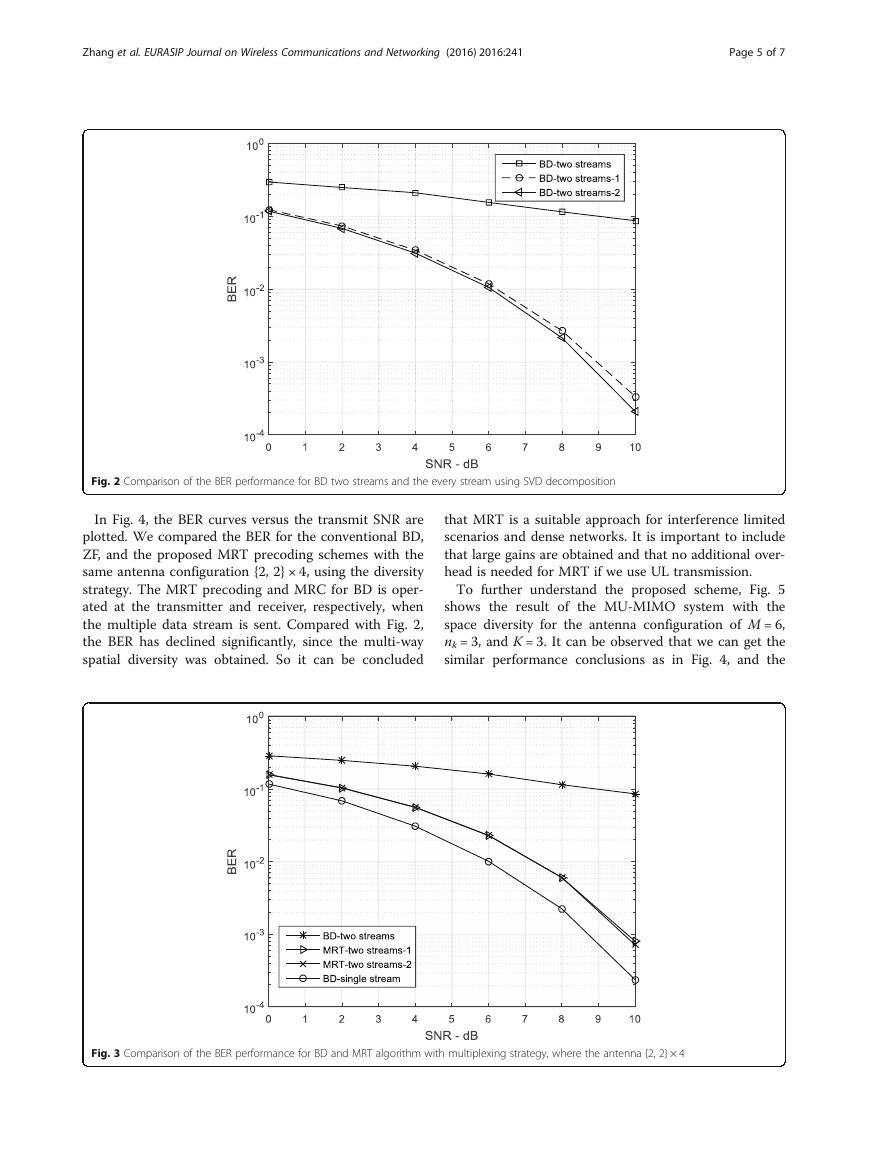Figure 2 compares the BD precoding with two streams and every stream using SVD decomposition. The BD pre- coding scheme operate two SVD for each user and the interference is introduced, so the performance highly af- fected by the worst channel conditions for multi-streams transmission. Because BD precoding algorithm effective channel gains unbalance between different data flows, it leads to the poor performance of the system. It can be observed that as SNR increased, the performance of BER improved obviously for the SVD decompos- ition of each stream. This shows that the interference is influenced by the system performance even with a low SNR, then the performance would be worse than the once SVD decomposition. By comparing the performance of BD precoding of two streams, we can summarize the conclusion, and a significant interference is introduced in the BD precod- ing. It is observed in simulation conditions. So, it can be concluded that BD precoding is not a suitable approach for MUI scenarios and dense network. It is important to recall that gains are obtained even in SVD decompos- ition only once and as SNR is increased, higher impact of interference on performance is observed. But in MU- MIMO systems, the MUI is also important. 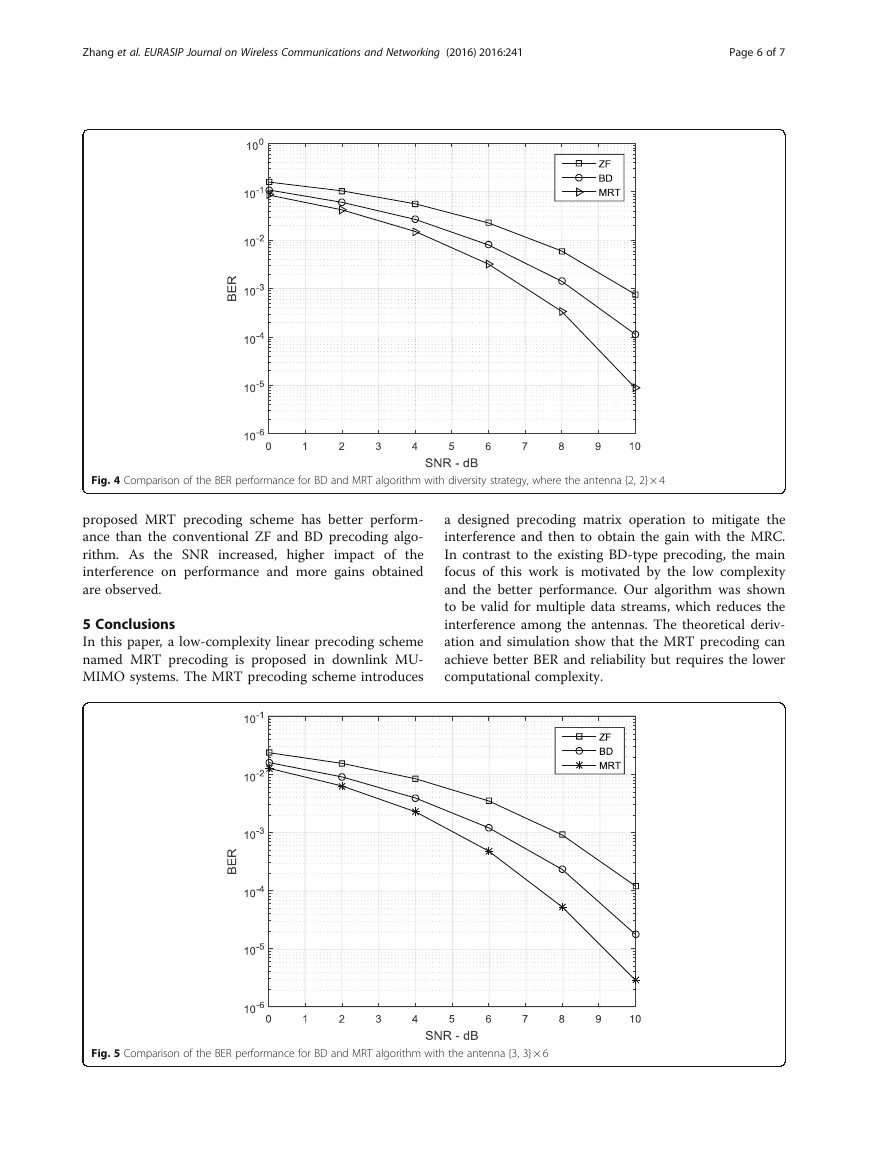As is shown in Fig. 3, we compare the BER for every stream when an MRT is used for transmission from BS to the UEs. The BER curves are plotted versus the transmit SNR with the antenna configuration for {2, 2} × 4, M = 4, nk = 2, and K = 2. We compared the BER for the conven- tional BD and the proposed MRT precoding schemes with the same antenna configuration, using the multiplexing strategy. As expected, the proposed MRT precoding scheme performs better BER than the conventional BD precoding algorithm. Because the BD precoding scheme operate two SVD and the interference is introduced, there- fore, the performance of single data stream is better than multiple data streams for BD precoding scheme. The MRT precoding SVD operation only once and therefore reduces the interference and computational complexity.

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 5 of 7 Fig. 2 Comparison of the BER performance for BD two streams and the every stream using SVD decomposition In Fig. 4, the BER curves versus the transmit SNR are plotted. We compared the BER for the conventional BD, ZF, and the proposed MRT precoding schemes with the same antenna configuration {2, 2} × 4, using the diversity strategy. The MRT precoding and MRC for BD is oper- ated at the transmitter and receiver, respectively, when the multiple data stream is sent. Compared with Fig. 2, the BER has declined significantly, since the multi-way spatial diversity was obtained. So it can be concluded that MRT is a suitable approach for interference limited scenarios and dense networks. It is important to include that large gains are obtained and that no additional over- head is needed for MRT if we use UL transmission. To further understand the proposed scheme, Fig. 5 shows the result of the MU-MIMO system with the space diversity for the antenna configuration of M = 6, nk = 3, and K = 3. It can be observed that we can get the similar performance conclusions as in Fig. 4, and the Fig. 3 Comparison of the BER performance for BD and MRT algorithm with multiplexing strategy, where the antenna {2, 2} × 4

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 6 of 7 Fig. 4 Comparison of the BER performance for BD and MRT algorithm with diversity strategy, where the antenna {2, 2} × 4 proposed MRT precoding scheme has better perform- ance than the conventional ZF and BD precoding algo- rithm. As the SNR increased, higher impact of the interference on performance and more gains obtained are observed. 5 Conclusions In this paper, a low-complexity linear precoding scheme named MRT precoding is proposed in downlink MU- MIMO systems. The MRT precoding scheme introduces a designed precoding matrix operation to mitigate the interference and then to obtain the gain with the MRC. In contrast to the existing BD-type precoding, the main focus of this work is motivated by the low complexity and the better performance. Our algorithm was shown to be valid for multiple data streams, which reduces the interference among the antennas. The theoretical deriv- ation and simulation show that the MRT precoding can achieve better BER and reliability but requires the lower computational complexity. Fig. 5 Comparison of the BER performance for BD and MRT algorithm with the antenna {3, 3} × 6

Zhang et al. EURASIP Journal on Wireless Communications and Networking (2016) 2016:241 Page 7 of 7 Acknowledgements This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grant 61501325, 61362027, and 61461036, the Natural Science Foundation of Inner Mongolia Autonomous Region of China under Grant 2016MS0604, and the Doctor Foundation of Tianjin Normal University under Grant 52XB1507. Competing interests The authors declare that they have no competing interests. Author details 1College of Electronic Information Engineering, Inner Mongolia University, Hohhot 010020, China. 2Tianjin Key Laboratory of Wireless Mobile Communications and Power Transmission, Tianjin Normal University, Tianjin 300387, China. Received: 29 July 2016 Accepted: 20 September 2016 References 1. Z Gao, L Dai, MmWave massive-MIMO-based wireless backhaul for the 5G ultra-dense network. IEEE Wirel. Commun. 21(5), 13–21 (2015) QH Spencer, AL Swindlehurst, M Haardt, An introduction to the multi-user MIMO downlink. IEEE Commun. Mag. 42(10), 60–67 (2004) H Sung, S Lee, I Lee, Generalized Channel Inversion Methods for Multiuser MIMO Systems. IEEE Trans. Commun. 57(11), 3489-3499 (2009) QH Spencer, AL Swindlehurst, M Haardt, Zero-forcing methods for downlink spatial multiplexing in multi-user MIMO channels. IEEE Trans. Signal Process. 52(2), 461–471 (2004) V Stankovic, M Haardt, Generalized design of multi-user MIMO precoding matrices. IEEE Trans. Wirel. Commun. 7(3), 953–961 (2008) V Stankovic, M Haardt, “Linear and nonlinear multi-user MIMO precoding,” presented at the WWRF, Shanghai, China, Nov. 2006, WWRF Paper 16, 2006 J Wu, S Fang, L Li et al., QR decomposition and gram Schmidt orthogonalization based low-complexity multi-user MIMO precoding, in Wireless Communications, Networking and Mobile Computing (WiCOM), 2014, pp. 61–66 H Fu, M Crussiere, M Helard, BER analysis for equal gain transmission in downlink multiuser MIMO systems. IEEE Wireless Commun. Lett. 4(5), 533–536 (2015) S Zarei, W Gerstacker, R Schober, Low-complexity widely-linear precoding for downlink large-scale MU-MISO systems. IEEE Commun. Lett. 19(4), 665–668 (2015) 2. 3. 4. 5. 6. 7. 8. 9. 10. C Feng, Y Jing, S Jin, Interference and outage probability analysis for massive MIMO downlink with MF precoding. IEEE Trans. Signal Process. 53(7), 665–668 (2015) 11. H Sung, SR Lee, I Lee, Generalized channel inversion methods for multiuser 12. 13. 14. MIMO systems. IEEE Trans. Commun. 57(11), 3489–3499 (2009) K Zu, RC De Lamare, M Haardt, Generalized design of low-complexity block diagonalization type precoding algorithms for multiuser MIMO systems. IEEE Trans. Commun. 57, 4232–4242 (2013) S Fang, J Wu, C Lu et al., Simplified QR-decomposition based and lattice reduction-assisted multi-user multiple-input-multiple-output precoding scheme. IET Commun. 10(5), 586–593 (2015) S Lagen, A Agustin, J Vidal, Decentralized coordinated precoding for dense TDD small cell networks. IEEE Trans. Wirel. Commun. 14(3), 4546–4561 (2015) 15. Y Cheng, S Li, J Zhang et al., An efficient transmission strategy for the multicarrier multiuser MIMO downlink. IEEE Trans. Veh. Technol. 63(2), 628–642 (2014) 16. D Lee, Performance analysis of zero-forcing-precoded scheduling system 17. with adaptive modulation for multiuser-multiple input multiple output transmission. IET Commun. 9(16), 2007–2012 (2015) LU Choi, RD Murch, A transmit preprocessing technique for multiuser MIMO systems using a decomposition approach. IEEE Trans. Wirel. Commun. 3(1), 20–24 (2004) Submit your manuscript to a journal and beneﬁ t from: 7 Convenient online submission 7 Rigorous peer review 7 Immediate publication on acceptance 7 Open access: articles freely available online 7 High visibility within the ﬁ eld 7 Retaining the copyright to your article Submit your next manuscript at 7 springeropen.com

分享到：

赞收藏

资料库

下行链路多用户MIMO系统中的MRT预编码.pdf

相关推荐

开发技术

热门标签

最新资料