基于积分原理的储油罐变位识别与罐容表标定 .pdf-资料库

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第1页.png

第1页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第2页.png

第2页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第3页.png

第3页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第4页.png

第4页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第5页.png

第5页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第6页.png

第6页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第7页.png

第7页 / 共18页

c67dcd0e-aabb-44d8-9720-db2e3bf38c3a.pdf-第8页.png

第8页 / 共18页

中国科技论文在线 http://www.paper.edu.cn 基于积分原理的储油罐变位识别与罐容表标定樊宇1，王宇楠2，王俊杰3，曹奇3* （1. 河海大学土木与交通学院，南京 210098）； 2. 河海大学港口海岸与近海工程学院，南京 210098）； 3. 河海大学地球科学与工程学院，南京 210098）摘要：针对储油罐的变位识别与罐容表标定的问题，本文建立了椭圆形平头储油罐计算模型、圆形球缺顶储油罐计算模型和最小二乘法搜索模型等三个计算模型。首先，对截面进行积分，给出了当纵向倾斜角α取 0°至 4.1°时平头罐内油位高度 h 与储油量 V 的函数关系式。再者，为了计算圆形球缺顶罐头体积，采用化斜为正和拆左补右的方法，求出倾斜时的球缺体积并最终得到 V 关于参数α、β、h 的表达式。在最小二乘法搜索模型中，提出了总偏差 F（α、β）的概念，将参数α、β的求解问题转化为最优化问题，通过逐步缩小参数范围提高其精度并得最优解。最后，通过 MATLAB 拟合得到三个模型的误差校正函数，经过误差分析发现：误差校正函数主要与油液度数 h、参数α及β有关，此外，在油液体积较大且温度较高时，还受温度 T 影响。关键词：罐容表；微积分；最小二乘法；误差分析；变位识别中图分类号：TE822 Displacements Recognition of Storage Tank and Calibration of Tank Capacity Charts Based on Integration Fan Yu1, Wang Yunan2, Wang Junjie3, Cao Qi3 (1. College of Civil and Transportation Engineering,Hohai University, NanJing 210098; 2. College of Harbour,Coastal and Offshore Engineering,Hohai University, NanJing 210098; 3. School of Earth Sciences and Engineering,Hohai University, NanJing 210098) Abstract: In this paper, to identify the displacements and tank capacity charts calibration, the oval crew-cut oiltank computing model, round ball top oiltank computing model and least-square searching model are established. By integrating the section , the paper is first concerned with the function expression of oil level height h and storage volume V in the crew-cut oil tank, when longitudinal angle α varies from 0 ° to 4.1 °. When the round ball top is sloped, this paper utilizes two special ideas to compute the volume of round ball top and finally to obtain the expression V with respect to parameter α and parameter β and h. In least squares searching model, the paper introduces the concept of the total deviation F (α, β), in which the solving problem of the parameter α and β becomes an optimization problem. By gradually narrowing parameter scope, the accuracy can be improved and the optimal solution can furthermore be presented. With the aid of MATLAB, this article also finally presents error correction function of three models. Error analyses indicate that error correction function are mainly related with oil height h, parameter α and parameterβ. In addition, it is influenced by temperature T , as the oil volume is larger and the temperature is high. Keywords:Tank capacity charts; Integration; Least-square method; Error analysis; Displacements recognition 0 问题重述通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的作者简介：樊宇，男，（1989-），本科生，河海大学土木工程专业. E-mail: fanyu.2010.1@gmail.com - 1 -

中国科技论文在线 http://www.paper.edu.cn 罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。按照有关规定，需要定期对罐容表进行重新标定。图 1 是一种典型的储油罐尺寸及形状示意图，其主体为圆柱体，两端为球冠体。图 2 是其罐体纵向倾斜变位的示意图，图 3 是罐体横向偏转变位的截面示意图。请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。（1）为了掌握罐体变位后对罐容表的影响，利用如图 4 的小椭圆型储油罐（两端平头 °1.4 的纵向变位两种情况做了实验，实验的椭圆柱体），分别对罐体无变位和倾斜角为α= 数据如附件 1 所示。请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为 1cm 的罐容表标定值。（2）对于图 1 所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β ）之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据（附件 2），根据你们所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为 10cm 的罐容表标定值。进一步利用附件 2 中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。注：相关参考图及附件见原题。 1 问题分析在计量测定单位或者石油存储单位，储油罐的储油量与罐内油位高度关系一直是热点问题。但是，大部分人研究的只是水平卧式储油罐储油体积与油位高度问题，对倾斜变位的储油罐储油量与油位高度问题的研究涉及很少。本文通过球体几何关系和高等数学中积分知识进行公式的推导，对推出的公式用数学软件(MATLAB，mathematica 等)进行验证和修正， - 2 -

中国科技论文在线 http://www.paper.edu.cn 对实验得出的数据进行误差分析和改正，使实验数据尽量接近理论数据。对于αβ参数的确定，本文运用最小二乘法通过计算机编程不断缩小参数αβ范围，最后得到符合条件的 αβ的最优解。 2 模型假设 1. 表格中储油罐的进出油量数据准确。 2. 油位计的标尺刻度准确。 3. 油位的高度等于油位计读数。 4. 储油罐的变位会导致油罐的挤压形变。 3 符号系统 h ：油浮子到罐底的距离，油位高度，油位计读数； V ：储油罐的储油量； 0V ：无变位时储油罐储油量； 1V ：变位时储油罐储油体量； VΔ ：实验得出的储油量与理论储油量之差； xzS ：液体与 xoz 平面平行的截面积； 1h ， 2h ：液面与左右封头交点到罐底距离； 0h ：液体截面到罐底距离；左V ，右V ：储油罐左右端球缺部分体积； βα, ：分别指纵向倾斜角和横向倾斜角； H ：储油罐一端球顶到封头的距离； r ：储油罐球缺部分的球的半径； R ：储油罐缺面的半径； ( βαF ) ：改正值 ′Δ iV 与测量值 iVΔ 的总偏差； , 4 模型建立 4.1 椭圆型平头储油罐计算模型本模型推导储油罐剩于油料高度 4.1.1 储油罐水平时的情况 −∈hh ])6.0,6.0[ ( 与储油量V 的计算公式。为了简便计算，我们考虑椭圆形储油罐（两端平头的椭圆柱体）罐体无变位时罐内油位高度 h 与储油量V 的对应关系[1]，建立如图 5 所示的空间直角坐标系。 - 3 -

中国科技论文在线 http://www.paper.edu.cn 图 5 小椭圆型储油罐无变位时储油量V 的计算罐体内油料剩余体积相当于椭圆柱体的一部分，将这一部分在 ZX 0 截面的投影记为 xzS ，如图 6，则 xzS 为此部分的底面。图 6 xzS 面积的计算显然， V •= xzSL 根据题意已知 45.2=L )1( ，只需计算截面面积 xzS ，利用积分[2]， dS xz = 2 xdx = a (2 b 2 b − z ) 22 dz + xz S = ab π 2 所以， h ∫ 0 2 a b 2 b − 2 z dz = ab π 2 arctan( bh a b + − 2 h + 2 b ( h − 2 b h 2 计算定积分， )) 2 )2( hV )( 0 •= SL xz = L ab π 2 + aL b ( bh 2 − 2 h + 2 b arctan( h − 2 b 2 h )) h −∈ ]6.0,6.0[ )3( 代入数值 a=0.89m,b=0.6m,得到罐体体积为 hV )( 0 = .045.2 ⎡ ⎢ ⎣ 8388 + 534.0 Arc sin( h 6.0 .0)1 +− (534 h 6.0 − (1)1 − h 6.0 2 − )1 通过 MATLAB[3]绘制 )(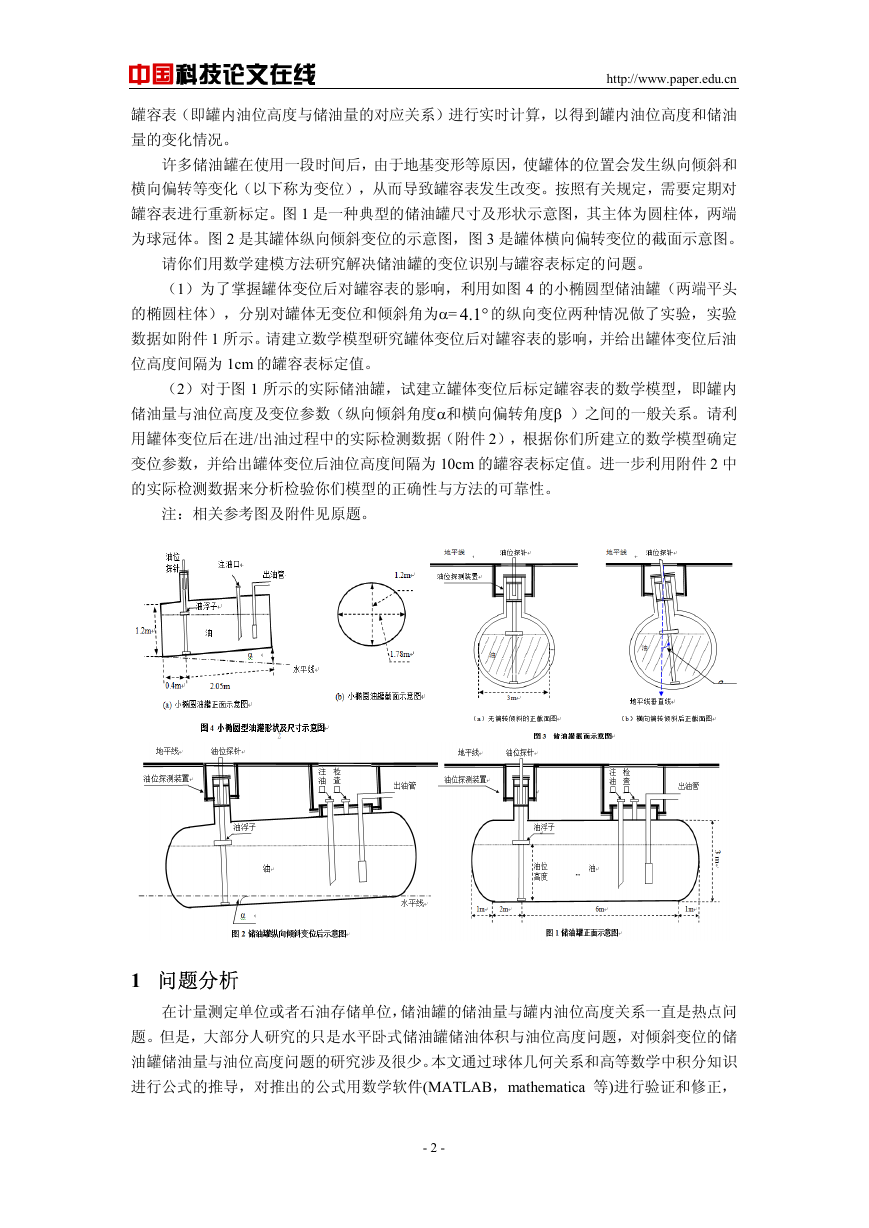0 hV 曲线及附录一中储油罐无变位时实验数据曲线如图 7。 ⎤ ⎥ ⎦ )4( - 4 -

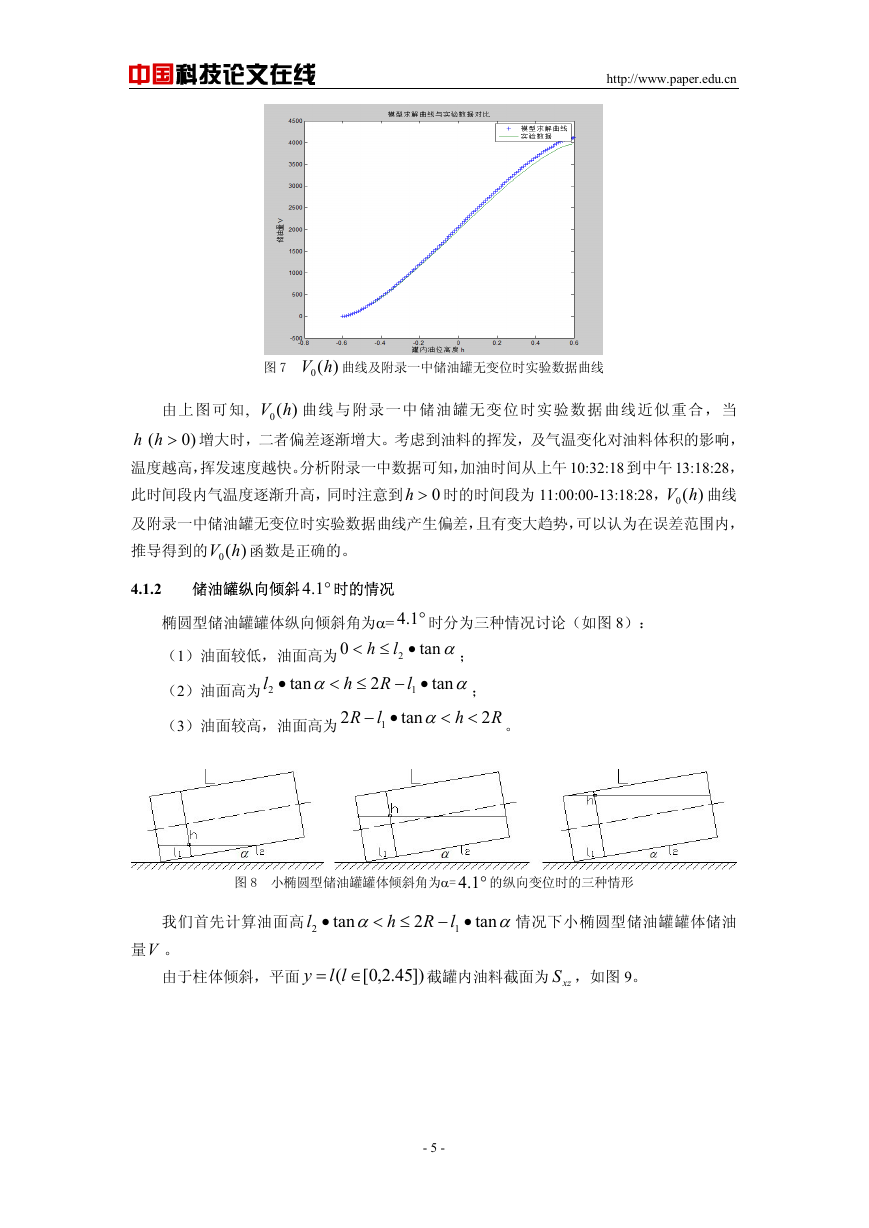
中国科技论文在线 http://www.paper.edu.cn 图 7 )(0 hV 曲线及附录一中储油罐无变位时实验数据曲线 )(0 hV 曲线与附录一中储油罐无变位时实验数据曲线近似重合，当由上图可知, ( >h )0 h 增大时，二者偏差逐渐增大。考虑到油料的挥发，及气温变化对油料体积的影响，温度越高，挥发速度越快。分析附录一中数据可知，加油时间从上午 10:32:18 到中午 13:18:28，此时间段内气温度逐渐升高，同时注意到 0>h 时的时间段为 11:00:00-13:18:28， )(0 hV 曲线及附录一中储油罐无变位时实验数据曲线产生偏差，且有变大趋势，可以认为在误差范围内，推导得到的 )(0 hV 函数是正确的。 4.1.2 储油罐纵向倾斜 °1.4 时的情况 °1.4 时分为三种情况讨论（如图 8）：椭圆型储油罐罐体纵向倾斜角为α= l （1）油面较低，油面高为 α （2）油面高为 tan • l 2 （3）油面较高，油面高为 αtan tan h 0 h 2 ≤< lR 2 1 2 •≤< lR •− 1 tan •− ； α h ； 2 α << R 。图 8 小椭圆型储油罐罐体倾斜角为α= °1.4 的纵向变位时的三种情形我们首先计算油面高 l 2 • tan 量V 。 α ≤< h lR •− 1 2 tan α 情况下小椭圆型储油罐罐体储油由于柱体倾斜，平面 y ( ∈= ll ])45.2,0[ 截罐内油料截面为 xzS ，如图 9。 - 5 -

中国科技论文在线 http://www.paper.edu.cn 图 9 油面高 l 2 • tan α ≤< h lb 2 •− 1 tan α 下储油量V 的计算若得到 xzS 关于 y 的函数关系式，则 y∫= V dy S xz 0 )5( 图 10 截面 xzS 中油液面高度 0h 的计算 h − y ) 4.0( += 当 y 取不同值时，截面 xzS 的面积也随之变化，设 0h 表示截面 xzS 中油液面高度，则， h tan α• 0 利用微积分计算 xzS ，有 dS xz − xdx )6( ) 22 dz 2 b = = 2 z 2 b − 2 z dz = ab π 2 + a b ( h 0 2 b − 2 h 0 + 2 b arctan( h 0 − 2 b 2 h 0 )) )7( a (2 b a b 2 h 0 ∫ 0 S xz = ab π 2 + 所以， hV )( = = 45.2 45.2 0 ∫ ∫ 0 dy S xz ab π 2 + a b ( h 0 2 b − 2 h 0 + 2 b arctan( h 0 − 2 b 2 h 0 dy )) )8( 下面计算油面高 h αtan•≤ l 情况下小椭圆型储油罐罐体储油量V 。图 11 油面高 h αtan•≤ l 下储油量V 的计算 - 6 -

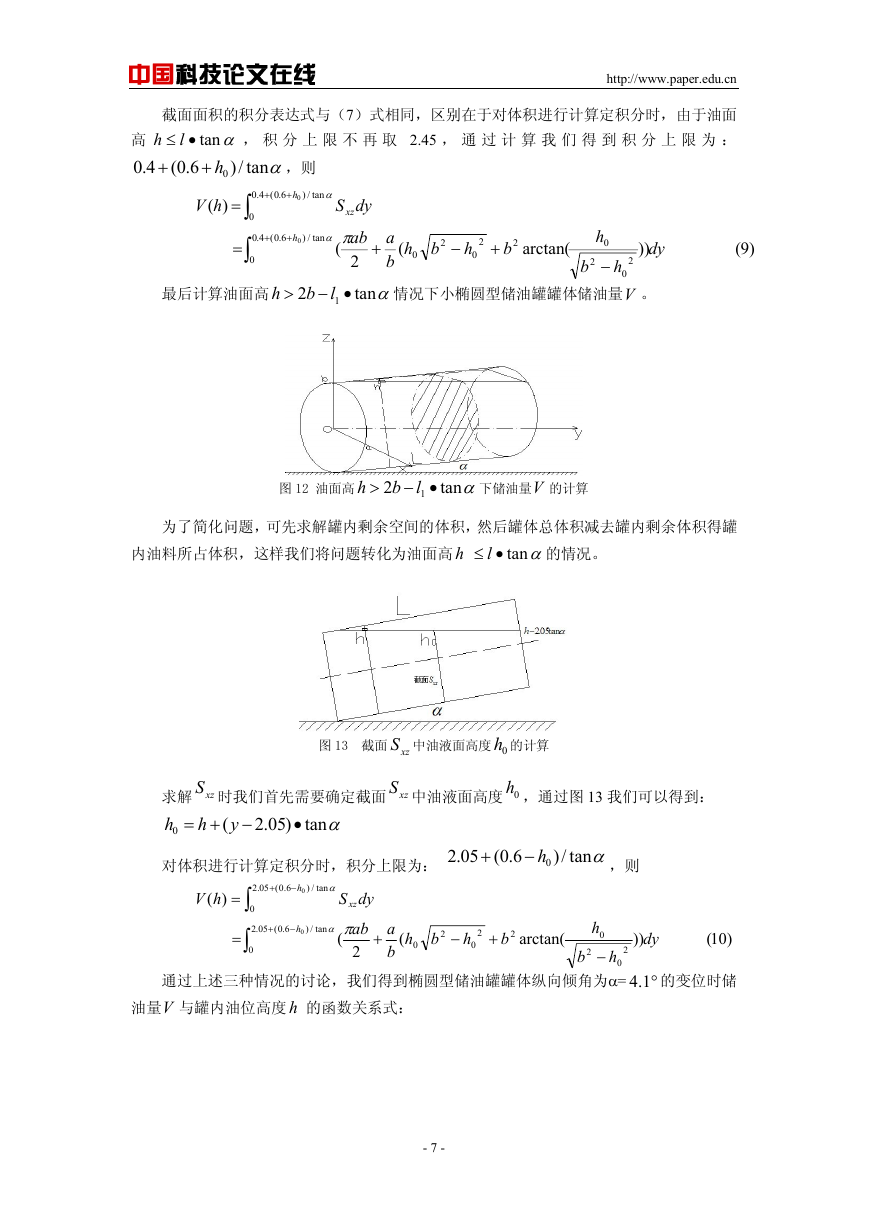
中国科技论文在线 http://www.paper.edu.cn 高 6.0(4.0 截面面积的积分表达式与（7）式相同，区别在于对体积进行计算定积分时，由于油面 αtan•≤ l h ，积分上限不再取 2.45 ，通过计算我们得到积分上限为： 0h+ + hV )( ，则 h 0 tan/) α + h 0 α tan/) S dy xz ab a π ( b 2 lb 2 αtan 情况下小椭圆型储油罐罐体储油量V 。 1 •− arctan( h 0 − h 0 h 0 h 0 + − + b b b ( 2 2 2 2 2 dy )) )9( = αtan/) 6.0(4.0 + ∫ ∫ 6.0(4.0 = + 0 0 + 最后计算油面高 h > 图 12 油面高 h > lb 2 αtan 1 •− 下储油量V 的计算为了简化问题，可先求解罐内剩余空间的体积，然后罐体总体积减去罐内剩余体积得罐内油料所占体积，这样我们将问题转化为油面高 h αtan•≤ l 的情况。图 13 截面 xzS 中油液面高度 0h 的计算求解 xzS 时我们首先需要确定截面 xzS 中油液面高度 0h ，通过图 13 我们可以得到： h 0 )05.2 += − h y • ( αtan 对体积进行计算定积分时，积分上限为： 05.2 + 6.0( 0h− αtan/) ，则 hV )( = 05.2 + 6.0( − h 0 tan/) α 05.2 + 6.0( − h 0 tan/) α 0 ∫ ∫ 0 = S dy xz ab π ( 2 + a b h 0 通过上述三种情况的讨论，我们得到椭圆型储油罐罐体纵向倾角为α= 油量V 与罐内油位高度 h 的函数关系式： b 2 ( h 0 2 b − 2 h 0 + 2 b arctan( h 0 − 2 dy )) )10( °1.4 的变位时储 - 7 -

中国科技论文在线 + xz S = 6.0(4.0 + 0 45.2 hV )( 1 ⎧ ∫ ⎪ ⎪ ∫ ⎨ 0 ⎪ ⎪ abL π ⎩ 其中截面 xzS 为： a b ab π 2 S xz + = − http://www.paper.edu.cn tan α h 0 tan/) α S xz dy − 6.0 ≤ h −≤ 6.0 •+ l 2 dy 05.2 + ∫ 0 − 6.0 •+ l 2 tan α •−≤< lbh 1 tan α )11( 6.0( h − 0 tan/) α ab ( π − S xz dy ) lb •− 1 tan α ≤< h 6.0 ( h 0 2 b − 2 h 0 + 2 b arctan( h 0 − 2 b )) 2 h 0 )12( 截面 xzS 中油液面高度 0h 有： tan α tan α • ) − • )05.2 4.0( y ( − + + h h h 0 = y ⎧ ⎨ ⎩ h 6.0 − lb tan •− 1 •−≤≤ 1 h ≤< lb α tan α 6.0 4.1.3 求解罐容表标定 b 代入， a m 89.0= ⎡ ⎢ ⎣ = hV )( 1 46.047.4 − (1( − 60.0= 1 3 57.0 − 6.0 = 1.4α ° 57.0 − 6.0 747.0 − 6.0 m ， h h − ，则倾斜罐容表体积： 747.0 − 6.0 (1( − 1 3 h + )) 32 Arc sin h 747.0 − 6.0 h + 57.0 − 6.0 Arc sin h + 1 − h ⎛ − ⎜ ⎝ 57.0 6.0 2 ⎞ +⎟ ⎠ 1 − 2 h ⎛ − ⎜ ⎝ 747.0 6.0 ⎞ ⎟ ⎠ ⎤ ⎥ ⎥ ⎦ )) 32 )13( )(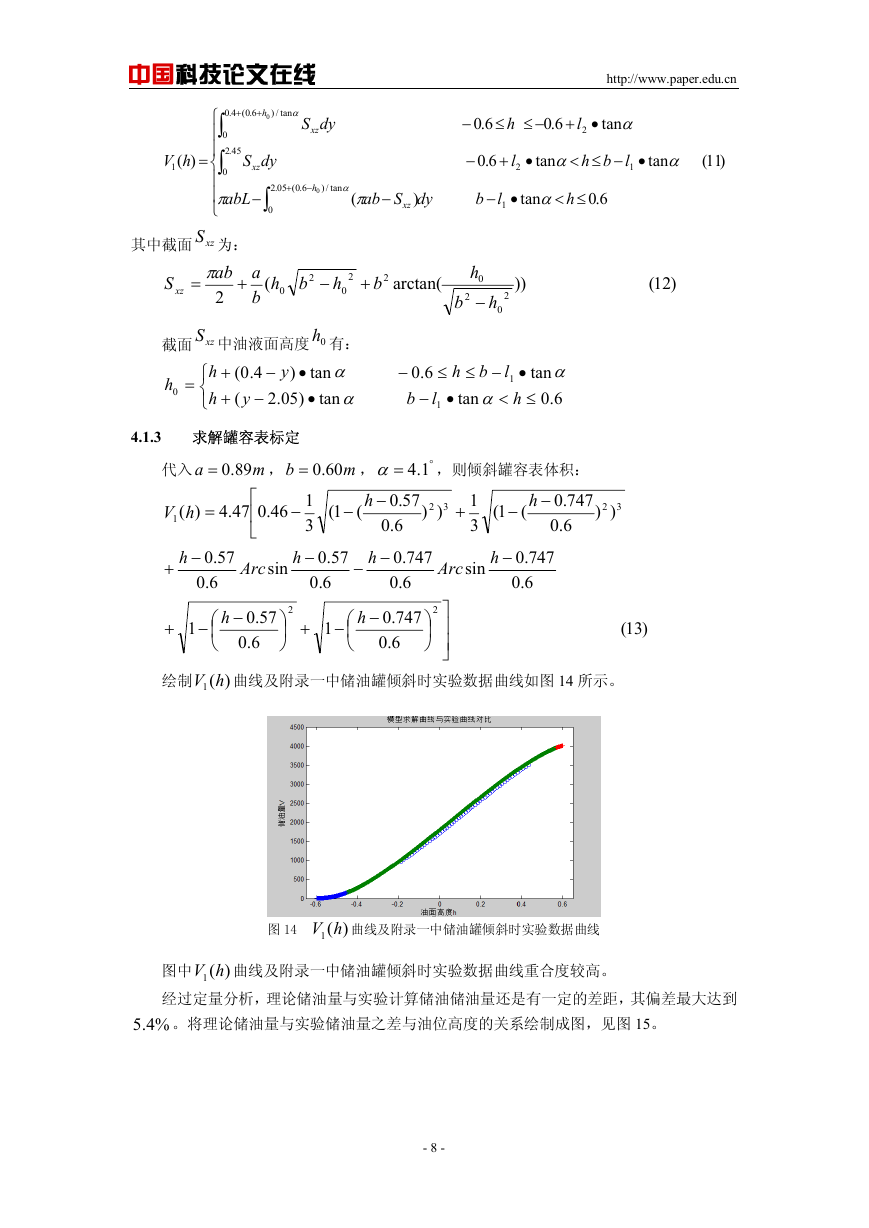1 hV 曲线及附录一中储油罐倾斜时实验数据曲线如图 14 所示。绘制图 14 )(1 hV 曲线及附录一中储油罐倾斜时实验数据曲线图中 )(1 hV 曲线及附录一中储油罐倾斜时实验数据曲线重合度较高。经过定量分析，理论储油量与实验计算储油储油量还是有一定的差距，其偏差最大达到 %4.5 。将理论储油量与实验储油量之差与油位高度的关系绘制成图，见图 15。 - 8 -

资料库

基于积分原理的储油罐变位识别与罐容表标定 .pdf

相关推荐

开发技术

热门标签

最新资料