第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
算法分析与设计实验报告之0/1背包问题.doc
[0/1背包问题]
一.问题描述
二.算法分析
1.穷举法：
2.递归法：
3.贪心法：
4.动态规划法分析：
5.回溯法分析：
6.分支限界法：
三.时空效率分析
1.穷举法：
2.递归法：
3.动态规划法：
4.回溯法：
5分支限界法：
四.运行结果
1.穷举法输出结果：
2.递归法输出结果：
3.动态规划法输出结果：
4.回溯法输出结果：
5.分支限界法输出结果：
五.分析输出结果
六.总结与反思
算法分析与设计实验报告
[0/1 背包问题]
0/1 背包问题的不同算法解决方案
组员 0945532112 黄希龙 09455321 张育强 0945532145 周麒
目录
一.问题描述....................................................................................................................................... 1
二.算法分析............................................................................................2
1.穷举法： ................................................................................................................................. 2
2.递归法： ................................................................................................................................. 4
3.贪心法： ................................................................................................................................. 5
4.动态规划法分析： .................................................................................................................6
5.回溯法分析： ......................................................................................................................... 7
6.分支限界法： ......................................................................................................................... 9
三.时空效率分析.................................................................................. 10
1.穷举法： ............................................................................................................................... 10
2.递归法： ............................................................................................................................... 11
3.动态规划法： ....................................................................................................................... 11
4.回溯法： ............................................................................................................................... 11
5 分支限界法： ....................................................................................................................... 11
四.运行结果..........................................................................................12
1.穷举法输出结果： ...............................................................................................................12
2.递归法输出结果： ...............................................................................................................13
3.动态规划法输出结果： .......................................................................................................14
4.回溯法输出结果： ...............................................................................................................15
5.分支限界法输出结果： .......................................................................................................16
五.分析输出结果.................................................................................. 17
六.总结与反思......................................................................................18
一.问题描述
0/1 背包问题:
现有 n 种物品，对 1<=i<=n，已知第 i 种物品的重量为正整数 Wi，价值为正整数 Vi，
背包能承受的最大载重量为正整数 W，现要求找出这 n 种物品的一个子集，使得子集中物
品的总重量不超过 W 且总价值尽量大。（注意：这里对每种物品或者全取或者一点都不取，
不允许只取一部分）
二.算法分析
根据问题描述，可以将其转化为如下的约束条件和目标函数：
)1(
i
n
)
i
n
Wxw
i
max
1
i
1}(1,0{
x
i
n
xv
i
i
i
1
)2(
于是，问题就归结为寻找一个满足约束条件（1），并使目标函数式（2）达到最大的
解向量
X
(
,
xxx
3
1
,
2
,......,
nx
)
。
首先说明一下 0-1 背包问题拥有最优解。
假设
(
,
xxx
1
3
,
2
,......,
nx
)
是所给的问题的一个最优解，则
(
,
xx
3
2
,......,
nx
)
是下面问题的
一个最优解：
n
2
i
x
i
xwWxw
i
i
2}(1,0{
i
11 max
n
)
n
i
2
xv
i
i
。如果不是的话，设
(
y
2
,
y
3
,......,
ny
)
是这
个 问 题 的 一 个 最 优 解 ， 则
n
i
2
yv
i
i
n
i
2
xv
i
i
， 且
xw
11
n
i
2
Wyw
i
i
。 因 此 ，
xv
11
n
i
2
yv
i
i
xv
11
n
i
2
xv
i
i
n
i
1
xv
i
i
，这说明
(
,
yx
1
2
,
y
3
,........,
ny
)
是所给的 0-1 背包问
题比
(
,
xxx
1
3
,
2
,........,
nx
)
更优的解，从而与假设矛盾。
1.穷举法：
用穷举法解决 0-1 背包问题，需要考虑给定 n 个物品集合的所有子集，找出所有可能
的子集（总重量不超过背包重量的子集），计算每个子集的总重量，然后在他们中找到价
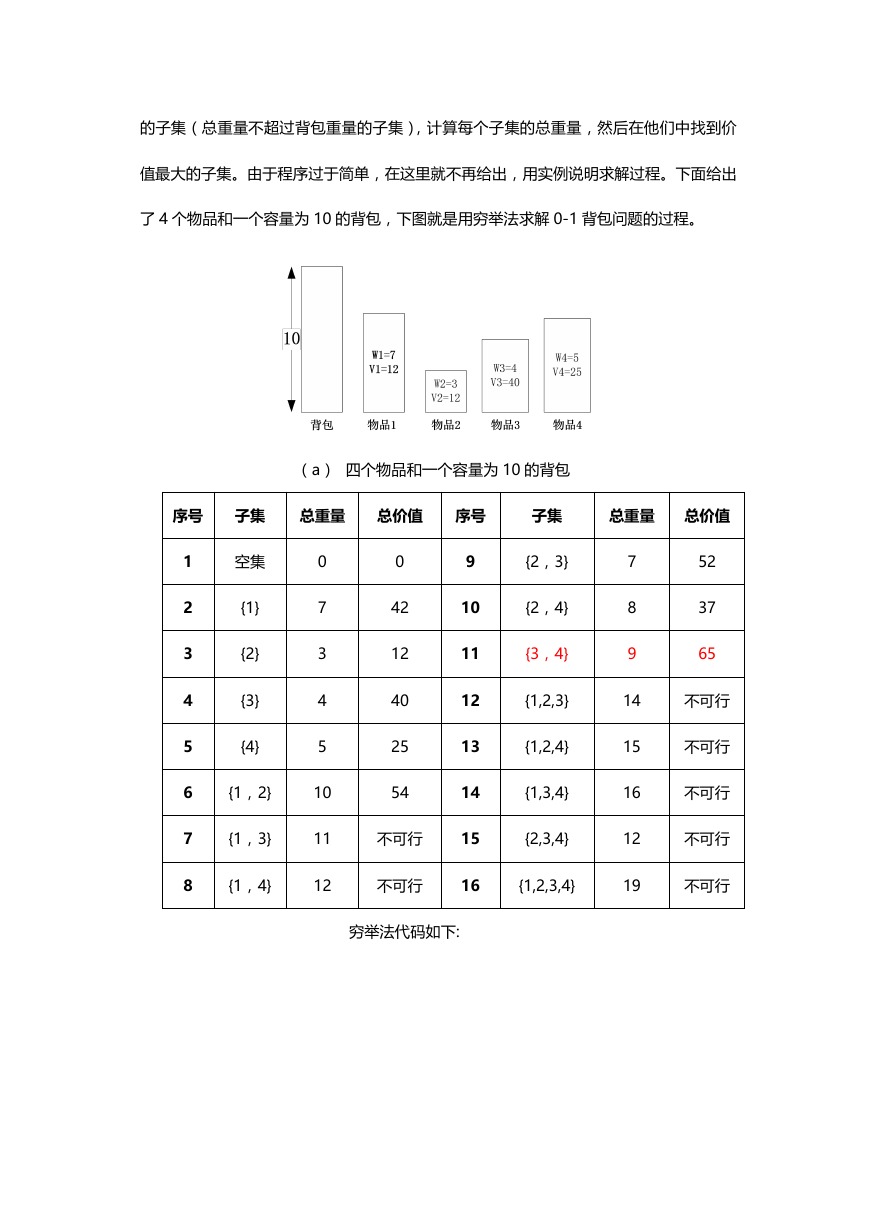
值最大的子集。由于程序过于简单，在这里就不再给出，用实例说明求解过程。下面给出
了 4 个物品和一个容量为 10 的背包，下图就是用穷举法求解 0-1 背包问题的过程。
（a） 四个物品和一个容量为 10 的背包
序号
子集
总重量
总价值
序号
子集
总重量 总价值
1
2
3
4
5
6
7
8
空集
{1}
{2}
{3}
{4}
{1，2}
{1，3}
{1，4}
0
7
3
4
5
10
11
12
9
10
11
12
13
14
15
16
{2，3}
{2，4}
{3，4}
{1,2,3}
{1,2,4}
{1,3,4}
{2,3,4}
{1,2,3,4}
7
8
9
14
15
16
12
19
52
37
65
不可行
不可行
不可行
不可行
不可行
0
42
12
40
25
54
不可行
不可行
穷举法代码如下:
#include
#include
#include
#define MAX 100 // 限定最多物品
/*将n化为二进制形式，结果存放到数组b中*/
void conversion(int n,int b[MAX])
{
int i;
for(i=0;i
子刚好相反，选择物品 n 后的价值
KnapSack
(
n
,1
[
nwm
])
][
nv
不小于不选择物品 n
情况下得到了价值
KnapSack
(
n
,1
m
)
，所以最终选择物品 n。
在递归调用的过程中可以顺便求出所选择的物品。下面是标记物品被选情况的数组
x[n]求解的具体函数表示：
][nx
0
1
KnapSack
KnapSack
,(
mn
,(
mn
)
)
KnapSack
KnapSack
(
(
n
n
,1
,1
m
[
nwm
)
])
][
nv
在函数中，递归调用的主体函数为 KnapSack，m 表示背包的容量，n 表示物品的数
量，x[n]表示是否选择了第 n 个物品（1—选，0—不选）。每个物品的重量和价值信息分
别存放在数组 w[n]和 v[n]中。代码如下:
#include
using namespace std;
int cw=0,bp=0,m,c,i,j,v=0;//cw为当前背包中物品的重量，
int price[1000];//记录物品的价值
int weight[1000];//记录物品的重量
int b[1000];//记录此个排列的状态
int k[1000];//记录最优解时候的排列状态
void Re(int i)
{
if(i>m)
{
if(bp>v)
{
for(j=1;j<=m;j++)
k[j]=b[j];
v=bp;
}
return ;
3.贪心法：
0-1 背包问题与背包问题类似，所不同的是在选择物品
i
1(
i
n
)
装入背包时，可以
选择一部分，而不一定要全部装入背包。这两类问题都具有最优子结构性质，相当相似。但
是背包问题可以用贪心法求解，而 0-1 背包问题却不能用贪心法求解。贪心法之所以得不
到最优解，是由于物品不允许分割，因此，无法保证最终能将背包装满，部分闲置的背包容
量使背包单位重量的价值降低了。事实上，在考虑 0-1 背包问题时，应比较选择物品和不
选择物品所导致的方案，然后做出最优解。由此导出了许多相互重叠的子问题，所以，0-1
背包问题可以用动态规划法得到最优解。在这里就不再用贪心法解 0-1 背包问题了。
4.动态规划法分析：
0-1 背包问题可以看作是寻找一个序列
(
,
xxx
1
3
,
2
,........,
nx
)
，对任一个变量 ix 的判断
是决定 ix =1 还是 ix =0.在判断完 1ix 之后，已经确定了
(
时，会有两种情况：
,
xxx
3
1
,
2
,........,
ix
1
)
，在判断 ix
（1） 背包容量不足以装入物品 i，则 ix =0，背包的价值不增加；
（2） 背包的容量可以装下物品 i，则 ix =1，背包的价值增加 iv 。
这两种情况下背包的总价值的最大者应该是对 ix 判断后的价值。令
iC
),(
j
表示在前
i
1(
i
n
)
个物品中能够装入容量为 j
1(
Wj
)
的背包的物品的总价值，则可以得到如
下的动态规划函数：
iC
)0,(
iC
),(
j
),0(
j
C
(
iC
max{
)1(0
),1
wj
j
i
(
),
,1
(
iCj
iC
,1
wj
i
)
}
wjv
i
i
)2(
式（1）说明：把前面 i 个物品装入容量为 0 的背包和把 0 个物品装入容量为 j 的背包，
得到的价值均为 0.式（2）第一个式子说明：如果第 i 个物品的重量大于背包的容量，则装
入第 i 个物品得到的最大价值和装入第 i-1 个物品得到的最大价值是相同的，即物品 i 不能
装入背包中；第二个式子说明：如果第 i 个物品的重量小于背包的容量，则会有两种情况：
（1）如果把第 i 个物品装入背包，则背包中物品的价值就等于把前 i-1 个物品装入容量为
iwj 的背包中的价值加上第 i 个物品的价值 iv ；（2）如果第 i 个物品没有装入背包，则背
包中物品的价值就是等于把前 i-1 个物品装入容量为 j 的背包中所取得的价值。显然，取二
者中价值较大者作为把前 i 个物品装入容量为 j 的背包中的最优解。
我们可以一步一步的解出我们所需要的解。第一步，只装入第一个物品，确定在各种
情况下背包能得到的最大价值；第二步，只装入前两个物品，确定在各种情况下的背包能
够得到的最大价值；一次类推，到了第 n 步就得到我们所需要的最优解了。最后，
,( WnC
)
便是在容量为 W 的背包中装入 n 个物品时取得的最大价值。为了确定装入背包的具体物
品，从
,( WnC
)
的值向前寻找，如果
,( WnC
)
>
WnC
,1
(
)
,说明第 n 个物品被装入了背包
中，前 n-1 个物品被装入容量为
nwW 的背包中；否则，第 n 个物品没有装入背包中，
前 n-1 个物品被装入容量为 W 的背包中。依此类推，直到确定第一个物品是否被装入背
包为止。由此，我们可以得到如下的函数：
x
i
),(0
(
),1
iC
j
iC
j
,1
),(
j
iCwj
j
i
.
(
iC
),1
j
根据动态规划函数，用一个
(
n
)1
(
W
)1
的二维数组 C 存放中间变量，
iC
][[
j
]
表
示把前 i 个物品装入容量为 j 的背包中获得的最大价值。
设物品的重量存放在数组 w[n]中，价值存放在数组 v[n]中，背包的容量为 W，数组
[
nC
][1
W
]1
存放迭代的结果，数组 x[n]存放装入背包的物品，动态规划解 0-1 背包问
题的源代码如下:
#include
#include
using namespace std;
typedef float T;
//template
void Traceback(int n,T w[],T v[],T p[][2],int *head
{
T j=p[head[0]-1][0],
m=p[head[0]-1][1];
for(int i=1;i<=n;i++)
{
x[i]=0;
for(int k=head[i+1];k<=head[i]-1;k++)
{
if(p[k][0]+w[i]==j && p[k][1]+v[i]==m)
{
x[i]=1;
j=p[k][0];
5.回溯法分析：
用回溯法解 0_1 背包问题时，会用到状态空间树。在搜索状态空间树时，只要其左儿子
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
