第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
空气质量预报模型研究-数学建模.doc
2018 年河北省首届研究生数学建模竞赛
年河北省首届研究生数学建模竞赛
2018
题 目
河北省中南部空气质量预报模型研究
摘
要：
近年来随着我国经济飞速发展，由此产生了一系列生态环境问题，其中大
气污染尤为严重，而作为工业重地的河北省其环境预测防治更是刻不容缓，本
题以此为背景，通过三个为题希望解决关于大气污染预测的问题。其中第一题
要求不同气象因子对污染物的相关性，本文假设各属性之间是相互独立的，因
此使用简单有效的线性回归方法来挖掘各属性对观测值的相关性，通过最小二
乘法计算回归方程的权值，可以发现在不同的城市中，不同季节的不同污染物
受气象因子的影响程度是不同的。根据不同气象因子的权重的绝对值可以得出
相关度（包括正相关和负相关）较高的气象因子，总体上讲降水量和最高气温
对各种污染物的浓度有较大的相关性。第二题本文借鉴了传统的大气点源扩散
衰减模型，进一步构建了叠加的点源扩散模型。本文考虑空气污染物相邻两日
浓度差值的影响因素，其中与风速相关的地表通风系数对污染物传播与扩散有
横向影响，而混合层高度的则对于污染物的扩散有纵向影响，根据不同的静稳
指数，计算石家庄和邢台到其他城市的距离对于污染物扩散的影响，而且污染
物还因为某些物理因素的影响而衰减。本文通过上述影响因子对污染物的扩散
建立了一种合理的可解释的模型，通过最小二乘法进行拟合，求解得到较好的
模型参数。第三题要求对不同季节建立污染物的模型并采用指标对预报结果进
行评价分析，本文使用了改进的 BP 神经网络方法进行模型的构建，并预测未来
几天的值，经过使用相关系数和平均相对误差进行评价分析，得出较好的预测
结果分析值。
关键字：线性回归 扩散衰减模型 BP 神经网络
- 1 -
1 相关性较好的气象因子的选定
1.1 问题摘要
请用适当的方法，挑选出与污染物相关性较好的气象因子，由于各个城市各
季影响因子不同，故不同城市不同季节不同污染物入的气象因子也不同。（以
石家庄和邢台为例分析，数据见附件 1）
分为各个季节-每个季节都有特有的相关性好的气象因子（这些气象因子通
过线性方程得出），最后得出相关性最好的几个因子。
1.2 问题分析
题目要求挑选出与污染物相关性较好的气象因子，通过给出的数据可以
知道，一共有 10 中气象因子，分别是气温 4 次平均℃ ，最高气温℃ ，最低气
温℃，20-20 降水量 mm ，本站气压 4 次平均 hpa ，相对湿度 4 次平均% ，10
分钟风速 4 次平均 m/s ，日最大风风速 m/s ，日照时数合计 h。这十种气象因
子并不是全都是和污染物之间有很好的相关性，可能有一部分根本和污染物之
间没有太大的联系，来着之间不会有太多的相关性，我们挑选出最合适的相关
性的气象因子，来达到模型简化，拟合程度最高的目的。针对某个特定城市，
某个特定污染物，分别找到最适合的反应某个气象因子对于其影响程度的变量。
1.3 问题建模
10 个气象因子气温 4 次平均℃ ，最高气温℃ ，最低气温℃，20-20 降水
量 mm ，本站气压 4 次平均 hpa ，相对湿度 4 次平均% ，10 分钟风速 4 次平均
m/s ， 日 最 大 风 风 速 m/s ， 日 照 时 数 合 计 h 分 别 设 为
X1,X2,X3,X4,X5,X6,X7,X8,X9,X10,每一个气象因子为 X,某一个污染物为 Y，建立拟
合模型[1]，
iYˆ
iXi
(其中 i=1,2,3,4...,10)
然后通过最小二乘法进行拟合，得到相应的 i反应影响大小的一个数。
1.4 分析结果
通过拟合得到不同季节不同城市的不同气象因子的 i，并对数据进行了
一定的处理， 可以得到如下的折线图，通过折线图，可以直观的分析出来各个
城市不同季节不同气象因子对于污染物浓度的影响的大小：
- 2 -
图 1.1
图 1.2
图 1.3
图 1.4
通过图 1.1 可以看出石家庄春季影响因子图可以看出，石家庄春季对于不同
污染物影响较大的是 20-20 降水量这个气象因子和最高气温这个气象因子。
通过图 1.2 石家庄夏季影响因子图可以看出，石家庄夏季对于 PM2.5 来说，
受气温 4 次平均这个气象因子和最低气温这个因子影响较大，对于 O3 来说，受
气温 4 次平均，最高气温，最低气温，20-20 降水量本地气压四次平均气象因
子影响较大。其他污染物来说，受最高气温影响较大。
通过图 1.3 石家庄秋季影响因子图可以看出，石家庄秋季对于各个污染物来
说，受气温 4 次平均，最高气温，最低气温，20-20 降水量影响程度较大。
通过图 1.4 石家庄冬季影响因子图可以看出，石家庄冬季对于各个污染物来
说，受最高气温，20-20 降水量影响程度较大。
图 1.5
图 1.6
- 3 -
图 1.7
图 1.8
通过图 1.5 可以看出邢台春季影响因子图可以看出，邢台春季对于除了 O3
来说，20-20 降水量这个气象因子和最高气温这个气象因子影响程度较大。O3
来说，各个气象因子影响程度不大。
通过图 1.6 可以看出邢台夏季影响因子图可以看出，邢台夏季对于 PM10 来
说，受最高气温这个因子影响较大，对于 O3 来说，受最高气温，最低气温，气
象因子影响较大。对 SO2 来说，收到 20-20 降水量影响程度较大，对其他污染物
来说，相对较缓和，受气象因子的影响较小。
通过图 1.7 可以看出邢台秋季影响因子图可以看出，邢台秋季对于各个污染
物来说，气温 4 次平均，最高气温，最低气温，20-20 降水量影响程度较大。
通过图 1.8 可以看出邢台冬季影响因子图可以看出，邢台冬季对于各个污染
物来说，受 20-20 降水量影响程度较大。
1.5 改进思路
这里我们使用的线性模拟前提假设各个气象因子之间相互是不相关的，
可以在这方面进行一点后期的处理。也可以通过随机森林的方法进行参数的训
练，得到相关值是关于某一气象因子对于污染物的“贡献”。
2 相邻两日浓度差值预测
2.1 问题摘要
采用适当的方法构建空气污染物相邻两日浓度差值的预报模型，对模型的构
建过程进行详细阐述，选取空气污染物对预报模型进行设计。（合理选择城市
分部情况，附件 2 给出其中部分城市的参考数据）
2.2 问题分析：
题目要求求出空气污染物相邻两日浓度差值的预报模型，我们简化考
虑，可以求出前一天的污染物浓度与第二天污染物浓度的关系，通过前一天的
浓度和预测得出的第二天的污染物浓度，就可以得到两者之间的差值。我们在
考虑污染物浓度随着时间的变化时候，同时考虑进去了。
1）不同城市之间污染物浓度的扩散作用
相邻不同城市之间的污染物浓度是会影响到另一个城市的，两者之间存
在扩散作用，往往一个城市的污染物浓度收到另一个城市的浓度扩散的影响。
我们假设一个城市的当天浓度不随其他因素改变，当前的浓度加上相邻城市的
两天之间的扩散浓度就是第二天当前城市的污染物浓度值。
2）风速对于污染物扩散的横向影响
污染物浓度扩散是受到很多因素的影响，这里考虑到风速对于污染物浓
- 4 -
度的扩散的影响，风速越大，污染物浓度扩散的越快，当前城市的污染物浓度
也就越小，相邻城市的污染物浓度增加。
3）混合层高度对于浓度扩散的纵向影响
大气混合层伸展的高度是混合层高度。混合层高度是研究地表向大气排
放污染物状况的重要参数。混合层高度越高，越有利于污染物垂直方向的扩散，
因此，混合层高度是决定地面污染浓度的重要因子。混合层具有明显随时间变
化的特征，不同的气象条件和天气过程会影响混合层高度。例如，起始温度的
垂直结构和地面增温状况会影响混合层高度。混合层是由于温度层结不连续产
生上下层间的湍流不连续而形成。下层空气湍流强，上层空气湍流弱，这就造
成不连续面以下能够发生强烈的湍流混合，使得位温、水汽等要素随高度分布
均匀。由于混合层是湍流受热对流控制的近地面层以上的大气边界层，所以它
也常被称为自由对流层。混合层高度对于污染物的纵向扩散起到很重要的作用。
4）两个城市之间的距离影响
两个城市之间的污染物的扩散当然受到两者之间距离的影响，两个城市
之间的距离越远，扩散到达的时间越长，此城市对另一个城市的影响越小。
综合这几方面的因素，构建适合的污染物浓度模型，得到相对最合适的结果。
2.3 问题建模：
模型假设：
建立污染物的发生和演变规律模型是基于以下假设：1）扩散过程中浓度
在不同方向轴的变化分布是高斯分布；2）污染物扩散服从扩散定律；3）地面
对污染物起全反射作用；4）不考虑泄漏点内部温度的变化对于气体扩散的一影
响；5）物质衰减系数相同；6）假定相邻的城市的污染物浓度在某天范围内不
改变.7）考虑到污染物浓度可能受到的重力，川流扩散，分子扩散，静电力学
和物理学等因素的衰减的影响.
大气点源扩散模式：
采用传统的高斯及法定推荐修正模式：
,(c
),
zyx
Q
2
u
z
y
exp(
2
y
2
2
y
)
{exp(
2
)
(
Hz
e
2
2
s
)
exp(
2
)
)}
(
Hz
e
2
2
s
c 为污染物地面浓度;
Q 为污染物源强（mg/s）;
u 为每天的平均风速（m/s）;
y
为水平方向扩散参数（m）;
z 为铅锤方向扩散参数（m）;
y 为相邻两个城市的距离
H 为混合层高度
这里涉及到了稳定度的划分及扩散参数的计算：
稳定度的划分需要计算太阳倾角、太阳高度角 、太阳辐射等级及大气稳定
和 z 的计算比较困难，往往需要进行特殊的气象观测和大
度等级扩散参数 y
- 5 -
量的计算工作，推荐的计算方法有 P-G 曲线近似式和布里吉斯扩散参数.这里我
们使用第二个布里吉斯扩散参数
稳定度
A B
C
D
E
F
表 2.1 Briggs 城市扩散参数
y
(m)
z (m)
0.32*X/(1+0.0004*X)0.5
0.22*X/(1+0.0004*X)0.5
0.16*X/(1+0.0004*X)0.5
0.11*X/(1+0.0004*X)0.5
0.24*X/(1+0.0001*X)0.5
0.2*X
0.14*X/(1+0.0003*X)0.5
0.8*X/(1+0.00015*X)0.5
模型的叠加及修正简化：
在重力、湍流扩散、分子扩散、静电引力以及其他生物学、 化学和物理
学等因素的作用下， 大气中的颗粒物或某些气体随时会被地表（土壤 、 植物、
水体）或降水滞留或吸收，使这些物质连续不断的从大气向地表作质量转移，
从而减少其在空气中的浓度，为此对各个污染物引入衰减模式[2-3]：
1）源衰减模式[4]：
Q
x
Q
0
{exp[
1
2
)2(
V
d
u
]}
0
x
dx
z
exp(
2
H
2
2
z
)
源衰减模式考虑了大气污染物在扩散稀释过程中连续不断的从大气向 地表
作质量转移，从而减少其在空气中的浓度.
2) 湿沉积修正模式
Q
Qx
0
exp(
/
ux
)
湿沉积修正模式考虑 了 降水对大气污染物源强的影响.
3)化学迁移修正模式
Q
x
Q
0
exp[
/(
cTux
)]
化学迁移修正模式是从化学迁移的 角度对源强衰减提出修正.
4）简化修正模式[4]
Q
Qz
0
exp(
(
xf
))
模型假设各个地区衰减系数相同，所以可以将衰减项进一步简化，即：
此时模型可以表达为：
Q
Qx
0
1
k
C
n
1
k
QA
d
1
k
C
0
其中 C0 表示前一天的污染物浓度，
- 6 -
A
d
1
2
u
z
y
exp(
2
y
2
2
z
)
exp(
2
H
e
2
2
z
)
此模型计算某地区某日污染物浓度时，考虑了存在衰减项的点源前一天浓度。
各个系数 A 可由监测点位置,稳定度以及扩散参数确定，因此无质量只是 Q 与 k，
根据若干组点组成的，通过最小二乘法可以求得 Q 与 k.
2.4 分析结果
我们通过对于不同城市的数据拟合，应用到模型后得到了下列的拟合出的参
数表，并用下列参数进行预测模型的构建。可以通过拟合参数的带入模型进行
相邻两日浓度差值的预测。
表 2.2 不同城市浓度差训练拟合参数表
石家庄
邢台
1/k
Q
1/k
Q
邯郸
廊坊
唐山
0.8871558
-0.15713
0.8872336
0.26255
0.8871913
-100594
0.88719076
0.171891
0.88720655
-0.5051
0.8871904
-0.47084
秦皇岛
0.8872163
0.706048
0.8871753
1.120167
保定
0.887228
-0.61076
0.8872293
-0.67607
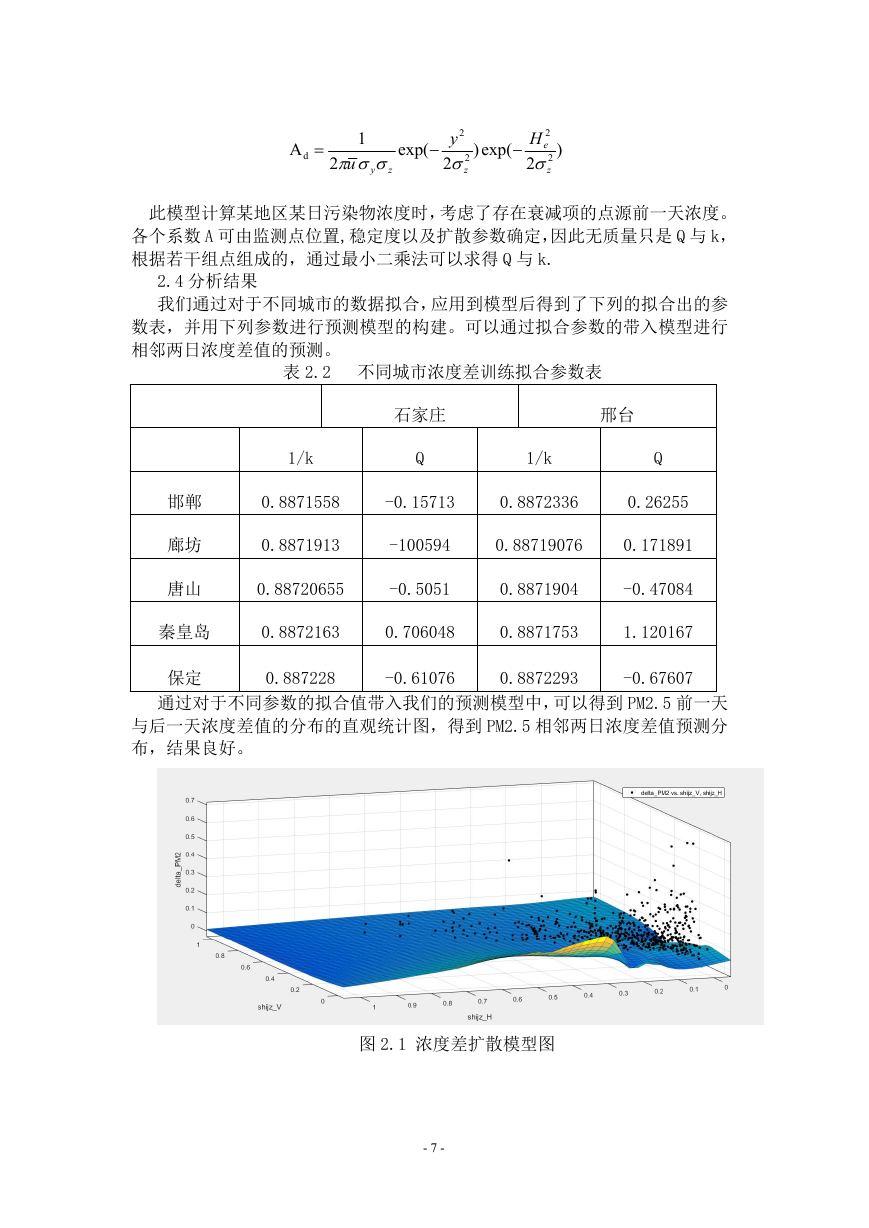
通过对于不同参数的拟合值带入我们的预测模型中，可以得到 PM2.5 前一天
与后一天浓度差值的分布的直观统计图，得到 PM2.5 相邻两日浓度差值预测分
布，结果良好。
图 2.1 浓度差扩散模型图
- 7 -
2.5 改进思路：
这个模型我们仅仅是假设一个城市对于另一个城市的浓度的影响，假设
另一个城市的浓度值是不变化的，不考虑多个城市对于同一个城市的影响以及
此城市对于外界城市浓度的扩散。以后可以考虑到这些方面进行模型的调整优
化。
3 不同季节污染物模型及评价指标
3.1 问题摘要：
利用适当的方法，分不同季节建立的污染物的数学模型，采用不同的指标对
预报结果进行评价分析？
3.2 问题分析：
题目要求分不同的季节建立污染物的数学模型，采用不同的指标对预报结
果进行评价分析，我们这里使用 BP 神经网络进行模型的构建，得到预测结果，
并用相关系数与平均绝对误差进行结果的评估。
空气污染指数(Air pollution index，API)是将常规观测的几种空气污染物
浓度(SO2、NO2 和 PM10 等)简化成为单一的数值形式，具体是将各污染物中污
染分指数最大者取为该区域或城市的 API。API 代表了该城市的污染物污染状况
[5]。
表 3.1 空气污染指数范围以及相应的空气质量级别
空气污染指数 API
空气质量级别
空气质量状况
0-50
51-100
101-200
201-300
>300
I
II
III
IV
V
优
良
轻度污染
中度污染
重度污染
气象因子选取的多少对于 API 有较大影响，同时前几日的气象因子与当日
的 API 具有较强的相关性，故所建模型不仅仅需要考虑当前气象因子，还需要
考虑前几天的气象因子，这样建立的模型具有较强的合理性，也增加了预测的
准确性。
3.3 问题建模
根据 10 个不同的气象因子，作为输入值，输出数据为当天的 API 预测值,
首先因为数据集的不同类型的数据及其量级，量纲存在一定的差异，因此需要
对其进行归一化处理。
BP 网络是由 Rumelhart 和 McCelland 为首的科学家小组于 1986 年提出
的一种按误差逆传播算法训的多层前回馈网络，是目前应用最广泛的神经网络
模型之一[6]。BP 网络包含输入层、隐含层和输出层，该网络的主要特点是信号
前向传递，误差反向传播。在前向传递中，如果输出层得不到期望输出，则转
入反向传播，根据预测误差调整网络权值和阈值，从而使 BP 网络预测输出不
断逼近期望输出。BP 神经网络建立需提供输入值与期望输出值以及各层节点
数、传递函数、训练方法等网络结构参数。现有理论已证明对于任意闭区间上
的任何连续函数都可以用一个隐含层的 BP 神经网络来逼近[7]，因此本文隐含
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
