logo资料库

一种基于压缩感知的轴承故障检测方法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.49M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 一种基于压缩感知的轴承故障检测方法# 张新鹏，胡茑庆，程哲** （国防科学技术大学装备综合保障技术重点实验室，长沙 410073） 摘要：在频域对轴承进行故障检测时，传统的方法需要收集所关心频段的所有数据点然后分 析判断轴承状态，当感兴趣的频段很宽时将增大数据存储压力。针对此问题，本文提出一种 基于压缩感知的轴承故障检测方法，可以在实现故障检测的同时减轻数据存储压力。该方法 首先对所关心频段的数据进行压缩采样，得到相对来说很少的数据点，然后利用匹配追踪算 法找到所关心频段内最大的幅值位置，从而判断轴承的状态。该方法不需要完整地恢复出原 信号，因此不要求原信号是稀疏的，从而扩大了该方法的适用范围。实验结果验证了所提出 方法的有效性。 关键词：机械电子工程；轴承；故障检测；压缩感知；匹配追踪 中图分类号：TH17 TP306 A Bearing Fault Detection Method base on Compressed Sensing (Science and Technology on Integrated Logistics Support Laboratory, National University of ZHANG Xinpeng, HU Niaoqing, CHENG Zhe Defense Technology, ChangSha 410073) 5 10 15 20 25 30 Abstract: For bearing fault detection in frequency domain, traditional methods estimate bearing fault condition based on the whole data points of interesting frequency range, which will burden the storage when interested frequency range is extremely wide. A new bearing fault detection method based on compressed sensing will be proposed in this paper in allusion to the problem mentioned above, which can achieve fault detection and also alleviate the storage burden of mass data. The method presented here carried out compressive sampling first to interested range in frequency domain and few data points relatively will be acquired. Then the position corresponding to the maximum amplitude will be located using the few data points based on matching pursuit and the bearing condition will be estimated finally. Sparsity of original signal is not demanded since the signal does not need to be recovered completely, which will also helped to expanded the method to other signals with similar characteristics in frequency domain. Related test will be achieved to verify the effectiveness of the method proposed in this paper. Keywords: Mechatronic Engineering; Bearing; Fault Detection; Compressed Sensing; Matching Pursuit 35 0 引言 轴承是机械设备中最常用也是最易损坏的零件之一，除转速高、负荷大外，工况也极端 恶劣，属故障多发件。轴承故障引起的振动特征表现为在振动信号中存在着冲击脉冲[1]。在 时域中，冲击使信号的均值、方差等发生变化；而在频域中，冲击使得信号高频成分明显增 多，信号能量分布将发生变化。因此，可以通过分析能量的频域分布来对轴承状态进行判断， 这也是目前应用较多的方法。 40 就轴承故障检测而言，一种比较简单的策略是对监测到的振动信号做频谱分析，得到信 号的频域能量分布，对比当前状态能量分布与已知的正常状态能量分布，如果当前状态频谱 大幅偏离正常状态，则判断轴承状态出现异常。如图 1 所示为 6205-2RS JEK SKF 深沟球轴 基金项目：高等学校博士学科点专项科研基金(20114307110017) 作者简介：张新鹏，(1986-)，男，博士研究生，主要研究方向：状态监控与故障诊断。 通信联系人：胡茑庆，（1967-），男，教授，主要研究方向：状态监控与故障诊断，装备综合保障。E-mail: hnq@nudt.edu.cn - 1 -
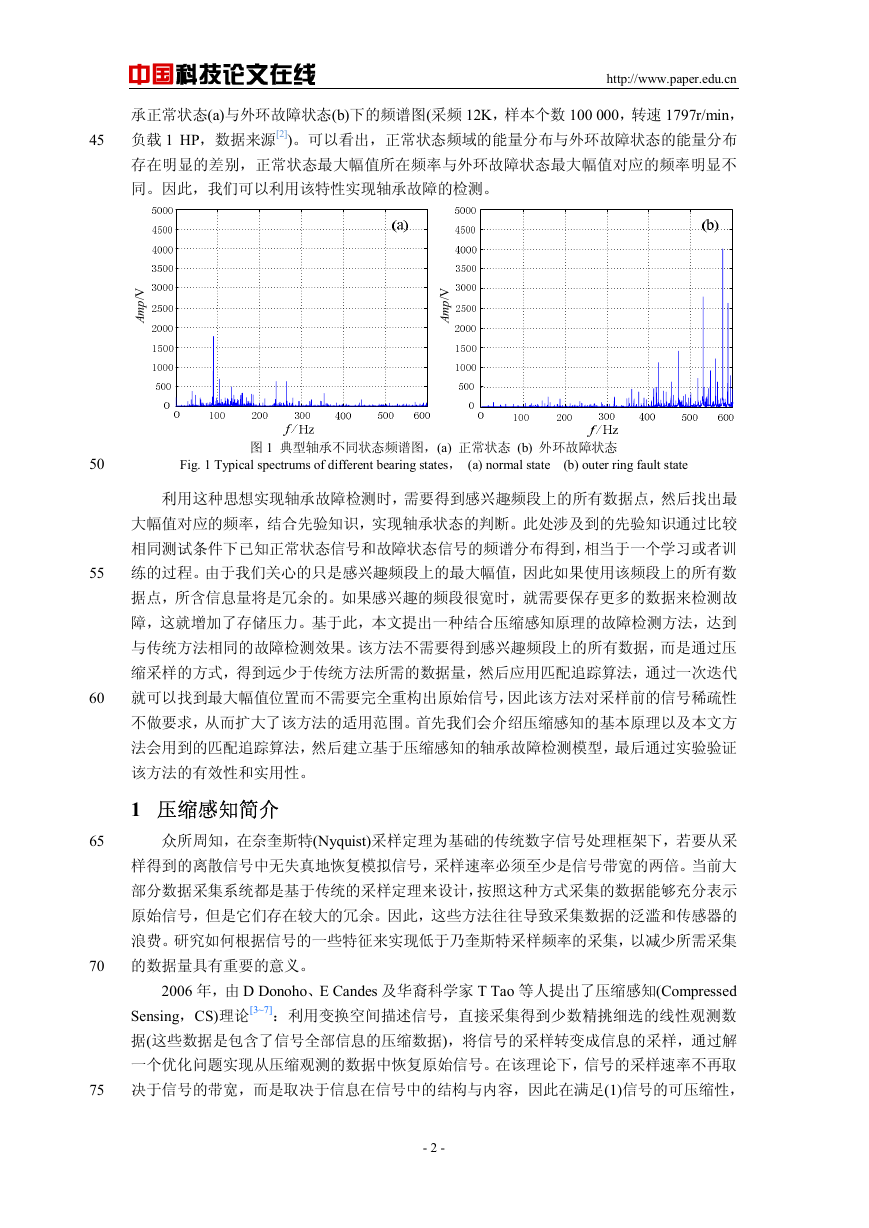
    中国科技论文在线 http://www.paper.edu.cn 45 承正常状态(a)与外环故障状态(b)下的频谱图(采频 12K，样本个数 100 000，转速 1797r/min， 负载 1 HP，数据来源[2])。可以看出，正常状态频域的能量分布与外环故障状态的能量分布 存在明显的差别，正常状态最大幅值所在频率与外环故障状态最大幅值对应的频率明显不 同。因此，我们可以利用该特性实现轴承故障的检测。 V / p m A V / p m A 50 55 60 图 1 典型轴承不同状态频谱图，(a) 正常状态 (b) 外环故障状态 Fig. 1 Typical spectrums of different bearing states， (a) normal state (b) outer ring fault state 利用这种思想实现轴承故障检测时，需要得到感兴趣频段上的所有数据点，然后找出最 大幅值对应的频率，结合先验知识，实现轴承状态的判断。此处涉及到的先验知识通过比较 相同测试条件下已知正常状态信号和故障状态信号的频谱分布得到，相当于一个学习或者训 练的过程。由于我们关心的只是感兴趣频段上的最大幅值，因此如果使用该频段上的所有数 据点，所含信息量将是冗余的。如果感兴趣的频段很宽时，就需要保存更多的数据来检测故 障，这就增加了存储压力。基于此，本文提出一种结合压缩感知原理的故障检测方法，达到 与传统方法相同的故障检测效果。该方法不需要得到感兴趣频段上的所有数据，而是通过压 缩采样的方式，得到远少于传统方法所需的数据量，然后应用匹配追踪算法，通过一次迭代 就可以找到最大幅值位置而不需要完全重构出原始信号，因此该方法对采样前的信号稀疏性 不做要求，从而扩大了该方法的适用范围。首先我们会介绍压缩感知的基本原理以及本文方 法会用到的匹配追踪算法，然后建立基于压缩感知的轴承故障检测模型，最后通过实验验证 该方法的有效性和实用性。 1 压缩感知简介 65 众所周知，在奈奎斯特(Nyquist)采样定理为基础的传统数字信号处理框架下，若要从采 样得到的离散信号中无失真地恢复模拟信号，采样速率必须至少是信号带宽的两倍。当前大 部分数据采集系统都是基于传统的采样定理来设计，按照这种方式采集的数据能够充分表示 原始信号，但是它们存在较大的冗余。因此，这些方法往往导致采集数据的泛滥和传感器的 浪费。研究如何根据信号的一些特征来实现低于乃奎斯特采样频率的采集，以减少所需采集 的数据量具有重要的意义。 70 2006 年，由 D Donoho、E Candes 及华裔科学家 T Tao 等人提出了压缩感知(Compressed Sensing，CS)理论[3~7]：利用变换空间描述信号，直接采集得到少数精挑细选的线性观测数 据(这些数据是包含了信号全部信息的压缩数据)，将信号的采样转变成信息的采样，通过解 一个优化问题实现从压缩观测的数据中恢复原始信号。在该理论下，信号的采样速率不再取 决于信号的带宽，而是取决于信息在信号中的结构与内容，因此在满足(1)信号的可压缩性， 75 - 2 -
    中国科技论文在线 http://www.paper.edu.cn (2)表示系统与观测系统的不相关性两大条件下，从低分辨观测中恢复高分辨信号就成为了 可能[8]。CS 理论避开了高速采样，意味着信号的采样与处理都可以以非常低的速率进行， 这将显著降低数据存储和传输代价，以及信号处理时间和计算成本，给信号处理领域带来新 的冲击。另一方面，这种压缩观测的思想也给高维数据分析指出了一条新的途径。压缩感知 的基本数学模型如下： 80 若将 N 维实信号 x R ×∈ 1N 在某组正交基 iψ i 1 { }N iψ = ( 为 N 维列向量)下进行展开，即： = ∑ (2.1) θψ i N i x I 1 = 其中展开系数 T θ ψ ψ i = = x , i i x ，也就是说，用一组正交基的组合来表示信号 x，写 成矩阵的形式，可以得到： × 1 2 , ] R ∈ θ N N ,..., ,..., Ψ = [ ψ ψ ψ N ，为正交基字典矩阵（满足 T x = Ψ (2.2) ΨΨ = Ψ Ψ = ），展开系数 这里 , θ=[ θ θ θ 。假设系数向量θ 是 K 稀疏的，也就是说其中非零系数的个数为 K＜＜N。 那么采用另一个与正交基字典 Ψ 不相关的观测矩阵Φ ：M×N（M＜＜N）（这里Φ 的每一 行可以看作是一个传感器，它与信号相乘，获取了信号的部分信息），对信号 x 执行一个压 缩观测： ]T I N 1 2 T 就可以得到 M 个线性观测（或投影） x 的足够信息，如图 2 所示。 y x= Φ (2.3) y R∈ ，这些少量线性投影中则包含了重构信号 M 图 2 压缩观测向量的矩阵表示 Fig. 2 Matrix representation of compressed observation vector 从 y 中恢复 x 是一个解线性方程组的问题，但从方程(2.3)上看，这似乎是不可能的，因 为这是一个未知数个数大于方程个数的病态方程，存在无穷多个解。但是，将式(2.2)带入式 (2.3)，记 CS 信息算子 CSA = ΦΨ ，可以得到： = ΦΨ (2.4) 虽然从 y 中恢复θ 也是一个病态问题，但是因为系数θ 是稀疏的，这样未知数个数将大大减 少，使得信号重构称为可能。 A θCS θ= y 85 90 95 100 105 因此，在满足信号稀疏性以及字典矩阵 Ψ 与观测矩阵Φ 不相关的前提下，通过求解一 个非线性优化问题就能从观测 y、观测矩阵Φ 和字典矩阵 Ψ 中近乎完美的重建信号 x。信号 - 3 -
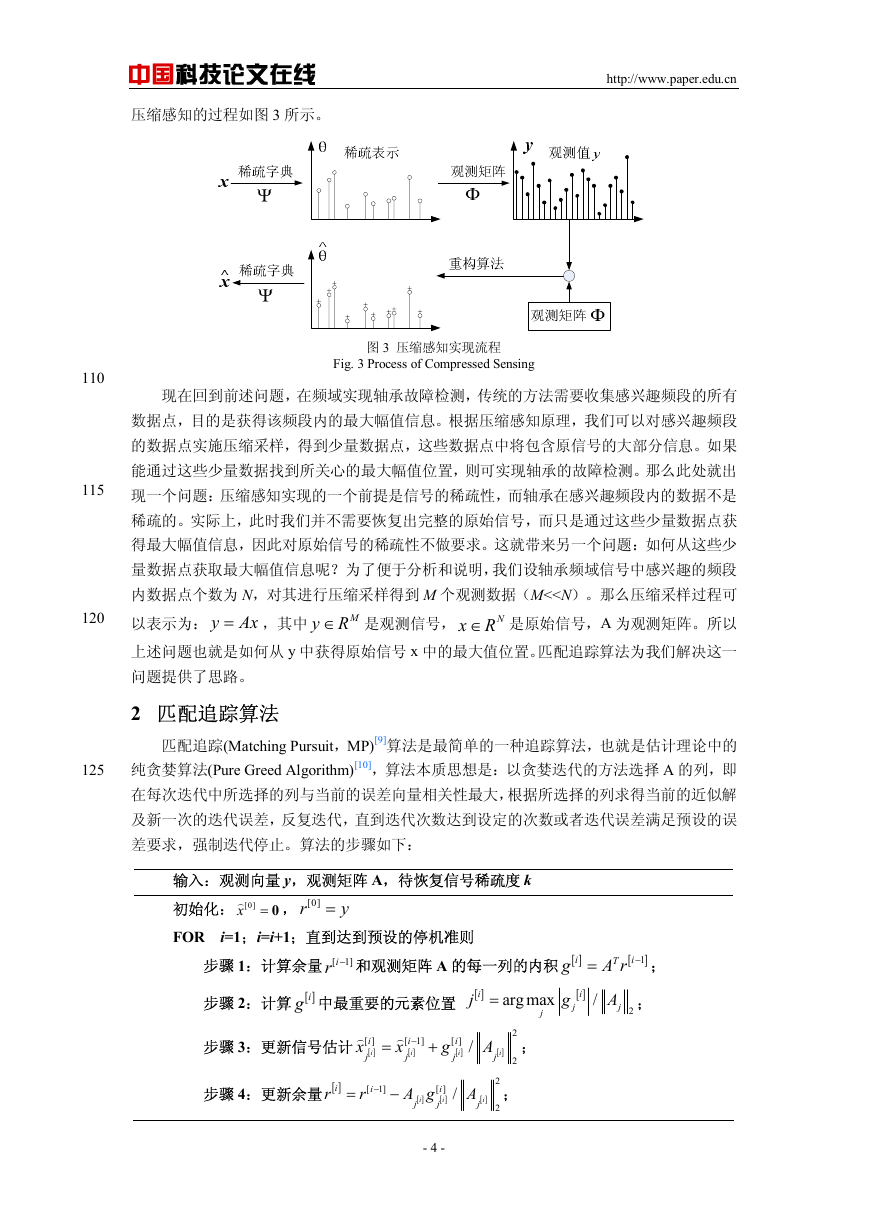
    中国科技论文在线 压缩感知的过程如图 3 所示。 http://www.paper.edu.cn 110 115 120 图 3 压缩感知实现流程 Fig. 3 Process of Compressed Sensing 现在回到前述问题，在频域实现轴承故障检测，传统的方法需要收集感兴趣频段的所有 数据点，目的是获得该频段内的最大幅值信息。根据压缩感知原理，我们可以对感兴趣频段 的数据点实施压缩采样，得到少量数据点，这些数据点中将包含原信号的大部分信息。如果 能通过这些少量数据找到所关心的最大幅值位置，则可实现轴承的故障检测。那么此处就出 现一个问题：压缩感知实现的一个前提是信号的稀疏性，而轴承在感兴趣频段内的数据不是 稀疏的。实际上，此时我们并不需要恢复出完整的原始信号，而只是通过这些少量数据点获 得最大幅值信息，因此对原始信号的稀疏性不做要求。这就带来另一个问题：如何从这些少 量数据点获取最大幅值信息呢？为了便于分析和说明，我们设轴承频域信号中感兴趣的频段 内数据点个数为 N，对其进行压缩采样得到 M 个观测数据（M<
    中国科技论文在线 http://www.paper.edu.cn [ ]ix) END FOR 输出：误差向量 [ ]ir ，x 的稀疏逼近 从几何的角度来分析，MP 算法首先计算余量到每个原子（也就是 A 的每一列）的投影， 然后找到投影长度最大时对应的那个原子，设这个原子为第 j 列，该原子就是与余量 r 最匹 iA = 配的。如果我们令每个原子的 2 范数等于单位长度，即令 2 1 ，(i=1，2，…，n)，此时 余量在第 j 个原子上的投影长度，就等于 x 中第 j 个位置上的非零元素绝对值。即有以下结 论： 如果 则有 T A j ⋅ y / A j = max { n 1,2, = , L i 2 T A y i ⋅ / A i }, 2 j ∈ {1,2, n , } L (3.1) x j = max { n 1,2, = , L i x i } (3.2) T A j ⋅ iA = ，所以(3.1)可变为 上述结论很容易证明：由于 2 1 max { {1,2, = n 1,2, = ) A y A ⋅ i i A i (3.3)就可以得到式(3.2)，结论得证。 又根据 x 的定义，我们有 A y ⋅ i y ( }, ∈ x i = , L / 2 j i T 2 ，因为 2 1 iA = ，所以 x i = T A y i ⋅ ，将其带入 T n , } L (3.3) 因此第一次迭代找出的位置就是 x 中最大元素所在位置。我们使用 MP 算法，选择合适 的观测矩阵 A，设定 x 稀疏度 k=1，应用 MP 算法执行一次迭代操作，就能得到 x 中的最大 元素所在位置，而对于其他位置，由于我们设定 x 的稀疏度为 1，所以此时算法将默认除了 最大元素位置外的其他位置元素值一律为零。虽然此时将无法重构出原始信号 x，但是我们 最初的目的不是为了重构 x，而仅仅是找到 x 中最大的元素所在位置。这样就得到了一种从 y 中直接判断轴承状态的方法，即设原信号 x 的稀疏度 k=1，然后应用 MP 算法，执行一次 迭代操作，找到 x 中最大元素对应的位置，根据该位置信息结合先验知识就可以判断轴承是 否发生故障。下面我们将基于 MP 算法建立轴承故障检测模型，并通过实验数据来验证该检 测模型的有效性。 3 实验验证 通过前述分析我们可以建立基于压缩感知的轴承故障检测模型，如图 4 所示。根据上述 模型，相应的轴承故障检测步骤如下： 步骤 1：对时域信号进行预处理，然后计算相应的频域信号； 步骤 2：根据轴承参数和转速，选择感兴趣的频段； 步骤 3：设计观测矩阵； 步骤 4：对感兴趣频段内的数据实施压缩采样，得到观测向量； 步骤 5：应用匹配追踪算法找出最大幅值对应的频率； 步骤 6：根据最大幅值位置来判断轴承状态，即：当最大幅值位置大幅偏离正常状态频 域最大能量对应频率附近时，判断轴承出现故障；否则，判断轴承处于正常状态。 - 5 - 130 135 140 145 150 155
    中国科技论文在线 http://www.paper.edu.cn 实验中采集 6205-2RS JEK SKF 深沟球轴 承不同状态的振动数据(数据来源[2])，采样期 间轴承转速为 1797r/min，信号的采样频率为 12K，负载为 1 HP。测试数据由 960 个样本组 成，包括正常状态样本 480 个，故障状态样本 480 个，每个样本包含 10 000 个数据点。由轴 承转速和轴承参数分析可知，在 0-600Hz 范围 内，轴承在不同状态下对应的最大幅值所在频 率不同，具体来说，正常状态最大幅值出现在 频率 88.8Hz 左右；内环故障时最大幅值出现 在 454.8Hz 左右；外环故障时最大幅值出现在 536.4Hz 左右。根据上述先验知识，我们重点 关注频率范围为 0-600Hz 的频段，由于采样频 率为 12K，因此该频段共有 500 个数据点。如 果轴承状态是正常的，那么在这一频段中，最 大幅值应出现在 88.8Hz 附近；同样地，如果 轴承发生故障，不论是内环故障还是外环故 障，最大幅值的位置都应大幅偏离 88.8Hz。 据此我们可以根据该频段的最大幅值位置信息来判断轴承所处的状态。在实验中为了防止波 形小范围的波动对结果的影响，如果最大幅值出现在 88.8±10Hz 的范围内，我们便认为对应 的状态为正常状态。实验中使用高斯随机观测矩阵[11][12]，由于算法设定稀疏度为 k=1，根据 观测数据量的选择原则[7][13]，压缩感知采样点数取 50 点，即观测矩阵维数为 50×500。 图 4 基于压缩感知的轴承故障检测模型 Fig. 4 Bearing fault detection model based on compressed sensing 160 165 170 175 180 考察所提方法的故障检测性能。根据前述步骤建立基于匹配追踪的故障检测模型，对 960 个样本进行故障检测。为减轻由于观测矩阵的随机性所造成的检测结果不稳定现象，实 验中对检测过程重复 1000 次，取平均值得到最终故障检测结果。检测结果如表 1 所示。 方法 传统方法 轴承状态 正常状态 故障状态 正常状态 故障状态 表 1 故障检测结果 Tab. 1 Fault detection result 样本个数 检出个数 480 480 480 480 480 480 480 480 检出率 100% 100% 100% 100% 185 190 195 本文方法 上述结果表明，本文所提方法可以有效地实现轴承故障的检测。使用传统方法实现轴承 故障检测需要至少 500 个频域数据点来分析，而本文方法仅需要 50 个数据点就能够得到与 传统方法相同精度的故障检测率，这对于缓解因数据量过大所造成的存储压力具有重要意 义。需要指出的是，由于上述检测方法仅使用了原始信号的部分信息，所以对于相同的样本， 该方法的故障检测率上限为传统方法的故障检测率。 4 结论 本文根据轴承正常状态和故障状态下频谱能量分布不同的特点，提出了一种基于压缩采 样和 MP 重构算法的轴承故障检测方法，实验结果表明所提方法能够在保证检测效果的同时 大幅减少所需的样本数。在压缩采样过程中，本文使用了高斯随机观测矩阵，同时观测数据 取的是 50 点。实际上，观测矩阵也可以取其他的矩阵如贝努力随机矩阵等，而观测数据取 - 6 -
    中国科技论文在线 http://www.paper.edu.cn 50 点是有冗余的，下一步研究工作将改变观测矩阵类型以及观测数据量，研究不同情况下 算法的故障检测性能。文中方法仅用最大幅值信息来检测故障，因为实验中所用轴承故障特 征较为明显，所以检测率较高，而在故障特征不明显的情况下可能会得到不稳定的结果，因 此下一步的研究将尝试使用若干个较大的幅值信息来完成故障的检测。同时，本文所提方法 是基于不同状态下频谱能量分布不同这一前提而提出来的，考虑到该方法的进一步应用，对 振动信号不同稀疏表示域的研究也是未来工作的一个方向。 [参考文献] (References) [1] 梅宏斌．滚动轴承振动监测与诊断理论方法系统[M]．北京：机械工业出版社，1995． [2] http://www.eecs.case.edu/laboratory/bearing/fault_specs.htm. [3] D DONOHO. Compressed sensing [J]. IEEE Transactions on Information Theory，2006，52(4)：1289-1306. [4] E CANDES，M WAKIN. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine， 2008，25(2)：21-30. [5] D DONOHO，Y TSAIG. Extensions of compressed sensing [J].Signal Processing，2006，86(3)：533-548. [6] E CANDES，J ROMBERG，T TAO. Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory，2006，52(2)：489-509. [7] E CANDES，T TAO. Near optimal signal recovery from random projections：Universal encoding strategies [J]. IEEE Transactions on Information Theory，2006，52(12)：5406- 5425. [8] 焦李成，杨淑媛，刘芳，侯彪.压缩感知回顾与展望[J]. 电子学报, 2011, 39(7):1652-1654. [9] S. MALLAT，Z. ZHANG. Matching Pursuit with time-frequency dictionaries[J] .IEEE Transactions on Signal Processing，1993，41(12)：3397-3415. [10] J. H .FRIEDMAN, J. W. TUKEY. A projection pursuit algorithm for exploratory data analysis[J]. IEEE Trans Comput,1974,23(9)：881-890,. [11] DUARTEM, DAVENPORT M, WAK N M, et al. Sparse signal detection from incoherent projection[A]. IEEE Int. Conf on Acoustics, Speech, and Signal Processing (ICASSP)[C], Toulouse, France, May 2006. 305-308. [12] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transaction on Information Theory，2007，53(12)：4655-4666. [13] RICHARD BARANIUK，MARK DAVEPORT，RONALD DEVORE，et al．A simple proof of the restricted isometry property for random matrices[J].Constructive Approximation，2007，23(4-6)：918-925． 200 205 210 215 220 225 - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料