logo资料库

物质中带有无菌中微子的振荡的紧凑摄动表达式.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：1.16M 资料格式：pdf 举报 版权申诉
第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
资料共14页，剩余部分请下载后查看
    PHYSICAL REVIEW D 101, 056005 (2020) Compact perturbative expressions for oscillations with sterile neutrinos in matter Theoretical Physics Department, Fermi National Accelerator Laboratory, Batavia, Illinois 60510, USA Stephen J. Parke * Xining Zhang † Enrico Fermi Institute and Department of Physics, University of Chicago, Chicago, Illinois 60637, USA (Received 28 May 2019; accepted 2 January 2020; published 5 March 2020) We extend a simple and compact method for calculating the three-flavor neutrino oscillation probabilities in uniform matter density to schemes with sterile neutrinos, with favorable features inherited. The only constraint of the extended method is that the scale of the matter potential is not significantly larger than the atmospheric Δm2, which is satisfied by all the running and proposed accelerator oscillation experiments. Degeneracies of the zeroth order eigensystem around solar and atmospheric resonances are resolved. Corrections to the zeroth order results are restricted to no larger than the ratio of the solar to the atmospheric Δm2. The zeroth order expressions are exact in vacuum because all the higher order corrections vanish when the matter potential equals zero. Also, because all the corrections are continuous functions of matter potential, the zeroth order precision is much better than Δm2⊙=Δm2 atm for the weak matter effect. Numerical tests are presented to verify the theoretical predictions of the exceptional features. Precision and speed comparisons with previous 3 þ 1 methods are performed. Moreover, possible applications of the method in experiments to check the existence of sterile neutrinos are discussed. DOI: 10.1103/PhysRevD.101.056005 I. INTRODUCTION Since the discovery of neutrino oscillations, [1], which determined that neutrinos are massive particles, many studies of neutrino scenarios beyond the three-flavor Standard Model have been performed. One promising solution to the origin of the neutrino masses is a theoretical scheme with additional sterile neutrinos. In such a scheme, neutrino oscillations will be modified because of the additional mixing with sterile neutrinos. In matter, calculations of neutrino propagation will be significantly more complicated since the sterile neutrinos also change the Wolfenstein matter effect term [2] in the Hamiltonian. There have been some analytical derivations of the matter effect in a 3 þ 1 scenario, i.e., one sterile neutrino [3] in addition to the three active ones. However, the exact analytical solutions are impos- sible for more than one sterile neutrino because a quintic *parke@fnal.gov; † xining@uchicago.edu; Published by the American Physical Society under the terms of the Creative Commons Attribution 4.0 International license. Further distribution of this work must maintain attribution to the author(s) and the published article’s title, journal citation, and DOI. Funded by SCOAP3. or even higher order equation will be encountered. Consequently, alternative perturbation approaches should be considered. A satisfying perturbative framework, regardless of the existence of sterile neutrinos, is expected to possess the following properties: the expansion parameter is small, crossings of zeroth order eigenvalues are avoided any- where, and the approximated values go to the exact ones in vacuum. Recently, a compact perturbative framework achieving all the objectives above was developed by Denton, Minakata, and Parke (DMP) to calculate the propagation of neutrinos in matter under the assumption of the standard three-flavor scheme [4–6]. The main focus in this paper is to extend the principle and method of the DMP framework to schemes with sterile neutrinos when the scale of matter potential a is smaller than or comparable to Δm2 atm, which is the case of all running and proposed accelerator neutrino oscillation experiments. The expansion parameter [5,7,8], which will be retained by the extension, is Δm2 ð1Þ The perturbative Hamiltonian will have no diagonal ele- ments, and all its off-diagonal elements are proportional to ϵ ≡ Δm2 21=Δm2 ee ≡ cos2 θ12Δm2 ee ≃ 0.03; 31 þ sin2 θ12Δm2 32: 2470-0010=2020=101(5)=056005(14) 056005-1 Published by the American Physical Society
    STEPHEN J. PARKE and XINING ZHANG PHYS. REV. D 101, 056005 (2020) ϵ and vanish in vacuum. Crossings of the zeroth order active eigenvalues will be resolved by a series of real or complex rotations, whereas crossings of the large sterile eigenvalues will not be considered since this will happen only if the matter effect is extremely large. The structure of this paper is listed as follows. In Sec. II, we derive details of the rotations. This gives the zeroth order Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix and eigenvalues. The perturbative Hamiltonian is also deter- mined by the rotations. In Sec. III, we discuss the higher order corrections by perturbative expansions after the rotations. A numerical test will also be presented to verify the predicted precision. In Sec. IV, we use these perturbative expressions to calculate the oscillation probabilities of different channels and baselines. Moreover, potential appli- cations of the method are discussed. We compare our method to some former works in Sec. V. Section VI is the conclusion. All other remarks and supplementary materials that are useful can be found in the Appendixes. II. ROTATIONS TO DERIVE ZEROTH ORDER APPROXIMATIONS AND PERTURBATIVE HAMILTONIAN The principle of the method in Refs. [4–6] is that by implementing a series of rotations of the Hamiltonian, one can disentangle the crossings of the diagonal elements and diminish the off-diagonal elements to arbitrary scales. In particular: (1) In the given Hamiltonian in the flavor basis, find the sector with leading order (largest absolute value) off-diagonal element; then, perform a rotation to diagonalize this sector. (2) Use the rotated Hamiltonian to replace the initial one, and repeat the process until all the off-diagonal elements are smaller than the expected scale and the diagonal element crossings are eliminated. In principle, the above process is not designated to any specific dynamical system and is also applicable to the schemes with sterile neutrinos. However, this scheme must be implemented with con- siderable care; otherwise, the resulting analytic expressions become extremely long and complicated. First, one has to carefully choose the extension to the PMNS matrix to include sterile neutrinos as the standard choice here is far from optimal. Second, one has to decide whether or not one deals with all level crossings of the diagonal elements of the Hamiltonian or restrict the range of applicability of the result. We address these issues in depth in the following subsections. A. PMNS matrix in vacuum If we assume a 3 þ N scheme, i.e., there are N sterile neutrinos in the scheme, the Hamiltonian in the flavor basis will be H ¼ 1 2E½UPMNSdiagð0; Δm2 × U† PMNS þ diagðaðxÞ; 0; 0; bðxÞ; …; bðxÞފ. ð2Þ 21; Δm2 31; Δm2 41; …; Δm2 N1Þ UPMNS is the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) unitary matrix, [9,10], which relates the mass eigenstates to flavor eigenstates, i.e., Yeρ  E GeV   GFNnE: jνiflavor ¼ UPMNSjνimass: ð3Þ ffiffiffi The Wolfenstein’s matter potentials, a and b are given by [2]: p ffiffiffi a ¼ 2 GFNeE ≃ 1.52 × 10−4 eV2; 2 p ð4Þ b ¼ 2 For Earth matter, the neutron number density Nn is approx- to the electron number density Ne so imately equal that b ≈ a=2. g · cm−3 The PMNS matrix UPMNS in vacuum, which relates the flavor basis and the mass basis, is the product of a series of (complex) rotations [9,10]. In the Standard Model, the ≡ U23U13U12. In the convention is chosen to be USM 3 þ N scheme, there will be extra rotations mixing with sterile neutrinos. It is natural to require that the convention is equivalent to that of the 3νSM, i.e., three-flavor case of the Standard Model, if all the extra rotations are trivial. Therefore, we will keep the relative positions of the three rotation matrices in the active sector when defining the PMNS matrix with sterile neutrinos. PMNS Also, it is observed that both the second and the third rows vanish in the matter potential term in Eq. (2); thus, we will keep U23 as the first rotation in the PMNS matrix so the rhs of Eq. (2) will be independent of the 2–3 mixing parameters if we perform the U23 rotation. The last step to determine the convention of the PMNS matrix is finding places after the U23 for the rotations mixing with the sterile neutrinos. By trying different choices to simplify the calculation processes, we adopt the following convention of the PMNS matrix, UPMNS ≡ U23ðθ23; δ23ÞUsterileU13ðθ13ÞU12ðθ12Þ; ð5Þ where Usterile is the product of all the rotations mixing with sterile neutrinos. This choice leads to significant reductions in the complexity of the calculations and the resulting expressions. Physics, of course, is independent of this choice. In the following sections, we will use the 3 þ 1 scheme as an example to develop the expressions for the schemes with sterile neutrinos. In particular, we choose1 1The convention of the CP phases is chosen to simplify the calculation process. Different conventions can be related by pure phase transformations. 056005-2
    COMPACT PERTURBATIVE EXPRESSIONS FOR … PHYS. REV. D 101, 056005 (2020) U3þ1 sterile ≡ U34ðθ34; δ34ÞU24ðθ24; δ24ÞU14ðθ14Þ: ð6Þ ffiffiffi Current global fits [11–13] suggest jUi4j ∼ 0.1, so in this ffiffiffi ϵp Þ, which means ϵp Þ for i ¼ 1, 2, 3. The small parameter ϵ is paper, we assume that Usterile ≃ 1 þ Oð that si4 ∼ Oð defined in Eq. (1). The convention in Eq. (5) is different from the usual one used by many papers in which Usterile comes before (i.e., on the left side of) all three rotations in the active sector (see, e.g., Ref. [14]). We will derive the relations of the mixing angles and phases connecting both conventions in Appendix A. where jνif Hamiltonian becomes is the flavor basis. After the rotations, ˜H ≡ U†  ˜H sterile ¼  23ðθ23; δ23ÞHU23ðθ23; δ23ÞUsterile U† þ ˜HM: M2 2E the ð8Þ In the above equation M2ðbÞ ≡ Δm2 34, ˜H is a 3 × 3 submatrix in the active sector, and in ˜HM, all the elements not in the fourth column or row vanish. Based on the scales, we can distribute the elements of ˜H 41 þ bc2 14c2 24c2 ð9Þ ð10Þ 1 CA; B. U23 and Usterile rotations We first define a rotated basis j˜νi by j˜νi ≡ U† ¼ U† 23jνif U† 14ðθ14ÞU† sterile 24ðθ24; δ24ÞU† 34ðθ34; δ34ÞU† 0 B@ ˜H0 ¼ 1 2E into two parts, i.e., ˜H ¼ ˜H0 þ ˜H1: The leading order term is 23ðθ23; δ23Þjνif; ð7Þ λa s13c13Δm2 ee þ ϵbk13c24c34e−iδ34 s13c13Δm2 ee þ ϵbk13c24c34eiδ34 λb λc where kij ≡ si4sj4 ϵ ∼ Oð1Þ; i; j ∈ f1; 2; 3g; ð11Þ and the diagonal elements, which can be approximations to the eigenvalues, are λa ¼ ðs2 λb ¼ ϵðc2 λc ¼ ðc2 13 þ ϵs2 12Δm2 13 þ ϵs2 ee þ ac2 34Þ; 12ÞΔm2 ee þ bk22c2 12ÞΔm2 ee þ ϵbk33: 14 þ ϵbk11c2 24c2 34; ð12Þ In the first order term ˜H1, all the diagonal elements vanish, and the off-diagonal elements are ð ˜H1Þ12 ¼ ϵ ð ˜H1Þ23 ¼ ϵ ð ˜H1Þ13 ¼ 0: 2Eðc12s12c13Δm2 2E½−c12s12s13Δm2 34e−iδ34Þ; ee þ bk12c24c2 ee þ bk23c34eiðδ24−δ34ފ; ð13Þ 34Þc14s14; 24c2 2Eða þ bc2 c14c24s24c2 34eiδ24; c14c24c34s34eiδ34: ð ˜HMÞ14 ¼ − 1 ð ˜HMÞ24 ¼ − b 2E ð ˜HMÞ34 ¼ − b 2E ð ˜HMÞ44 ¼ 0: ffiffiffi ϵp Þ, it is easy to see that ð14Þ ffiffiffi ϵp Þ. Since si4 ∼ Oð ˜HM ∼ Oð Although ˜HM is not as small as OðϵÞ, it will be a part of the ffiffiffi ϵp Þ. The perturbative Hamiltonian. However, this does not mean that the first order corrections must be as large as Oð mass of the heavy sterile neutrino will be an alternative parameter which controls scales of the correction terms. More specifically, in a perturbative expression, all nonzero ˜HM are divided by M2. For large M2, the elements of quotient gives a small term in the perturbation expansion. ˜HM being a Another condition that perturbative Hamiltonian is that it consists of terms propor- tional to a and b, which means that it vanishes in vacuum. This is crucial because we require the perturbative ex- pressions to be exact in vacuum. is necessary for Nonzero elements of ˜HM are listed below (the Hamiltonian is a Hermitian matrix) C. U13 rotation Now, the dominating off-diagonal term (except the ones in ˜HM) comes from the (1-3) sector of ˜H0. Because of the 056005-3
    STEPHEN J. PARKE and XINING ZHANG PHYS. REV. D 101, 056005 (2020) complex phase δ34, the rotation will not be real. Let us assume that the rotation is U13ð˜θ13; α13Þ, where ˜θ13 is the 2 is the complex phase. After this real rotation angle and α13 rotation, the neutrino basis becomes cos 2˜θ13 ¼ λc − λa λþ − λ− ; α13 ¼ Arg½s13c13Δm2 ee þ ϵbk13c24c34e−iδ34Š: ð22Þ ˆH1 are The elements of ð ˆH1Þ12 ¼ ϵ ee 34 ˜c13 − k23c34 ˜s13eiðδ34þα13ފe−iδ24g; 2Efc12s12ðc13 ˜c13 þ s13 ˜s13e−iα13ÞΔm2 þ b½k12c24c2 2Efc12s12ð−s13 ˜c13 þ c13 ˜s13eiα13ÞΔm2 þ bðk12c24c2 34 ˜s13eiα13 þ k23c34 ˜c13e−iδ34Þeiδ24g; ee ð23Þ ð ˆH1Þ23 ¼ ϵ ð ˆH1Þ13 ¼ 0: The Hamiltonian in the sterile sector becomes 13ð˜θ13; α13Þ ˜HMU13ð˜θ13; α13Þ: ˆHM ≡ U† ð24Þ ð17Þ At the end of this subsection, we define a real parameter 2E ϵ0 and a phase αϵ, ϵ0≡  Δm2 ee αϵ ≡ Arg ; ð ˆH1Þ23 2E Δm2 ee ð ˆH1Þ23  : ð25Þ Obviously, ϵ0 ∼ ϵ and ð ˆH1Þ23 ¼ eiαϵϵ0Δm2 ee=2E. It is not hard to see that in the Standard Model ϵ0 ¼ jϵ sinð˜θ13 − θ13Þs12c12j, which reconciles with the one defined in Ref. [5]. The two new defined parameters will frequently emerge in the following sections. 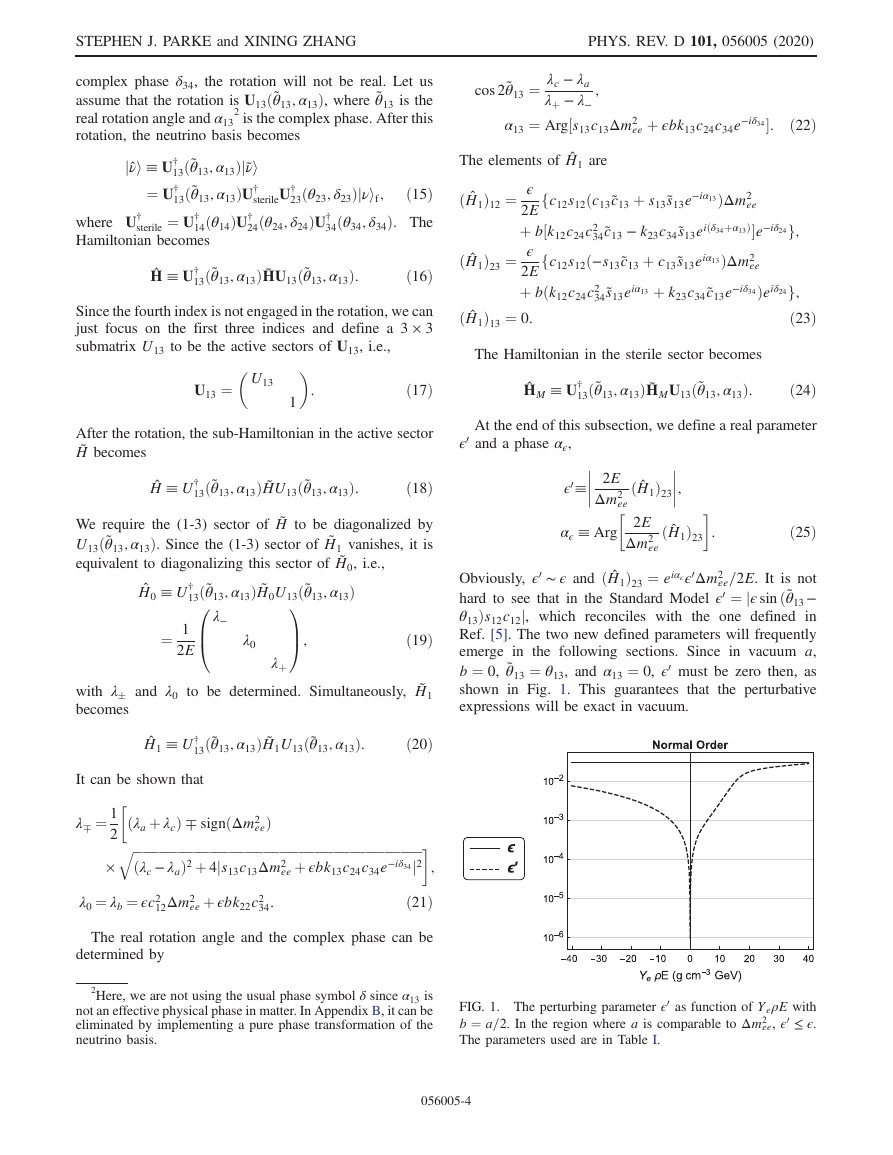Since in vacuum a, b ¼ 0, ˜θ13 ¼ θ13, and α13 ¼ 0, ϵ0 must be zero then, as shown in Fig. 1. This guarantees that the perturbative expressions will be exact in vacuum. 13ð˜θ13; α13Þj˜νi 13ð˜θ13; α13ÞU† 14ðθ14ÞU† jˆνi ≡ U† ¼ U† sterile ¼ U† where U† Hamiltonian becomes ˆH ≡ U† sterile 23ðθ23; δ23Þjνif; U† ð15Þ 34ðθ34; δ34Þ. The 24ðθ24; δ24ÞU† 13ð˜θ13; α13Þ ˜HU13ð˜θ13; α13Þ: ð16Þ Since the fourth index is not engaged in the rotation, we can just focus on the first three indices and define a 3 × 3 submatrix U13 to be the active sectors of U13, i.e.,  U13 U13 ¼  : 1 After the rotation, the sub-Hamiltonian in the active sector ˜H becomes ˆH ≡ U† 13ð˜θ13; α13Þ ˜HU13ð˜θ13; α13Þ: ð18Þ ˜H to be diagonalized by ˜H1 vanishes, it is ˜H0, i.e., We require the (1-3) sector of U13ð˜θ13; α13Þ. Since the (1-3) sector of equivalent to diagonalizing this sector of 1 CA; 0 13ð˜θ13; α13Þ ˜H0U13ð˜θ13; α13Þ B@ λ− ˆH0 ≡ U† λ0 ¼ 1 2E ð19Þ λþ with λ and λ0 to be determined. Simultaneously, becomes ˜H1 ˆH1 ≡ U† 13ð˜θ13; α13Þ ˜H1U13ð˜θ13; α13Þ: ð20Þ It can be shown that λ∓ ¼ 1 2 ×  ðλa þ λcÞ∓ signðΔm2 eeÞ q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ðλc − λaÞ2 þ 4js13c13Δm2 ee þ ϵbk13c24c34e−iδ34j2 ; ð21Þ ee þ ϵbk22c2 34: 12Δm2  λ0 ¼ λb ¼ ϵc2 The real rotation angle and the complex phase can be determined by 2Here, we are not using the usual phase symbol δ since α13 is not an effective physical phase in matter. In Appendix B, it can be eliminated by implementing a pure phase transformation of the neutrino basis. FIG. 1. The perturbing parameter ϵ0 as function of YeρE with b ¼ a=2. In the region where a is comparable to Δm2 ee, ϵ0 ≤ ϵ. The parameters used are in Table I. 056005-4
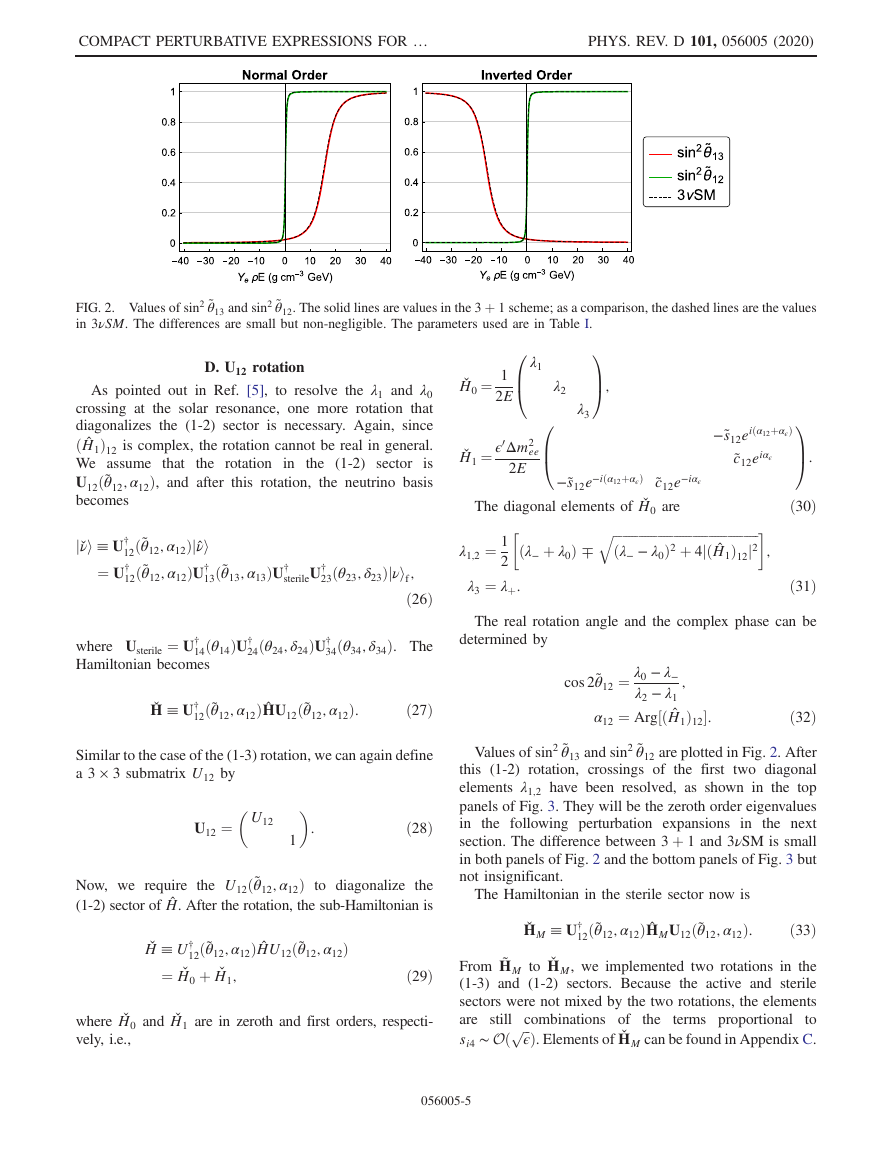
    COMPACT PERTURBATIVE EXPRESSIONS FOR … PHYS. REV. D 101, 056005 (2020) FIG. 2. Values of sin2 ˜θ13 and sin2 ˜θ12. The solid lines are values in the 3 þ 1 scheme; as a comparison, the dashed lines are the values in 3νSM. The differences are small but non-negligible. The parameters used are in Table I. 1 CA; λ2 λ3 0 B@ λ1 0 B@ ee ˇH0 ¼ 1 2E 2E ˇH1 ¼ ϵ0Δm2  λ1;2 ¼ 1 2 λ3 ¼ λþ: −˜s12e−iðα12þαϵÞ The diagonal elements of ˜c12e−iαϵ ˇH0 are q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ðλ− − λ0Þ2 þ 4jð ˆH1Þ12j2 ðλ− þ λ0Þ ∓ 1 CA: −˜s12eiðα12þαϵÞ ˜c12eiαϵ  ; ð30Þ ð31Þ D. U12 rotation As pointed out in Ref. [5], to resolve the λ1 and λ0 crossing at the solar resonance, one more rotation that diagonalizes the (1-2) sector is necessary. Again, since ð ˆH1Þ12 is complex, the rotation cannot be real in general. is We assume that U12ð˜θ12; α12Þ, and after this rotation, the neutrino basis becomes the rotation in the (1-2) sector jˇνi ≡ U† ¼ U† 12ð˜θ12; α12Þjˆνi 12ð˜θ12; α12ÞU† 13ð˜θ13; α13ÞU† sterile 23ðθ23; δ23Þjνif; U† ð26Þ where Usterile ¼ U† Hamiltonian becomes ˇH ≡ U† 14ðθ14ÞU† 24ðθ24; δ24ÞU† 34ðθ34; δ34Þ. The 12ð˜θ12; α12Þ ˆHU12ð˜θ12; α12Þ: ð27Þ Similar to the case of the (1-3) rotation, we can again define a 3 × 3 submatrix U12 by  U12 U12 ¼  : 1 ð28Þ Now, we require the U12ð˜θ12; α12Þ to diagonalize the (1-2) sector of ˆH. After the rotation, the sub-Hamiltonian is ˇH ≡ U† 12ð˜θ12; α12Þ ˆHU12ð˜θ12; α12Þ ¼ ˇH0 þ ˇH1; ð29Þ where ˇH0 and ˇH1 are in zeroth and first orders, respecti- vely, i.e., The real rotation angle and the complex phase can be determined by cos 2˜θ12 ¼ λ0 − λ− λ2 − λ1 ; α12 ¼ Arg½ð ˆH1Þ12Š: ð32Þ Values of sin2 ˜θ13 and sin2 ˜θ12 are plotted in Fig. 2. After two diagonal this (1-2) rotation, crossings of the first elements λ1;2 have been resolved, as shown in the top panels of Fig. 3. They will be the zeroth order eigenvalues in the following perturbation expansions in the next section. The difference between 3 þ 1 and 3νSM is small in both panels of Fig. 2 and the bottom panels of Fig. 3 but not insignificant. ˇHM ≡ U† The Hamiltonian in the sterile sector now is 12ð˜θ12; α12Þ ˆHMU12ð˜θ12; α12Þ: ð33Þ From ˜HM to ˇHM, we implemented two rotations in the (1-3) and (1-2) sectors. Because the active and sterile sectors were not mixed by the two rotations, the elements are still combinations of to si4 ∼ Oð ffiffiffi ϵp Þ. Elements of ˇHM can be found in Appendix C. the terms proportional 056005-5
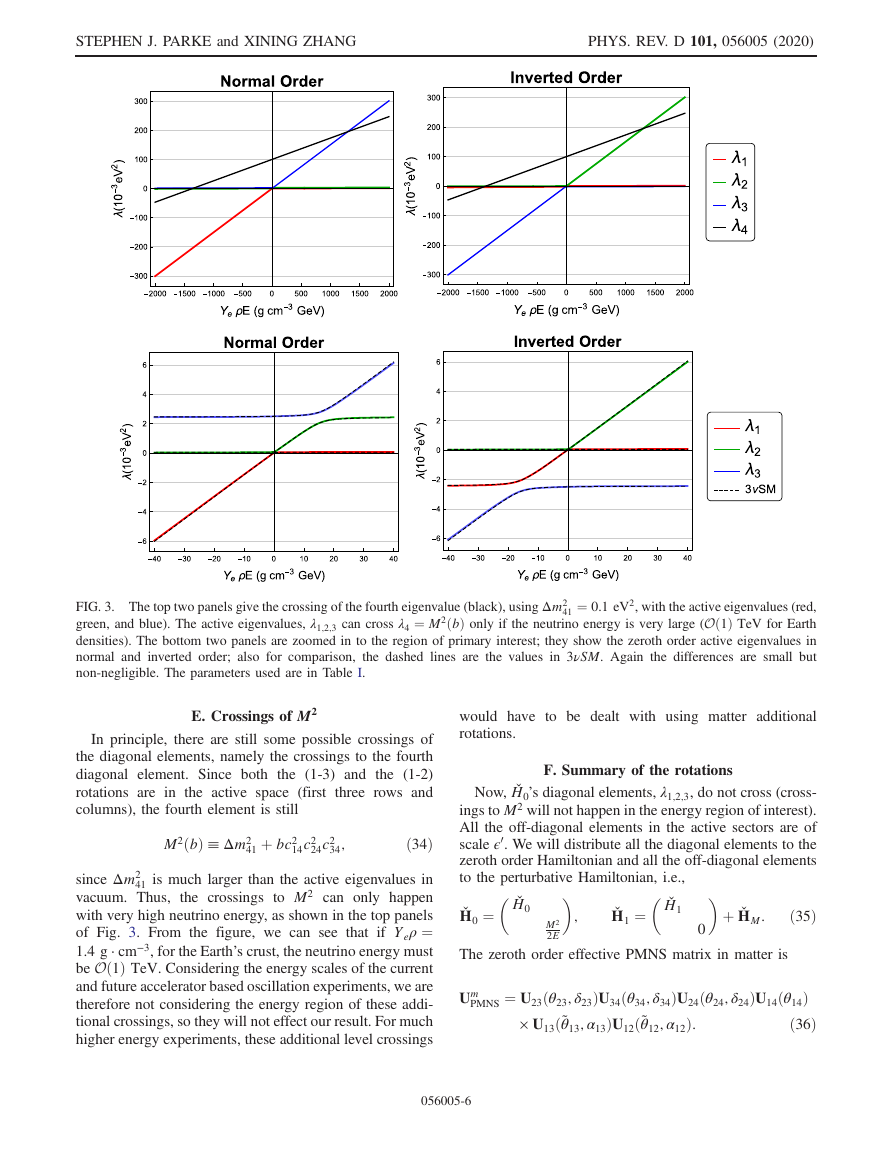
    STEPHEN J. PARKE and XINING ZHANG PHYS. REV. D 101, 056005 (2020) 41 ¼ 0.1 eV2, with the active eigenvalues (red, FIG. 3. The top two panels give the crossing of the fourth eigenvalue (black), using Δm2 green, and blue). The active eigenvalues, λ1;2;3 can cross λ4 ¼ M2ðbÞ only if the neutrino energy is very large (Oð1Þ TeV for Earth densities). The bottom two panels are zoomed in to the region of primary interest; they show the zeroth order active eigenvalues in normal and inverted order; also for comparison, the dashed lines are the values in 3νSM. Again the differences are small but non-negligible. The parameters used are in Table I. E. Crossings of M2 In principle, there are still some possible crossings of the diagonal elements, namely the crossings to the fourth diagonal element. Since both the (1-3) and the (1-2) rotations are in the active space (first three rows and columns), the fourth element is still 41 þ bc2 M2ðbÞ ≡ Δm2 24c2 34; ð34Þ 14c2 since Δm2 41 is much larger than the active eigenvalues in the crossings to M2 can only happen vacuum. Thus, with very high neutrino energy, as shown in the top panels of Fig. 3. From the figure, we can see that if Yeρ ¼ 1.4 g · cm−3, for the Earth’s crust, the neutrino energy must be Oð1Þ TeV. Considering the energy scales of the current and future accelerator based oscillation experiments, we are therefore not considering the energy region of these addi- tional crossings, so they will not effect our result. For much higher energy experiments, these additional level crossings would have to be dealt with using matter additional rotations. F. Summary of the rotations Now, ˇH0’s diagonal elements, λ1;2;3, do not cross (cross- ings to M2 will not happen in the energy region of interest). All the off-diagonal elements in the active sectors are of scale ϵ0. We will distribute all the diagonal elements to the zeroth order Hamiltonian and all the off-diagonal elements to the perturbative Hamiltonian, i.e., ˇH0 ¼  ˇH1  ˇH0 þ ˇHM: ˇH1 ¼  ;  0 ð35Þ M2 2E The zeroth order effective PMNS matrix in matter is PMNS ¼ U23ðθ23; δ23ÞU34ðθ34; δ34ÞU24ðθ24; δ24ÞU14ðθ14Þ Um ð36Þ × U13ð˜θ13; α13ÞU12ð˜θ12; α12Þ: 056005-6
    COMPACT PERTURBATIVE EXPRESSIONS FOR … PHYS. REV. D 101, 056005 (2020) TABLE I. Mixing parameters and vacuum eigenvalues used for the numerical calculations [20–23]. In different conventions to define the PMNS matrix [orders of U23 and Usterile, where Usterile ¼ U34U24U14, see Eq. (6)], some of the parameters are different; formulas to relate the parameters in both conventions are in Appendix A. In both conventions, the energy eigenvalues 31 ¼ 2.5 × 10−3 eV2, in vacuum are Δm2 41 ¼ 0.1 eV2. and Δm2 UPMNS≡ δ24=π s2 12 s2 s2 UsterileU23U13U12 0.3 0.02 0.44 −0.40 0.02 0.01 0.10 0.1 U23UsterileU13U12 21 ¼ 7.5 × 10−5 eV2, Δm2 0.02 0.50 0.09 0.08 0.49 −0.39 δ34=π s2 24 s2 23 δ23=π s2 14 0 13 34 First order corrections to the eigenstates are determined by Wi defined in Eq. (37), which are 8< : 0 − 2Eð ˇH1Þij λi−λj ðW1Þij ¼ i ¼ j i ≠ j : ð40Þ formulas of The detailed first and second order the perturbation expansions can be found in Appendix D. In general, with crossings of the zeroth order eigenvalues ruled out, perturbative expansions can go to arbitrary precision. However, numerical tests will suggest that it is sufficient to terminate the approach at second order. A. Numerical precision test We now test the accuracy of our perturbative expres- sions. We choose the νμ → νe channel and 1300 km baseline of DUNE to do the numerical test. The density of the Earth crust is chosen to be Yeρ ¼ 1.4 g · cm−3, b ¼ a=2, and all the mixing parameters are listed in Table I. The exact oscillation probabilities can be figured out by Ref. 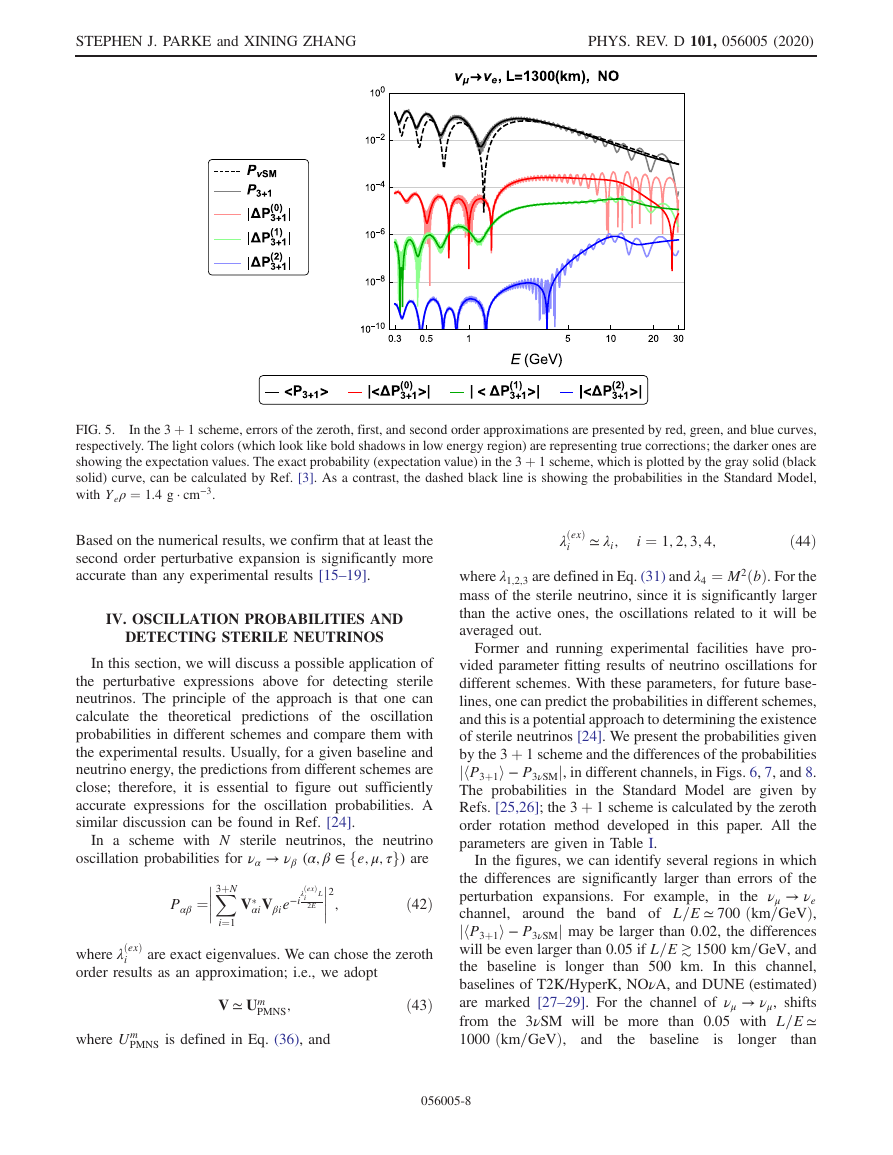[3] or given by a computer algebra system.3 The results are shown in Fig. 5. The error in the zeroth order expression is expected to be no more than ϵ ∼ 10−2, which is confirmed by the red curve in the plot. The green curve depicts the error of the first order perturbative expansion, which is under ϵ2 ∼ 10−4. To second order, the error further declines to ϵ3 ∼ 10−6, which also coincides with the prediction. In Fig. 5, the expectation values are obtained by averaging over the fast oscillation terms, i.e., the terms to ðλ4 − λiÞ. More with angular velocities proportional specifically,  ðλ4 − λiÞL 2E ¼ 0;   sin2 ðλ4 − λiÞL 4E  sin = cos ¼ 1 : 2 ð41Þ 3Only considering the 3 þ 1 scheme, an analytical solution is still possible since one just needs solve a quartic equation, but it is not the case for schemes with more sterile neutrinos. FIG. 4. Summary of the rotations and the following perturba- tive expansions. We first implemented vacuum rotations in the (2-3) and sterile sectors. The red circle with text sterile inside indicates the rotations in sterile rotations, the rotations represented by Usterile ¼ U34U24U14; see Eq. (6). Then, two matter rotations in the (1-3) and (1-2) sectors were performed. After the series of rotations, the zeroth order approximations of the eigenvalues and eigenvectors achieved OðϵÞ accuracy. Perturbative expansions will be used to further improve the precision. i.e., Since all possible degeneracies have been removed in the energy scale in which we are interested, we are free to implement a perturbation expansion to achieve even better accuracy. The process of reducing errors by performing rotations and perturbative expansions is summarized in Fig. 4. is more complicated, For the scenario with more than one sterile neutrino, although it the rotation method developed here is still applicable. In the convention of Eq. (5) Usterile will be changed if more sterile neutrinos are added. III. PERTURBATIVE EXPRESSIONS Since all the crossings of the zeroth order eigenvalues have been resolved (except for the crossings with M2, which are not in the energy region of interest) by the rotations and all the off-diagonal elements are small, we can now calculate the higher order corrections to the eigenval- ues and eigenvectors by perturbation methods. We define V to be the exact PMNS matrix in matter. It can be related to the zeroth order Um PMNS by PMNSð1 þ W1 þ W2 þ Þ; V ¼ Um ð37Þ where Wn is nth order correction. The exact eigenvalues are λðexÞ i ¼ λi þ λð1Þ i þ λð2Þ i þ  ; i ¼ 1; 2; 3; 4; ð38Þ where λ1;2;3 are defined in Eq. (31) and λ4 ¼ M2, λðnÞ nth order correction. i First order corrections to the eigenvalues are λð1Þ i ¼ 2Eð ˇH1Þii ¼ 0: is the ð39Þ 056005-7
    STEPHEN J. PARKE and XINING ZHANG PHYS. REV. D 101, 056005 (2020) In the 3 þ 1 scheme, errors of the zeroth, first, and second order approximations are presented by red, green, and blue curves, FIG. 5. respectively. The light colors (which look like bold shadows in low energy region) are representing true corrections; the darker ones are showing the expectation values. The exact probability (expectation value) in the 3 þ 1 scheme, which is plotted by the gray solid (black solid) curve, can be calculated by Ref. [3]. As a contrast, the dashed black line is showing the probabilities in the Standard Model, with Yeρ ¼ 1.4 g · cm−3. Based on the numerical results, we confirm that at least the second order perturbative expansion is significantly more accurate than any experimental results [15–19]. IV. OSCILLATION PROBABILITIES AND DETECTING STERILE NEUTRINOS In this section, we will discuss a possible application of the perturbative expressions above for detecting sterile neutrinos. The principle of the approach is that one can calculate the theoretical predictions of the oscillation probabilities in different schemes and compare them with the experimental results. Usually, for a given baseline and neutrino energy, the predictions from different schemes are close; therefore, it is essential to figure out sufficiently accurate expressions for the oscillation probabilities. A similar discussion can be found in Ref. [24]. In a scheme with N sterile neutrinos, the neutrino oscillation probabilities for να → νβ (α; β ∈ fe; μ; τg) are X3þN i¼1 Pαβ ¼ 2 V αiVβie−i λðexÞ i 2E L ; ð42Þ where λðexÞ order results as an approximation; i.e., we adopt are exact eigenvalues. We can chose the zeroth i V ≃ Um PMNS ; ð43Þ where Um PMNS is defined in Eq. (36), and λðexÞ i ≃ λi; i ¼ 1; 2; 3; 4; ð44Þ where λ1;2;3 are defined in Eq. (31) and λ4 ¼ M2ðbÞ. For the mass of the sterile neutrino, since it is significantly larger than the active ones, the oscillations related to it will be averaged out. Former and running experimental facilities have pro- vided parameter fitting results of neutrino oscillations for different schemes. With these parameters, for future base- lines, one can predict the probabilities in different schemes, and this is a potential approach to determining the existence of sterile neutrinos [24]. We present the probabilities given by the 3 þ 1 scheme and the differences of the probabilities jhP3þ1i − P3νSMj, in different channels, in Figs. 6, 7, and 8. The probabilities in the Standard Model are given by Refs. [25,26]; the 3 þ 1 scheme is calculated by the zeroth order rotation method developed in this paper. All the parameters are given in Table I. In the figures, we can identify several regions in which the differences are significantly larger than errors of the in the νμ → νe perturbation expansions. For example, channel, around the band of L=E ≃ 700 ðkm=GeVÞ, jhP3þ1i − P3νSMj may be larger than 0.02, the differences will be even larger than 0.05 if L=E ≳ 1500 km=GeV, and the baseline is longer than 500 km. In this channel, baselines of T2K/HyperK, NOνA, and DUNE (estimated) are marked [27–29]. For the channel of νμ → νμ, shifts from the 3νSM will be more than 0.05 with L=E ≃ 1000 ðkm=GeVÞ, than and the baseline longer is 056005-8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料