基于 ARMA 模型的中国钢铁价格预测研究 http://www.paper.edu.cn 1 辽宁工程技术大学工商管理学院，辽宁阜新（123000） 2 辽宁工程技术大学理学院，辽宁阜新（123000） 刘斌 1 ，盖如栋 2 E-mail：liubinreal@tom.com 摘 要：文中用 ARMA 模型，对 1995 年至 2005 年全国钢铁综合价格进行时间序列分析， 用 MATLAB 软件检验模型的可行性，并进行预测应用。结果表明，基于 ARMA 模型的中 国钢铁价格的模拟值和真实值较吻合。 关键词：ARMA 模型 钢铁综合价格 平稳时间序列 预测 1 前言 近年来，随着国家对基础产业的政策倾斜性扶持，国内钢铁需求量激增，国内钢铁价格 也随之攀升，特别是 2004 年以来，由于煤矿瓦斯爆炸等特大事故频频发生，国家强制性的 关闭中小煤矿，作为钢铁产业的原料的煤的价格也随之上涨，钢铁价格升起也是在所难免的。 国家出台了一系列的政策来压制钢铁价格的不合理上涨，从而能使钢铁价格在一个合理的和 市场可以接受的范围内进行波动，不至于让市场价格脱出国家的控制，造成市场的混乱。预 测研究一个现象的未来变化，是用该现象的过去行为来预测未来，即通过时间序列的历史数 据来揭示现象随时间变化的规律，将这种规律延伸到未来，从而对该现象的未来做出预测。 本文试图通过对 10 年中国每月历史数据的分析、拟合，并进行短期预测，从而为正确判断 未来价格趋势，制订相应对策来应对变化，对国家来说可以及时调整相关的钢铁政策，进一 步对价格进行宏观调控，对企业来说，及时调整对策来达到自己利益的最大化。 2 资料与方法 2.1 资料来源 自从 1985 年国家主持编制《中国钢铁工业年鉴》以来，年鉴的编制一直持续下来，未 曾中断。但是直到 1988 年，国家才对工业产品的价格进行市场化试点，经历两年之后国家 工业产品的价格才逐渐放开，并且逐步融入到市场中，1992 年工业产品价格的市场化才初 步步入正轨。本文的资料：1995 年至 2004 年的钢铁综合价格直接取自《中国钢铁工业年鉴》 的月综合价格 ]3[ ，2005 年及以后的价格根据国家编制综合价格的方法对原始数据计算得到 的，原始数据取自中国物资商情网 ]10[ 。对数据 5 由月价格加权平均成季价格 。 ]6[ 表 1 中国钢材的月综合价格 年 份 1 9 9 5 1 9 9 6 季 综合价格 1 2 3 4 1 2 3 4 3940.43 4141.43 4326.05 4397.81 4364.38 4368.81 4286.95 4195.29 年 份 1 9 9 8 1 9 9 9 季 综合价格 1 2 3 4 1 2 3 4 3671.09 3559.57 3446.24 3357.33 3306.91 3254.86 3218.86 3196.57 年 份 2 0 0 1 2 0 0 2 季 综合价格 1 2 3 4 1 2 3 4 3463.69 3451.3 3396.41 3293.41 3203.81 3306.52 3391.57 3494.95 年 份 2 0 0 4 2 0 0 5 季 综合价格 1 2 3 4 1 2 3 4 4524.27 4584.97 4702.07 4780.4 4991.1 5143.13 4728.53 4002.7 -1- 

http://www.paper.edu.cn 1 9 9 7 1 2 3 4 4045.66 3952.38 3812.67 3737.62 2 0 0 0 1 2 3 4 3206.63 3502.03 3474.41 3463.8 2 0 0 3 1 2 3 4 3833.67 3885.09 4065.29 4283 2 0 0 6 1 2 3 4 3840.43 2.2 ARMA 模型预测方法 ]4[ ]5[ ARMA 模型是一种比较成熟的模型，适于短期预测。模型建立，要求时间序列是随机 和平稳的，而且需要长期连续数据，编写程序进行模型的辨识。 2.2.1 AR 模型 AR 模型也称为自回归模型，它的预测方式是通过过去的观测值和现在的干扰值的线性 组合预测。自回归模型的数学公式为: x t p = ∑ x φ mtm 0 m − = + te , t ≥ p ]1[ 在 AR 模型中，序列 }{ tx 的当前值由序列 }{ te 的当前值和序列 }{ tx 的前一个长度为 p 的窗口内序列值决定。 2.2.2 MA 模型 MA 模型也称为滑动平均模型，它的预测方式是通过过去的干扰值和现在的干扰值的线 性组合预测 ]1[ 。 滑动平均模型的数学公式为: x t = −∑ b e εεε ntn t 1 e t + = 0 q n = 0 + ...... + e ε qtq − , t ≥ q 1 − 这个式子说明序列 } { tX 的当前值由序列 }{ te 从当前值前推长度为 q 的窗口内序列值决 定。 2.2.3 ARMA 模型 自回归模型和滑动平均模型的组合，便构成了用于描述平稳随机过程的自回归滑动平 均模型 ARMA. ARMA 由 AR 和 MA 两个部分组成，如下: x t = p ∑ x φ mtm 0 m − = + q ∑ e ε ntn − n = 0 , t ≥ p & t ≥ q ]2[ 在 ARMA 模型中，序列 }{ tx 的当前值由序列 }{ te 的当前值从当前值前推长度为 q 的窗 口内序列值以及序列 }{ tx 的前一个长度为 p 的窗口内序列值一起决定。 2.3 ARMA 模型的预测步骤 ]8[ (1)对时间序列进行差分，以得到一个平稳随机序列，然后 0-1 均值化序列。 (2)计算差分后序列的自相关系数和偏相关系数，以选择一个合适的 ARMA 模型。 (3)用最小二乘法对 ARMA 模型分析，计算模型参数值。 (4)对估计得到的模型，进行适应性检验，重新改进模型，直至得到最优模型为止。 (5)进行预测。 3 数据的拟合结果与讨论 -2- 

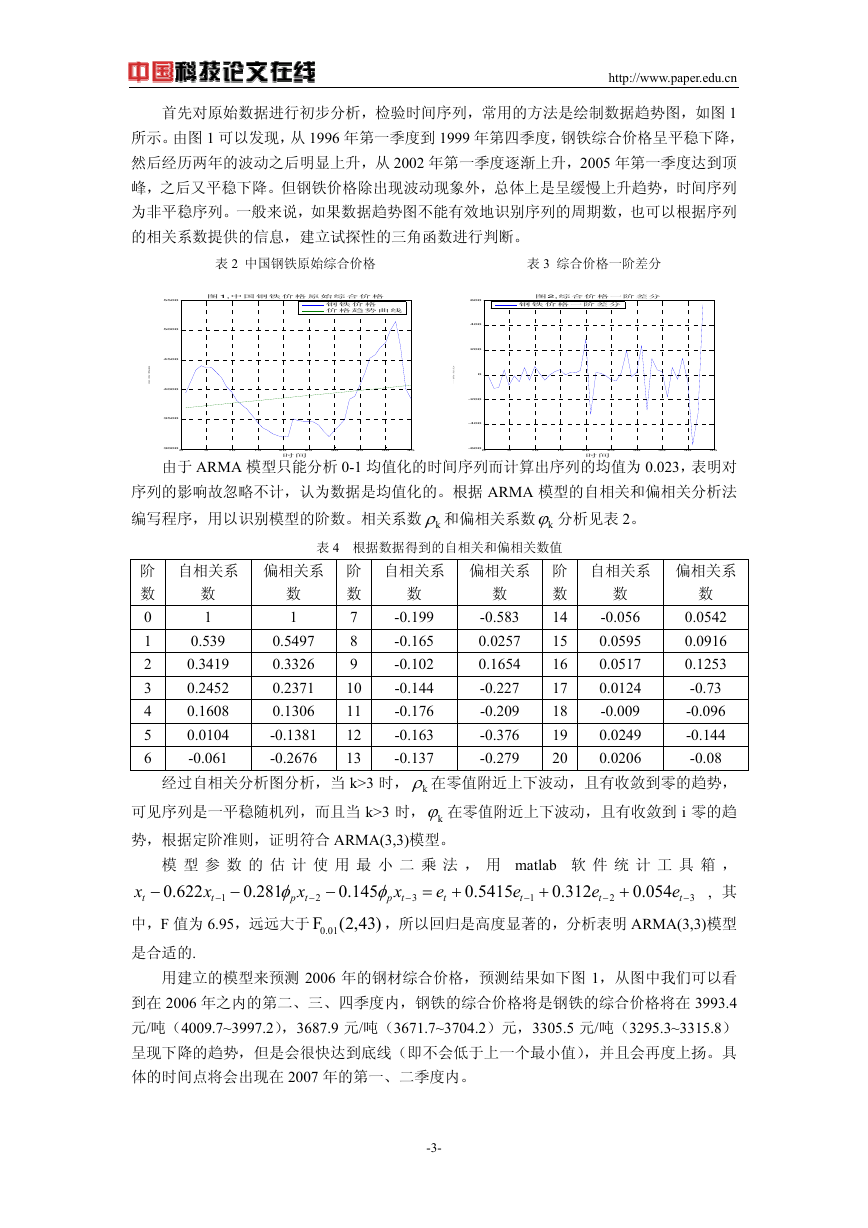
首先对原始数据进行初步分析，检验时间序列，常用的方法是绘制数据趋势图，如图 1 所示。由图 1 可以发现，从 1996 年第一季度到 1999 年第四季度，钢铁综合价格呈平稳下降， 然后经历两年的波动之后明显上升，从 2002 年第一季度逐渐上升，2005 年第一季度达到顶 峰，之后又平稳下降。但钢铁价格除出现波动现象外，总体上是呈缓慢上升趋势，时间序列 http://www.paper.edu.cn 5500 图 1,中国钢铁价格原始综合价格 为非平稳序列。一般来说，如果数据趋势图不能有效地识别序列的周期数，也可以根据序列 的相关系数提供的信息，建立试探性的三角函数进行判断。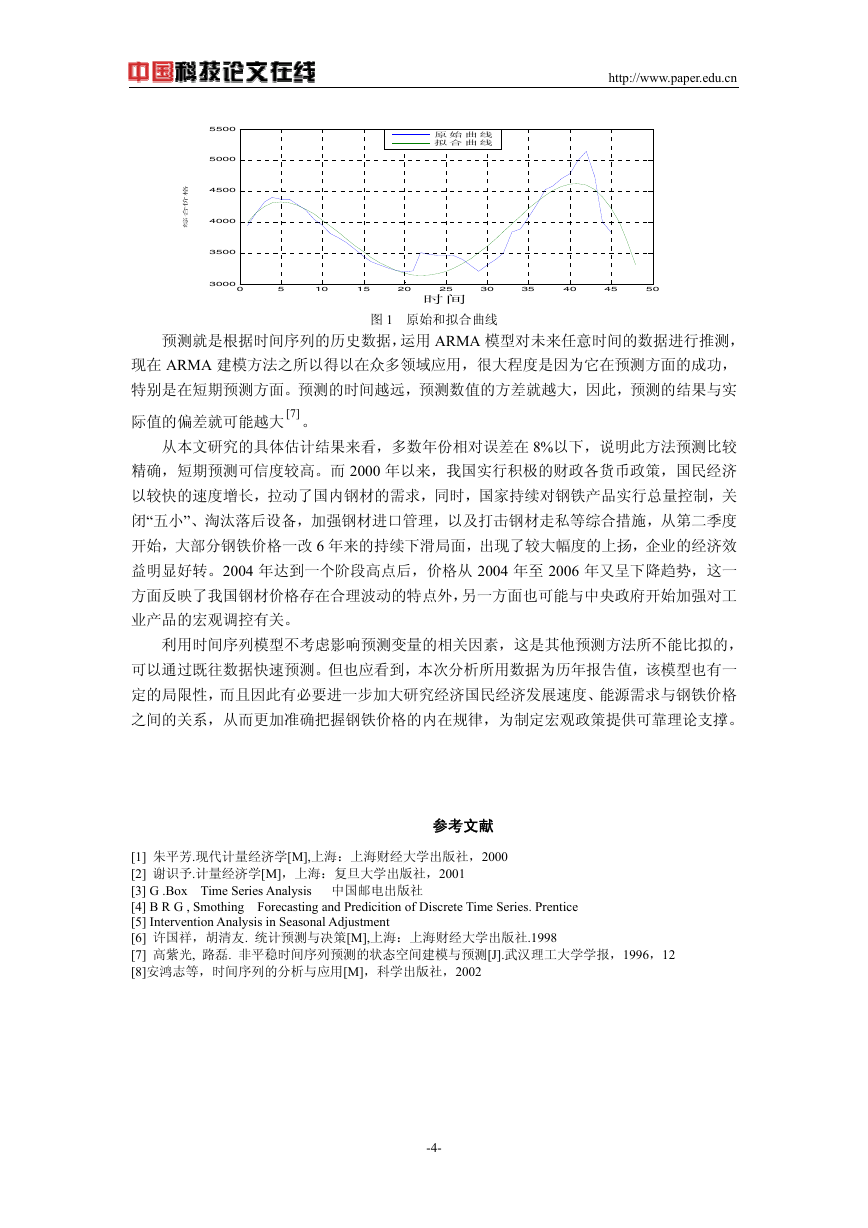 表 2 中国钢铁原始综合价格 表 3 综合价格一阶差分 钢铁价格 价格趋势曲线 图 2,综合价格一阶差分 钢铁价格一阶差分 3000 3500 4000 4500 5000 -600 -400 -200 据 数 始 原 15 20 30 35 20 25 30 35 10 15 40 45 40 45 5 10 0 5 分 差 阶 一 0 600 400 200 0 25 时间 由于 ARMA 模型只能分析 0-1 均值化的时间序列而计算出序列的均值为 0.023，表明对 序列的影响故忽略不计，认为数据是均值化的。根据 ARMA 模型的自相关和偏相关分析法 编写程序，用以识别模型的阶数。相关系数 kρ 和偏相关系数 kϕ 分析见表 2。 时间 数 数 数 1 数 1 偏相关系 自相关系 偏相关系 自相关系 阶 数 0 1 2 3 4 5 6 自相关系 偏相关系 数 数 表 4 根据数据得到的自相关和偏相关数值 阶 数 14 15 16 17 18 19 20 0.0542 0.0916 0.1253 -0.73 -0.096 -0.144 -0.08 经过自相关分析图分析，当 k>3 时， kρ 在零值附近上下波动，且有收敛到零的趋势， 可见序列是一平稳随机列，而且当 k>3 时， kϕ 在零值附近上下波动，且有收敛到 i 零的趋 势，根据定阶准则，证明符合 ARMA(3,3)模型。 -0.056 0.0595 0.0517 0.0124 -0.009 0.0249 0.0206 -0.583 0.0257 0.1654 -0.227 -0.209 -0.376 -0.279 0.5497 0.3326 0.2371 0.1306 -0.1381 -0.2676 -0.199 -0.165 -0.102 -0.144 -0.176 -0.163 -0.137 0.539 0.3419 0.2452 0.1608 0.0104 -0.061 阶 数 7 8 9 10 11 12 13 模 型 参 数 的 估 计 使 用 最 小 二 乘 法 ， 用 matlab 软 件 统 计 工 具 箱 ， 622.0 , 其 x tp ，所以回归是高度显著的，分析表明 ARMA(3,3)模型 e 054.0 t e 312.0 t e 5415 t 145.0 φ 2 )43,2(F 01.0 281.0 .0 x t e t + + + = − 1 − − − − 3 2 3 1 − − − x t φ x tp − 中，F 值为 6.95，远远大于 是合适的. 用建立的模型来预测 2006 年的钢材综合价格，预测结果如下图 1，从图中我们可以看 到在 2006 年之内的第二、三、四季度内，钢铁的综合价格将是钢铁的综合价格将在 3993.4 元/吨（4009.7~3997.2），3687.9 元/吨（3671.7~3704.2）元，3305.5 元/吨（3295.3~3315.8） 呈现下降的趋势，但是会很快达到底线（即不会低于上一个最小值），并且会再度上扬。具 体的时间点将会出现在 2007 年的第一、二季度内。 -3- 

格 价 合 综 5500 5000 4500 4000 3500 3000 0 http://www.paper.edu.cn 原 始 曲 线 拟 合 曲 线 5 10 15 20 25 30 35 40 45 50 时间 图 1 原始和拟合曲线 预测就是根据时间序列的历史数据，运用 ARMA 模型对未来任意时间的数据进行推测， 现在 ARMA 建模方法之所以得以在众多领域应用，很大程度是因为它在预测方面的成功， 特别是在短期预测方面。预测的时间越远，预测数值的方差就越大，因此，预测的结果与实 际值的偏差就可能越大 ]7[ 。 从本文研究的具体估计结果来看，多数年份相对误差在 8%以下，说明此方法预测比较 精确，短期预测可信度较高。而 2000 年以来，我国实行积极的财政各货币政策，国民经济 以较快的速度增长，拉动了国内钢材的需求，同时，国家持续对钢铁产品实行总量控制，关 闭“五小”、淘汰落后设备，加强钢材进口管理，以及打击钢材走私等综合措施，从第二季度 开始，大部分钢铁价格一改 6 年来的持续下滑局面，出现了较大幅度的上扬，企业的经济效 益明显好转。2004 年达到一个阶段高点后，价格从 2004 年至 2006 年又呈下降趋势，这一 方面反映了我国钢材价格存在合理波动的特点外，另一方面也可能与中央政府开始加强对工 业产品的宏观调控有关。 利用时间序列模型不考虑影响预测变量的相关因素，这是其他预测方法所不能比拟的， 可以通过既往数据快速预测。但也应看到，本次分析所用数据为历年报告值，该模型也有一 定的局限性，而且因此有必要进一步加大研究经济国民经济发展速度、能源需求与钢铁价格 之间的关系，从而更加准确把握钢铁价格的内在规律，为制定宏观政策提供可靠理论支撑。 参考文献 [1] 朱平芳.现代计量经济学[M],上海：上海财经大学出版社，2000 [2] 谢识予.计量经济学[M]，上海：复旦大学出版社，2001 [3] G .Box Time Series Analysis 中国邮电出版社 [4] B R G , Smothing Forecasting and Predicition of Discrete Time Series. Prentice [5] Intervention Analysis in Seasonal Adjustment [6] 许国祥，胡清友. 统计预测与决策[M],上海：上海财经大学出版社.1998 [7] 高紫光, 路磊. 非平稳时间序列预测的状态空间建模与预测[J].武汉理工大学学报，1996，12 [8]安鸿志等，时间序列的分析与应用[M]，科学出版社，2002 -4- 

http://www.paper.edu.cn Analysis of Time-series Forecast for Blend Price of Steel Based on ARMA Model Liu Bin，Gai Rudong Liaoning Technical University （123000） Abstract Using ARMA model, this paper analyzed the blend price of steel from 1995 to 2005 in China and verified the model by MATLAB. The results show that the related data forecast of blend price of steel in China is close to factual value. In application，ARMA model has an important role in decision- making for merchants. Keywords：ARMA model，blend price of steel， steady time-series， forecast -5-