Direct Simulation of Monte Carlo of Hypersonic Shock Interaction.pdf-资料库

weixin_38716460-12127965-4744300845396724330.pdf-第1页.png

第1页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第2页.png

第2页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第3页.png

第3页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第4页.png

第4页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第5页.png

第5页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第6页.png

第6页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第7页.png

第7页 / 共15页

weixin_38716460-12127965-4744300845396724330.pdf-第8页.png

第8页 / 共15页

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn Direct Simulation of Monte Carlo of Hypersonic Shock Interaction# XIAO Hong, WU Di* (School of Power and Energy, Northwestern Polytechnical University, Xi’an710072) Abstract: Direct Simulation of Monte Carlo (DSMC) of hypersonic shock interaction was present. Molecule models in DSMC included hard sphere, variable hard sphere and variable soft sphere. Double-cone and Edney’s type IV shock interaction was selected in DSMC research. Comparisons between DSMC and experiment were also conducted. Investigation of double-cone hypersonic flow shows that three collisions models can predict the trend of pressure coefficient and standun number. The agreement between DSMC simulation and experiment is best by hard sphere collisions model. Investigation of type IV shock interaction shows that the agreement between DSMC simulation and experiment is generally good in hard sphere and variable hard sphere collisions model. But it is unsuccessfully in variable soft sphere. Both double-cone flow and type IV shock interaction simulation shows that DSMC error depend on Kn Number and models employed for intermolecular interaction. With the Kn number increasing, DSMC error is decreasing. The error are the smallest for hard sphere model in comprised with variable hard sphere model and variable soft sphere model. When Kn number exceeds8.0 ×〖10〗^(-5), DSMC error for pressure coefficient ,stanton number and scale of interaction region is controlled within 10%.(10 Points, Times New Roman) Key words: Mechanics; DSMC; Shock interaction; Double-cone flow; type IV shock interaction; Experimental validation 0 Introduction Shock interactions play an important role in hypersonic flows. In the past decade, there have been signification efforts in computational fluid dynamics to develop prediction techniques for simulating these complex flow structures [1][2][3]. Most these works were simulated using the continuum transport equations (Navier-Stokes), which describe the transport of mass, momentum and energy. These equations are based on the hypothesis that the mean free path length of the gas molecules is very small in comparison to a characteristic dimension L of the flow. This dimension can be the gradient length scale as flowing. φ ∂⎛ ⎞ ⎜ ⎟∂⎝ x ⎠ L= / φ On which some flow property φ changes significantly. The dimensionless Knudsen number Kn can be used to describe this situation: λKn= L Flows with Kn > 10 are called “free molecular flows”. In this regime, inter-molecular collisions rarely occur and the flow is completely dominated by the inter-action between the gas and the walls. Flows in the free molecular regime can be simulated using Molecular Dynamics(MD) or ballistic models. In the intermediate ( 0.01 < Kn < 10 ) or rarefied regime, both collisions with solid surfaces and with other gas molecules are important, and therefore have to be included in the simulation to Foundations: Specialized Research Fund for the Doctoral Program of Higher Education(No.200806990021) Brief author introduction:XIAO Hong(1978-),Male,Associate Professor,Research Field:DSMC,LBM,Hypersonic CFD Simulation. E-mail: xhong@nwpu.edu.cn - 1 -

http://www.paper.edu.cn 中国科技论文在线 obtain an accurate result. The Direct Simulation Monte Carlo(DSMC) method as developed by Bird[6] is the only practical engineering method that can be used in the rarefied regime. The DSMC method is also valid in free molecular and continuum regimes, although the computational expenses become very large in the latter case. Its computational epenses, infact, scale with Kn-4and become prohibitively large when Kn becomes lower than0.05. In summary, one can simulate flows with Kn<0.01 using continuum based CFD models, and flows with Kn>0.05 with particle based DSMC methods, and with 0.05

中国科技论文在线 1.1 Particles Moving http://www.paper.edu.cn 85 In the first process, all the simulated molecules are moved through distances appropriate to their velocity components and the discrete time-step. Appropriate action is taken if the molecule crosses boundaries representing solid surfaces, or s symmetry boundary, or the outer boundary of the flow. Collisions with surfaces can be treated as being either fully specula, fully diffuse, or some combinations of the two. Secular collisions involve a simple reversal of the molecular velocity component normal to the incident surface. Diffuse collisions cause a random reorientation of the reflected molecule, where the post-collision velocity is based on the temperature of the surface. 90 95 100 Fig.1 Flowchart of DSMC 1.2 Indexing and Tracking the Particles The second DSMC process involves indexing and tracking the particles. A scheme for molecular referencing is the prerequisite for the next two steps: modeling the collisions and sampling the flow field. 1.3 Simulation of the Collisions The third step, simulating the collisions, is an important process that sets DSMC apart from molecular dynamics simulation methods. In the DSMC simulation, elastic collision model was used In which there is no interchange of translational and internal energy. Linear momentum and energy was conserved in the collision. - 3 -

中国科技论文在线 1.3.1 Impact Parameters and Collision Cross-section http://www.paper.edu.cn The probability of a collision between two molecules in a homogenous gas is proportional to the product of their relative speed and total collision cross-section. In DSMC, the cross-section is specified as[9], 105 σ= b db dχ χ sin (1) Where, b is the distance of closest approach of undisturbed trajectories. χ is angle of deflection which showed in Fig.2. So that, the total collision cross-section is defined as, ∫ σ =2π σsinχdχ=2π bdb T ∫ π 0 (2) 110 In above formula, the distance of closest approach of undisturbed trajectories b is given by different models of molecules and inter-molecular forces. In this paper, three molecular models are used in the simulation. 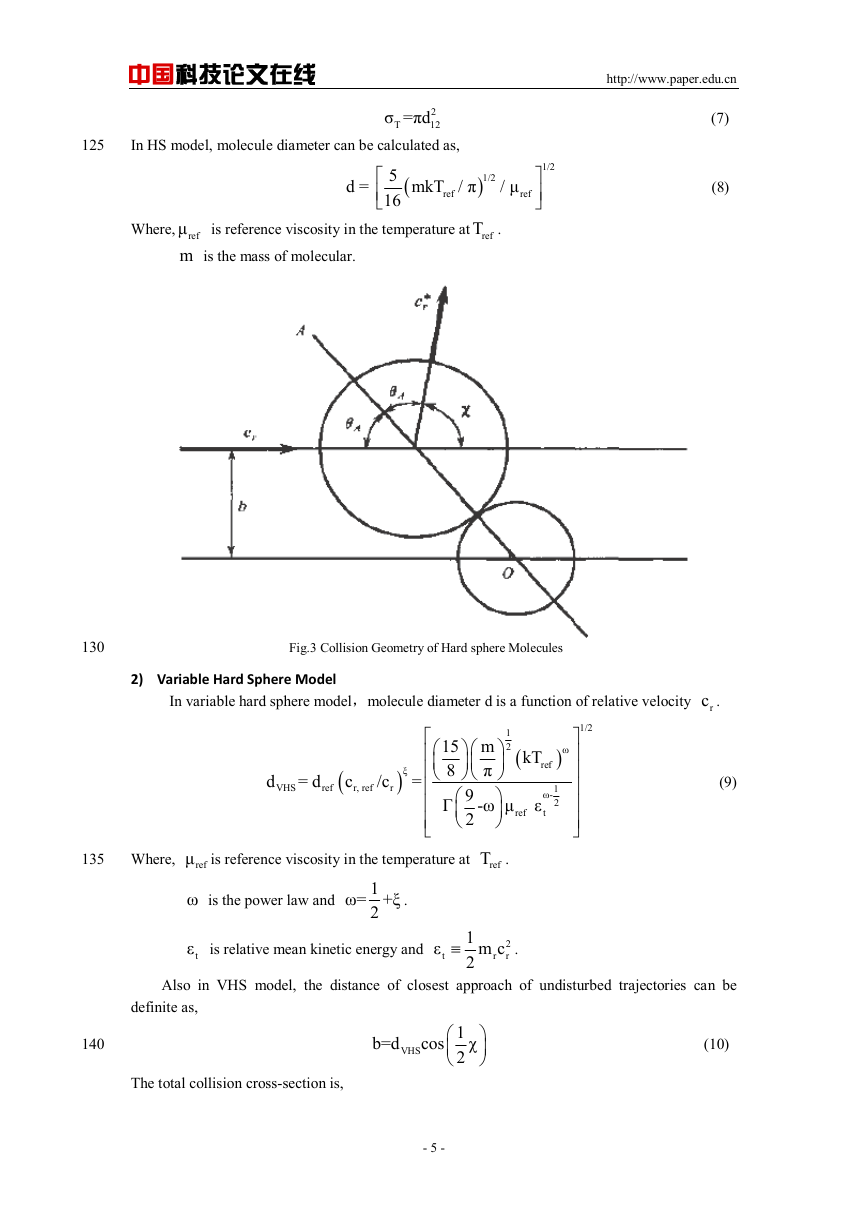115 1) Hard Sphere Model In hard sphere model, inter-molecular force is effective at Fig.2 Illustration of the impact parameters 1r= 2 ( d +d =d 1 12 2 ) (3) Therefore, 120 and b=d cos 12 1 2 ⎛ ⎜ ⎝ χ ⎞ ⎟ ⎠ (4) db/dχ = d sin 12 1 2 1 2 ⎛ ⎜ ⎝ χ ⎞ ⎟ ⎠ (5) σ=d /4 (6) 2 12 The total collision cross-section is, - 4 -

中国科技论文在线 http://www.paper.edu.cn 125 In HS model, molecule diameter can be calculated as, σ =πd (7) T 2 12 d = 5 16 ⎡ ⎢ ⎣ ( mkT / π ref 1/2 ) / µ ref 1/2 ⎤ ⎥ ⎦ (8) refµ is reference viscosity in the temperature at Where, m is the mass of molecular. refT . 130 Fig.3 Collision Geometry of Hard sphere Molecules rc . 2) Variable Hard Sphere Model In variable hard sphere model，molecule diameter d is a function of relative velocity d VHS = d ref ( c r, ref /c r ξ ) = ⎛ ⎜ ⎝ ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 15 m ⎞⎛ ⎟⎜ 8 π ⎠⎝ 9Γ ⎛ ⎜ 2 ⎝ ⎞ ⎟ ⎠ ⎞ ⎟ ⎠ -ω µ ε ref 1 2 ( kT ref ) 1ω- 2 t ω 1/2 ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (9) 135 Where, refµ is reference viscosity in the temperature at refT . ω is the power law and 1ω= +ξ 2 . tε is relative mean kinetic energy and ε t ≡ 1 2 m c r 2 r . Also in VHS model, the distance of closest approach of undisturbed trajectories can be definite as, 140 The total collision cross-section is, b=d cos VHS 1 2 ⎛ ⎜ ⎝ χ ⎞ ⎟ ⎠ (10) - 5 -

中国科技论文在线 http://www.paper.edu.cn σ =σ T T, ref ( d VHS /d ref )2 (11) σ T, ref is reference collision cross-section at reference molecule diameter refd . Where, 3) 145 Variable Soft Sphere Model In variable soft sphere model，molecule diameter d is defined as , 1/2 d VVS = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ( 5 α+1 α+2 )( kT ref ω ) 1 2 ( ) ⎞ ⎟ ⎠ ⎛ ⎜ ⎝ -ω µ ε m π ⎞ ⎟ ⎠ ref 1ω- 2 t 16αΓ 9 2 ⎛ ⎜ ⎝ ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (12) Where, α is scattering coefficient.(In case ofα=1, VSS model is same to VHS model.) In VSS model, the distance of closest approach of undisturbed trajectories can be definite as, b=d α cos VSS 1 2 ⎛ ⎜ ⎝ χ ⎞ ⎟ ⎠ (13) 150 The total collision cross-section is, σ =πd T 2 VSS (14) 1.3.2 Gas-Surface Interaction Diffuse reflection with full accommodation to the surface temperature is used in the 155 160 165 simulation. On the other hand, molecules were diffused in the condition of Maxwell distribution at T = T in the simulation. W 1.4 Sampling The final process is sampling the macroscopic flow properties. The spatial coordinates and velocity components of molecules in a particular cell are used to calculate macroscopic quantities at the geometric centre of the cell. ρ = nm (14) P = ρ c-c ( )2 (15) is number density of molecules. Where, c is velocity of molecule. c is average velocity of molecule. 1.5 Parameters Parameters selected in this paper are pressure coefficient and standun number. P 2 ∞ P - P C = 1 ρV ∞ 2 q S = 1 ρV t 3 ∞ 2 (16) (17) Where, P is the pressure of flow field. 170 P∞ is the far-field pressure of flow field. - 6 -

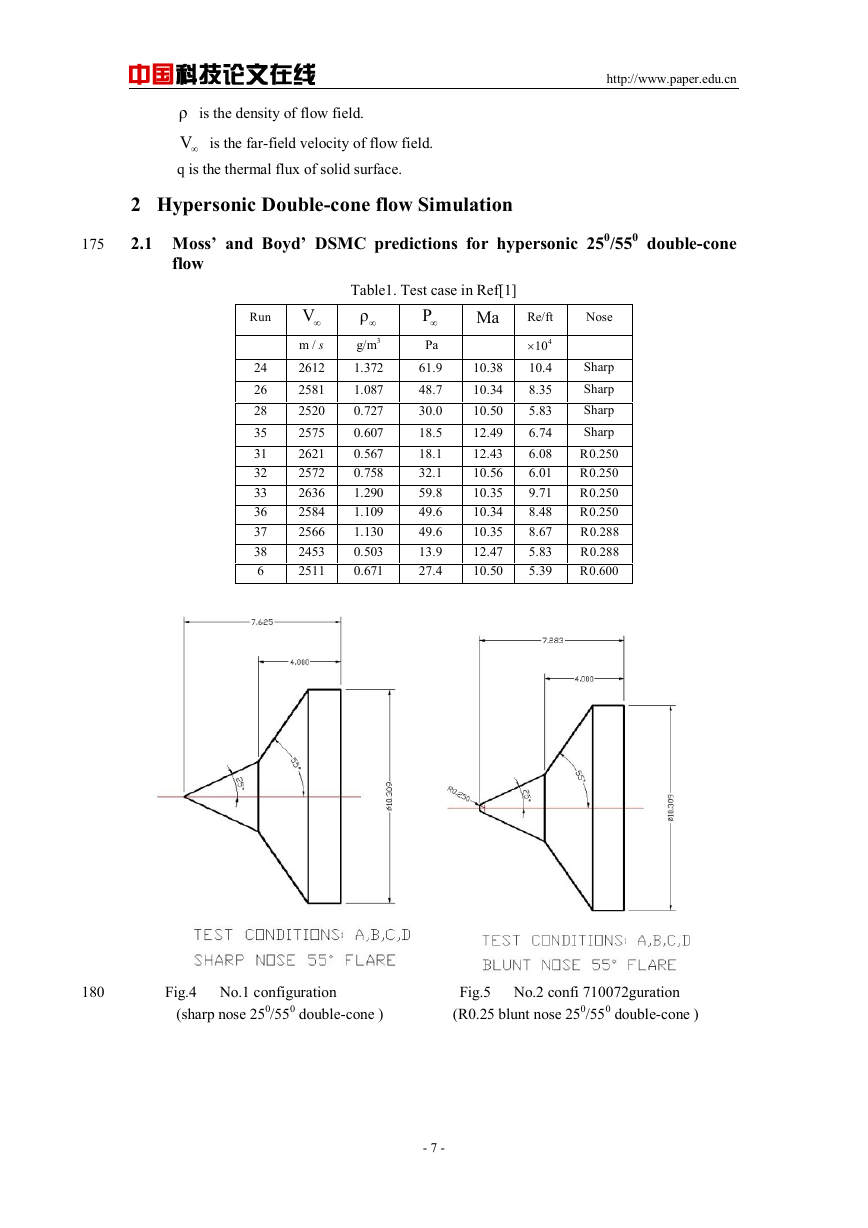
中国科技论文在线 ρ is the density of flow field. V∞ is the far-field velocity of flow field. q is the thermal flux of solid surface. http://www.paper.edu.cn 2 Hypersonic Double-cone flow Simulation 2.1 Moss’ and Boyd’ DSMC predictions for hypersonic 250/550 double-cone flow 175 Run V∞ m / s 2612 24 2581 26 28 2520 2575 35 2621 31 32 2572 2636 33 2584 36 2566 37 38 2453 2511 6 Table1. Test case in Ref[1] ρ∞ g/m 3 1.372 1.087 0.727 0.607 0.567 0.758 1.290 1.109 1.130 0.503 0.671 P∞ Pa 61.9 48.7 30.0 18.5 18.1 32.1 59.8 49.6 49.6 13.9 27.4 Ma 10.38 10.34 10.50 12.49 12.43 10.56 10.35 10.34 10.35 12.47 10.50 Re/ft 410× 10.4 8.35 5.83 6.74 6.08 6.01 9.71 8.48 8.67 5.83 5.39 Nose Sharp Sharp Sharp Sharp R0.250 R0.250 R0.250 R0.250 R0.288 R0.288 R0.600 180 Fig.4 No.1 configuration Fig.5 No.2 confi 710072guration (sharp nose 250/550 double-cone ) (R0.25 blunt nose 250/550 double-cone ) - 7 -

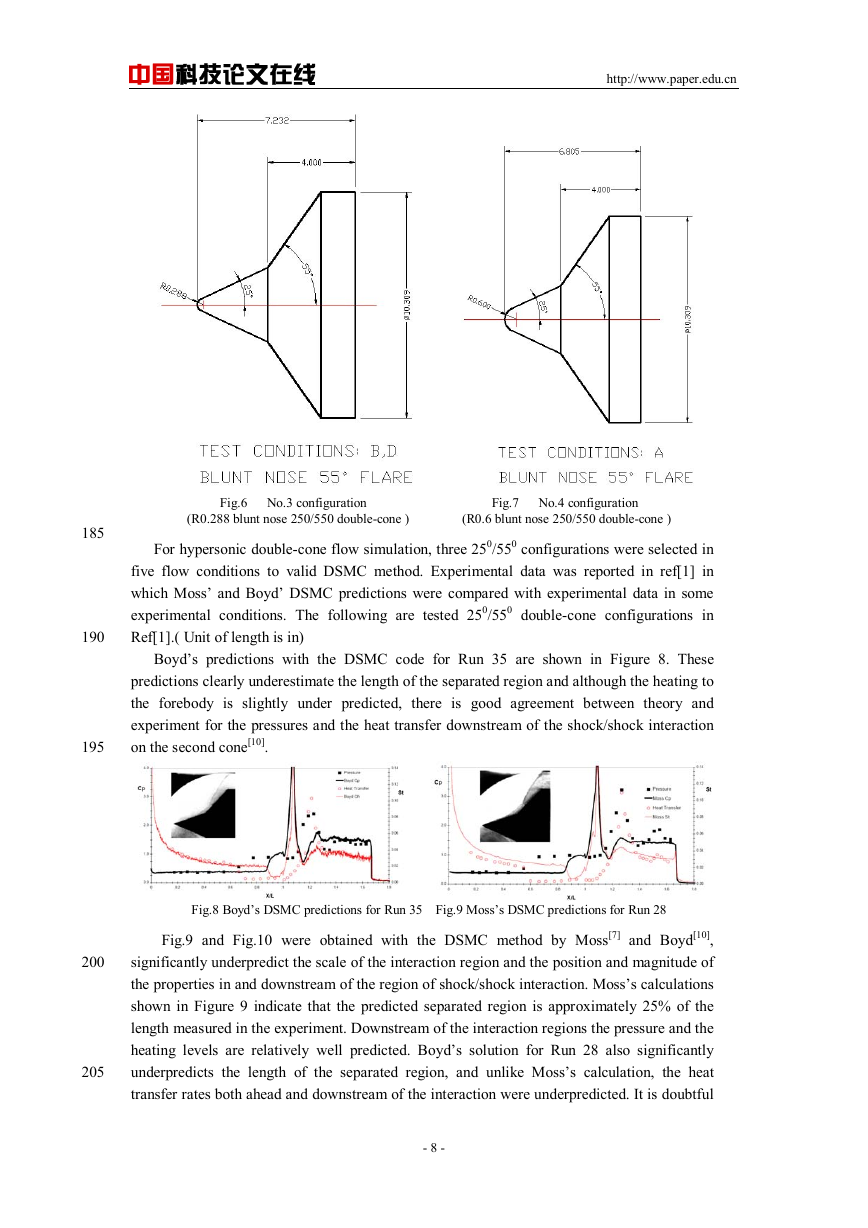
中国科技论文在线 http://www.paper.edu.cn 185 190 195 200 205 Fig.6 No.3 configuration Fig.7 No.4 configuration (R0.288 blunt nose 250/550 double-cone ) (R0.6 blunt nose 250/550 double-cone ) For hypersonic double-cone flow simulation, three 250/550 configurations were selected in five flow conditions to valid DSMC method. Experimental data was reported in ref[1] in which Moss’ and Boyd’ DSMC predictions were compared with experimental data in some experimental conditions. The following are tested 250/550 double-cone configurations in Ref[1].( Unit of length is in) Boyd’s predictions with the DSMC code for Run 35 are shown in Figure 8. These predictions clearly underestimate the length of the separated region and although the heating to the forebody is slightly under predicted, there is good agreement between theory and experiment for the pressures and the heat transfer downstream of the shock/shock interaction on the second cone[10]. Fig.8 Boyd’s DSMC predictions for Run 35 Fig.9 Moss’s DSMC predictions for Run 28 Fig.9 and Fig.10 were obtained with the DSMC method by Moss[7] and Boyd[10], significantly underpredict the scale of the interaction region and the position and magnitude of the properties in and downstream of the region of shock/shock interaction. Moss’s calculations shown in Figure 9 indicate that the predicted separated region is approximately 25% of the length measured in the experiment. Downstream of the interaction regions the pressure and the heating levels are relatively well predicted. Boyd’s solution for Run 28 also significantly underpredicts the length of the separated region, and unlike Moss’s calculation, the heat transfer rates both ahead and downstream of the interaction were underpredicted. It is doubtful - 8 -

资料库

Direct Simulation of Monte Carlo of Hypersonic Shock Interaction.pdf

相关推荐

开发技术

热门标签

最新资料