第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
《动手学——批量归一化和残差网络》笔记.pdf
《动手学——批量归一化和残差网络》笔记
《动手学
批量归一化和残差网络》笔记
批量归一化（BatchNormalization））
批量归一化（
ps 批量归一化本质上是对数据的标准化处理，输入标准化一般用于浅层模型，但是对于深层网络，输入的标准化不够，因为随着模型的迭代更新，依
然容易造成靠近输出层，它的数据是剧烈变化的。所以批量归一化的出现是应对深度模型的。
对输入的标准化（浅层模型）
对输入的标准化（浅层模型）
处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。
标准化处理输入数据使各个特征的分布相近
批量归一化（深度模型）
批量归一化（深度模型）
利用小批量上的均值和标准差，不断调整神经网络中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。
1.对全连接层做批量归一化
对全连接层做批量归一化
（形状 m×d，对m个元素做批量归一化）
位置：全连接层中的仿射变换和激活函数之间。
全连接：
全连接：
x=Wu+boutput=ϕ(x)
\boldsymbol{x} = \boldsymbol{W\boldsymbol{u} + \boldsymbol{b}} \\
output =\phi(\boldsymbol{x})
x=Wu+boutput=ϕ(x)
输入是u，大小为batchsize * 输入神经元个数。经过仿射变换后得到X，X大小为batchsize * 输出神经元个数，经过激活函数得到的output形状一样。
将批量归一化放在仿射变换之后，激活函数之前。
批量归一化：
批量归一化：
output=ϕ(BN(x))
output=\phi(\text{BN}(\boldsymbol{x}))output=ϕ(BN(x))
y(i)=BN(x(i))
\boldsymbol{y}^{(i)} = \text{BN}(\boldsymbol{x}^{(i)})
y(i)=BN(x(i))
μB←1m∑i=1mx(i),
\boldsymbol{\mu}_\mathcal{B} \leftarrow \frac{1}{m}\sum_{i = 1}^{m} \boldsymbol{x}^{(i)},
μB←m1i=1∑mx(i),
σB2←1m∑i=1m(x(i)−μB)2,
\boldsymbol{\sigma}_\mathcal{B}^2 \leftarrow \frac{1}{m} \sum_{i=1}^{m}(\boldsymbol{x}^{(i)} – \boldsymbol{\mu}_\mathcal{B})^2,
σB2←m1i=1∑m(x(i)−μB)2,
x^(i)←x(i)−μBσB2+ϵ,
\hat{\boldsymbol{x}}^{(i)} \leftarrow \frac{\boldsymbol{x}^{(i)} – \boldsymbol{\mu}_\mathcal{B}}{\sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}},
x^(i)←σB2+ϵx(i)−μB
,
这 ϵ > 0是个很小的常数，保证分母大于0
y(i)←γ⊙x^(i)+β.
{\boldsymbol{y}}^{(i)} \leftarrow \boldsymbol{\gamma} \odot
\hat{\boldsymbol{x}}^{(i)} + \boldsymbol{\beta}.
y(i)←γ⊙x^(i)+β.
引入可学习参数：拉伸参数γ和偏移参数β。若γ=σB2+ϵ\boldsymbol{\gamma} = \sqrt{\boldsymbol{\sigma}_\mathcal{B}^2 + \epsilon}γ=σB2+ϵ和
β=μB\boldsymbol{\beta} = \boldsymbol{\mu}_\mathcal{B}β=μB，批量归一化无效。
2.对卷积层做批量归
对卷积层做批量归 化化
位置：卷积计算之后、应 激活函数之前。
（形状 m×cxp×q，对每个通道的m×p×q个元素做批量归一化）
如果卷积计算输出多个通道，我们需要对这些通道的输出分别做批量归一化，且每个通道都拥有独立的拉伸和偏移参数。
计算：对单通道，batchsize=m,卷积计算输出=pxq
对该通道中m×p×q个元素同时做批量归一化,使用相同的均值和方差。
3.预测时的批量归
预测时的批量归 化化
训练：以batch为单位,对每个batch计算均值和方差。
预测：用移动平均估算整个训练数据集的样本均值和方差。
从零实现
从零实现
import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import torchvision
import sys
sys.path.append("/home/kesci/input/")
import d2lzh1981 as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#需要把X标准化为期望是0，方差是1的X_hat
def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 判断当前模式是训练模式还是预测模式
if not is_training: # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else: #如果是在训练模式下,以batch为单位,对每个batch计算均值和方差。然后对每个batch的X做标准化
assert len(X.shape) in (2, 4)
if len(X.shape) == 2: # 使用全连接层的情况，X是全连接层仿射变换的输出，计算特征维上的均值和方差
mean = X.mean(dim=0) # X=m*d，m就是batchsize，即在m上求均值和方差
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况，X=m*c*h*w，计算通道维上（axis=1）的均值和方差。对m*h*w个元素做均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
#通道有几个，mean有几维
var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
# 训练模式下用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差（移动平均：计算到每个batch时，通过更新的方法来使移动平均更接近整体的期望和方差）
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean #momentum是自己规定的动量，是超参数
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 拉伸和偏移
return Y, moving_mean, moving_var
#该类作用：维护学习参数和超参数
class BatchNorm(nn.Module):
def __init__(self, num_features, num_dims):
#输入 num_features：2全连接层（代表输出神经元个数）；4卷积层（代表通道数）
super(BatchNorm, self).__init__()
if num_dims == 2:
shape = (1, num_features) #全连接层输出神经元
else:
shape = (1, num_features, 1, 1) #通道数
# 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 不参与求梯度和迭代的变量，全在内存上初始化成0
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.zeros(shape)
def forward(self, X):
# 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
Y, self.moving_mean, self.moving_var = batch_norm(self.training,
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
基于基于LeNet的应用的应用
net = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
BatchNorm(6, num_dims=4), #通道数为6；4表示为卷积层后面的batch norm
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
BatchNorm(16, num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2, 2),
d2l.FlattenLayer(),
nn.Linear(16*4*4, 120),
BatchNorm(120, num_dims=2), #2表示为全连接层后面的batch norm
nn.Sigmoid(),
nn.Linear(120, 84),
BatchNorm(84, num_dims=2),
nn.Sigmoid(),
nn.Linear(84, 10)
)
print(net)
Sequential(
(0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(1): BatchNorm()
(2): Sigmoid()
(3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(5): BatchNorm()
(6): Sigmoid()
(7): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(8): FlattenLayer()
(9): Linear(in_features=256, out_features=120, bias=True)
(10): BatchNorm()
(11): Sigmoid()
(12): Linear(in_features=120, out_features=84, bias=True)
(13): BatchNorm()
(14): Sigmoid()
(15): Linear(in_features=84, out_features=10, bias=True)
)
#batch_size = 256
##cpu要调小batchsize
batch_size=16
def load_data_fashion_mnist(batch_size, resize=None, root='/home/kesci/input/FashionMNIST2065'):
"""Download the fashion mnist dataset and then load into memory."""
trans = [] if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=2)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=2)
return train_iter, test_iter
train_iter, test_iter = load_data_fashion_mnist(batch_size)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
简洁实现
简洁实现
#调用nn.BatchNorm2d(通道数):卷积层后面的bn；nn.BatchNorm1d(输出神经元个数):全连接层后面的bn
net = nn.Sequential(
nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
nn.BatchNorm2d(6),
nn.Sigmoid(),
nn.MaxPool2d(2, 2), # kernel_size, stride
nn.Conv2d(6, 16, 5),
nn.BatchNorm2d(16),
nn.Sigmoid(),
nn.MaxPool2d(2, 2),
d2l.FlattenLayer(),
nn.Linear(16*4*4, 120),
nn.BatchNorm1d(120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.BatchNorm1d(84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
残差网络（ResNet））
残差网络（
深度学习的问题：深度CNN网络达到一定深度后再一味地增加层数并不能带来进一步地分类性能提高，反而会招致网络收敛变得更慢，准确率也变得
更差。
残差块（Residual Block））
残差块（
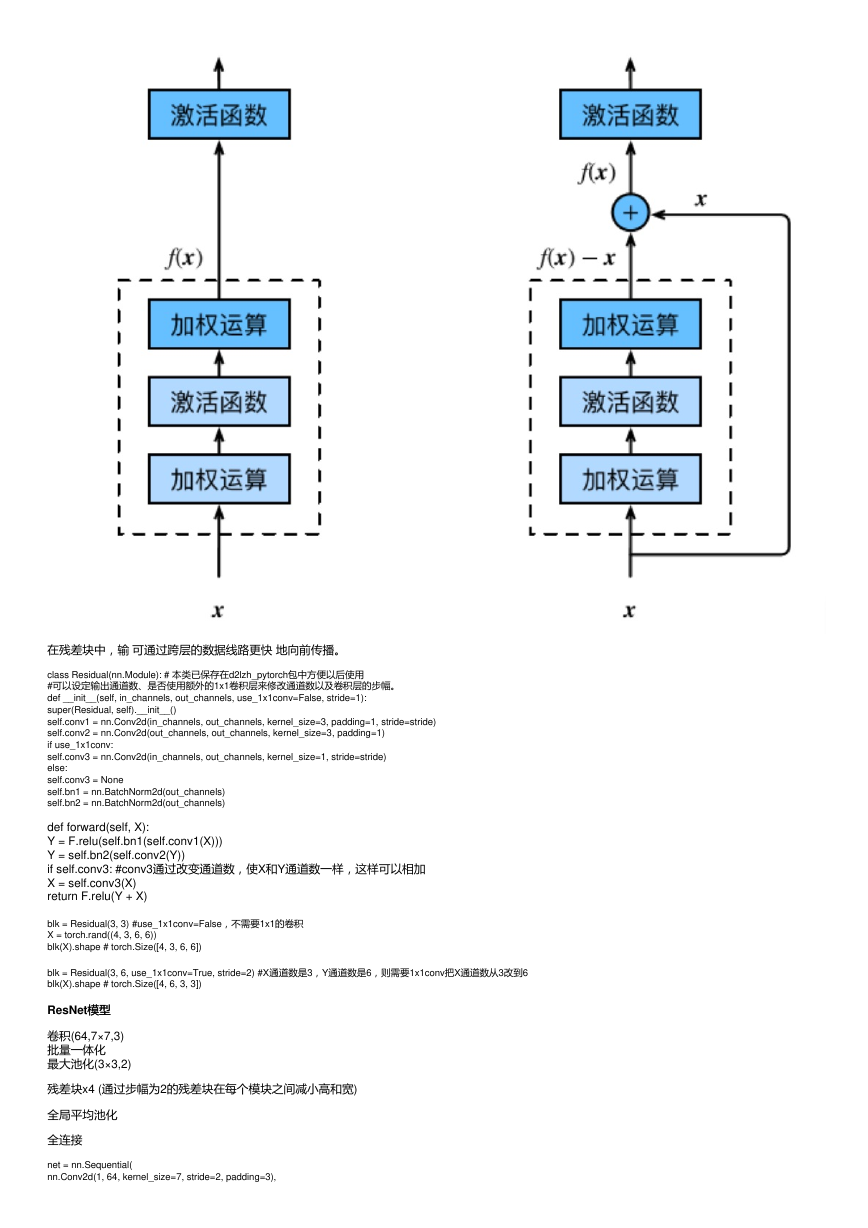
恒等映射：
左边：f(x)=x
右边：f(x)-x=0 （易于捕捉恒等映射的细微波动）
在残差块中，输 可通过跨层的数据线路更快 地向前传播。
class Residual(nn.Module): # 本类已保存在d2lzh_pytorch包中方便以后使用
#可以设定输出通道数、是否使用额外的1x1卷积层来修改通道数以及卷积层的步幅。
def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
super(Residual, self).__init__()
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(out_channels)
self.bn2 = nn.BatchNorm2d(out_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3: #conv3通过改变通道数，使X和Y通道数一样，这样可以相加
X = self.conv3(X)
return F.relu(Y + X)
blk = Residual(3, 3) #use_1x1conv=False，不需要1x1的卷积
X = torch.rand((4, 3, 6, 6))
blk(X).shape # torch.Size([4, 3, 6, 6])
blk = Residual(3, 6, use_1x1conv=True, stride=2) #X通道数是3，Y通道数是6，则需要1x1conv把X通道数从3改到6
blk(X).shape # torch.Size([4, 6, 3, 3])
ResNet模型模型
卷积(64,7×7,3)
批量一体化
最大池化(3×3,2)
残差块x4 (通过步幅为2的残差块在每个模块之间减小高和宽)
全局平均池化
全连接
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(in_channels, out_channels, num_residuals, first_block=False):
# num_residuals：resnet_block里需要包含的残差块
if first_block:
assert in_channels == out_channels # 第一个模块的通道数同输入通道数一致
blk = [] for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(in_channels, out_channels, use_1x1conv=True, stride=2))
else:
blk.append(Residual(out_channels, out_channels))
return nn.Sequential(*blk)
net.add_module("resnet_block1", resnet_block(64, 64, 2, first_block=True))
net.add_module("resnet_block2", resnet_block(64, 128, 2))
net.add_module("resnet_block3", resnet_block(128, 256, 2))
net.add_module("resnet_block4", resnet_block(256, 512, 2))
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, 512, 1, 1) #全局平均池化
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(512, 10))) #全连接层
X = torch.rand((1, 1, 224, 224))
for name, layer in net.named_children():
X = layer(X)
print(name, ' output shape:\t', X.shape)
0 output shape: torch.Size([1, 64, 112, 112])
1 output shape: torch.Size([1, 64, 112, 112])
2 output shape: torch.Size([1, 64, 112, 112])
3 output shape: torch.Size([1, 64, 56, 56])
resnet_block1 output shape: torch.Size([1, 64, 56, 56])
resnet_block2 output shape: torch.Size([1, 128, 28, 28])
resnet_block3 output shape: torch.Size([1, 256, 14, 14])
resnet_block4 output shape: torch.Size([1, 512, 7, 7])
global_avg_pool output shape: torch.Size([1, 512, 1, 1])
fc output shape: torch.Size([1, 10])
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
稠密连接网络（DenseNet））
稠密连接网络（
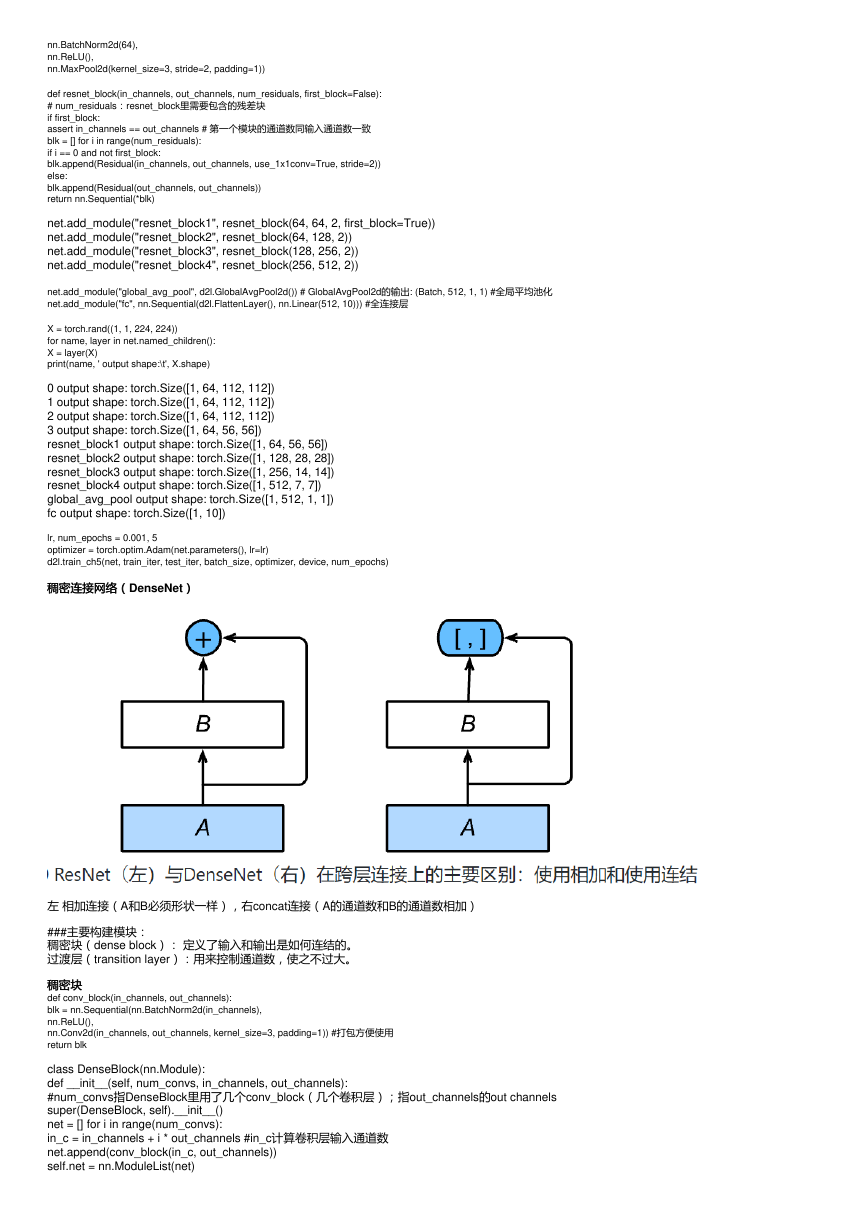
左 相加连接（A和B必须形状一样），右concat连接（A的通道数和B的通道数相加）
###主要构建模块：
稠密块（dense block）： 定义了输入和输出是如何连结的。
过渡层（transition layer）：用来控制通道数，使之不过大。
稠密块稠密块
def conv_block(in_channels, out_channels):
blk = nn.Sequential(nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)) #打包方便使用
return blk
class DenseBlock(nn.Module):
def __init__(self, num_convs, in_channels, out_channels):
#num_convs指DenseBlock里用了几个conv_block（几个卷积层）；指out_channels的out channels
super(DenseBlock, self).__init__()
net = [] for i in range(num_convs):
in_c = in_channels + i * out_channels #in_c计算卷积层输入通道数
net.append(conv_block(in_c, out_channels))
self.net = nn.ModuleList(net)
self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数
def forward(self, X):
for blk in self.net:
Y = blk(X) # X经过卷积层
X = torch.cat((X, Y), dim=1) # 在通道维上将输入和输出连结
return X
blk = DenseBlock(2, 3, 10) #23=3+2*10
X = torch.rand(4, 3, 8, 8)
Y = blk(X)
Y.shape # torch.Size([4, 23, 8, 8])
过渡层过渡层
PS：稠密块的使用会使模型通道数越来越多，过渡层用来减小模型复杂度
1×11\times11×1卷积层：来减小通道数
步幅为2的平均池化层：减半高和宽
def transition_block(in_channels, out_channels):
blk = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, out_channels, kernel_size=1), #1x1卷积层
nn.AvgPool2d(kernel_size=2, stride=2)) #步幅为2平均池化层
return blk
blk = transition_block(23, 10) #输入23，输出是需要放缩到的大小 10
blk(Y).shape # torch.Size([4, 10, 4, 4])
DenseNet模型模型
net = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), #[1, 64, 48, 48] nn.BatchNorm2d(64), #不改变形状[1, 64, 48, 48] nn.ReLU(), #不改变形状[1, 64, 48, 48]
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)) #[1, 64, 24, 24]
num_channels, growth_rate = 64, 32
# num_channels为当前的通道数，growth_rate 相当于前面定义的每经过一个卷积层增长的outchannels
num_convs_in_dense_blocks = [4, 4, 4, 4] #每个稠密块四层卷积
#结构：稠密块-过渡层-稠密块-过渡层-稠密块-过渡层-稠密块-过渡层
for i, num_convs in enumerate(num_convs_in_dense_blocks):
DB = DenseBlock(num_convs, num_channels, growth_rate)
net.add_module("DenseBlosk_%d" % i, DB)
# 上一个稠密块的输出通道数
num_channels = DB.out_channels #稠密块后：192=64+4*32
# 在稠密块之间加入通道数减半的过渡层
if i != len(num_convs_in_dense_blocks) - 1:
net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2)) #过渡块后：96
num_channels = num_channels // 2
net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(num_channels, 10)))
X = torch.rand((1, 1, 96, 96))
for name, layer in net.named_children():
X = layer(X)
print(name, ' output shape:\t', X.shape)
0 output shape: torch.Size([1, 64, 48, 48])
1 output shape: torch.Size([1, 64, 48, 48])
2 output shape: torch.Size([1, 64, 48, 48])
3 output shape: torch.Size([1, 64, 24, 24])
DenseBlosk_0 output shape: torch.Size([1, 192, 24, 24])
transition_block_0 output shape: torch.Size([1, 96, 12, 12])
DenseBlosk_1 output shape: torch.Size([1, 224, 12, 12])
transition_block_1 output shape: torch.Size([1, 112, 6, 6])
DenseBlosk_2 output shape: torch.Size([1, 240, 6, 6])
transition_block_2 output shape: torch.Size([1, 120, 3, 3])
DenseBlosk_3 output shape: torch.Size([1, 248, 3, 3])
BN output shape: torch.Size([1, 248, 3, 3])
relu output shape: torch.Size([1, 248, 3, 3])
global_avg_pool output shape: torch.Size([1, 248, 1, 1])
fc output shape: torch.Size([1, 10])
#batch_size = 256
batch_size=16
# 如出现“out of memory”的报错信息，可减小batch_size或resize
train_iter, test_iter =load_data_fashion_mnist(batch_size, resize=96)
lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)
习题习题
nn.BatchNorm2d(6)的含义是 d
全连接层的批量归一化，batchsize为6
卷积层的批量归一化，batchsize为6
全连接层的批量归一化，输出神经元个数为6
卷积层的批量归一化，通道数为6
答案解释
答案解释
选项四：正确，nn.BatchNorm2d()表示卷积层的BN，参数为通道数。nn.BatchNorm1d()表示全连接层的BN，参数为输出神经元个数。
关于BN层描述错误的是 b
卷积层的BN位于卷积计算之后，激活函数之前。
拉伸参数和偏移参数均为超参数。
预测时用移动平均估算整个训练数据集的样本均值和方差。
BN层能使整个神经网络在各层的中间输出的数值更稳定。
答案解释
答案解释
选项2：错误，拉伸参数和偏移参数为可学习参数。
关于ResNet描述错误的是 c
残差网络由多个残差块组成。
在残差块中，输 可通过跨层的数据线路更快地向前传播。
可以通过不断加深网络层数来提高分类性能。
较普通网络而言，残差网络在网络较深时能更好的收敛。
答案解释
答案解释
选项3：错误，网络达到一定深度后再一味地增加层数反而会招致网络收敛变得更慢，准确率也变得更差。
稠密连接网络过渡层中，1*1卷积层的主要作用是 a
减小通道数
增加通道数
引入非线性
代替全连接层
在稠密块中，假设由3个输出通道数为8的卷积层组成，稠密块的输入通道数是3，那么稠密块的输出通道数是 d
8
11
24
27
答案解释 输出通道数=输入通道数+卷积层个数*卷积输出通道数
答案解释
作者：weixin_42314414
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
