第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
已实现波动率模型和传统波动率模型的波动率预测能力的比较.pdf
中国科技论文在线
http://www.paper.edu.cn
已实现波动率模型和传统波动率模型的波
动率预测能力的比较
王阳，雷钦礼**
（暨南大学经济学院，广州 510632）
摘要：本文以沪深 300 指数为例，将基于其 5 分钟高频数据的已实现波动率模型和基于其日
收益数据的历史波动率模型这两类波动率模型的样本外日波动率的预测能力进行比较。结果
发现，无论是样本内预测还是样本外预测，已实现波动率模型比传统的 EGARCH 模型有更
好的预测能力；把已实现波动率作为解释变量加入传统的 EGARCH 模型的方差模型之后，
有助于提高模型对数据的拟合能力和预测能力。
关键词：已实现波动率；波动率模型；高频数据；波动率预测
中图分类号：F830.9
Comparison of volatility forecasting capabilities of realized
volatility model and traditional volatility model
WANG Yang, LEI Qinli
(Economics School, Jinan University, Guangzhou 510632)
Abstract: Taking the Shanghai and Shenzhen 300 Index as an example, the forecasting ability of
the volatility model based on the 5-minute high-frequency data and the historical volatility model
based on the daily return data Comparison. It is found that the realized volatility model has better
prediction ability than the traditional EGARCH model both in intra-sample prediction and
out-of-sample prediction. After adding the realized volatility as the explanatory variable to the
variance model of the traditional EGARCH model, To improve the model's ability to fit the data
and predictive ability.
Key words: realized volatility; volatility model; high-frequency data; volatility prediction
0 引言
在金融市场中，作为资产收益率的波动性即波动率是金融研究中的一个非常重要的变
量，无论是金融产品的投资组合、风险管理还是资产定价，波动率都扮演着至关重要的角色。
如何对波动率进行精确的刻画与预测是金融学领域关注的焦点之一。分析收益波动率的特性
及走向，对投资者度量和规避市场风险均有重要的研究价值和实际意义。
目前对金融资产波动率的模型描述方法主要有以下三种类型：第一类是历史波动率模型
( historical volatility model)的描述方法，这类波动率模型的构建基于历史收益数据，并且这
些历史收益数据的时间一般较长，通常为每日、每周甚至是每月。这类模型中比较有代表性
的便是 Engle(1982)的自回归条件异方差模型(ARCH) [1]、Bollerslev(1986)的广义自回归条件
异方差模型(GARCH) [2]以及 Taylor(1986)的随机波动模型(SV) [3]；第二类是隐含波动率模型
(impliedvolatility model)，应用期权市场上的价格，通过某个定价公式(如 B-S 定价公式)来推
导资产的波动率；第三类是已实现波动率模型(realized volatility model)。因为传统上的用日
收益率的平方作为日波动率的测度将会面临非常严重的测量误差和噪声，而使用基于交易日
作者简介：王阳（1990-），男，硕士研究生，主要研究方向：宏观经济计量方法
通信联系人：雷钦礼（1956-），男，暨南大学经济学院教授，博士生导师，主要研究方向：经济增长与波
动分析. E-mail: tlqli@jnu.edu.cn
- 1 -
5
10
15
20
25
30
35
40
中国科技论文在线
http://www.paper.edu.cn
内高频收益数据的已实现波动率(RV)作为日波动率的测度，将大大降低这些误差和噪声对真
实的、潜在的波动率过程的影响。
由于隐含波动率是建立在某些关联期权价格和它相应的股票价格的假定上，所以这种方
法往往由于它的模型的相依性而遭到批评，故此类模型本文不予考虑。自单一的 GARCH 模
型被提出以来逐渐深化发展成 GARCH 族，一直广泛运用于经济、金融等诸多领域。这些
GARCH 族模型均能很好的刻画收益率的波动过程，且相比于其他事变的波动模型(比如 SV
模型)，GARCH 族模型具有形式简洁、参数易估计的优势，因此本文也不予考虑 SV 模型。
不少学者在 GARCH 族模型的预测方面做了研究。方立兵等[4]用 EF 方法对十类常见的
GARCH 模型进行预测能力的比较，发现 EGARCH 模型有相对较好的预测能力；刘青等[5]
采用最小二乘方法进行模型预测能力对比，也得出类似结果。方立兵等[6]运用蒙特卡洛模拟
考察十类 GARCH 模型分别在正态分布、t 分布、GED 以及偏斜-t 分布假设下的波动率预测
能力，结果发现偏斜-t 分布下的 GARCH 族模型有更好的预测能力。然而，GARCH 族模型
是使用低频收益率的数据来预测未来的波动率，无法考虑日内交易信息。随着高频数据的越
来越方便获得，便有了一些新的方法和模型对资产波动率的更加精确的预测。Andersen and
Bollerslev[7]首次提出 RV 作为资产收益率的一致非参数估计量，该估计量具有无偏性和较好
稳健性。魏宇[8]利用沪深 300 股指期货数据将已实现波动率模型与传统的 GARCH 模型以及
SV 模型的预测能力进行了比较。吴有英等[9]利用沪深 300 指数的 RV 序列建立 ARFIMA 模
型并预测。
以上研究很少有已实现波动率模型和 GARCH 族模型的预测能力比较，即使有也只是与
最简单的 GARCH(1,1)作比较，并没有考虑具有较优预测能力的 EGARCH 模型，也没有考
虑除正态分布外的其他分布假设下的模型预测能力。鉴于此，本文将采用沪深 300 指数 5
分钟交易数据和日收益数据，全面比较已实现波动率模型和 EGARCH 模型之间的预测能力。
与前人研究不同之处主要有：第一，将已实现波动率模型与具有较优预测能力的 EGARCH
模型进行波动率的预测能力比较；第二，考虑在传统的 EGARCH 的方差方程中加入额外的
解释变量 RV，建立 EGARCH-RV 模型，并考虑在不同分布假设下，与已实现波动率模型的
波动率预测能力进行比较。
1 数据说明、已实现波动率的估计
1.1 数据说明
本文研究的数据样本为沪深 300 指数的 5 分钟高频数据和日数据（来自 Wind 数据库），
=
rt
(
100* ln
时间从 2012 年 11 月 6 日到 2013 年 12 月 31 日，共 N=278 个交易日。日收益率计算方式
，其中 tc 是第 t(t=1,…,277)
使用常用的“收盘价—收盘价”收益率，即
天的收盘价格，这样由全部样本可以得到 277 个收益率数据。对于 5 分钟高频数据，每天有
4 个小时交易时间，因此每个交易日可以记录 48 个 5 分钟高频数据，全部样本合计 13296
个 5 分钟高频数据，则第 t 天内的高频收益率可表示为
,t dc 是第 t 天中第 d(d=1,…,48)个 5 分钟交易数据的收盘价格。
(
100* ln
，其中
ln
c
t
ln
c
t d
,
c
t
+
1
c
t
+
1,
d
rtd
=
−
)
−
)
1.2 已实现波动率的估计
根据 Andersen and Bollerslev(1998)[7]的定义，第 t 天的已实现波动率的估计可表示为第
- 2 -
45
50
55
60
65
70
75
中国科技论文在线
http://www.paper.edu.cn
t 天内所有高频收益率的平方和，即
RV
t
= 。但是，这种估计方法只能反映交易时
rtd
2
48
d
=
1
80
间内的波动状况，无法反映非交易时间段的波动状况。为使已实现波动率的估计全面真实地
反映波动状况，Hansen and Lunde(2006) [10]用尺度参数δ来对 tRV 进行尺度变换，即第 t 天
的已实现波动率的估计为：
RV
RVδ=
t
*
δ
=
，
2
rt
，其中 N 表示收益率的个数。
1
−
N
N
=
t
1
N
=
1
t
−
1
N
RV
t
这样，日收益率 rt 、日收益率的平方 2rt 以及已实现的波动率 RV 的一些描述性统计由
表 1 给出：
85
表 1 日收益率、日收益率的平方以及已实现的波动率的一些描述性统计
Tab. 1 The descriptive statistics of daily rate of return, the square of the daily rate of return and the
realization of the volatility
日收益率相关系列
2rt
0.03272335
0.07284983
6.9928036
68.93122
已实现波动率序列
RV
0.03272335
0.0310823
6.478592
60.25303
rt
-9.99511E-05
0.18122335
-0.0656595
2.895284
99.8326 ***
mean
sd
skewness
kurtosis
J-B
Q(4)
Q(8)
Q(12)
注：“***”表示 5%的水平上显著，其中 kurtosis 为超额峰态，J-B 为 Jarque-Bera 统计量，Q(n)为滞后 n
44501.1264 ***
43.4519 ***
52.7531 ***
58.7761 ***
0.3893
10.3271
11.3434
0.2093
0.2136
0.4681
57956.5535 ***
阶的 Ljung-Box 统计量。
90
95
由表 1 可以看出，收益率平方的均值与 RV 的均值相等，但后者的标准差比前者小；三
者都呈现“尖峰厚尾”特征，不满足正态特征，表明沪深 300 指数波动幅度较为剧烈；收益率
和收益率的平方没有显著的序列相关性，但是 RV 具有非常显著的序列相关性，表明沪深
300 指数的波动率聚集特征和波动率的持续性特征。进一步地对 RV 序列进行 ADF 单位根
检验结果(滞后 12 阶的 DF 值为-3.2502)——拒绝存在单位根的原假设。因此可以认为各个序
列是平稳的，可以进一步的对各个序列建模。
2 各类波动率模型
2.1 已实现波动率模型
Andersen 等(2005) [11]研究指出，由于潜在的、真实的市场波动率是不可观测的，因此目
前公认的方法是用基于高频收益数据的已实现波动率估计来作为真实市场波动率的替代变
量和基准。
100
图 1 所示的是 RV 序列的自相关图和偏自相关图。从图中可以看出，RV 序列只有前 3
阶有显著的自相关，出现短暂的相关性。但与前人研究[12]不同的是，这里并没有出现所谓
的“长记忆”特征，原因可能是样本数据量少(只有 277 个数据)。另外，5 分钟的时间间隔可
能不是最优时间间隔。
- 3 -
中国科技论文在线
http://www.paper.edu.cn
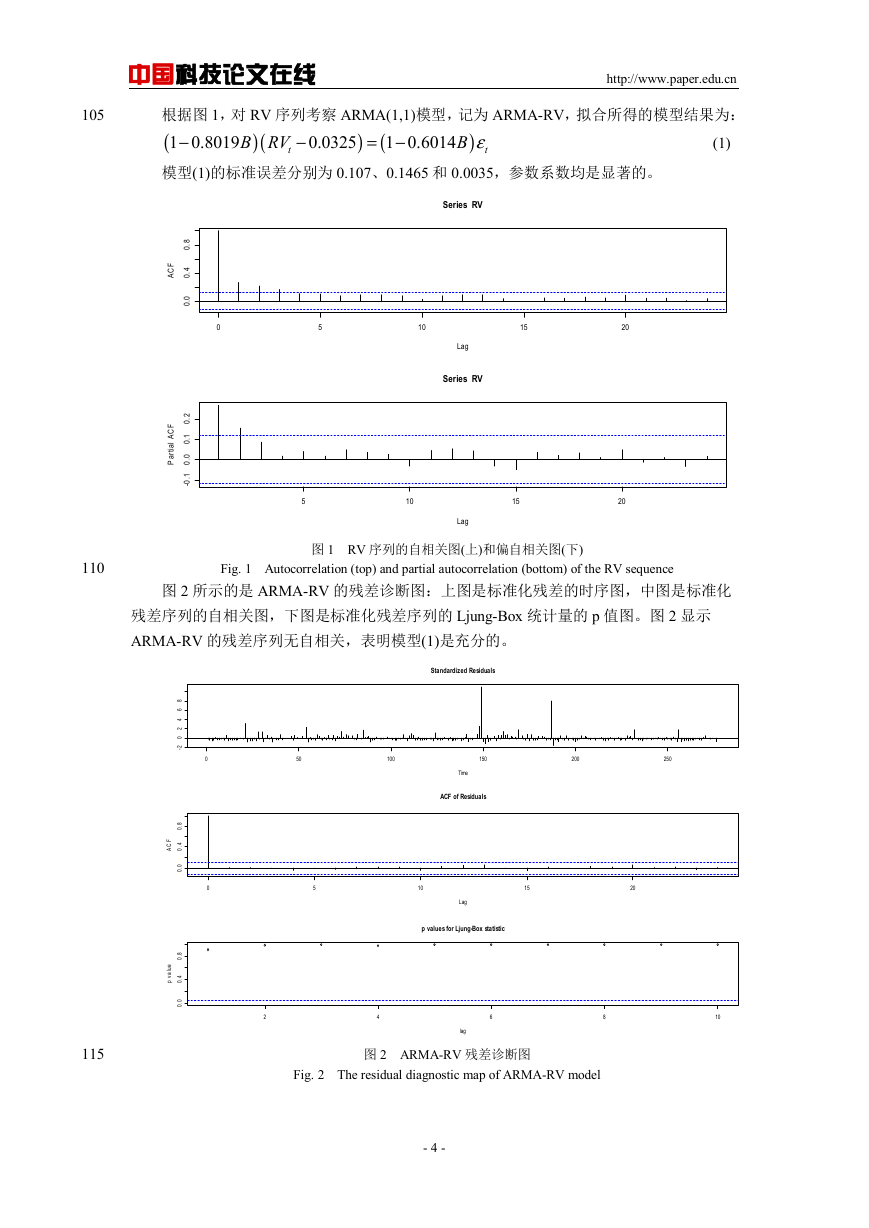
105
根据图 1，对 RV 序列考察 ARMA(1,1)模型，记为 ARMA-RV，拟合所得的模型结果为：
(
−
1 0.8019
模型(1)的标准误差分别为 0.107、0.1465 和 0.0035，参数系数均是显著的。
(1)
)(
B RV
t
)
(
= −
1 0.6014
)
B ε
t
−
0.0325
Series RV
0
5
10
15
20
Lag
Series RV
8
.
0
F
C
A
4
.
0
0
.
0
F
C
A
l
a
i
t
r
a
P
2
.
0
1
.
0
0
.
0
1
.
0
-
5
10
15
20
Lag
110
Fig. 1 Autocorrelation (top) and partial autocorrelation (bottom) of the RV sequence
图 1 RV 序列的自相关图(上)和偏自相关图(下)
图 2 所示的是 ARMA-RV 的残差诊断图：上图是标准化残差的时序图，中图是标准化
残差序列的自相关图，下图是标准化残差序列的 Ljung-Box 统计量的 p 值图。图 2 显示
ARMA-RV 的残差序列无自相关，表明模型(1)是充分的。
Standardized Residuals
0
0
8
6
4
2
0
2
-
8
.
0
F
C
A
4
.
0
0
.
0
e
u
l
a
v
p
8
.
0
4
.
0
0
.
0
50
100
150
Time
ACF of Residuals
200
250
5
10
15
20
Lag
p values for Ljung-Box statistic
2
4
6
lag
8
10
115
图 2 ARMA-RV 残差诊断图
Fig. 2 The residual diagnostic map of ARMA-RV model
- 4 -
中国科技论文在线
2.2 传统波动率模型
http://www.paper.edu.cn
由于 EGARCH 模型考虑了正的和负的资产收益率的非对称效应，因此相对
于其他的 GARCH 类模型有较优的预测能力[4]。根据 Nelson (1991) [13]的研究，
EGARCH 的一般形式可写为：
120
r
t
=
+
φ
0
p
=
1
i
φ
r
i
t
−
1
+
(
ln
)
σ α α
i
=
+
2
t
0
m
=
1
i
q
j
j
2
t
+
ϕσ ε
t
=
1
ε γε
−
t
t
−
i
i
+
σ
−
t
i
(
β σ
2
−
t
ln
j
(2)
)
j
i
+
s
=
1
j
为了增强已实现波动率模型和 EGARCH 模型预测能力的对比性，考虑将已实现波动率
RV 作为解释变量加入 EGARCH 的方差模型中，于是模型(2)可写为：
r
t
=
+
φ
0
p
=
1
i
φ
r
i
t
−
1
+
q
j
(
ln
)
σ α α
i
=
+
2
t
0
m
=
1
i
ϕσ ε
t
+
2
t
j
=
1
ε γε
−
t
t
−
i
i
+
σ
−
t
i
i
+
s
=
1
j
(
β σ θ
*
ln
+
2
−
t
j
j
)
(3)
RV
t
125
将模型(3)记为 EGARCH-RV，和模型(2)的 EGARCH 一样， tε独立同分布于正态分布。
当假设 tε独立同分布于偏斜-t 分布时，记模型(3)为 EGARCH-RV-st。
对日收益 rt 序列，考察三种模型形式，即 AR(5)-EGARCH(1,1)，AR(5)-EGARCH(1,1)-RV，
AR(5)-EGARCH(1,1)-RV-st，三种模型参数估计结果及模型的残差诊断由下表 2 所示：
130
ar1
ar2
ar3
ar4
ar5
omega
alpha1
beta1
gamma1
vxreg1
skew
shape
残差 Q(10)
残差 Q(20)
残差平方 Q(10)
残差平方 Q(20)
表 2 三种模型参数估计结果及模型残差诊断
Tab. 2 Estimation results of three model parameters and model residuals
AR(5)-EGARCH(1,1)
AR(5)-EGARCH(1,1)-RV
AR(5)-EGARCH(1,1)-RV-st
0.030788
-0.025146
0.028325
0.040513
-0.033592
-0.738678
-0.216778 ***
0.785374 ***
0.039858
11.7538
19.3109
11.9872
15.4588
0.011576
-0.044567
0.055872
0.03767 ***
-0.057851
-1.867274 ***
-0.15431 ***
0.558395 ***
-0.391871 ***
8.688174 ***
9.4391
14.6244
15.8697
27.1865
0.031692
-0.041291
0.057064 ***
0.048079 ***
-0.097602 ***
-1.970433 ***
-0.181968 ***
0.532178 ***
-0.459336 ***
9.450713 ***
1.360426 ***
8.254043 ***
11.584
16.3533
14.9308
27.1588
注：三种模型估计结果都是去掉均值方程的截距项后所得到的结果。“***”表示 5%的水平上显著，Q(n)
β，
1
为滞后 n 阶的 Ljung-Box 统计量。ar 表示模型(2)中的
α，beta1 表示
1
φ，omega 表示
j
α ，alpha1 表示
0
gamma1 表示
γ，vxreg 表示θ，skew 和 shape 分别是偏斜-t 分布的偏度和自由度。
1
由表 2 可以看出，三种模型残差序列无自相关，也没有 ARCH 效应，表明三种模型均
是充分的。方差方程加进 RV 之后有助于模型对波动率的刻画，同时当模型的误差分布服从
135
- 5 -
中国科技论文在线
偏斜-t 分布时能更好的拟合数据、描绘波动率。
3 预测能力比较
3.1 预测方法
http://www.paper.edu.cn
140
一般地，模型在进行样本外比较时，通常采用预测误差的均方(RMSE)和预测误差的平
均绝对值(MAE)这两个指标来量化模型的预测能力。为比较两类波动率模型的预测能力，这
里采用一步外推的回测检验。具体步骤如下：
1) 将数据集分割为估计子样本和预测子样本。这里将 rt 序列和 RV 序列均分为 200 个估计
子样本和 77 个预测子样本；
145
和它的预
2) 用估计子样本中的数据进行估计，利用拟合的模型得到超前一步预测和它的预测误差。
比如估计子样本是{
tx t
|
测误差 ( )
−
+=
x
x
1
h
h
e
h
1
,
}
h
= ，用前 h 个数据来计算超前一步预测 ( )1hx
1,
( )
1
；
3) 对估计子样本添加一个新的数据点，变为{
+
h
1,
估计模型，计算超前一步预测和它的预测误差，即 ( )
e
1
h
tx t
|
=
+
1
,
}
1
=
，再用前 h+1 个模型重新
x
h
( )
1
；
x
h
−
+
1
+
2
4) 重复步骤 3)，直到超前一步预测误差为
( )
1
=
e
N
−
1
x
N
−
x
N
−
1
( )
1
，N 是样本量。
150
那么，模型的 RMSE 和 MAE 分别为：
RMSE
=
N
−
1
=
j h
e
( )
21
j
−
N h
，
MAE
N
−
1
( )
1
e
==
j h
N h
j
−
。
3.2 预测结果
根据上述回测检验的步骤，分别计算前面四种波动率模型的 RMSE 和 MAE，计算结果
如表 3 所示：
155
表 3 四种波动率模型的预测能力
Tab. 3 Predictive capabilities of four volatility models
ARMA-RV
EGARCH
EGARCH-RV
EGARCH-RV-st
RMSE
0.01375413
0.2412006
0.2192107
0.2120246
MAE
0.01059139
0.2086846
0.1847816
0.1790988
由表 3 可以看出，ARMA-RV 的 RMSE 和 MAE 均远小于其他模型，表明 ARMA-RV
具有出色的预测能力。更一般地，已实现波动率模型比传统的 EGARCH 模型有较优的预测
能力。这一结果也表明，相对于日数据，高频数据中确实蕴含着更加丰富的市场波动信息。
另外，带偏斜-t 分布的、加入已实现波动率的、扩展的 EGARCH 模型的预测能力也不错；
普通的 EGARCH 的预测能力最弱；加入已实现波动率以后的 EGARCH 的预测能力有显著
的改进。
160
- 6 -
中国科技论文在线
4 结论
http://www.paper.edu.cn
165
170
本文以沪深 300 指数的 5 分钟交易数据和日交易数据为例，探讨了两类主流的波动率模
型对其样本外日波动率的预测能力，主要的实证结果显示：就沪深 300 指数而言，已实现波
动率模型的预测能力要高于传统的 EGARCH 模型。在所考察的预测能力的评价标准下，已
实现波动率模型均有较高的预测精度，而加入已实现波动率的扩展的 EGARCH 的模型的预
测能力对比普通的 EGARCH 模型有显著的改进。而在 GARCH 族模型中具有较优预测能力
的、常用的、普通的 EGARCH 模型的预测能力并不令人满意。因此,对于在成熟资本市场适
用的金融理论和模型，必须进行认真的比较和检验，才能判定其是否也适合我国新兴资本市
场的实际情况。
此外，本文的研究方法和结论对构建我国金融机构的风险管理系统和准确度量资产价
格，都具有重要的理论和现实意义。当然，如何对研究中的一些与成熟资本市场结论不相吻
合的实证结果进行理论解释，并进一步寻找更加适合中国资本市场实际风险状况和波动特征
的波动率模型，仍然是下一步研究的主要方向。
175
[参考文献] (References)
180
185
190
195
200
[1] Engle R F. Autoregressive Conditional Heteroskedasticity with Estimates of the variance of UK inflation[J].
Econometrica, 1982, 50(3): 987-1007.
[2] Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of Econometrics, 1986,
31(2): 307-327.
[3] Taylor S J. Modeling Financial Time Series[M]. Chichester: John Wiley and Sons, 1986.
[4] 方立兵，郭炳伸，曾勇．GARCH 族模型的预测能力比较：一种半参数方法[J]．数量经济技术经济研究，
2010，4：148-159.
[5] 刘青，戴经跃，杨超．基于 GARCH 族模型的收益波动率预测绩效评估方法[J]．统计与决策，2015，9：
160-163.
[6] 方立兵，郭炳伸，曾勇．偏斜参数对 GACH 族模型估计与预测绩效的影响[J]．统计研究，2014，31(10)：
107-112.
[7] Andersen T G, Bollerslev T. Answering the skeptics: Yes, standard volatility models do provide accurate
forecasts [J]. International Economic Review, 1998, 39(6): 885-905.
[8] 魏宇. 沪深 300 股指期货的波动率预测模型研究[J]. 管理科学学报，2010，13(2)：66-76.
[9] 吴有英，马玉林，赵静. 基于"已实现"波动率的 ARFIMA 模型预测实证研究[J]. 投资研究，2011，30(10)：
153-159.
[10] Hansen P R, Lunde A. Consistent ranking of volatility models [J]. Journal of Econometrics, 2006, 131(6):
97-121.
[11] Andersen T G, Bollerslev T, Meddahi N. Correcting the errors: Volatility forecast evaluation using high
frequency data and realized volatilities [J]. Econometrica, 2005, 73(1): 279 -296.
[12] Andersen T G, Bollerslev T. The Distribution of Stock Return Volatility [J]. Journal of Financial Economic,
2001, 61: 43-76.
[13] Nelson D B. Conditional heteroskedasticity in asset returns: A new approach [J]. Econometrica, 1991, 59(2):
347–370.
- 7 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
