正规式到正规文法的算法实现.doc-资料库

baoqing87625-1416430-4744302543316794591.doc.pdf-第1页.png

第1页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第2页.png

第2页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第3页.png

第3页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第4页.png

第4页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第5页.png

第5页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第6页.png

第6页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第7页.png

第7页 / 共23页

baoqing87625-1416430-4744302543316794591.doc.pdf-第8页.png

第8页 / 共23页

湖南人文科技学院计算机系课程设计说明书课程名称: 《编译原理》课程代码: 题目: 正规式转化成 NFA 年级/专业/班:04 级计算机科学与技术专业计本二班学生姓名: 许湘宁、周坤华、李想、黄凯学号: 03 、 16 、 28 、41 指导教师: 羊四清开题时间: 2007 年 6 月 10 日完成时间: 2007 年 6 月 25 日

目录摘要……………………………………………………………………………………1 一、引言………………………………………………………………………………2 二、设计任务与目的 …………………………………………………………………4 三、设计方案与实施…………………………………………………………………5 1、总体设计 2、详细设计 3、程序清单 4、程序调试与体会 5、运行结果（截图）四、结论………………………………………………………………………………15 五、致谢………………………………………………………………………………15 六、参考文献…………………………………………………………………………15 摘要

一般的高级语言转化成机器语言都要经过词法分析、语法分析、语义分析、中间代码的生成与目标代码的生成。其中，在词法分析环节中可以用 LEX 等语言来自动进行词法分析，在其分析过程中，要用到正规式、DFA 与 NFA 之间的互相转化的过程。本课程设计从理论和实践上分析和实现正规式到 NFA 转化的方法及其 C 程序实现。关键词：正规式、确定化有限自动状态机、非确定的有限自动状态机 Abstract Key words: RegularExpression，NFA，DFA。 The generally deluxe language conversion becomes the machine languages to all want code through the phrase method analysis, phrasing analysis, the language righteousness analysis and in the center of born with the target code of born.Among them, can come from move to carry on the phrase method analysis with LEX etc. language in the phrase method analytical link, in its analytical process, want to use the process of the regular type, DFA and mutual conversion between NFA.This course design analyzes and carries out method and its C procedure realizations that regular type to NFA convert up from the theories and fulfillments. 《编译原理》课程设计

——正规式转化成 NFA 一、引言编程语言是由一个个句子构成的，而句子是由一个个单词构成的，因此单词是构成程序语言的基本单位。词法就是单词的构成法则，用这些法则来检查程序的单词构成是否合乎词法规则。进行词法分析的形式化工具目前主要有正规式、DFA 与 NFA，而且正规式、DFA、 NFA 在表现能力上是等价的，可以互相转化。正规式是一种形式化表达，而 DFA 和 NFA 是一种图形化的表达。二、设计目的与任务因为在词法分析时为了分析的方便我们有时要用到正规式，有时要用到 DFA，而有时可能还要用到 NFA。这三种工具在词法分析时互相参照，互相补充。词法分析器的自动产生语言 LEX 编译器的工作过程是首先根据正规式产生出 NFA，再由 NFA 构造出 DFA，再来产生我们的词法分析器。因此，我们设计的目的是来模仿其中的一个步骤，设计的任务是根据不同的输入正规式转化成 NFA 的形式输出，输出形式为 M={S0，S，&, $, F }五元式的形式。三、设计方案 1、总体设计（1）首先把屏幕上的一个正规式读入到一个缓冲区中保存起来，以便以后对正规式的分析与处理。（2）对正规式进行预处理，去掉里面的一些对分析不起作用的控制字符，为以后的分析与处理带来方便。（3）对字符串进行从左到右的分析与处理，这是最主要的一步，而在这一个模块里面又调用了几个功能模块，由正规式化成 NFA 主要就在这上步里完成。（4）构造状态转换矩阵，用于最后的映射函数的输出，此模块被第（3）个模块调用。（5）输出 NFA，以五元式的形式输出。以下为总体设计的层次图：主模块 Main 函数输入正规式的预处理分析与处理输出正规式构造状态矩阵 2、详细设计第一个模块设计理论为：从屏幕把正规式读入一个数组中。第二个模块的设计理论为：设置一个整型的指针，从数组的左边依次扫描到数组的右边，对分析正规式不产生影响的字符就去掉，只留下对正规式的分析起作用的字符串。把处理好的正规式存储在原数组中。

第三个模块的设计理论为：对数组里的正规式进行从左到右的扫描，在扫描的过程中如果遇到的字符为‘（’，就说明 NFA 的状态图产生了分支，就要进行对用括号括起来的字符串进行处理，直到遇到右括号为此。当遇到一个字符就调用构造状态矩阵的函数，对新产生的状态进行存储。第四个模块的设计理论为：对调用到此模块的函数传入的字符，首先判断其字符是否在字符集中，如果在，就只添加状态。如果不在，就要同时进行状态的添加与字符添加到字符集中。第五个模块的设计理论为：前面的功能模块对 NFA 的正规式的所有元素都已构造好了，此模块的功能为输出 NFA 的五元式的各元素，字符集，状态集，初态集，终态集都已保存在乐数组中，只要对每个数组进行循环的输出即可。而状态之间的转化关系保储在状态转换矩阵中，是一个二维的数组。我只要以这个二维的数组作为行，以字符集数组的下标作为例。即可把映射函数输出来。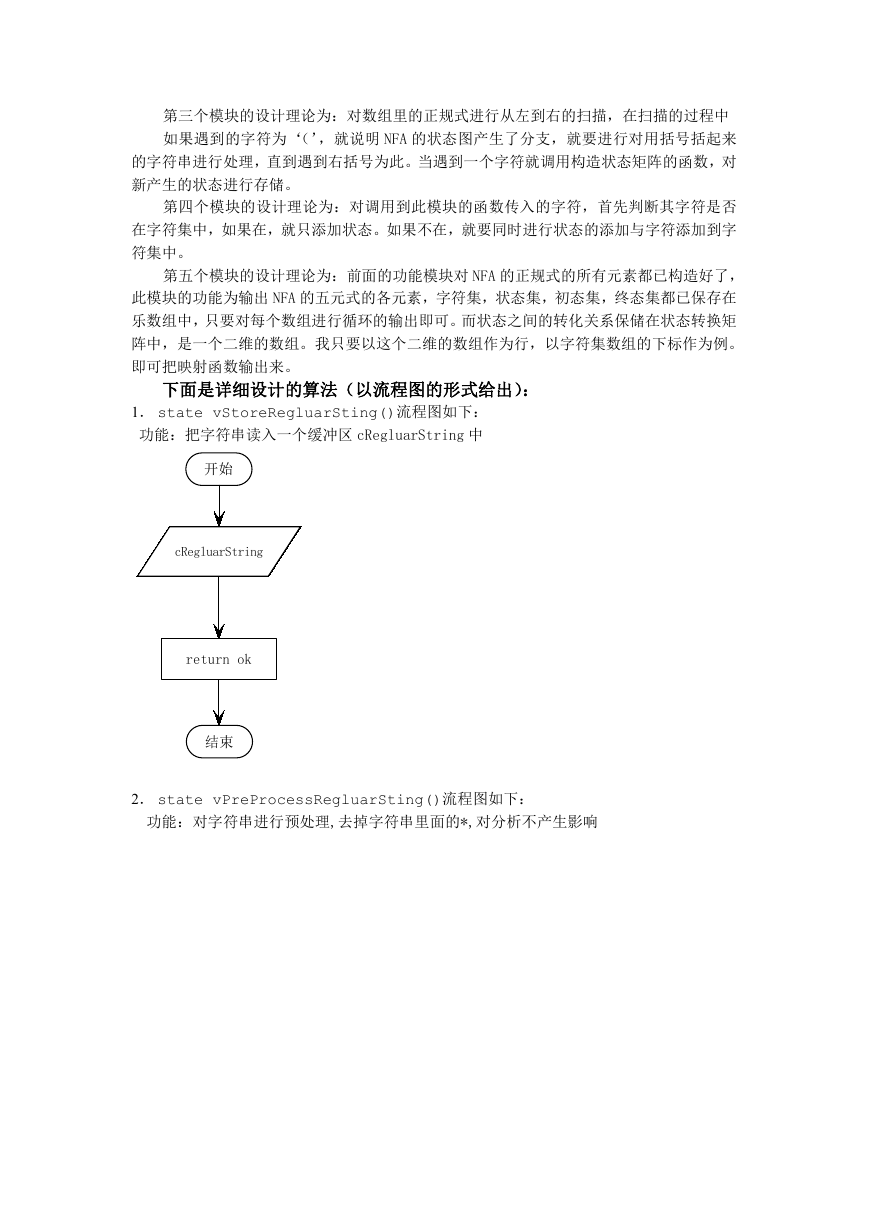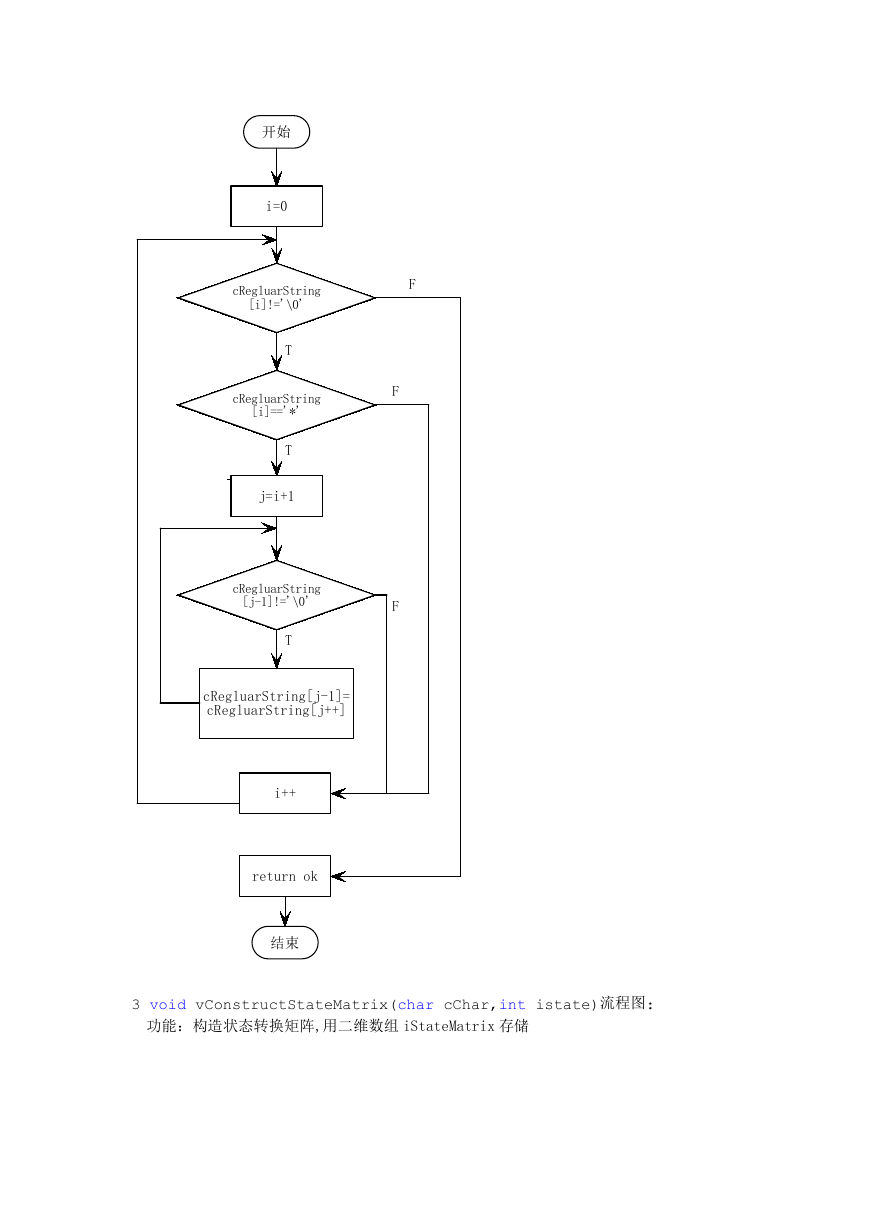下面是详细设计的算法（以流程图的形式给出）： 1． state vStoreRegluarSting()流程图如下：功能：把字符串读入一个缓冲区 cRegluarString 中开始 cRegluarString return ok 结束 2． state vPreProcessRegluarSting()流程图如下：功能：对字符串进行预处理,去掉字符串里面的*,对分析不产生影响

开始 i=0 cRegluarString [i]!='\0' F T cRegluarString [i]=='*' T j=i+1 cRegluarString [j-1]!='\0' T F F cRegluarString[j-1]= cRegluarString[j++] i++ return ok 结束 3 void vConstructStateMatrix(char cChar,int istate)流程图: 功能：构造状态转换矩阵,用二维数组 iStateMatrix 存储

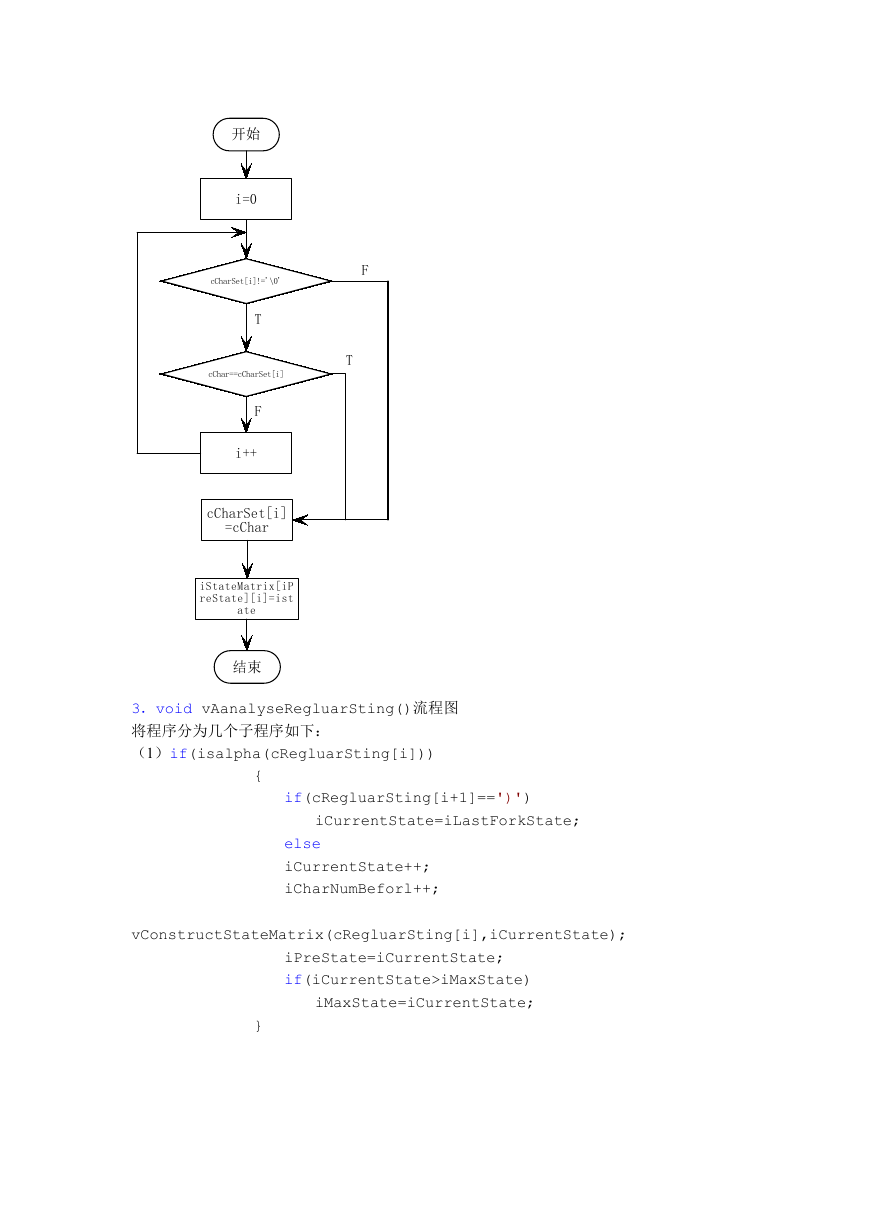
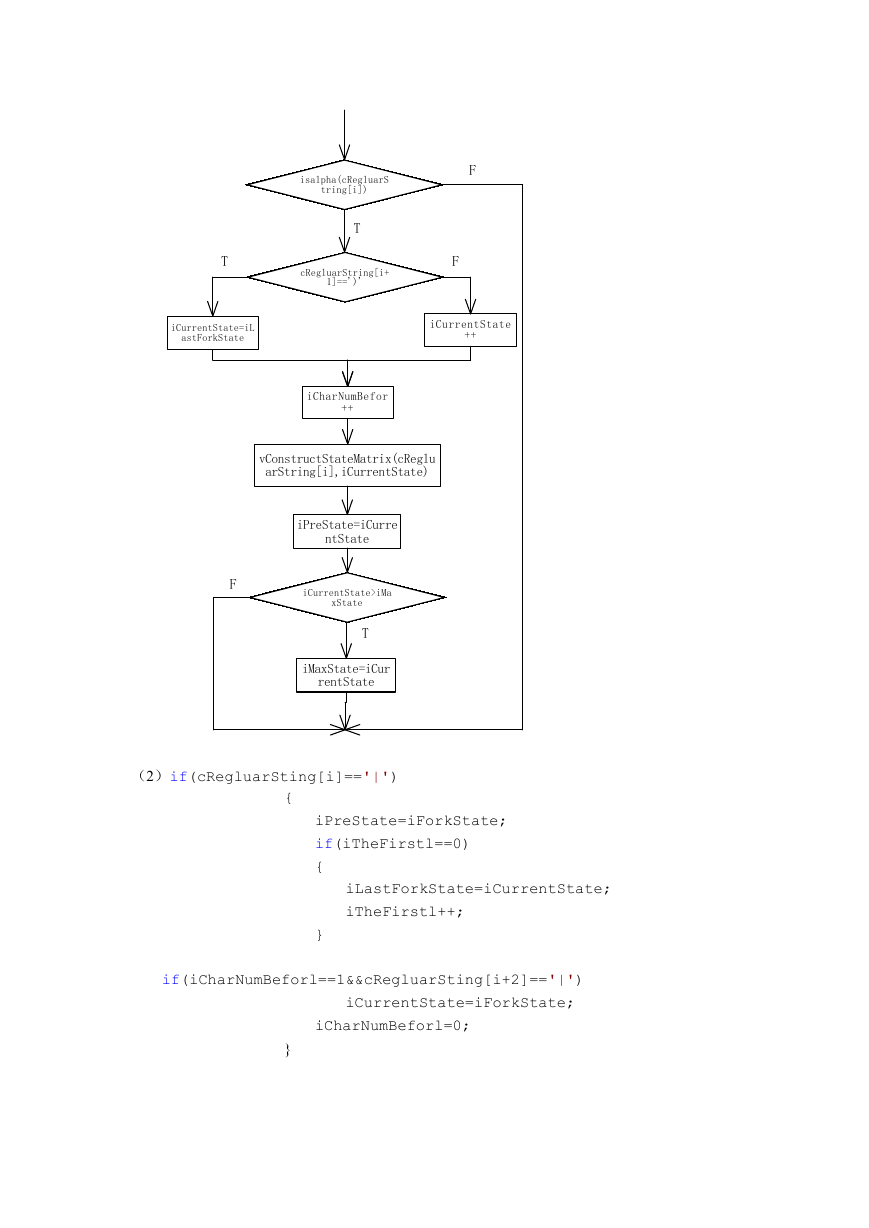
F T 开始 i=0 cCharSet[i]!='\0' T cChar==cCharSet[i] F i++ cCharSet[i] =cChar iStateMatrix[iP reState][i]=ist ate 结束 { } 3．void vAanalyseRegluarSting()流程图将程序分为几个子程序如下：（1）if(isalpha(cRegluarSting[i])) if(cRegluarSting[i+1]==')') iCurrentState=iLastForkState; else iCurrentState++; iCharNumBeforl++; iPreState=iCurrentState; if(iCurrentState>iMaxState) iMaxState=iCurrentState; vConstructStateMatrix(cRegluarSting[i],iCurrentState);

isalpha(cRegluarS tring[i]) T cRegluarString[i+ 1]==')' T F F iCurrentState=iL astForkState iCurrentState ++ iCharNumBefor ++ vConstructStateMatrix(cReglu arString[i],iCurrentState) F iPreState=iCurre ntState iCurrentState>iMa xState T iMaxState=iCur rentState （2）if(cRegluarSting[i]=='|') { } iPreState=iForkState; if(iTheFirstl==0) { iLastForkState=iCurrentState; iTheFirstl++; } if(iCharNumBeforl==1&&cRegluarSting[i+2]=='|') iCurrentState=iForkState; iCharNumBeforl=0;

资料库

正规式到正规文法的算法实现.doc

相关推荐

开发技术

热门标签

最新资料