logo资料库

Kmeans.docx K均值聚类算法实验报告

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：0.84M 资料格式：docx 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    实验4 K均值聚类算法
    1 实验目的
    2 实验环境
    3 实验原理
    4 实验内容
    5 实验小结
    模式识别实验报告 学号： 姓名： 日期：
    实验 4 K 均值聚类算法 1 实验目的 1.理解掌握 K-means 聚类算法的基本原理； 2.学会用 python 实现 K-means 算法 2 实验环境 Windows 10，Python 3.7.4，PyCharm 2019.2.3 3 实验原理 3.1 聚类简介 俗话说：“物以类聚，人以群分”，在自然科学和社会科学中，存在着大量的分类问题。 所谓类，通俗地说，就是指相似元素的集合。 而对于分类问题，我们通常不会提供 x 与 y 这样的映射关系，对于这种用机器自动找出 其中规律并进行分类的问题，我们称为聚类。 聚类在实际的应用中亦是非常广泛的，如：市场细分（Market segmentation）、社交 圈分析（social network analysis）、集群计算（organize computing clusters）、天体 数据分析（astronomical data analysis） 聚类与分类最大的区别在于，聚类过程为无监督过程，即待处理数据对象没有任何先验 知识，而分类过程为有监督过程，即存在有先验知识的训练数据集。 3.2 K-means 算法简介 K-Means 算法是典型的基于距离的聚类算法，其中 k 代表类簇个数，means 代表类簇内 数据对象的均值（这种均值是一种对类簇中心的描述），因此，K-Means 算法又称为 k-均值 算法。K-Means 算法是一种基于划分的聚类算法，以距离作为数据对象间相似性度量的标准， 即数据对象间的距离越小，则它们的相似性越高，则它们越有可能在同一个类簇。数据对象 间距离的计算有很多种，k-means 算法通常采用欧氏距离来计算数据对象间的距离。该算法
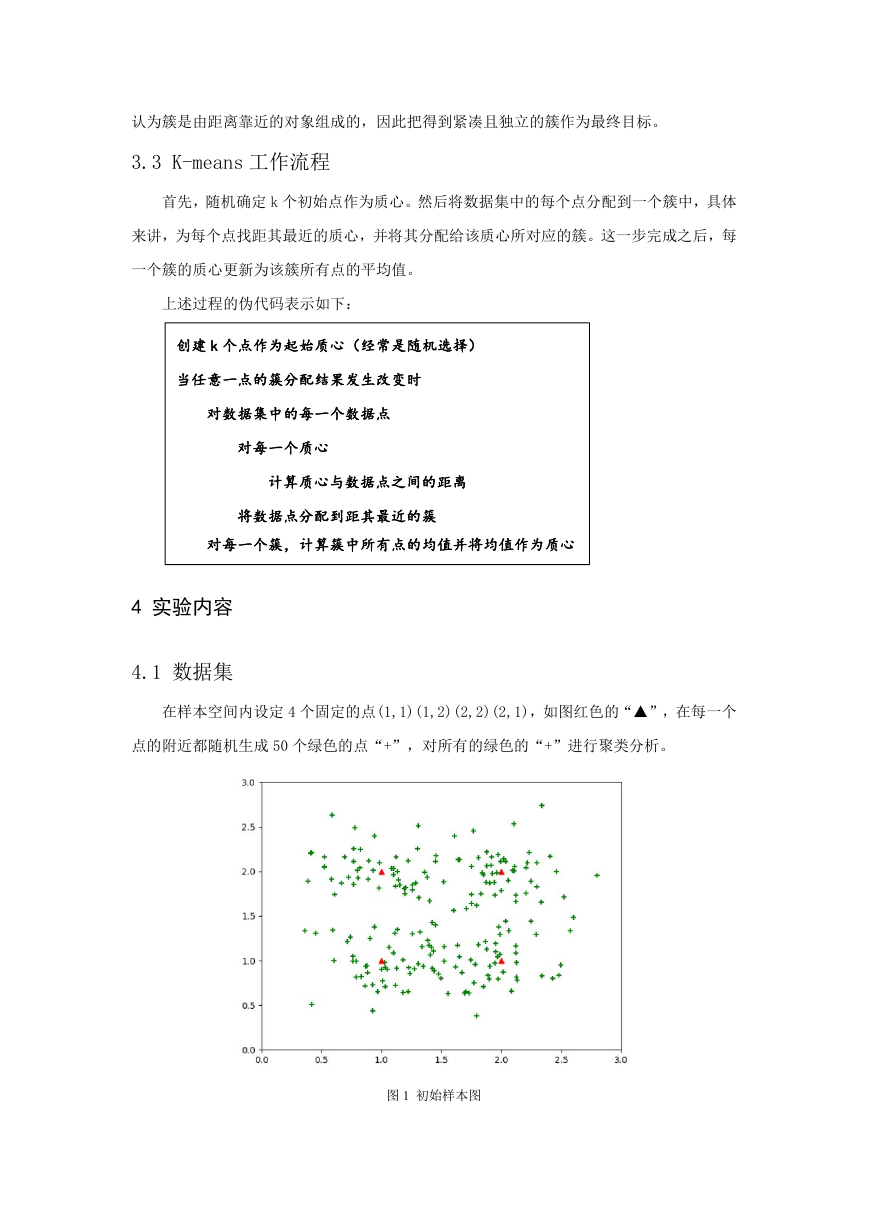
    认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。 3.3 K-means 工作流程 首先，随机确定 k 个初始点作为质心。然后将数据集中的每个点分配到一个簇中，具体 来讲，为每个点找距其最近的质心，并将其分配给该质心所对应的簇。这一步完成之后，每 一个簇的质心更新为该簇所有点的平均值。 上述过程的伪代码表示如下： 创建 k 个点作为起始质心（经常是随机选择） 当任意一点的簇分配结果发生改变时 对数据集中的每一个数据点 对每一个质心 计算质心与数据点之间的距离 将数据点分配到距其最近的簇 对每一个簇，计算簇中所有点的均值并将均值作为质心 4 实验内容 4.1 数据集 在样本空间内设定 4 个固定的点(1,1)(1,2)(2,2)(2,1)，如图红色的“▲”，在每一个 点的附近都随机生成 50 个绿色的点“+”，对所有的绿色的“+”进行聚类分析。 图 1 初始样本图
    4.2 实验步骤 （1）在四个中心点附近产生一堆数据 real_center = [(1, 1), (1, 2), (2, 2), (2, 1)] point_number = 50 points_x = [] points_y = [] for center in real_center: offset_x, offset_y = np.random.randn(point_number) * 0.3, np.random.randn(point_number) * 0.25 x_val, y_val = center[0] + offset_x, center[1] + offset_y points_x.append(x_val) points_y.append(y_val) points_x = np.concatenate(points_x) # 将二维数组拼接成一个 list points_y = np.concatenate(points_y) # 绘制点图 plt.scatter(points_x, points_y, color='green', marker='+') # 绘制中心点 center_x, center_y = zip(*real_center) plt.scatter(center_x, center_y, color='red', marker='^') plt.xlim(0, 3) plt.ylim(0, 3) plt.show() （2）随机选择 K 个点 K = 4 p_list = np.stack([points_x, points_y], axis=1) index = np.random.choice(len(p_list), size=K) centeroid = p_list[index] # 以下是画图部分 for p in centeroid:
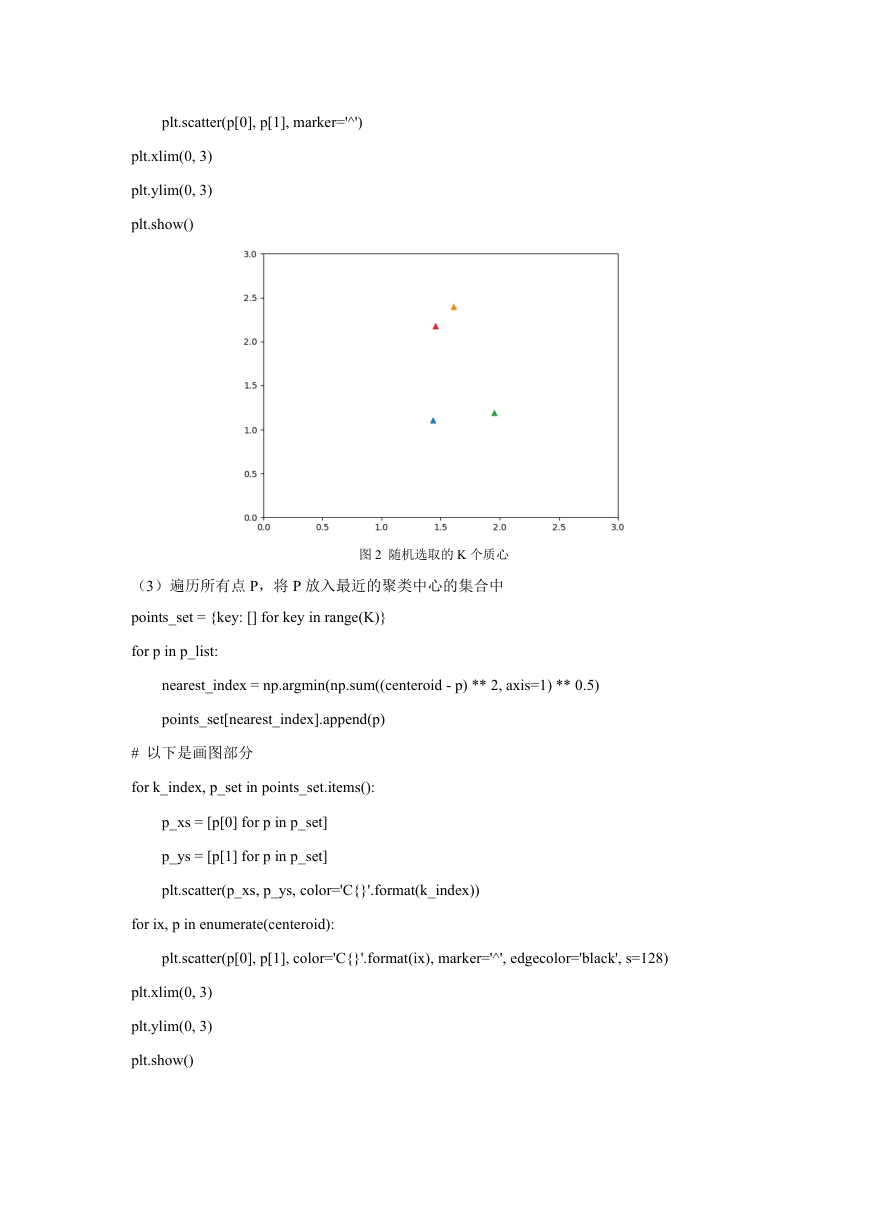
    plt.scatter(p[0], p[1], marker='^') plt.xlim(0, 3) plt.ylim(0, 3) plt.show() 图 2 随机选取的 K 个质心 （3）遍历所有点 P，将 P 放入最近的聚类中心的集合中 points_set = {key: [] for key in range(K)} for p in p_list: nearest_index = np.argmin(np.sum((centeroid - p) ** 2, axis=1) ** 0.5) points_set[nearest_index].append(p) # 以下是画图部分 for k_index, p_set in points_set.items(): p_xs = [p[0] for p in p_set] p_ys = [p[1] for p in p_set] plt.scatter(p_xs, p_ys, color='C{}'.format(k_index)) for ix, p in enumerate(centeroid): plt.scatter(p[0], p[1], color='C{}'.format(ix), marker='^', edgecolor='black', s=128) plt.xlim(0, 3) plt.ylim(0, 3) plt.show()
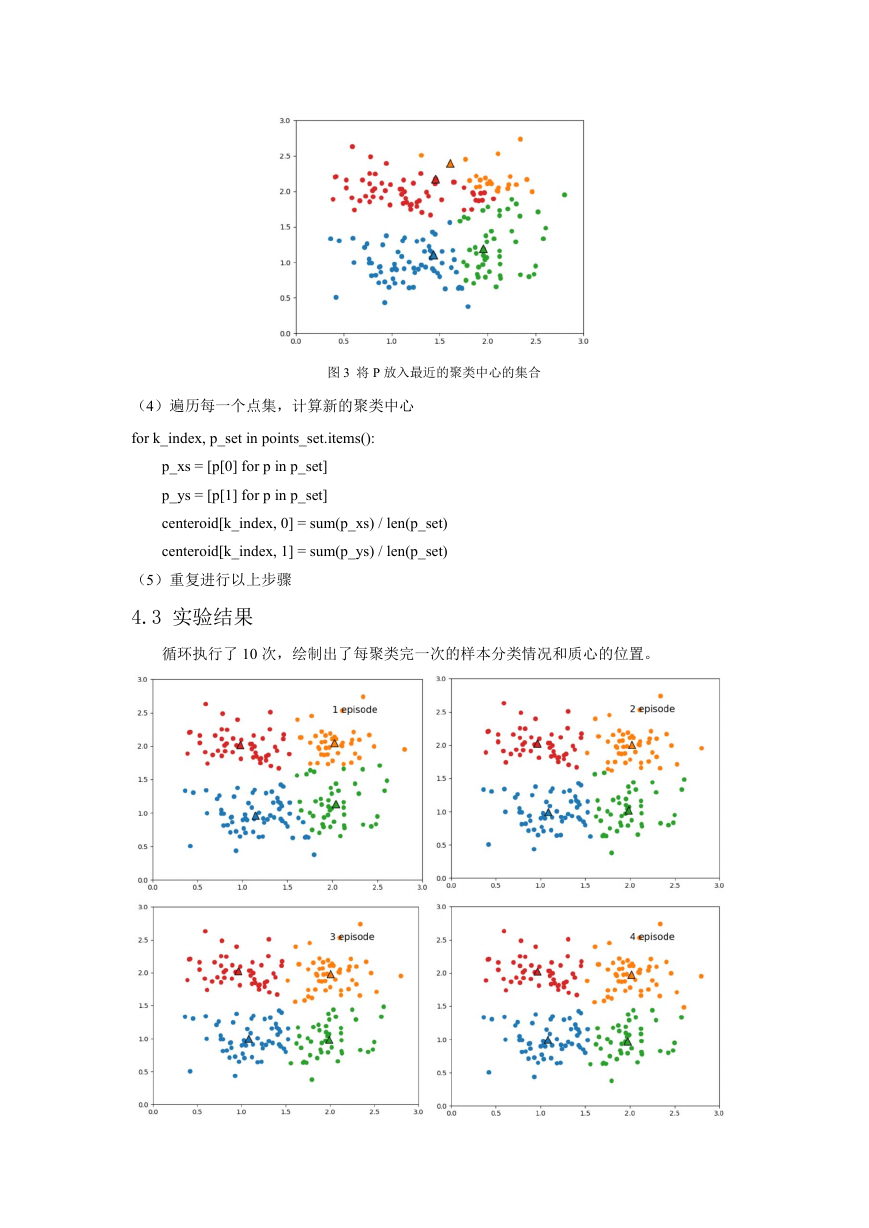
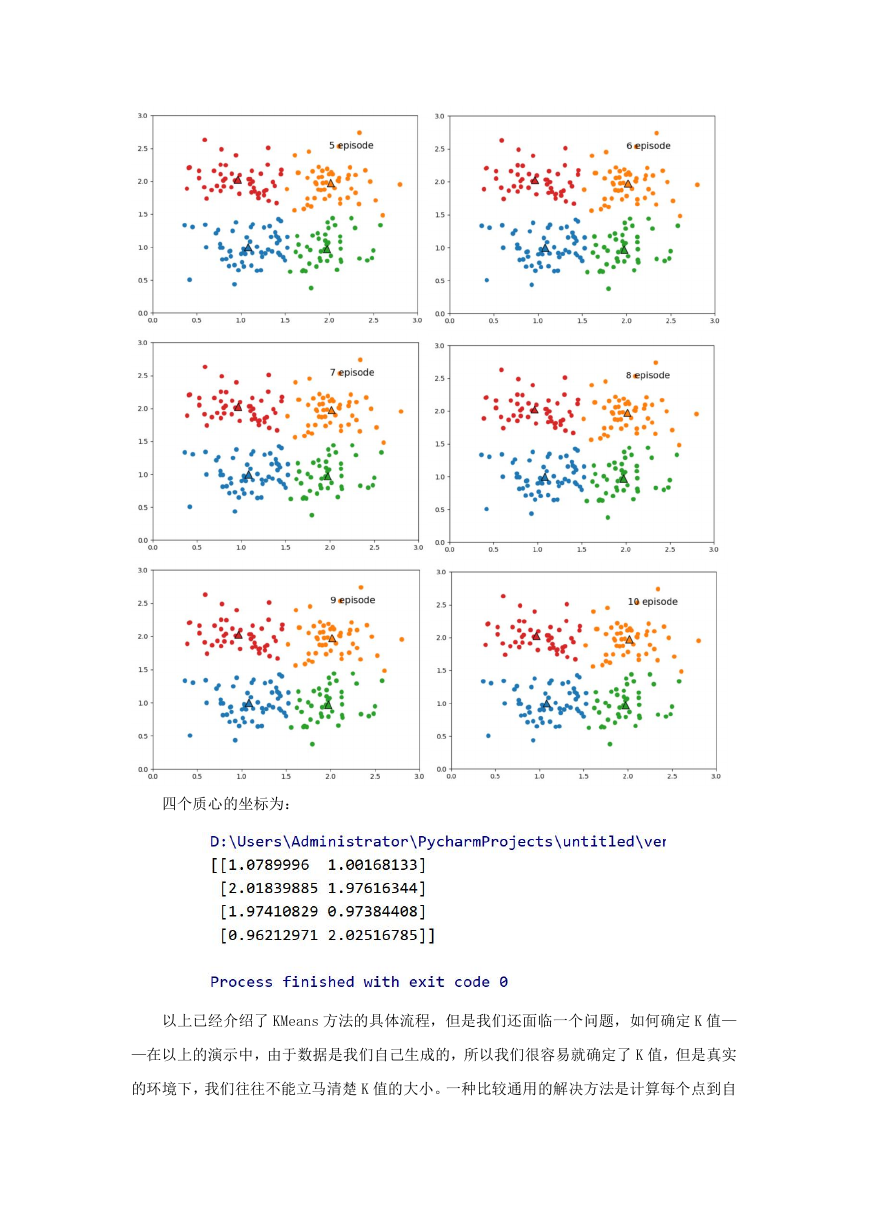
    图 3 将 P 放入最近的聚类中心的集合 （4）遍历每一个点集，计算新的聚类中心 for k_index, p_set in points_set.items(): p_xs = [p[0] for p in p_set] p_ys = [p[1] for p in p_set] centeroid[k_index, 0] = sum(p_xs) / len(p_set) centeroid[k_index, 1] = sum(p_ys) / len(p_set) （5）重复进行以上步骤 4.3 实验结果 循环执行了 10 次，绘制出了每聚类完一次的样本分类情况和质心的位置。
    四个质心的坐标为： 以上已经介绍了 KMeans 方法的具体流程，但是我们还面临一个问题，如何确定 K 值— —在以上的演示中，由于数据是我们自己生成的，所以我们很容易就确定了 K 值，但是真实 的环境下，我们往往不能立马清楚 K 值的大小。一种比较通用的解决方法是计算每个点到自
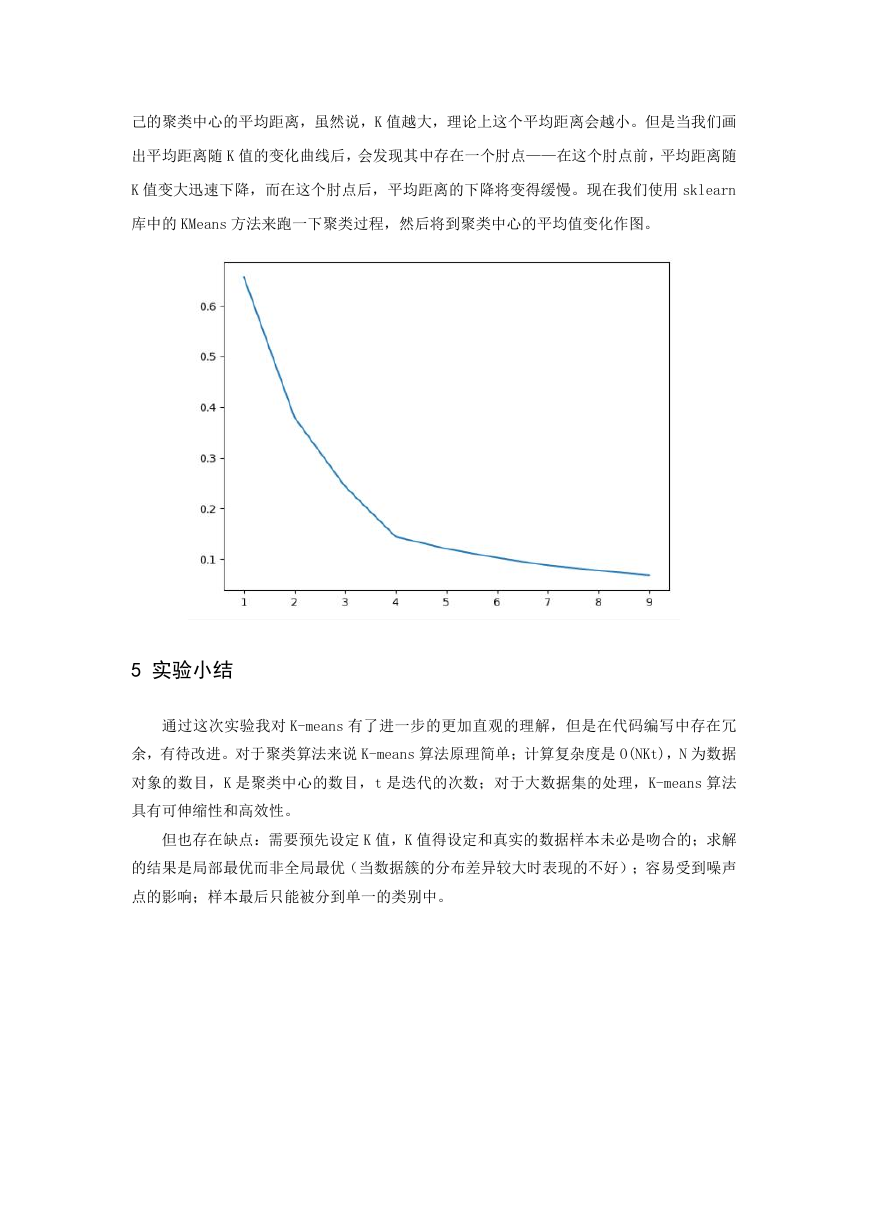
    己的聚类中心的平均距离，虽然说，K 值越大，理论上这个平均距离会越小。但是当我们画 出平均距离随 K 值的变化曲线后，会发现其中存在一个肘点——在这个肘点前，平均距离随 K 值变大迅速下降，而在这个肘点后，平均距离的下降将变得缓慢。现在我们使用 sklearn 库中的 KMeans 方法来跑一下聚类过程，然后将到聚类中心的平均值变化作图。 5 实验小结 通过这次实验我对 K-means 有了进一步的更加直观的理解，但是在代码编写中存在冗 余，有待改进。对于聚类算法来说 K-means 算法原理简单；计算复杂度是 O(NKt)，N 为数据 对象的数目，K 是聚类中心的数目，t 是迭代的次数；对于大数据集的处理，K-means 算法 具有可伸缩性和高效性。 但也存在缺点：需要预先设定 K 值，K 值得设定和真实的数据样本未必是吻合的；求解 的结果是局部最优而非全局最优（当数据簇的分布差异较大时表现的不好）；容易受到噪声 点的影响；样本最后只能被分到单一的类别中。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料