基于模糊路径纠偏的AGV视觉精定位研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.85M 资料格式：pdf 举报版权申诉

weixin_38691703-12934063-16359647455812752359.pdf-第1页.png

第1页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第2页.png

第2页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第3页.png

第3页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第4页.png

第4页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第5页.png

第5页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第6页.png

第6页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第7页.png

第7页 / 共10页

weixin_38691703-12934063-16359647455812752359.pdf-第8页.png

第8页 / 共10页

文本预览

基于模糊路径纠偏的AGV视觉精定位研究基于模糊路径纠偏的视觉精定位研究针对传统自主导航车(AGV)无法满足高精度路径跟踪和关键点精确定位问题，首次提出一种基于模糊控制的路径纠偏和二维码的关键点精确定位的组合方法。首先建立AGV四轮差动运动学模型，以位置偏差和角度偏差作为输入，纠偏控制量为输出设计一个二维模糊控制器实现快速纠偏。另外针对特殊点位高精度定位需求，根据每帧采样图片的尺寸固定这一特点建立基准坐标模型，通过三点定位法获取二维码轮廓，然后利用中心点的偏移计算误差，实现精确定位。 0 引言引言自动引导车(Automated Guided Vehicle，AGV)是现代物流行业的高效运输工具[1-3]。但是，在AGV运行过程中，导航定位精度差，一直制约其在许多工业环境下的应用。文献[4]提出一种最优偏差路径的AGV纠偏方法，可以实现5 mm范围内纠正，但是系统鲁棒性较差。文献[5]采用了一种基于惯性导航和视觉里程计的定位算法，实现视觉辅助定位，克服惯性导航的不足，但是仍然无法实现后期AGV的位置修正；文献[6]采用自定义定位标识符法，在地面铺设停车标识，系统识别停车标志符后，即根据直线运动公式计算AGV停车距离，直至距离为0，但后期缺少视觉信息反馈，不具备停车纠偏能力。针对以上情况，本文提出一种基于模糊控制和QR码的精确定位方法。首先通过模糊控制实现AGV快速路径纠偏，然后根据不同工位定位精度要求利用每帧图片尺寸不变特性实现QR码精确定位，实现了路径快速准确跟踪和特殊工位点精确定位。 1 AGV运动学模型运动学模型建立AGV四轮差动运动学模型，如图1所示[7-8]。坐标系XOY为AGV小车运行区域，视为大地坐标系，作为AGV运动坐标参考。X1O1Y1为以AGV小车几何中心建立的AGV车体坐标系，随AGV移动。AGV小车的位姿由小车几何中心在大地坐标系中的位置(X，Y)和AGV前进方向与大地坐标系的X轴正方向的夹角θ确定，即P=[X，Y，θ]T。图1中，o1、o2分别为AGV小车前后驱动单元的中心；L为驱动单元中心距AGV小车几何中心的距离；B为各驱动轮中心到各自驱动单元中心的距离；α1、α2分别为两个驱动单元中轴线与AGV小车坐标系X1轴正方向的夹角，按照顺正逆负取值； Vo1、Vo2分别为两个驱动单元中心点的线速度；A点为AGV小车的瞬时转动中心。同时，假设： (1)两个驱动单元中心的角速度分别为ωo1、ωo2； (2)4个轮毂电机的线速度和角速度分别为v1、v2、v3、v4、ω1、ω2、ω3、ω4； (3)前后两个驱动单元的中点在大地坐标系中的坐标点分别设为(Xo1、Yo1)、(Xo2、Yo2)。根据P=[X，Y，θ]T即AGV几何中心的位置，可以得到两个驱动单元中心点的大地坐标为：

通过以上运动模型可知，只要控制前后两个驱动单元的运动速度和加速度，就可以控制AGV小车的运行状态。 AGV小车模型如图2所示，主要由工控机+显示屏模块、视觉模块、驱动模块构成。

2 模糊纠偏设计模糊纠偏设计 2.1 模糊控制原理模糊控制原理模糊控制是一种相比于传统控制更加贴近于人类思维的控制方法。与传统的控制方式不同之处是，模糊控制技术在复杂的多变量系统中可以通过各种变量之间的关系完成对系统进行控制，从而使得系统的控制在直观上更加简便[9-10]。模糊控制基本原理如图3所示。 2.2 模糊控制器设计模糊控制器设计模糊控制规则输出曲面如图4所示，可以看出模糊控制规则曲面在E或EC在零值附近时波动比较大，利于精确控制；在E或 EC绝对值较大时曲面波动小，系统具有较强的鲁棒性。

模糊量清晰化处理即为把模糊推理得出的结果转换为控制系统可以识别的确定值。通过重心法计算横坐标轴和隶属度函数曲线围成的区域重心，如式(7)所示。 3 QR码关键点精确定位码关键点精确定位 3.1 二维码二维码3点定位点定位根据二维码的3个位置探测图形形状相同位置对称，所以采用3点定位法确定二维码位置。首先确定3个位置探测图形中点坐标，然后通过直线拟合法获取关键4点坐标，最终确定整个二维码区域。定位结果如图5所示。 3.2 QR码精定位原理码精定位原理视觉定位相机安装在AGV底板中心下面，距离地面高度为25 cm。

AGV的位移纠偏移动方向如图7所示，根据S1、S2值的正负可以实现AGV的4个方向自由纠偏运动，从而避免对另外两个边距的冗余计算。

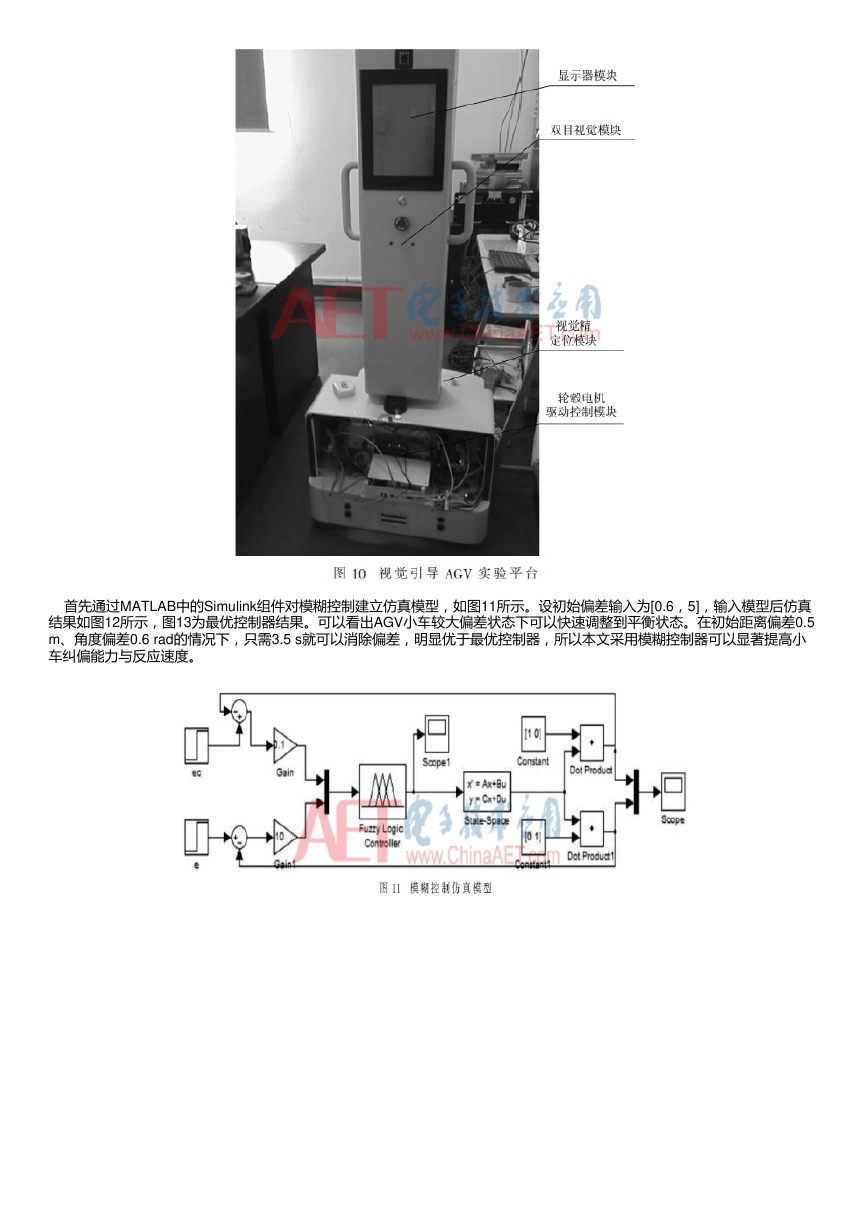
最后通过反余弦变换求得偏转角α，旋转纠偏方向如图9所示。取水平方向为0°方向，当偏差角度为正则顺时针旋转AGV纠偏，反之逆时针旋转AGV。 4 实验验证实验验证实验采用自主研发的基于激光雷达+视觉引导的AGV实验平台，如图10所示。实验环境为工厂的地坪漆地面，采用黑白二维码作为标识符，单目相机采样分辨率为1 280×720。

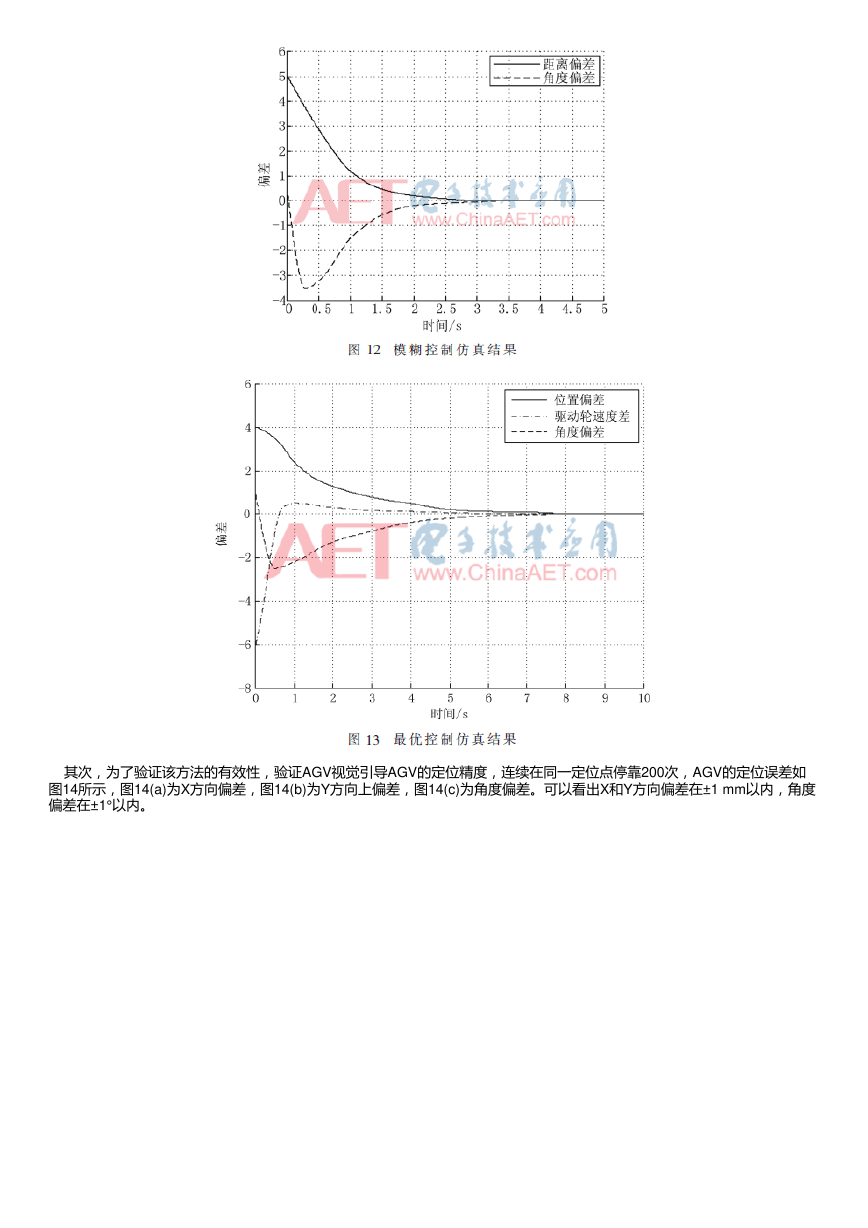
首先通过MATLAB中的Simulink组件对模糊控制建立仿真模型，如图11所示。设初始偏差输入为[0.6，5]，输入模型后仿真结果如图12所示，图13为最优控制器结果。可以看出AGV小车较大偏差状态下可以快速调整到平衡状态。在初始距离偏差0.5 m、角度偏差0.6 rad的情况下，只需3.5 s就可以消除偏差，明显优于最优控制器，所以本文采用模糊控制器可以显著提高小车纠偏能力与反应速度。

其次，为了验证该方法的有效性，验证AGV视觉引导AGV的定位精度，连续在同一定位点停靠200次，AGV的定位误差如图14所示，图14(a)为X方向偏差，图14(b)为Y方向上偏差，图14(c)为角度偏差。可以看出X和Y方向偏差在±1 mm以内，角度偏差在±1°以内。

分享到：

赞收藏

资料库

基于模糊路径纠偏的AGV视觉精定位研究.pdf

相关推荐

开发技术

热门标签

最新资料