基于分形导数、分数阶导数的新型生物热传递方程.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 基于分形导数、分数阶导数的新型生物热传递方程孙逸飞, 陈文河海大学工程力学系，南京（210098） E-mail: sunny@hhu.edu.cn 摘要：本文基于热力学第一定律与经典 Pennes 生物热传递方程的基本理论，结合非傅里叶热传导的相关概念，首次提出了两种新的生物组织热传递方程：分形导数、分数阶导数生物热传递方程。并选取皮肤组织的分数阶热传递模型与经典 Pennes 等模型做了数值比较，结果显示：分数阶导数生物热传递模型是合理的，适当选取阶数α值，可以得到与其他模型极为相近的预测结果；分数阶模型的预测值小于经典 Pennes 模型预测值，但α越接近与 2 时，其预测结果越接近于经典 Pennes 模型；皮肤组织分数阶热传递方程的阶数α的大致取值范围在 1.85-2.0 之间。关键词：生物热传递；非傅里叶热传导；分形导数；分数阶导数；分形梯度律中图分类号：Q65；O551 0 引言近年来生物医学工程领域内诸如肿瘤热疗、低温外科等临床医学的发展，要求人们更为精确的构建生物软组织温度场。然而，温度场重构的效果很大程度上依赖于其所选热传递方程，所以建立一个相对精确的生物热传递方程是相当有必要的。经典 Pennes 生物热传递方程[1]是基于傅里叶热传导定律推出的，由于其方程简单，物理概念清晰，因而得到了广泛的应用。但是实际情况下，生物组织中的热流存在弛豫现象，其热传递过程并不遵循经典傅里叶梯度率。为了考虑这一非傅里叶热传递效应，许多学者[2,3] 提出了多种微分方程模型。目前应用较广泛的是包含有热弛豫时间的整数阶微分生物热传递方程。然而，非傅里叶热传递过程本质上是时间记忆性、空间非局域性的过程[4]，整数阶导数极限定义具有局域性，因此整数阶微分热传递方程不能准确地描述这类非傅里叶热传递过程。分数阶导数被证明能够较精确地描述有记忆和遗传、路径依赖性质的物理过程[5]，因而其相关理论被广泛应用于生物、土木以及电气等工程领域[6,7]。除分数阶导数外，分形导数可由尺度变换[8]得到，适用于描述复杂多孔介质（如生物软组织）中的反常物理行为。本文利用分形导数、分数阶导数的这些优势，联系热力学第一定律与 Pennes[1]生物热传递方程的基本理论，首次提出了分形导数、分数阶导数生物热传递方程。本文分为五大节，结构如下：第一节介绍了分形导数、分数阶导数的物理背景和数学基础；第二节介绍了经典 Pennes 生物热传递方程的基本理论；第三节推导分形导数、分数阶导数生物热传递方程；第四节通过数值分析，比较了新模型与经典 Pennes 模型以及文献[13] 的计算结果；最后一节总结全文。 1 分形导数、分数阶导数 1.1 分形导数分形是广泛存在于物质空间结构和物理过程时间演化中的自相似现象。在分形尺度中，尺度由整数维时空(x, t)转变为分形时空（xα, tβ），文献[8]基于尺度转换定义了分形尺度下的导数，即分形导数 - 1 -

中国科技论文在线 http://www.paper.edu.cn du x ( ) dx α = lim x x ' → u x ( ) x α − − u x ( ') x ' α 。 (1) 文中还提出了分形尺度下的两个假设：1、在任意分形尺度下，物理定律的形式保持不变；2、在“反常”物理过程中，“反常”环境对物理过程的影响等价于分形尺度转换所产生的影响。基于这两个假设，我们可以利用分形导数描述分形尺度下的物理过程。 1.2 分数阶导数分数阶微积分并不是一个新的数学理论。早在 300 多年前，Leibnitz 和 L’ Hospital 在两人的通信中首先提出了分数阶导数的概念。但由于那时分数阶微积分的物理背景不是很清楚，因此一直发展缓慢。直至近几十年，人们发现分数阶导数模型能够较好地描述“反常” 行为，分数阶微积分的研究和应用才有了充分的发展。目前，分数阶微积分的数学理论已较为完善，并有了广泛的应用[5,6,7]。时间分数阶导数三种主要的定义，Gruwald-Letnikov 定义、 Riemann-Liouville 定义及 Caputo 定义，这三种定义在一定条件下可统一[5]。下面仅介绍文中用到的 Gruwald-Letnikov 分数阶导数[5]（p 为导数的阶数）： p d f x ( ) p dx = ⎛ 其中 a 为初始位置， ⎜ ⎝ p r ⎞ ⎟ ⎠ = lim h 0 → x a nh − = p p ( h − p n ∑ r = 0 ( 1) − − 1)( p − 2 r f x ( ⎞ ⎟ ⎠ p r ( r p r ⎛ ⎜ ⎝ ) ! − rh ) ， (2) − + 1) 。Gruwald-Letnikov 分数阶导数由整数阶导数的差分形式扩展得到，通常作为分数阶导数的差分近似用于分数阶导数方程的数值求解。 2 经典 Pennes 生物热传递方程及其相关理论 Pennes[1]在推导生物热传递方程时，提出了一些假设，他认为生物体内热量的改变主要由下列因素引起： 1. 组织内温度梯度引起的热传导导致的能量传递。 2. 组织内血液流动引起的热对流导致的能量传递。 3. 组织内新陈代谢以及热辐射引起的能量传递。 4. 由外界环境引起的组织内能量传递。基于以上假设，忽略第三项的“新陈代谢以及热辐射”因素，Pennes 定义生物热传递方程如下： + ρ c w T x t ( , ) b b [ b b − T x t ( , )] + S x t ( , ) ， (3) k ∂ = c ρ T x t ( , ) ∂ t ∂ T x t ( , ) 2 x 2 ∂ ) kg m ， bc 为血液比热 ( ( T x t 为组织温度 ( ) 3 ) J kg C° ， bρ 为 T x t 为血液温其中 k 为热传导系数 ( W m C° ，ρ为组织密度 ( kg m ，c 为组织比热 ( ) 3 血液密度度 ( )C° ， ( , ) 这里，综合热力学第一定律与 Pennes 热传递方程的基本理论，我们可以用下式定义生 )C° ， ( , ) 3 ) m s m ， b ( , ) J kg C° ， bw 为血液灌注率 3 ( W m 。 S x t 为外界环境作用的热量 ( ) ) 3 物组织内热量守恒公式： Q + Q + S ， (4) 其中 TQ 为生物组织热量的变化， DQ 为组织内热传导引起的热量变化， CQ 为组织内热对 =T Q D C E - 2 -

中国科技论文在线 http://www.paper.edu.cn 流引起的热量变化， ES 为外界环境作用引起的热量变化。 3 分形导数、分数阶导数生物热传递方程 3.1 分形导数生物热传递方程传统傅里叶理论[9]认为：经介质传导的热量 Q 与热传导方向相垂直的横截面 A，经过介 T− 和传导时间 t∆ 成正比，与传导距离 L∆ 成反比。引入比例常数 k，即热传 ) T ( 质后的温差 2 导率，Fourier 定律可以写为： 1 Q = − kA T ( 2 − T 1 ) ∆ ∆ ， (5) t L 负号为热力学第二定律规定，热量自发地由高温区向低温传递。引入热流量 q，定义为： k T ( − 2 L∆ → 时，上式就是经典傅里叶梯度律： q Q A t ∆ = − T 1 = 0 ( ) ) 当 q = − ∇ 。 (7) 现在将生物组织看作多孔介质，则基于文献[8]的理论，我们可以假设，生物组织某一 k T ∆ ， (6) L 区域的热量 Q 可能不是反比于 L∆ ，而是反比于分形空间转换尺度 Lα∆ ，即： = − Q − ) kA T ( 2 T 1 指数α为待定系数，与介质本身物理性质有关。同样的，当： ∆ ∆ ， (8) t Lα Lα∆ → 时，可以得到下 0 列分形非傅里叶梯度律： q = − k T x t ( , ) ∂ xα ∂ 。 (9) 基于这一新型分形非傅里叶梯度律，我们可以定义下列表达式：生物组织热量总的变化 T x t ( , ) ∂ t ∂ 其中 ρ为组织密度， c 为组织比热， ( , ) c ρ TQ = ， (10) T x t 为组织温度；生物组织内热传导引起的热量变化 DQ = k ∂ ∂⎡ ⎢ x ∂ ∂⎣ T x t ( , ) xα ⎤ ⎥ ⎦ ， (11) 其中 k 为热传导系数，α为待定系数， ( , ) T x t 为组织温度；生物组织内热对流引起的热量变化 CQ ρ= c w T x t ( , ) b b b( b − T x t ( , )) ， (12) T x t 为 T x t 为血液温度， ( , ) 其中 bρ 为血液密度， bc 为血液比热， bw 为血液灌注率， b ( , ) 组织温度；外界环境作用引起的热量变化 S x t 。 (13) ( , ) 将以上表达式(10)~(13)代入热量守恒方程(4)，得到分形生物热传递方程： c ρ T x t ( , ) ∂ t ∂ = k ∂ ∂⎡ ⎢ x ∂⎣ ∂ T x t ( , ) xα ⎤ ⎥ ⎦ + ρ c w T x t ( , ) b b [ b b − T x t ( , )] + S x t ( , ) 。 (14) 显然，当α取 1 时，分形导数热传递模型退化为经典 Pennes 模型。 - 3 -

中国科技论文在线 http://www.paper.edu.cn 4.2 分数阶导数生物热传递方程 Feller[10]在研究反常扩散运动时，提出了一个空间分数阶导数的扩散控制方程： u x t ( , ) ∂ t ∂ = C u x t ( , ) ,1 α ∂ x α ∂ < α < 2 ， (15) 其中u 为点 ( , )x t 处的浓度，C 为常数。文献[11,12]进一步研究指出：“扩散”是一个广义概念，包含各种传输过程，当u 被定义为温度时，方程(15)就变成非傅里叶热传导的控制方程。根据这一理论，我们可以定义由生物组织内热传导引起的热量变化量的表达式： DQ = k T x t ( , ) α ∂ x α ∂ ， (16) 其中 bρ 为血液密度， bc 为血液比热， bw 为血液灌注率， b ( , ) T x t 为组织温度，α为待定系数。至此，联系表达式(10)、(12)、(13)、(16)，代入热量守恒方程(4)，得分数阶导数生物热传递方程： T x t ( , ) α ∂ x α ∂ T x t 为血液温度， ( , ) T x t ( , ) ∂ t ∂ 2α< < 。 (17) T x t ( , )] S x t ( , ) ρ c w T x t ( , ) b b [ b b = k c ρ + − + ，1 显然，当α取 2 时，分数阶导数模型退化为经典 Pennes 热传递模型。 4 数值分析 4.1 计算模型与计算方法本节选取人体皮肤组织热传递作为讨论对象，使用分数阶导数模型建模，通过选取适当的α值，与相应的 Pennes 皮肤热传递方程，以及文献[13]中考虑热弛豫时间的微分型热传递方程进行比较，分析模型。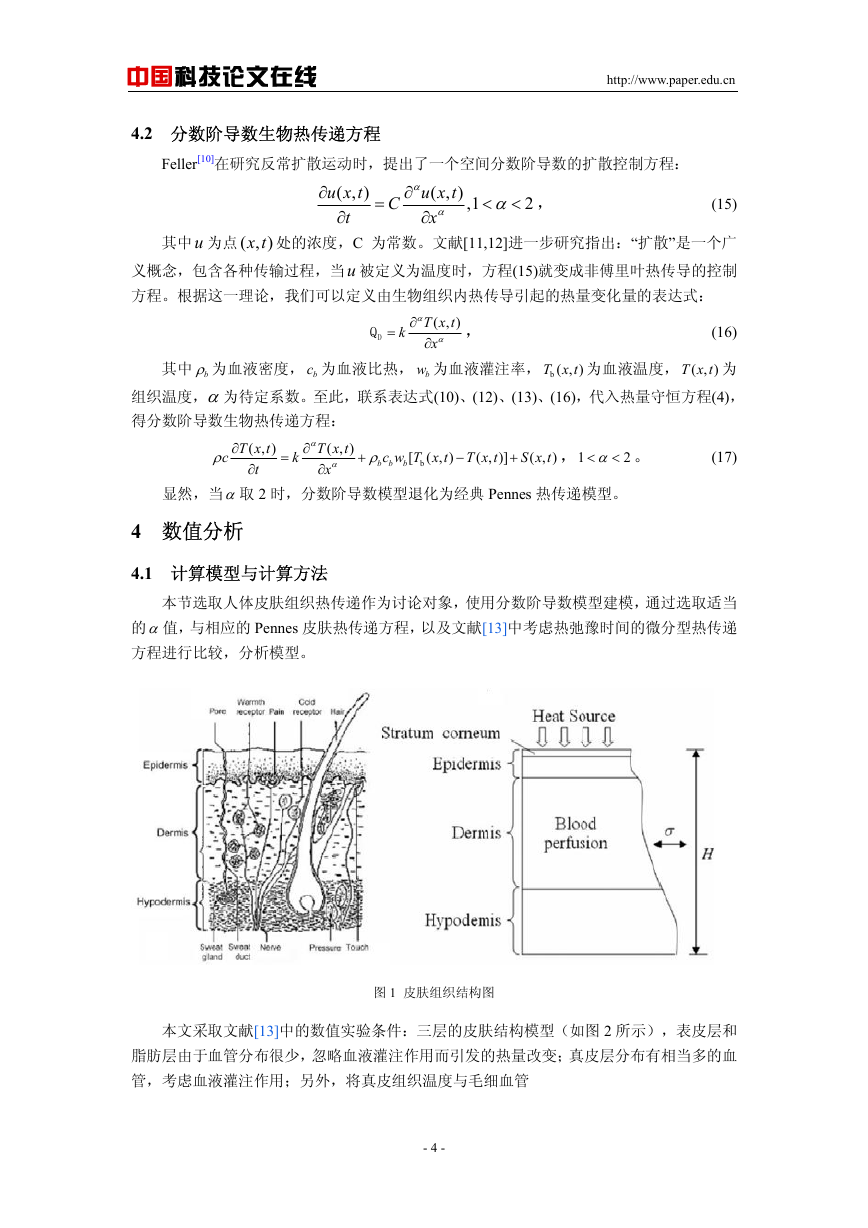图 1 皮肤组织结构图本文采取文献[13]中的数值实验条件：三层的皮肤结构模型（如图 2 所示），表皮层和脂肪层由于血管分布很少，忽略血液灌注作用而引发的热量改变；真皮层分布有相当多的血管，考虑血液灌注作用；另外，将真皮组织温度与毛细血管 - 4 -

中国科技论文在线 http://www.paper.edu.cn 表 1 皮肤热传递模型的相关参数表皮层真皮层脂肪层 (mm) 厚度 3 6 ) × 热导率 J m K ) ml Blood ml ( 10 × 密度比热容 J mK ( tissue s / / ) W m ( 3 新陈代谢产热率 ( ) 血液灌注率 0.1 3.182 0.21 0 368.1 1.5 2.846 0.37 0~0.1 368.1 4.4 1.975 0.16 0 368.3 内血液温度视为一致，静脉血管等粗血管血液温度 b ( , ) T x t 视为恒定。相关皮肤组织参数列于表（1）。边界条件与初始条件如下：初始条件 T x ( ,0) = 37 C° ，边界条件 1. 皮肤左右边界处 T x t ( , ) ∂ t ∂ t = 0 = 0 ； (18) T t (0, ) T= ， ( T e ∞ = 。 (19) t , ) T b 2. 皮肤层交界处其中 1 t T l ( , ) 1 1 ( , ) = T x t T x t T x t 分别为各层皮肤的温度； T x t ( , ) ∂ 2 x ∂ 2 T x t ( , ) ∂ 1 x ∂ T x t ( , ) ∂ 2 x ∂ ， 2 T l ( ( , ), ( , ), T l ( 2 = − ， t , ) t , ) − k − k 1 k 2 = 2 2 3 x x = 1 2 x x = 1 = − k 3 T x t ( , ) ∂ 3 x ∂ x x = 2 x x = 2 。 (21) T l t ( , ) 3 3 ， (20) 4.2 数值计算与结果分析本文采用有限差分方法，对于分数阶模型我们选取不同的α值用 Matlab 编程求解，差分方法的具体细节置于附录中，不在此详述。与经典 Pennes 方程的数值比较结果用图表显示如下： - 5 -

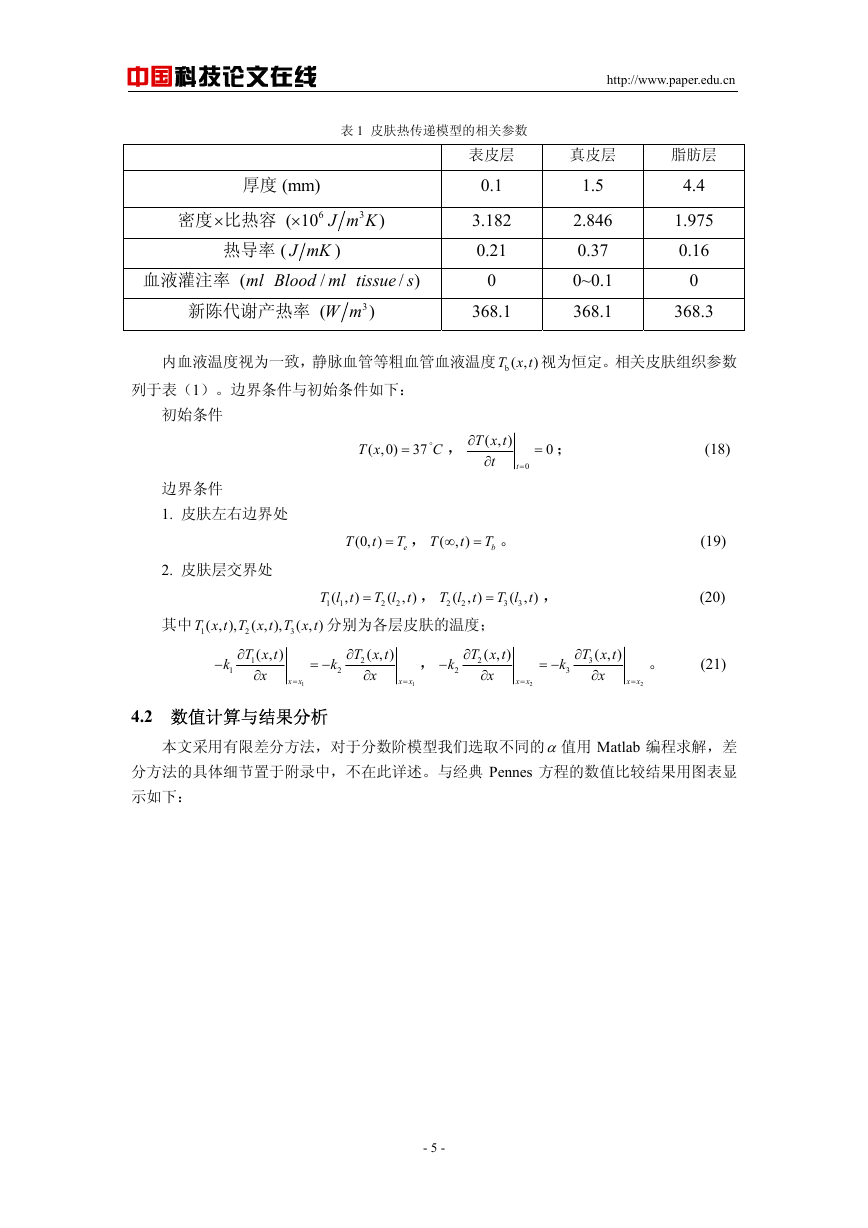
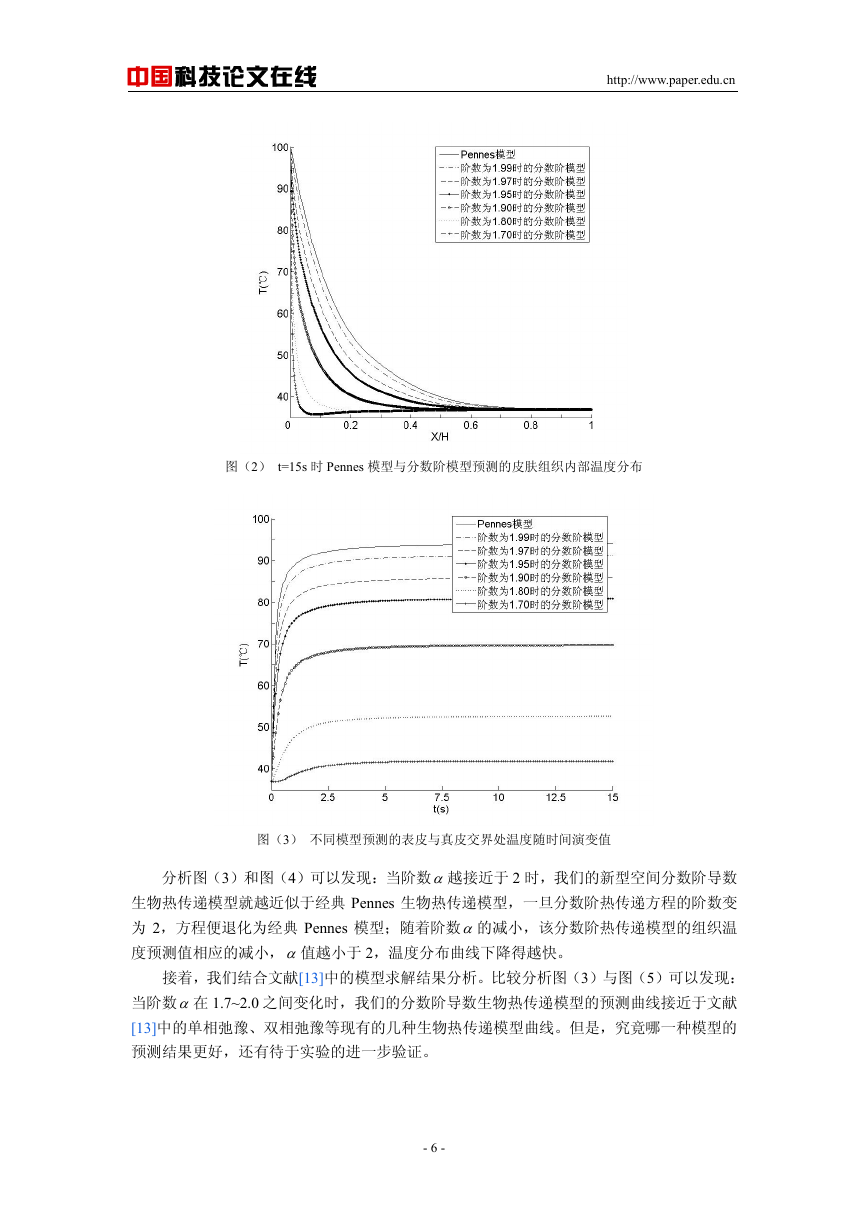
中国科技论文在线 http://www.paper.edu.cn 图（2） t=15s 时 Pennes 模型与分数阶模型预测的皮肤组织内部温度分布图（3）不同模型预测的表皮与真皮交界处温度随时间演变值分析图（3）和图（4）可以发现：当阶数α越接近于 2 时，我们的新型空间分数阶导数生物热传递模型就越近似于经典 Pennes 生物热传递模型，一旦分数阶热传递方程的阶数变为 2，方程便退化为经典 Pennes 模型；随着阶数α的减小，该分数阶热传递模型的组织温度预测值相应的减小，α值越小于 2，温度分布曲线下降得越快。接着，我们结合文献[13]中的模型求解结果分析。比较分析图（3）与图（5）可以发现：当阶数α在 1.7~2.0 之间变化时，我们的分数阶导数生物热传递模型的预测曲线接近于文献 [13]中的单相弛豫、双相弛豫等现有的几种生物热传递模型曲线。但是，究竟哪一种模型的预测结果更好，还有待于实验的进一步验证。 - 6 -

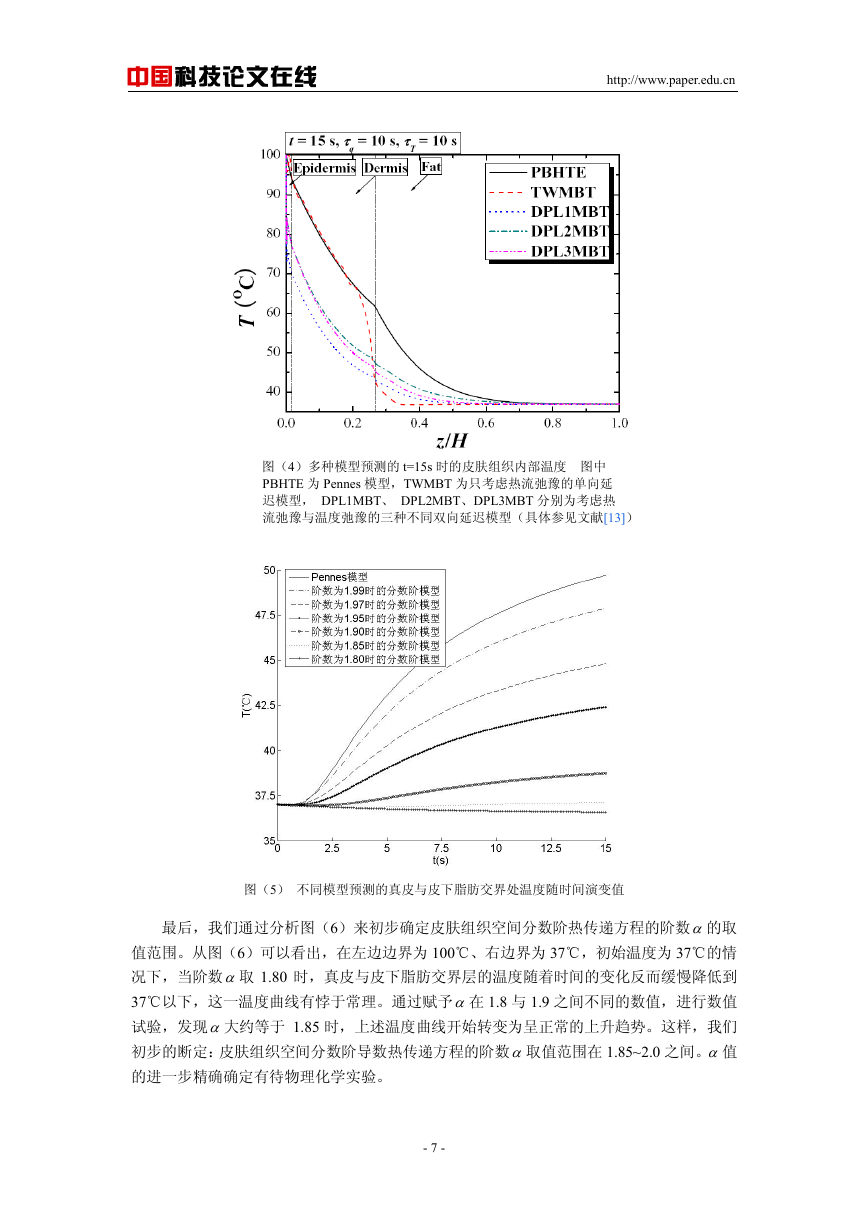
中国科技论文在线 http://www.paper.edu.cn 图（4）多种模型预测的 t=15s 时的皮肤组织内部温度图中 PBHTE 为 Pennes 模型，TWMBT 为只考虑热流弛豫的单向延迟模型， DPL1MBT、 DPL2MBT、DPL3MBT 分别为考虑热流弛豫与温度弛豫的三种不同双向延迟模型（具体参见文献[13]）图（5）不同模型预测的真皮与皮下脂肪交界处温度随时间演变值最后，我们通过分析图（6）来初步确定皮肤组织空间分数阶热传递方程的阶数α的取值范围。从图（6）可以看出，在左边边界为 100℃、右边界为 37℃，初始温度为 37℃的情况下，当阶数α取 1.80 时，真皮与皮下脂肪交界层的温度随着时间的变化反而缓慢降低到 37℃以下，这一温度曲线有悖于常理。通过赋予α在 1.8 与 1.9 之间不同的数值，进行数值试验，发现α大约等于 1.85 时，上述温度曲线开始转变为呈正常的上升趋势。这样，我们初步的断定：皮肤组织空间分数阶导数热传递方程的阶数α取值范围在 1.85~2.0 之间。α值的进一步精确确定有待物理化学实验。 - 7 -

中国科技论文在线 http://www.paper.edu.cn 5 结论本文首次提出了分形导数、分数阶导数生物热传递方程，选取了其中的分数阶导数热传递方程与经典 Pennes 等生物热传递方程进行比较分析，我们得出以下结论：新型分数阶导数生物热传递方程式合理的。适当选取α值，分数阶模型可以得到与其他模型极为相近的预测结果。当阶数α越接近于 2 时，分数阶导数生物热传递模型就越近似于经典 Pennes 生物热传递模型，一旦分数阶热传递方程的阶数变为 2，方程便退化为经典 Pennes 模型。随着阶数α的减小，该分数阶热传递模型的组织温度预测值相应的减小，α值越小于 2，温度分布曲线下降得越快。皮肤组织的阶数α之于 1.85~2.0。由于生物组织分形结构的复杂性，本文认为此空间分形导数热传递方程与空间分数阶导数热传递方程可能更适用于生物组织热传递过程的模拟。当然，利用分形导数、分数阶导数建立的生物热传递模型都是唯象模型，由于生物传热机理较为复杂，因此，我们的模型是否确实能够更好的解释这一过程的，这还有待于进一步的研究。附录：本文采用有限差分法 [5,14] ，取时间步长 t∆ 、空间步长 x∆ ，以中心点 ( x t , i j + 1 2 ) 取 Crank-Nicholson 六点差分格式来表示 Pennes 皮肤热传递方程： c ρ j T i j T i 1 + − t ∆ = k T i j 1 + 1 + − T 2 i j 1 + + T j 1 + + i 1 − x 2 2 ∆ T i j 1 + − T 2 i j + T i j 1 − + c w T [ ρ b b b b − j T i j T i 1 + + 2 ] + S ， (22) 联合边界条件，整理得隐式差分公式 ⎤ ⎡ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ j + 1 T 1 j + 1 T 2 T n j 1 + 1 − j + 1 T n ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ N 2 ， (23) 2 h xM ∆ k M + − N 2 M − − 2 M 1 2 + M + N 2 − M − M 1 2 + M + N 2 − M − 2 M 1 2 + M + ⎡ 1 2 + ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ (1 2 − M − N 2 MT 1 2 + j + h xM ∆ k − (1 2 M j T ) 1 − 2 j MT 2 − 4 h xM ∆ k T e j T MT ) 2 3 + j + N 2 MT n j − 2 + (1 2 − M − 2 MT n j 1 − + (1 2 − N 2 M T j ) n 1 − N 2 − + j MT n j T ) n - 8 - ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ + Q 1 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ 1 ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ 1 ⎢ ⎥ ⎢ ⎥ 1 ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ 1 ⎣ ⎦

资料库

基于分形导数、分数阶导数的新型生物热传递方程.pdf

相关推荐

开发技术

热门标签

最新资料