2015年云南昆明理工大学材料力学考研真题A卷.doc

发布时间：2022-09-16 发布人：admin 分类：说明书资料大小：0.35M 资料格式：doc 举报版权申诉

第1页 / 共4页

第2页 / 共4页

第3页 / 共4页

第4页 / 共4页

文本预览

2015 年云南昆明理工大学材料力学考研真题 A 卷一、概念题（包含单选选择题和填空题，每小题 4 分，15 小题，共 60 分） 1. 在下列关于内力与应力的讨论中，正确的说法是。 A．内力是应力的代数和； C．应力是内力的平均值； B．内力是应力的矢量和； D．应力是内力的分布集度。 2. 冷作硬化现象是指材料。 A．由于温度降低，其弹性极限提高，塑性降低； B．由于温度降低，其弹性模量提高，泊松比减小； C．经过塑性变形，其弹性极限提高，塑性降低； D．经过塑性变形，其弹性模量提高，泊松比减小。 3. 等截面直杆承受拉力 F作用，若选用三种不同的截面形状：圆形、正方形、空心圆。比较材料用量，则。 A．正方形截面最省料； C．空心圆截面最省料； B．圆形截面最省料； D．三者用料相同。 4. 根据圆轴扭转的平面假设．可以认为圆轴扭转时其横截面。 A．形状尺寸不变，直径仍为直线； C．形状尺寸不变，直径不保持直线； B．形状尺寸改变，直径仍为直线； D．形状尺寸改变，直径不保持直线。 5. T 形截面梁，两端受力偶矩 M0 作用，如图示。若材料的抗压许用应力[σc]大于抗拉许用应力[σt]，则梁截面的位置应如何安放才合理？答：。 M0 M0 A B C D 6. 在下列关于平面图形的结论中，是错误的。 A．图形的对称轴必定通过形心； B．图形两个对称轴的交点必为形心； C．图形对对称轴的静矩为零； D．使静矩为零的轴为对称轴。 7. 图示结构受力如图所示。构件 A和 B的直径都为 d，则两者中最大剪应力为。 A．4bF /(aπd2) ； B．4(a+b) F / (aπd2)； C．4(a+b) F /(bπd2)； D．4a F /(bπd2) 。 B A 8. 梁的挠度是指。 a b

A．横截面上任一点沿梁轴垂直方向的线位移； B．横截面形心沿梁轴垂直方向的线位移； C．横截面形心沿梁轴方向的线位移； D．横截面形心的位移。 9. 在用能量法推导冲击动荷系数 Kd 时，有人作了以下假设，其中是不必要。 A．冲击物的变形很小，可将其视为刚体； B．被冲击物的质量可以忽略、变形是线弹性的； C．冲击过程中只有变形能、位能和动能的转化，无其它能量损失； D．被冲击物只能是杆件。 10. 在下列说法中，是正确的。 A．在有正应力作用的方向，必有线应变； B．在无正应力作用的方向，必无线应变； C．在线应变为零的方向，正应力也—定为零。 11．设一梁在广义力 P1、P2 共同作用下的外力功为 W  1  112 P 2  P  2  。若 P1 为集中力、 P2 为集中力偶，则δ1、δ2 A．分别为线位移和角位移； C．均为线位移；。 B．分别为角位移和线位移； D．均为角位移。 12. 构件在交变应力作用下发生疲劳破坏，以下结论中是错误的。 A. 断裂时的最大应力小于材料的静强度极限； B. 用塑性材料制成的构件，断裂时有明显的塑性变形； C. 用脆性材料制成的构件，破坏时呈脆性断裂； D. 断口表面一般可明显地分为光滑区和粗粒状区。 13. 杆件在变形时，其危险点的应力状态为如下单元体所示状态。 A. 斜弯曲； B. 偏心拉伸； C. 拉弯组合； D. 弯扭组合。 τ σ 14. 图示两端铰支压杆的截面为矩形。当其失稳时。 A. 临界压力 Pcr＝π2EIy／l2，挠曲线位于 xy面内； B. 临界压力 Pcr＝π2EIy／l2，挠曲线位于 xz面内； C. 临界压力 Pcr＝π2EIz／l2，挠曲线位于 xy面内； D. 临界压力 Pcr＝π2EIz／l2，挠曲线位于 xz面内。 15. 结构的超静定次数等于。 A．未知力的数目； B．支座反力的数目； C．未知力数目与独立平衡方程数目的差数； D．支座反力数目与独立平衡方程数目的差数。

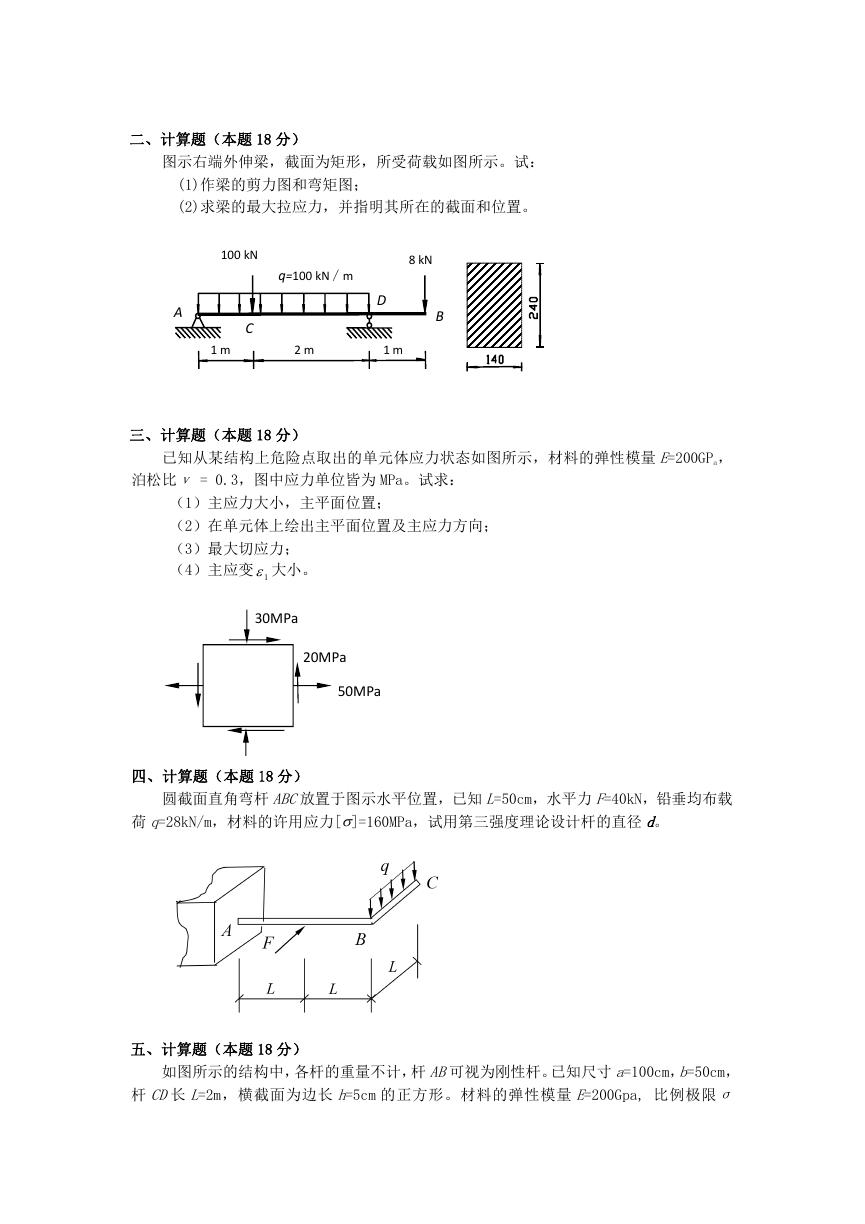
二、计算题（本题 18 分）图示右端外伸梁，截面为矩形，所受荷载如图所示。试： (1)作梁的剪力图和弯矩图； (2)求梁的最大拉应力，并指明其所在的截面和位置。 100 kN q=100 kN∕m A C 1 m 2 m 8 kN B D D 1 m 三、计算题（本题 18 分）已知从某结构上危险点取出的单元体应力状态如图所示，材料的弹性模量 E=200GPa，泊松比ν = 0.3，图中应力单位皆为 MPa。试求：（1）主应力大小，主平面位置；（2）在单元体上绘出主平面位置及主应力方向；（3）最大切应力；（4）主应变 1 大小。 30MPa 20MPa 50MPa 四、计算题（本题 18 分）圆截面直角弯杆 ABC放置于图示水平位置，已知 L=50cm，水平力 F=40kN，铅垂均布载荷 q=28kN/m，材料的许用应力[]=160MPa，试用第三强度理论设计杆的直径 d。五、计算题（本题 18 分）如图所示的结构中，各杆的重量不计，杆 AB可视为刚性杆。已知尺寸 a=100cm，b=50cm，杆 CD长 L=2m，横截面为边长 h=5cm 的正方形。材料的弹性模量 E=200Gpa, 比例极限σ

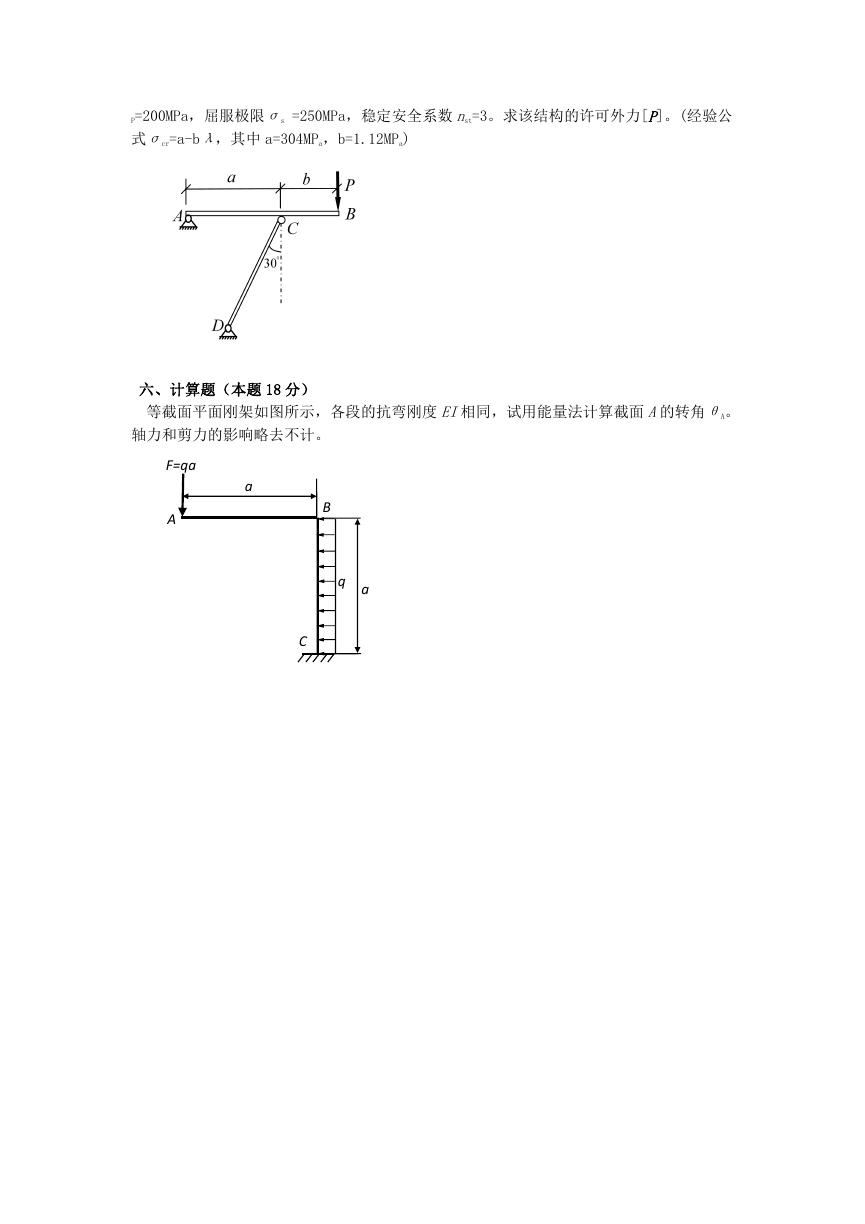
P=200MPa，屈服极限σs =250MPa，稳定安全系数 nst=3。求该结构的许可外力[P]。(经验公式σcr=a-bλ，其中 a=304MPa，b=1.12MPa) 六、计算题（本题 18 分）等截面平面刚架如图所示，各段的抗弯刚度 EI相同，试用能量法计算截面 A的转角θA。轴力和剪力的影响略去不计。 F=qa A a B q a C

分享到：

赞收藏

资料库

2015年云南昆明理工大学材料力学考研真题A卷.doc

相关推荐

考研

热门标签

最新资料