第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
论文研究 - 考虑风能和交互式负荷的电力系统多目标最优调度.pdf
Multi-Objective Optimal Dispatch Considering Wind Power and Interactive Load for Power System
Abstract
Keywords
1. Introduction
2. Interactive Load Modeling
3. Multi-Objective Optimal Statement
3.1. Problem Objectives
3.2. Problem Constraints
3.3. Optimal Dispatch Modeling
4. Proposed Approach
5. Simulation and Evaluation
6. Conclusion
Acknowledgements
References
Energy and Power Engineering, 2018, 10, 1-10
http://www.scirp.org/journal/epe
ISSN Online: 1947-3818
ISSN Print: 1949-243X
Multi-Objective Optimal Dispatch Considering
Wind Power and Interactive Load for Power
System
Xinxin Shi1,2,3, Guangqing Bao1,2,3*, Kun Ding4, Liang Lu4
1College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou, China
2Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou University of Technology, Lanzhou, China
3National Demonstration Center for Experimental Electrical and Control Engineering Education, Lanzhou University of
Technology, Lanzhou, China
4Key Laboratory of Wind Power Integration Operation and Control, Gansu Electric Power Corporation Wind Power Corporation
Wind Power Technology Center, Lanzhou, China
How to cite this paper: Shi, X.X., Bao,
G.Q., Ding, K. and Lu, L. (2018) Mul-
ti-Objective Optimal Dispatch Considering
Wind Power and Interactive Load for
Power System. Energy and Power Engi-
neering, 10, 1-10.
https://doi.org/10.4236/epe.2018.104B001
Received: March 6, 2018
Accepted: April 8, 2018
Published: April 11, 2018
Abstract
With the rapid and large-scale development of renewable energy, the lack of
new energy power transportation or consumption, and the shortage of grid
peak-shifting ability have become increasingly serious. Aiming to the severe
wind power curtailment issue, the characteristics of interactive load are stu-
died upon the traditional day-ahead dispatch model to mitigate the influence
of wind power fluctuation. A multi-objective optimal dispatch model with the
minimum operating cost and power losses is built. Optimal power flow dis-
tribution is available when both generation and demand side participate in the
resource allocation. The quantum particle swarm optimization (QPSO) algo-
rithm is applied to convert multi-objective optimization problem into single
objective optimization problem. The simulation results of IEEE 30-bus system
verify that the proposed method can effectively reduce the operating cost and
grid loss simultaneously enhancing the consumption of wind power.
Keywords
Wind Power, Interactive Load, Optimal Dispatch, Multi-Objective,
QPSO Models
1. Introduction
Wind power industry has been rapidly developed. Wind power generation
reached 241 billion kW∙h that has been 30% year-on-year growth accounting for
DOI: 10.4236/epe.2018.104B001 Apr. 11, 2018
1
Energy and Power Engineering
X. X. Shi et al.
DOI: 10.4236/epe.2018.104B001
4% of the total electricity generation in China. Among them, new energy in-
stalled capacity accounted for more than 30% of the total installed capacity of
the local power supply in Gansu, Ningxia, Xinjiang, Qinghai, which has shown
favourable prospects in reducing fossil energy consumption and pollutant emis-
sions [1]. However, the demand of electricity is influenced by variable factors,
such as weather, economy, laws, policies, electrical load conditions, and so on.
These factors make electric dispatch became a task. Especially, when the wind
power integrated into the main grid, the intermittent and stochastic nature of
such energy brings challenges to system dispatch. Therefore, usage of wind
power generation is of major importance in future power grids for economic
and environmental reasons. In recent years, the researches of academic experts
published which classified into two major categories, one is multi-objective dis-
patch modeling; another one is optimal dispatch solving technology. A stochas-
tic multi-objective optimal reactive power dispatch model is studied concerning
about load and wind power generation uncertainties, including real power losses
and operation cost of wind farms [2]. The objective function is implemented for
energy saving and emission-reduction [3]. The day-ahead multi-objective op-
timal dispatching model containing thermal power, hydro power, wind-power
and pumped storage units is given to minimize the total costs and CO2 emission
under multiple constraints. A fuzzy modeling for dynamic economic dispatch is
presented in [4], which could make the dispatch to reflect the willingness of de-
cision-makers and hereby adapt the random wind power output better. A mul-
ti-objective optimization algorithm based on the non-dominated sorting diffe-
rential evolution is used to solve the economic environmental dispatch stochas-
tic optimization model of power system connected with large scale wind farms
[5]. And a solution of optimal dispatch problem with a particle swarm optimisa-
tion based on multi-agent systems is presented in [6]. Optimal scheduling strat-
egy is considered only from the generation side above literature. In this paper,
the characteristics of interaction load and integration into the traditional sche-
duling model is discussed. The problem is formulated as a multi-objective op-
timal problem through simultaneous minimizing both system operational cost
and power loss. QPSO algorithm has been introduced to solve this problem. Fi-
nally, the system simulation is carried out with IEEE 30 nodes. The experimental
results verify the effectiveness of the proposed method, and have some certain
practical significance for power system optimal scheduling.
2. Interactive Load Modeling
1) Interactive load characteristics
2) Interactive load model
• Shiftable load
The dispatching center calculates the optimal power dispatching plan accord-
ing to the information provided by the intention chart which determine the op-
timal dispatch time of the load user and the shiftable load involved in shifting
2
Energy and Power Engineering
X. X. Shi et al.
the peak. Therefore, for the rth shiftable load, the decision variable is the start
variable
srU = ; If it starts at other times,
t
then
is the start time of the rth shiftable peak load [7] [8].
srU : If it starts in the t period, then
srU = ;
0
srt
1
t
t
The shift cost curve characterizes denotes the compensation price that the us-
er should obtain from the grid company after providing the shift service. The
mathematical description is as follows:
C
t
sr
=
sr
m t
(
m t
(
0
sr
sr
0
−
t
−
t
sr
0
)
)
−
m T
sr
sro
0
t
t
≤ <
>
t
t
sr
0
T
t
+
sr
sr
0
0
t
t
≤ ≤
sr
0
sr
0
(1)
+
T
sr
0
t
where is
srC the peak cost of the rth shiftable peak load in the t period of the
srm is the compensation factor for the load of the rth shiftable peak load
peak;
that is determined by the load control agreement signed from the user and the
power company in advance;
0srT are the number of the original power
load start time and load duration before the peak which belong to known para-
meters.
and
0srt
• Interruptible load
Users through the auction to declare interruptible capacity and compensation
prices as well as the dispatch center by calculating the optimal power generation
scheduling program to determine the interruptible users and the optimal capac-
ity. Dispatching the hth interruptible load of the user’s compensation cost as
shown in Equation (4) [9]
0
Ih
=
t
Ih
C
t
t
C P I
Ih Ih
(2)
0IhC is the unit to reduce load costs of the hth interruptible load in the
IhP is the load reduction of the hth interruptible load in the t period ;
is variable dispatch for interruptible load. The interruptible load was
where
contract;
t
and
IhI
whether to dispatched basing on
t
IhI = and
1
t
IhI = .
0
t
3. Multi-Objective Optimal Statement
The problem of economic power dispatch with wind penetration consideration
can be formulated as a multi-objective optimal dispatch model. The two con-
flicting objectives, i.e., operating cost and system power loss, should be mini-
mized simultaneously while fulfilling certain system constraints. This problem is
formulated mathematically in this section.
3.1. Problem Objectives
• Objective 1: Minimization of operational cost
1min
C C
Gi
=
+
C
Wi
(3)
{
U a
[
i
t
Gi
+
t
b P
i Gi
+
t
c P
i
Gi
(
2
) ]
+
t
C
Ui
(1
−
U
t
1
−
Gi
)
+
C
t
Ri
}
(4)
C
Gi
=
cNT
∑∑
t
1
=
i
1
=
C
Wi
=
T
N
S
∑ ∑
(
t
1
=
j
1
=
C
t
Sr
+
N
I
∑
i
1
=
C
t
Ih
)
(5)
DOI: 10.4236/epe.2018.104B001
3
Energy and Power Engineering
X. X. Shi et al.
t
t
GiP ,
t
where T is the number of hours during system dispatching;
of generating units; and
of the ith generator in the period;
contrary,
spare costs and starting cost of the ith generator in the period;
represent the number of shiftable peak load;
removable peak load and the hth interruptible load in the t period.
CN is the number
GiU are the active output and the state variables
indicates a shutdown state. On the
t
UiC denote the
IN
t
IhC denote the cost of the rth
GiU = indicates that the generator set is on;
t
RiC ,
t
GiU =
t
SrC ,
SN ,
1
0
t
t
• Objective 2: Minimization of system power loss
The dispatch of interactive load will inevitably cause the change of power flow
distribution, which will have some influence on the system power loss. Thus, the
minimize of power loss is one goal of optimal dispatching. Here the use of
B-coefficient method to calculate the power loss [10].
min
C
2
=
T
K K
∑ ∑∑
(
t
1
=
i
1
=
j
1
=
t
t
P B P
i
j
i j
,
+
K
∑
i
1
=
t
B P
i
i
,0
+
B
0,0
)
(6)
where K is the number of system nodes;
which are the first term and the constant term of the coefficient; and
are active power of node i and j.
0,0B are the second term ,
t
jP
,0iB ,
,i jB ,
t
iP ,
3.2. Problem Constraints
• Constraint 1: Power balance constraint [11]
• Constraint 2: Spare constraints
• Constraint 3: Unit constraint
• Constraint 4: Interactive load constraint [12]
3.3. Optimal Dispatch Modeling
The objective of this model is to minimize the operating cost and the grid loss as
much as possible under all constraints. Therefore, when the operating cost and
the network loss are lower, the fitness value of the fitness function is greater.
Where the fitness function can be defined as [13]:
C
(
µ
i
)
=
1
2
C mC n
i
0
+
+
i
x
C C
i
C
C C
i
≤
<
>
x
C
i
C C
+ ∆
≤
i
x
C
+ ∆
i
x
(7)
m
( 2
= −
C C
i
∆ − ∆
x
2
C
i
−
1) /
∆ (8)
C
i
n
1
= −
C
2
x
−
C
x
2
C
i
−
1) /
C
∆
i
]
(9)
∆ − ∆
x
[( 2
⋅ −
C C
i
C C C
∆ =
i
−
i
(10)
x
iC is the ith objective function value;
xC is the ith objective function
iC∆ is the ith objective function added value. The fitness function
where
ideal value.
diagram is shown in Figure 1.
Thus, where the fitness index can be defined as:
µ
=
min
{
C
(
µ µ
C
(
1
),
}
)
2
(11)
DOI: 10.4236/epe.2018.104B001
4
Energy and Power Engineering
X. X. Shi et al.
Figure 1. Fitness function diagram.
where µ is the minimum value for all fitness functions.
The multi-objective problem is transformed into a single objective nonlinear
optimization problem that satisfies the fitness value of all constraints:
max
µ
. .s t C
1
C
C C
µ
+ ∆ ≤
1
1
C
C
≤
+ ∆
µ
2
C
+ ∆
1
C
+ ∆
2
2
(12)
2
4. Proposed Approach
In this paper, the quantum particle swarm optimization (QPSO) [14] is used to
solve the model, which is based on the particle swarm optimization (PSO) to
improve the formation. All particles in the population are treated as quantum
particles in the feasible solution. When updating the particle position, it mainly
considers the current local optimal position and global optimal position infor-
mation of each particle.
5. Simulation and Evaluation
In this study, a IEEE 30-bus system with 1-wind farm of grid-connected is used
to investigate the effectiveness of the model. The system configuration is shown
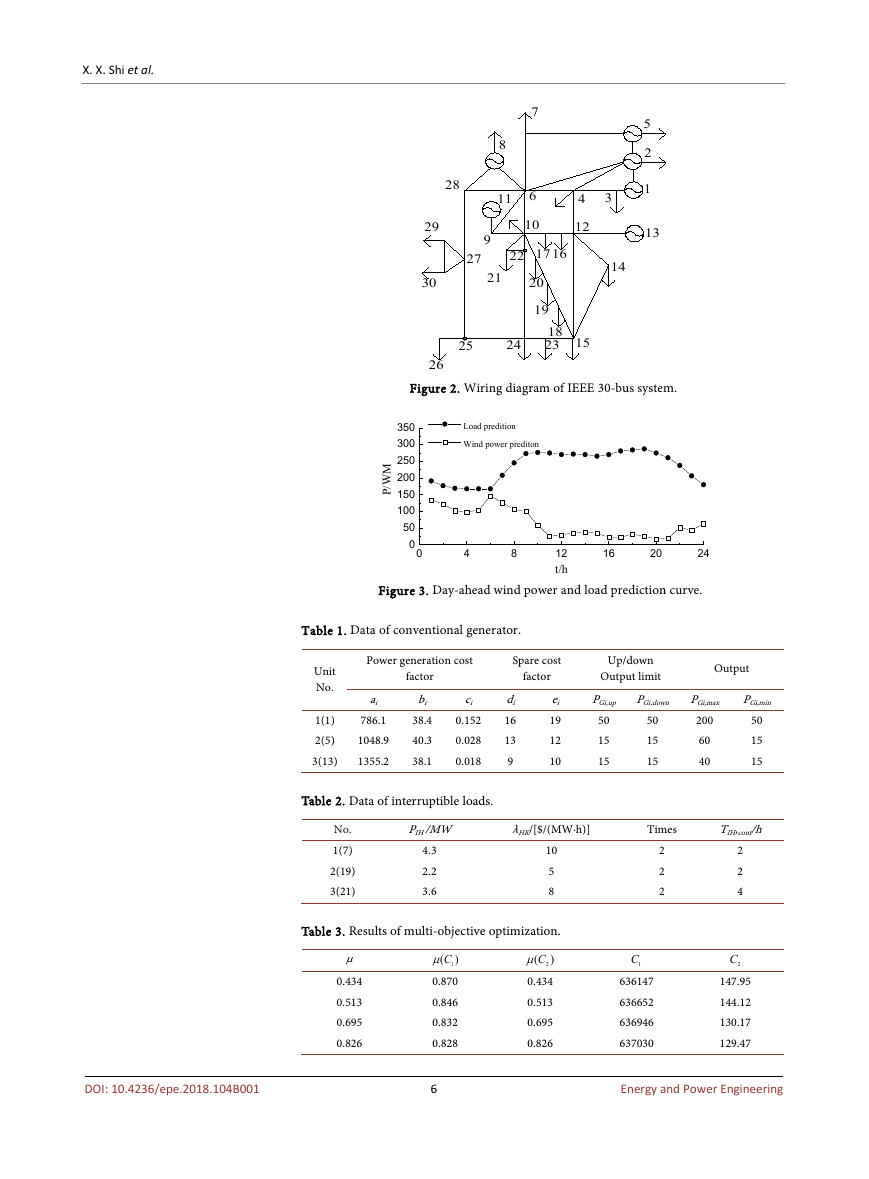
in Figure 2.
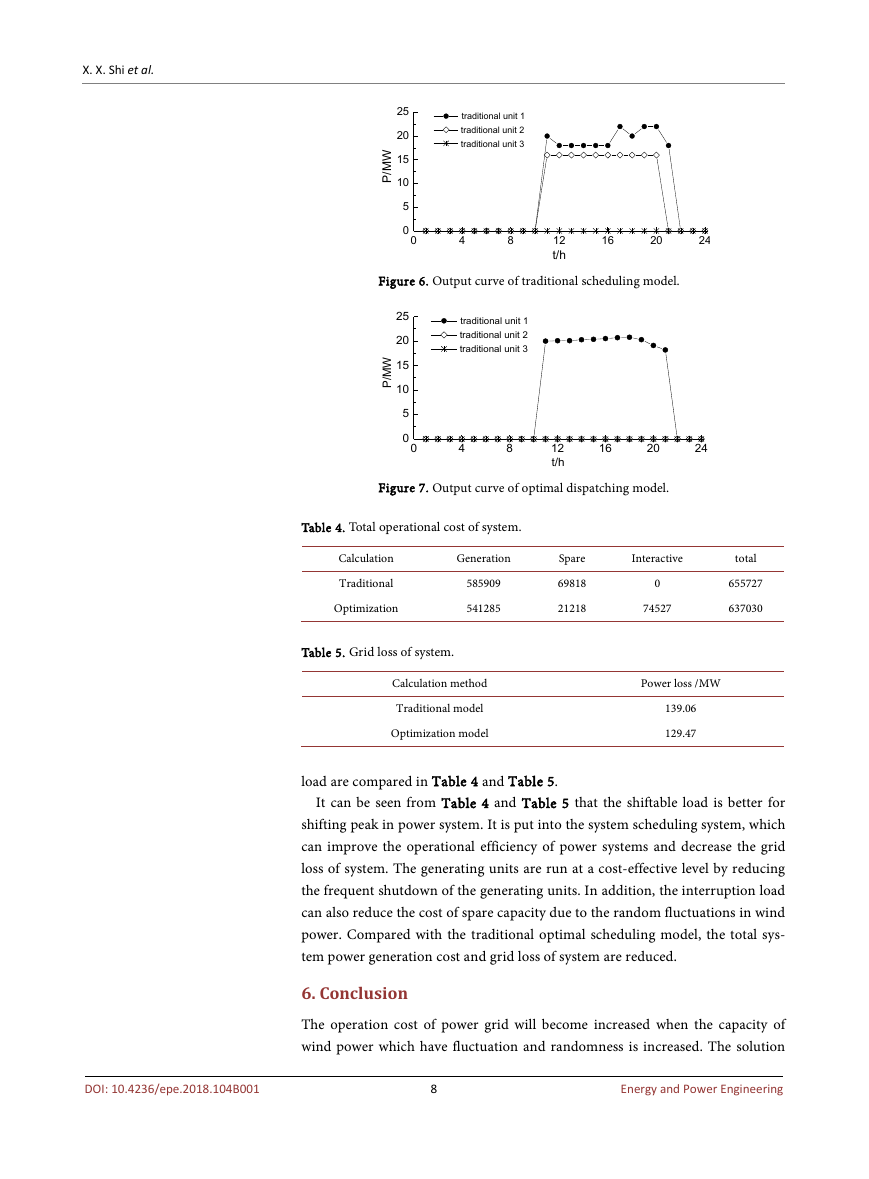
The system parameters including generator capacities, spare cost and fuel cost
coefficients are listed in Table 1.
The interruptable capacity, compensation price, interruptable times and dura-
tion for interruptible load are listed in Table 2.
1) There are 100 wind turbines in the wind farm with a total installed capacity
of 200 MW. Conventional unit positive and negative rotation standby demand
for the maximum unit capacity of 15%.
2) The particle size scale of QPSO algorithm is 100 and the maximum number
of iterations is 500.
3) The prediction curves and load forecast curves of the wind power during
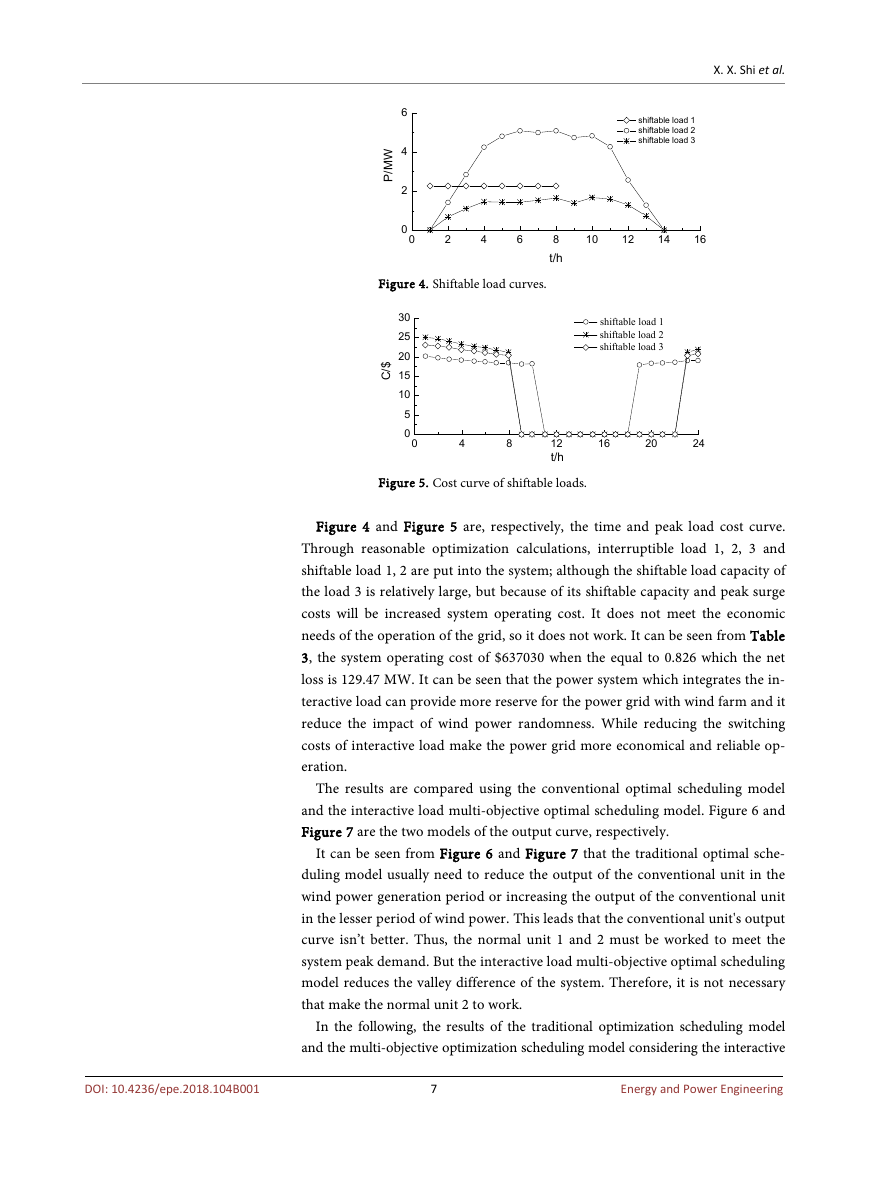
the last 24 hours are shown in Figure 3.
4) The willingness curve and the peak cost of the shiftable load are shown in
Figure 4 and Figure 5, respectively.
It can be seen from Figure 3 that there is obvious anti-peaking characteristic
of wind power and load side. The three interruptible loads of this example are at
nodes 7, 19, 21 in the interactive load respectively and where three shiftable
loads are at nodes 10, 12, 29.
5
Energy and Power Engineering
DOI: 10.4236/epe.2018.104B001
X. X. Shi et al.
8
11
28
29
30
9
27
21
7
6
10
22
1716
20
19
5
2
1
13
3
4
12
14
25
24
18
23
15
26
Figure 2. Wiring diagram of IEEE 30-bus system.
M
W
P
/
350
300
250
200
150
100
50
0
Load predition
Wind power prediton
0
4
8
12
t/h
16
20
24
Figure 3. Day-ahead wind power and load prediction curve.
Table 1. Data of conventional generator.
Power generation cost
Spare cost
factor
Up/down
Output limit
Output
ci
0.152
0.028
0.018
di
16
13
9
ei
19
12
10
PGi,up PGi,down PGi,max PGi,min
50
15
15
200
60
40
50
15
15
50
15
15
Unit
No.
1(1)
2(5)
3(13)
factor
bi
38.4
40.3
38.1
ai
786.1
1048.9
1355.2
Table 2. Data of interruptible loads.
No.
1(7)
2(19)
3(21)
PIH /MW
4.3
2.2
3.6
Table 3. Results of multi-objective optimization.
λHK/[$/(MW∙h)]
Times
TIH,cont/h
10
5
8
2
2
2
µ
0.434
0.513
0.695
0.826
)Cµ
1(
0.870
0.846
0.832
0.828
6
DOI: 10.4236/epe.2018.104B001
2
)Cµ
(
0.434
0.513
0.695
0.826
1C
636147
636652
636946
637030
Energy and Power Engineering
2
2
4
2C
147.95
144.12
130.17
129.47
X. X. Shi et al.
shiftable load 1
shiftable load 2
shiftable load 3
0
2
4
6
8
t/h
10
12
14
16
W
M
P
/
6
4
2
0
Figure 4. Shiftable load curves.
/
$
C
30
25
20
15
10
5
0
shiftable load 1
shiftable load 2
shiftable load 3
0
4
8
12
t/h
16
20
24
Figure 5. Cost curve of shiftable loads.
Figure 4 and Figure 5 are, respectively, the time and peak load cost curve.
Through reasonable optimization calculations, interruptible load 1, 2, 3 and
shiftable load 1, 2 are put into the system; although the shiftable load capacity of
the load 3 is relatively large, but because of its shiftable capacity and peak surge
costs will be increased system operating cost. It does not meet the economic
needs of the operation of the grid, so it does not work. It can be seen from Table
3, the system operating cost of $637030 when the equal to 0.826 which the net
loss is 129.47 MW. It can be seen that the power system which integrates the in-
teractive load can provide more reserve for the power grid with wind farm and it
reduce the impact of wind power randomness. While reducing the switching
costs of interactive load make the power grid more economical and reliable op-
eration.
The results are compared using the conventional optimal scheduling model
and the interactive load multi-objective optimal scheduling model. Figure 6 and
Figure 7 are the two models of the output curve, respectively.
It can be seen from Figure 6 and Figure 7 that the traditional optimal sche-
duling model usually need to reduce the output of the conventional unit in the
wind power generation period or increasing the output of the conventional unit
in the lesser period of wind power. This leads that the conventional unit's output
curve isn’t better. Thus, the normal unit 1 and 2 must be worked to meet the
system peak demand. But the interactive load multi-objective optimal scheduling
model reduces the valley difference of the system. Therefore, it is not necessary
that make the normal unit 2 to work.
In the following, the results of the traditional optimization scheduling model
and the multi-objective optimization scheduling model considering the interactive
7
Energy and Power Engineering
DOI: 10.4236/epe.2018.104B001
X. X. Shi et al.
DOI: 10.4236/epe.2018.104B001
25
20
15
10
W
M
P
/
5
0
0
traditional unit 1
traditional unit 2
traditional unit 3
4
8
12
t/h
16
20
24
Figure 6. Output curve of traditional scheduling model.
25
20
15
10
W
M
P
/
5
0
0
traditional unit 1
traditional unit 2
traditional unit 3
4
8
12
t/h
16
20
24
Figure 7. Output curve of optimal dispatching model.
Table 4. Total operational cost of system.
Calculation
Traditional
Optimization
Generation
585909
541285
Spare
69818
21218
Interactive
0
74527
total
655727
637030
Table 5. Grid loss of system.
Calculation method
Traditional model
Optimization model
load are compared in Table 4 and Table 5.
Power loss /MW
139.06
129.47
It can be seen from Table 4 and Table 5 that the shiftable load is better for
shifting peak in power system. It is put into the system scheduling system, which
can improve the operational efficiency of power systems and decrease the grid
loss of system. The generating units are run at a cost-effective level by reducing
the frequent shutdown of the generating units. In addition, the interruption load
can also reduce the cost of spare capacity due to the random fluctuations in wind
power. Compared with the traditional optimal scheduling model, the total sys-
tem power generation cost and grid loss of system are reduced.
6. Conclusion
The operation cost of power grid will become increased when the capacity of
wind power which have fluctuation and randomness is increased. The solution
8
Energy and Power Engineering
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
