论文研究 - 3d过渡和稀土金属的红外极化率.pdf-资料库

Journal of Modern Physics, 2018, 9, 287-301 http://www.scirp.org/journal/jmp ISSN Online: 2153-120X ISSN Print: 2153-1196 Infrared Polarizabilities of 3d-Transition and Rare-Earth Metals Kofi Nuroh Department of Mathematical Sciences, Kent State University, Salem, OH, USA How to cite this paper: Nuroh, K. (2018) Infrared Polarizabilities of 3d-Transition and Rare-Earth Metals. Journal of Modern Phys- ics, 9, 287-301. https://doi.org/10.4236/jmp.2018.92020 Received: December 31, 2017 Accepted: January 21, 2018 Published: January 24, 2018 Copyright © 2018 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). http://creativecommons.org/licenses/by/4.0/ Open Access 4.0 sr = Abstract A transition or rare-earth metal is modeled as the atom immersed in a jellium at intermediate electron gas densities specified by . The ground states of the spherical jellium atom are constructed based on the Hohenberg-Kohn- Sham density-functional formalism with the inclusion of electron-electron self-interaction corrections of Perdew and Zunger. Static and dynamic polari- zabilities of the jellium atom are deduced using time-dependent linear response theory in a local density approximation as formulated by Stott and Zaremba. The calculation is extended to include the intervening elements In, Xe, Cs, and Ba. The calculation demonstrates how the Lindhard dielectric function can be modified to apply to non-simple metals treated in the jellium model. Keywords Infrared, Polarizability, Jellium, Transition Metals, Rare-Earth Metals, Electron Self-Interaction Correction ( )α ω and its corresponding static value, 1. Introduction ( )0α The dynamical polarizability, for metals, have been investigated theoretically by mainly using aggregate of par- ( )0α has been shown to have an ano- ticles to mimic the metal. In particular, malous enhancement over its classical expected value of , where R is some characteristic radius of the metallic particle. In 1965, Gor’kov and Eliash- berg (GE) [1] introduced the idea of exploring the electronic excitations of small metallic particles based on phenomenological temperature-dependent statistical mechanics. With this concept they provided an explanation to the anomalous ( )0α . This insight generated interest in the physics of small enhancement in metallic particles and similar investigations ensued thereafter that exploited other theoretical methods. In general, these theoretical approaches may be classified ( ) 0 α = 3 R DOI: 10.4236/jmp.2018.92020 Jan. 24, 2018 287 Journal of Modern Physics

K. Nuroh into three grouping: those based on GEs original concept [2]-[15], those that rely on random phase approximation (RPA) and its variants [16] [17], and those that use self-consistent density-functional ideas [18]-[23]. ,nl and , (with l α ε= We utilize the following model as a means of mimicking the medal. A transi- tion or a rare-earth metal atom is immersed in a uniform electron gas of density sr , namely, the jellium model. The ground state of the spherical prescribed by jellium atom consisting of the discrete core levels and the continuum valence states are determined using the density functional prescription of Perdew and Zunger [24]. Since the prescription includes correction for electron self-interactions, it would provide a more accurate account of electron-electron interactions. A Thomas-Fermi pseudopotential has been used as the external potential to de- termine the initial density of the system. This serves as input to the Hohenberg- Kohn-Sham density-functional scheme [25] [26] to be described in Section II. Once the self-consistent complete set of energies { }ασε and wavefunctions { } ( ) σ= ± ) are determined, they are subjected to ασψ r a time-dependent linear density approximation (TDLDA) methods [27] [28] [29] [30], that have been so successfully used to determine the polarizability of sys- tems possessing spherical symmetry. The spherical jellium model is a crude one; nonetheless, calculations based on this model would serve as a first approxima- tion for more realistic calculations that should have to incorporate the transla- tional symmetry of the solid, especially in the transition metal atoms where the itinerant character of the valence states are crucial for many metallic properties. In the jellium model, the response of the interacting electron gas to an exter- ( ) ,ε ωq nal potential . If the external potential is weak, linear response theory may be invoked leading ( ) ,P ωq to a complex polarization function . Further, if the lowest term contri- ( ) ( ) ) ( ) P ωq ,P ωq , , ω = bution to , namely, ) ( ) ) ( ,ε ωq ε ω ε ω + is proportional to , where 1 1 ( q The Lindhard expression for this quantity is given in, e.g., Fetter and Walecka is retained, then we get ( ) ( ) P ωq leads to a complex dynamic dielectric function RPAε . ) ( ,φ ωq 1 2 q q ( , , i 2 , 1 1 [31] as Re P 1 ( ) ( q ) , ν = 2 mk 2  F ⋅ 1 4π 2 1 − +      1 q 2   1   −    ν q − 2 q 2        ln 1 1 + − ( ν ( ν q q − − q q ) ) 2 2 +  1 1  q 2   −    ν q + 2 q 2        ln 1 1 + − ( ν ( ν q q + + q q ) ) 2 2      q FE and ν ω= ) are used, then the input frequency ω is in rydbergs. Since where the dimensionless energy parameter ν and momentum parameter q . If atomic units ( 2e m= are respectively given by = ( ) ( ) 1 P ωq , 1= is proportional to the absorption probability for transferring the four-momentum ) ( ,ωq to the electron gas, we expect this quantity to be proportional to ( Imα ω for some fixed q . In the above, 0α ω is the non-interacting com- )α ω is its interacting counterpart. plex frequency-dependent polarizability, and q k ( ( Im = ) ) F 0 DOI: 10.4236/jmp.2018.92020 288 Journal of Modern Physics

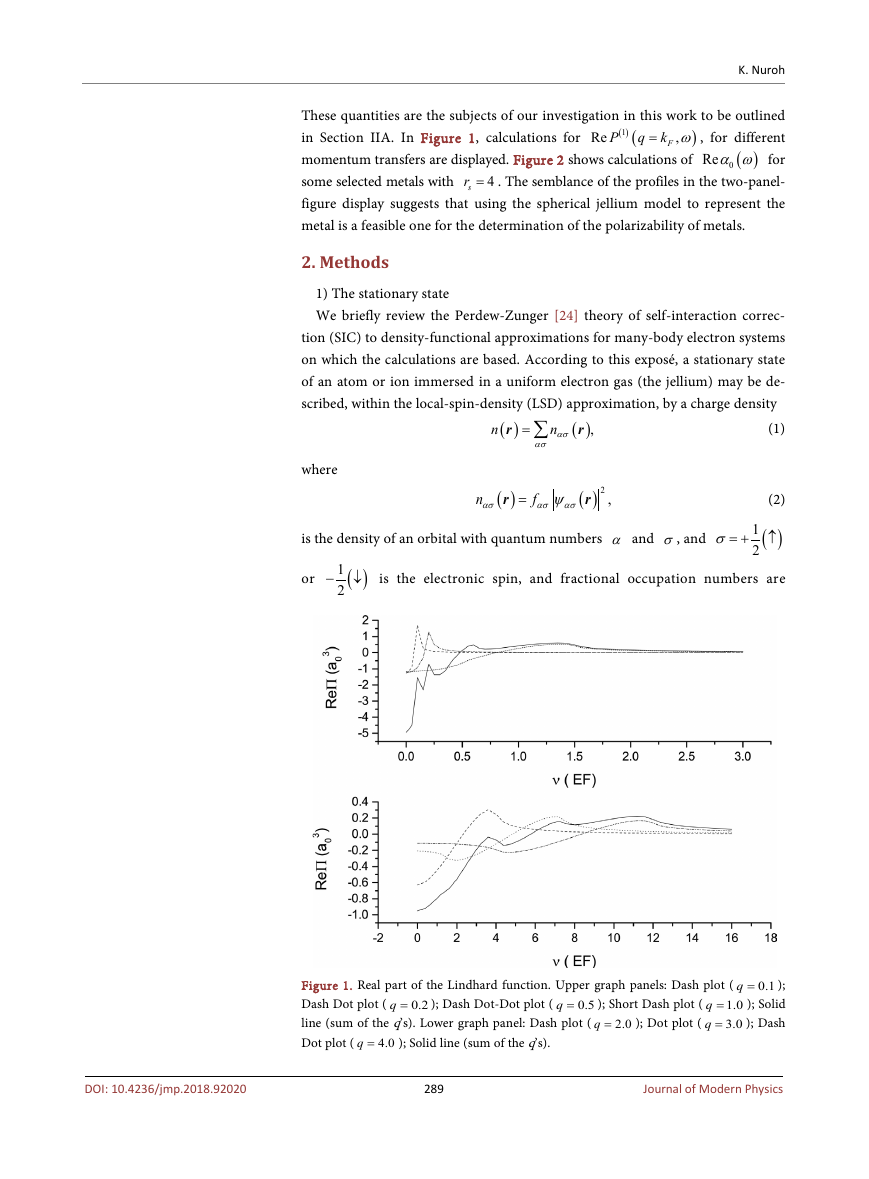
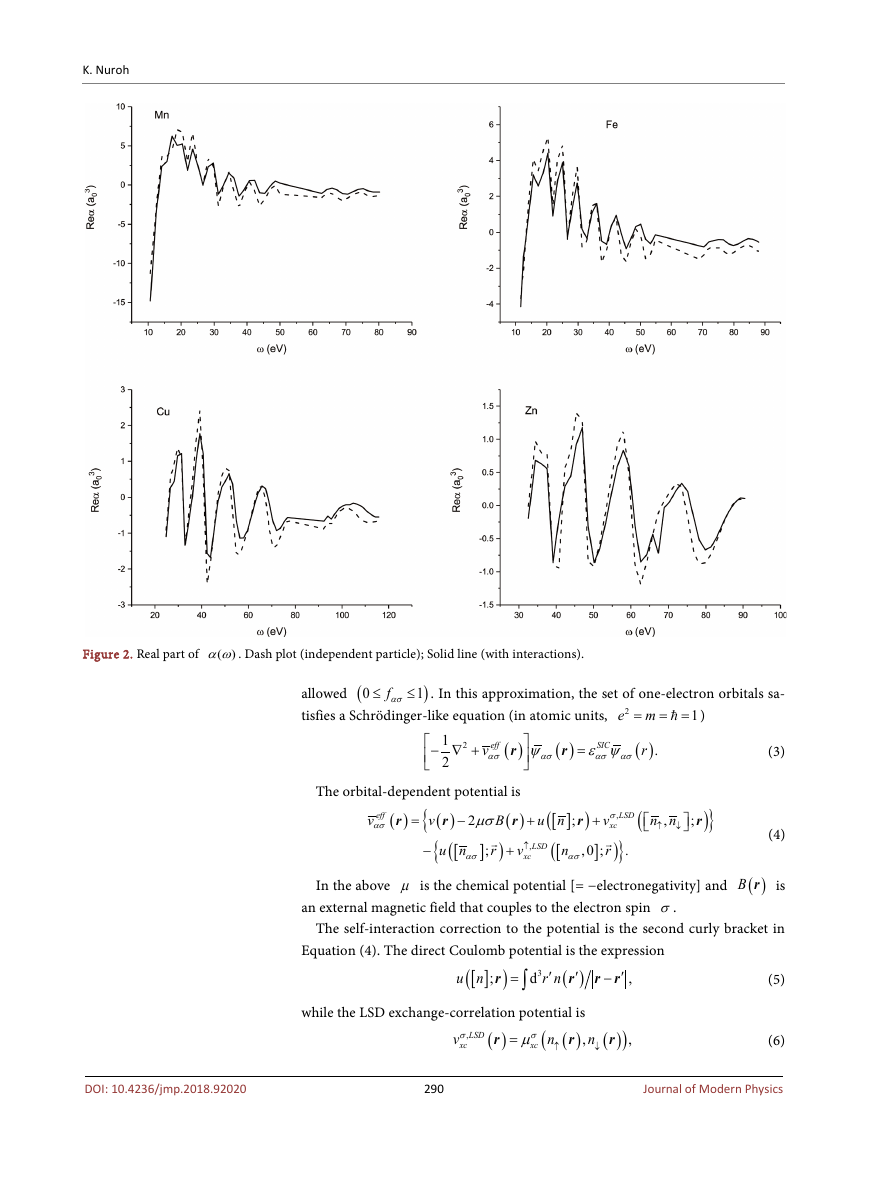
K. Nuroh These quantities are the subjects of our investigation in this work to be outlined ) in Section IIA. In Figure 1, calculations for , for different k ω= 0Reα ω for momentum transfers are displayed. Figure 2 shows calculations of sr = . The semblance of the profiles in the two-panel- some selected metals with figure display suggests that using the spherical jellium model to represent the metal is a feasible one for the determination of the polarizability of metals. ( ) ( Re ,F P q 4 ) ( 1 2. Methods 1) The stationary state We briefly review the Perdew-Zunger [24] theory of self-interaction correc- tion (SIC) to density-functional approximations for many-body electron systems on which the calculations are based. According to this exposé, a stationary state of an atom or ion immersed in a uniform electron gas (the jellium) may be de- scribed, within the local-spin-density (LSD) approximation, by a charge density (1) ( ), r ( ) = ∑r nασ n ασ where n ασ ( ) ασ ασψ=r f ( ) 2 , r or − 1 2 is the density of an orbital with quantum numbers α and σ, and ( ) ↓ is the electronic spin, and fractional occupation numbers are (2) ) ↑ σ= + ( 1 2 Figure 1. Real part of the Lindhard function. Upper graph panels: Dash plot ( Dash Dot plot ( 0.5 line (sum of the q’s). Lower graph panel: Dash plot ( Dot plot ( ); Short Dash plot ( ); Dot plot ( q = ); Solid line (sum of the q’s). ); Dash Dot-Dot plot ( q = q = q = q = q = 0.2 4.0 2.0 1.0 3.0 q = 0.1 ); ); Solid ); Dash DOI: 10.4236/jmp.2018.92020 289 Journal of Modern Physics

K. Nuroh Figure 2. Real part of )αω . Dash plot (independent particle); Solid line (with interactions). ( In the above µ is the chemical potential [= −electronegativity] and an external magnetic field that couples to the electron spin σ. The self-interaction correction to the potential is the second curly bracket in Equation (4). The direct Coulomb potential is the expression ( [ ] u n ; r ) d 3 r n′ ( ′ r ) = ∫ r − ′ r , (5) while the LSD exchange-correlation potential is ( ) r n , ↓ ( σµ ↑ n xc ( ) =r , σ v xc LSD ( ) r ) , (6) DOI: 10.4236/jmp.2018.92020 290 Journal of Modern Physics allowed ( tisfies a Schrödinger-like equation (in atomic units, ) 1 ≤ . In this approximation, the set of one-electron orbitals sa- fασ≤ 0 ( ) r = SIC ε ψ ασ ασ ασ 2 e m= ( ) r . = = 1 ) (3)    eff v ασ ( ) r 21 2 − ∇ +  ψ   The orbital-dependent potential is ( ) r v + { ( ) r v − { ( [ u n − B 2 µσ  ) ] r ( ) r eff v ασ , ↑ xc ασ = + ; LSD ( r ; ( [ u n ( [ ] n ασ ) + ] ,0 ; LSD , σ v xc  r } ) .   n n , ↓ ↑   ; r } ) (4) ( )B r is

K. Nuroh ( xcn ε ↑   )   ) ∂ ( xc n n , ε ↑ ↓ σµ is given by the functional derivative . The ex- and xc pression is the exchange-correlation energy per particle of an elec- tron gas with the spin density ↓ . This makes it possible for the homogene- ous system to be folded into calculations for the inhomogeneous systems like atoms and ions. For the detailed construct of the expressions in this section, the interested reader is referred to the original formulation in Reference [24]. n n , ↓ ,n n↑ nσ ∂ , { { n ↑ n ↓ ( ) r } ( ) r and the spin orbital densities An iterative procedure is used to solve Equations (1)-(4). First, an initial guess } ( ) nασ r is made for the spin instead of using Equations ((1) and (2)). Then Equations ((3) and (4)) are solved using a direct predictor-corrector numerical integration. Thereafter, Equations (1)-(4) are successively solved until self-consistency is achieved with a relative accuracy of 10−6 in both sets of densities, or a relative accuracy of 10−6 in energy, whichever occurs first. The orbital densities are first sphericalized before evaluating the potential and the total energy. (A bar over any variable in an expression or equation signifies that the self-consistent value is used in eva- luating it.) After a self-consistent set of orbitals is obtained, the total energy within the LSD may be computed as E tot { } ( ) ασψ r } ( ) nασ r SIC f ασ ασ ε { = ∑ ασ = f ασ ∑ ασ − ψ ασ ασ  ψ   ( [ u n ; ασ 1 2 ] r − ∇ + 2 v ) + v , ↑ xc + ( ) r − ( [ B 2 µσ ] ,0 ; n ασ ( ) r ) r LSD ψ ασ ( [ u n } . ] ; r ) LSD + , σ v xc (   n n , ↓ ↑   ; r ) ψ ασ (7) Again, the more prescribed calculational details are left for the interested reader to consult with the original paper of Reference [24]. n n ↓= α = 2) Linear response and polarizability In Section IIA the stationary states are set up to perform spin-polarized calcu- lation. From now onward, we drop the bars on quantities in Section IIA. We set = so that the calculation is now spin non-polarized. Further, we drop n ↑ the spin label σ and take the set of quantum labels { } { }nl . According to the theory of linear response, if an arbitrary system of electrons is perturbed by ( an external potential in its density from its ground state value ( n r ( ) ,χ ω′ (8) is the frequency-dependent response function for the interacting electron system. On the other hand, if the density fluctuation is viewed as arising from an induced effective potential for the system, then it may equivalently be represented as ) δ ω ) extv ωr it induces a deviation ( ) ) = ∫ r d δ ω , 0n r given by ′ r r , , (9) is the non-interacting response function for the fermion Here 0 χ ( r r , ) ω′ , The quantity ( ) ′ χ ω ) ,nδ ωr ) ′ , ω ) ′ , ω ) ′ , ω = ∫ v ext r r , r r , ′ 0 χ v eff r d n ( ( ( ( r r r ( , , . system, and the effective potential v eff ( ) , ω r = v ext ( ) , ω r + d ∫ ( ) effv ωr , is given by ( ) r n , δ ω ( ′− r r r d ′ xc + ∫ v ′ ′ r r r , ′ ) ) , δ ω n ′ , ( r (10) DOI: 10.4236/jmp.2018.92020 291 Journal of Modern Physics

K. Nuroh with v ′ xc ( r r , ) ′ = [ ] 2 E n δ xc ( ) ( r r n n δ δ ′ ) n n = 0 ( ) r , (11) n ( ) r ( ) r . A popular approximation to where it is considered that the exchange-correlation energy is the local density approximation (LDA) in which is simply taken as a function of the density, and Equation (11) be- comes ( ) r nδ xcv′ = + n 0 v ′ xc ( r r , ′ ) = v d ( ) n n xc d      (  δ  r ( ) 0 n n = r − ′ r ) . (12) The response function is an embodiment of all possible excitations from the }, ( ) jϕ jε will be presumed to be solutions to the Kohn-Sham equ- { rϕ ε . The eigenfunctions { rψ ε to excited states ( ) } , j j i ground state i and eigenenergies ations    − ∇ + 21 2 v eff ( ) r    ϕ j ( ) r = εϕ j j ( ) r , (13) n ( ) ϕ= ∑r j j ( ) 2, r (14) ( ) , r   ( )φ r is the electrostatic Hartree potential and ( ) r ( ) r φ= v eff + n   v xc where correlation potential. (15) xcv is the exchange- ( ) r  n  Following the approach of Reference [28], the non-interacting response func- tion may be expressed in terms of retarded Green’s function ε ω ψ ψ i i ψ ψ   i ) ′ , ω ( ) r ( ) r ′ r r , ∑ r r , 0 χ G = + + 2   ( ) ( ) ( r , ′ i i i occ , ( E′ G , ( ) r G r r , , r r , ( ) as ) ε ω − i 0 χ ( r r , ) ′ , ω = 2 ∑ i occ ,  ψ ψ  i ( ) r ∗ i ( ′ r ) G ( ′ r r , , ∗ ε ω ψ ψ i i + + ( ) r ) i ( ′ r ) G ( ′ r r , , ) ε ω i −   (16) where the summation is over the occupied states and ( ) ( ) ′ ∑ r r ϕ ϕ j j i E ε δ − + r r , G E = ′ , ( ) j j (17) Rather than using Equation (17) to determine the non-interacting susceptibil- ity in Equation (16), the retarded Green’s function can be directly obtained as the solution to the differential equation of Equation (13), ( δ , (18) − ∇ + E G ( ) r r r , = − E − − ′ , ( ) ) r r ′ effv    21 2    with the appropriate outgoing wave boundary conditions. 3) Response function with spherical symmetry Since we are dealing with a spherical jellium atom, it becomes convenient to work in spherical harmonics and write ( χ l ) ′ , ω = ∑ r r , 0 χ ( lm r r , ) ′ , ω Y lm ( ) ˆ ∗ r Y lm ( ′ ˆ r ) (19) DOI: 10.4236/jmp.2018.92020 292 Journal of Modern Physics

and G ( r r , ) ′ , ω = ∑ lm G r r , ( l K. Nuroh ) ′ , ω Y lm ( ) ˆ ∗ r Y lm ( ′ ˆ r ) . (20) The application of a uniform frequency-dependent electric field )ωE ( to the spherical atom corresponds to an external potential l ∑ ( ) ω ( ) ω ) , ω r ⋅ = v ext E E = ( r r + 4π 3 m l =− ( ˆ ( ) ˆ r Y E ∗ lm ) (21) Y lm If Equations ((20) and (21)) are substituted into Equation (16), only the dipo- couples to the external perturbation Equation (21) and lar component ( the non-interacting dipolar response function is )1l = 0 χ 1 = R n l i ) ′ r r , , ω ∑ ( 1 2π i occ , {  l G ×  i l i { l G i l i + ( 1 − 1 − ( ) r R n l i i i ′ r ( ) } ) ε ω i } ) + ε ω i + − , ′ r r , ( ′ r r , , l l { ( + { ( l l + G l i ) 1 ) G 1 l i + 1 + ( 1 + (22) ′ r r , ( ′ r r , , , + } ) ε ω i } )  ε ω  i − where ( ) ψ =r i R n l i i ( ) r Y l m i i ( )ˆ r . (23) From Equation (17) the harmonic component representation of the retarded Green’s function becomes G r r E ′ , , ( l ) = δ l l , j ∑ j 1 rr ′ u ( ) r u ε − n l j j n l j j + ) ( ′ r i δ n l j j E , (24) ( ) r ϕ = ( ) u r j j . But as has been remarked earlier, the and we have written daunting task of performing the summation over single-particle radial orbitals can be circumvented since from Equation (18), is a solution to the inhomogeneous radial differential equation lG r r E′ , ( ) , r −    1 d 2 r r d 2    2 r d r d    + ( l l 2 ) 1 + 2 r + v eff ( ) r − E G r r E ′ , , l (    ) = − 1 2 r ( δ r − ′ r ) , (25) , ) ( lG r r E′ , which satisfies the appropriate boundary conditions at the origin and at infinity. Following earlier observations [28], if E corresponds to a bound state energy then can be expressed in terms of solutions to the radial homoge- neous equation at energy 2 d r d 2 2 E k= ( ) l l 1 + 2 r . (26) ( ) r ( ) r v eff u lk − + + − = 2 0 : k 2 2       The harmonic component Green’s function is then given by G r r , ( l ) ′ , ω = 2 , ( )  1 φ χ  lk lk   W ⋅ ( )1 φ χ lk lk ( ) r ′ rr . (27) DOI: 10.4236/jmp.2018.92020 Here ( ) ( ) 1 rχ lk is the solution of Equation (26) that behaves asymptotically for 293 Journal of Modern Physics

K. Nuroh 1 ) lrh ( ) ( ( ) kr and lk rφ is the solution which is regular at the origin; r → ∞ as W refers to the Wronskian of the two solutions. If E does not correspond to a ( ) lk rφ bound state energy, Equation (27) is further simplified by normalizing  such that it behaves asymptotically as  . In this case ) lG r r ω′ becomes γ h  l ( ) ( ( ) ( kr kr h l + ) ) ( r , , 1 2 where R r k ; l ( ) φ= lk ( G r r , l r and ) , ω R l = − ( ) ( ( ) ( ) ikR r k R l ( ) ( ) 1 r χ= lk l k r ; ( ) ; 1 1 ( ) r , (28) ′ r k ; ) r . For the spherical jellium atom, the induced density can be expressed as ) δ ω α ω ω α ω = − E n ( ( ) ( ) ( ) r r r r , , , 4π 3 + l ∑ m l =− ( ˆ ( ) ˆ r Y E ∗ lm ) Y lm . (29) Putting this result in Equation (9) using Equation (10) leads to a linear ,rα ω as ( integral equation for the position-dependent polarizability ) ) α ω ( r , = − + + ∞ ∫ 0 ∞ ∫ 0 ∞ ∫ 0 ′ ′ 3 0 r r d χ 1 ( r r , ) ′ , ω ′ ′ r r d 2 ′ ′ r r d 2 ∞ ∫ 0 ∞ ∫ 0 ′′ ′′ r r d 2 0 χ 1 ( r r , ) ′ , ω ′ Y r r , 1 ( ′′ ) ) α ω ′′ , ( r , (30) ′′ ′′ r r d 2 0 χ 1 ( r r , ) ′ , ω v ′ xc ,1 ( ′ r r , ′′ ) ) α ω ′′ , ( r where ( Y r r , l ) ′ = 4π l 2 + 1 l r < l 1 + r > , (31) On the other hand, the application of the perturbation ) extv ωr ( , of Equation (21) gives rise to the induced dipole moment ) ( δ ω ( ) ω r r ,r p d = −∫ (32) in the spherical atom. Using Equation (29) we infer from Equation (32) that p ( ) ω ω E ) ( ⋅ = 2 E ( ) ω ∞ ∫ 0 r r d )( 3 α ω ( r , ˆ ˆ r E ⋅ )2 . (33) But the dynamic polarizability )α ω is related to the induced dipole mo- ( ment and the applied field as ( ) ) ω α ω ω = )ωp ( frequency-dependent polarizability as Substituting this value of E p ( ) ( . (34) into Equation (33) yields the complex ) α ω ( = ∞ 4π d ∫ 3 0 r r ) 3 α ω ( r , . (35) 3. Results and Discussion ) Imα ω , The prescription contained in Section IIC has been used to calculate the imaginary part of the polarizability, for the transition metals (TMs) and for the rare earth metals (REMs), including calculations for some intervening metals. ( 294 Journal of Modern Physics DOI: 10.4236/jmp.2018.92020

资料库

论文研究 - 3d过渡和稀土金属的红外极化率.pdf

相关推荐

开发技术

热门标签

最新资料