模拟退火算法解决旅行商问题实验报告附带c++程序.doc

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.19M 资料格式：doc 举报版权申诉

ranchonono-9299371-4744302543332374807.doc.pdf-第1页.png

第1页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第2页.png

第2页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第3页.png

第3页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第4页.png

第4页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第5页.png

第5页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第6页.png

第6页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第7页.png

第7页 / 共9页

ranchonono-9299371-4744302543332374807.doc.pdf-第8页.png

第8页 / 共9页

模拟退火算法解决旅行商问题

一、问题描述编写一个程序：旅行商问题（简记 TSP，亦称货郎担问题)：设有 n 个城市和距离矩阵 D=[dij]，其中 dij 表示城市 i 到城市 j 的距离，i，j=1，2 …n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。二、解决思路 1.实验采用模拟退火算法进行求解。模拟退火算法用 Metropolis 算法产生组合优化问题解的序列。并由 Metropolis 准则对应的转移概率 P 确定是否接受从当前解 i 到新解 j 的转移。 P(i=>j)= 1 f Exp( f )( j ) 当 f(j)<=f(i); 当 f(j)>f(j); )(  i t 开始时 t 值较大，可能接受较差的恶化解，随着 t 值的减小，只能接受较好的恶化解；当 t 值趋于零值时，就不再接受任何恶化解。这就使得算法可以跳出局部最优陷阱。其中，算法的精华在于对冷却表(cooling schedule)参数的控制，冷却表是一组控制算法进程的参数，用以逼近模拟退火算法的渐进收敛性态，使算法在有限时间内执行迭代过程后返回一个近似最优解。是影响模拟退火算法实验性能的重要因素，其合理选取是算法应用的关键。一个冷却表应当规定下述参数： ①控制参数 t 的初值 t0，初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。； ②控制参数 t 的衰减函数，应使 tk 的衰减以小为宜； ③控制参数 t 的终值 tf（停止准则），由停止规则决定，合理的停止准则既要确保算法收敛于某一近似解，又要使最终解具有一定的质量； ④Mapkob 链长 Lk，Lk 应选得在控制参数的每一取值上都能恢复平衡。 2.算法过程： ①从初始解 i0 出发，经过 L0 次解的变换（每次变换根据 Metropolis 算法求解），求得给定控制参数 t = t0 时问题的相对最优解。 ②减小控制参数 t 的值，对每个控制参数 t = tk，经过 Lk 次解的变换（每次变换根据 Metropolis 算法求解），求得在每一个控制参数 t 值下的问题的相对最优解。 ③在控制参数 t 趋于 0 时，最终求得的组合优化问题的整体最优解。 ④冷却表具体如下：城市个数：144 控制参数初值 t0=100 停止准则：连续 2 个 Mapkob 链中对路径无任何变动时即停止算法运行冷却进度表中的控制参数 t 的衰减函数：α(t)=0.9 * t Mapkob 链长：定长 20000 ○5 新解的产生：随机选择 2 个结点，交换路径中的这 2 个结点的顺序；随机选择 2 个结点，将路径中的这 2 个结点顺序逆转；随机选择 3 个结点 a, b, c.然后将结点 a 与 b 间的结点移位到结点 c 后面。

三、数据结构定义结构体 node 存储各城市变量坐标，并定义结构体类型变量 nodes。 struct node { int num; int x; int y; }nodes[CitiesNum]; 定义结构体 solut 为解的结构 struct solut { double length;//总长度 int path[CitiesNum];//路径 bool operator < ( const struct solut &other) const { return length < other.length; } }; 定义 solut 类型变量 best_solut 为全局最优解 solut best_solut = {INT_MAX, {0} }; generate 的辅助函数对象的类定义 class Genaration { private: int seed; public: Genaration (int _seed = -1): seed(_seed){} int operator() () { return seed += 1; } }; 实验平台：VC++6.0

四、算法流程选择初始路径 X0 确定初始温度 T0 当前路径 Xi=X0 当前温度 Ti=T0 从 Xi 的邻域中随机选择 Xj 计算 Xj 与 Xi 的路程差 △f=f (Xj)·f (Xi) Y Y 当前路径 Xi=Xj N N 当温度 Ti 下降 △f<=0 ? N Exp(-△f/Ti)> Random(0,1) N 跳出内循环 Y 跳出外循环 Y 输出结果 N

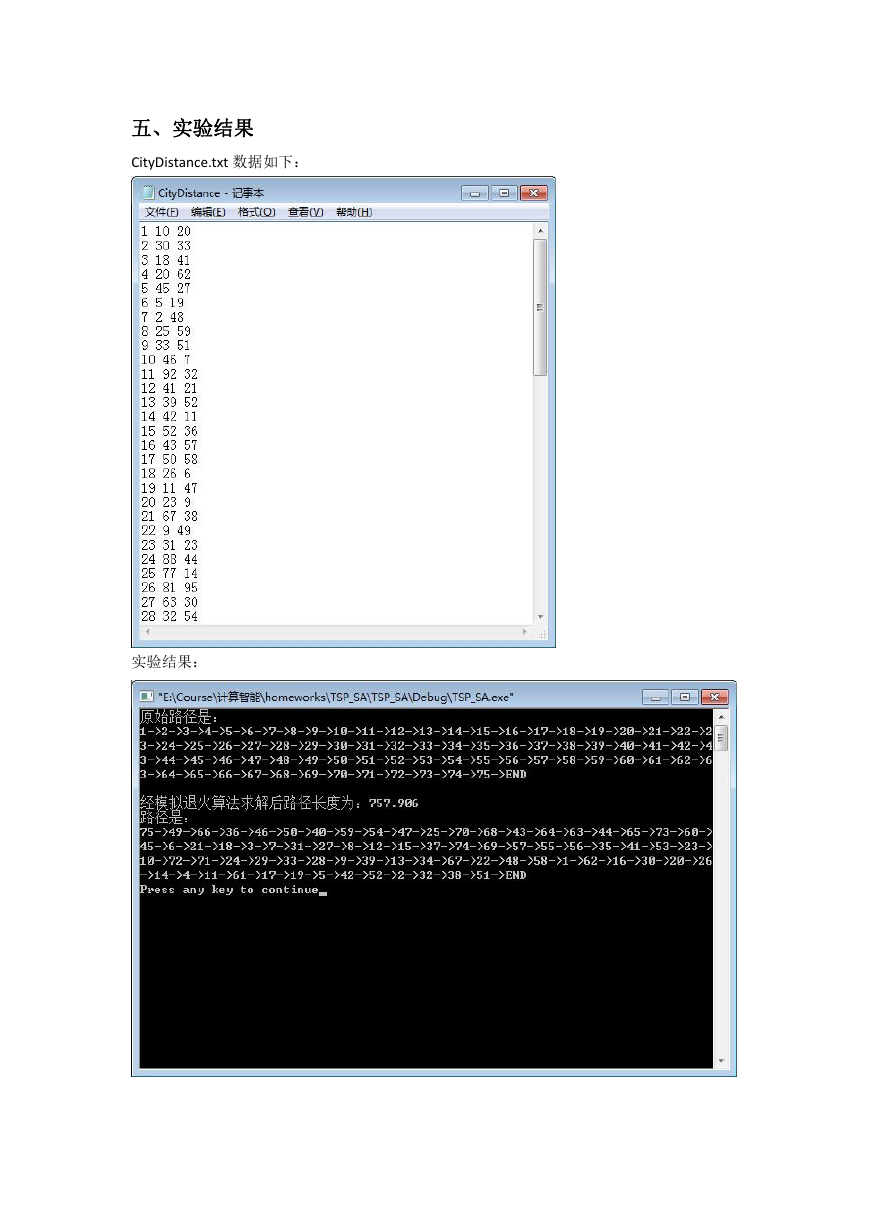
五、实验结果 CityDistance.txt 数据如下：实验结果：

六、附录代码 //========================================= //计算智能——2.模拟退火算法解决旅行商问题 //========================================= #include #include #include #include #include #include #include #include #include using namespace std; const int CitiesNum = 100; //城市数量 const double Speed = 0.9;//退火速度 const int INITI_T = 100;//初始温度 T const int L = 20000;//Mapkob 链长 double length_dis[CitiesNum][CitiesNum];//距离 //存储城市坐标 struct node { int num; int x; int y; }nodes[CitiesNum]; struct solut //定义解结构 { double length;//总长度 int path[CitiesNum];//路径 bool operator < ( const struct solut &other) const { return length < other.length; } }; solut best_solut = {INT_MAX, {0} };//最优解 void distance(); //存储城市距离 void SA_TSP(); void CalCulate_length(solut &p);//计算路径长度 //退火算法解决旅行商问题

void getNewSolution(solut &p);// 产生新解 bool Accept(solut &best_solut, solut &temp, double t);//Metropolis 准则接受新解 void print(solut &pr); void distance() //存储城市距离 { int i, j; ifstream in("CityDistance.txt"); for (i = 0; i < CitiesNum; i++) { //读入数据 in >> nodes[i].num >> nodes[i].x >> nodes[i].y; } for (i = 0; i < CitiesNum; i++) { length_dis[i][i] = (double)INT_MAX; for (j = i + 1; j < CitiesNum; j++) { length_dis [i][j] = length_dis[j][i] =sqrt( (nodes[i].x - nodes[j].x) * (nodes[i].x - nodes[j].x) + (nodes[i].y - nodes[j].y) * (nodes[i].y - nodes[j].y) ); } } } //stl 中 generate 的辅助函数对象 //功能：用指定函数对象产生的值去给容器指定范围内元素赋值 class Genaration { private: int seed; public: Genaration (int _seed = -1): seed(_seed){} int operator() () { return seed += 1; } }; void SA_TSP() { //模拟退火算法解决旅行商问题 srand(time(0)); int i = 0; double r = Speed; double t = INITI_T; const double t_min = 0.001; //温度下限 //选择初始路径 X0 solut temp;

generate(temp.path, temp.path + CitiesNum, Genaration(0)); random_shuffle(temp.path, temp.path + CitiesNum); CalCulate_length(temp); memcpy(&best_solut, &temp, sizeof(temp)); //停止条件未满足 while ( t > t_min ) { //赋值 //打乱顺序 for (i = 0; i < L; i++) { getNewSolution(temp); if(Accept(best_solut,temp, t)) else memcpy(&best_solut, &temp, sizeof(solut)); memcpy(&temp, &best_solut, sizeof(solut)); } t *= r; //退火 } return; } bool Accept(solut &best_solut, solut &temp, double t) { if (best_solut.length > temp.length) return true; //Metropolis 准则接受新解 else { 接受 if ((int)(exp((best_solut.length- temp.length) / t) * 100) > (rand() % 101) ) //以一定概率 { } return true; } return false; } void getNewSolution(solut &p) { // 产生新解 int i = rand() % CitiesNum; int j = rand() % CitiesNum; if (i > j) { int t = i; i = j; j = t;

分享到：

赞收藏

资料库

模拟退火算法解决旅行商问题实验报告附带c++程序.doc

相关推荐

课程资源

热门标签

最新资料