Iterated Soft-Thresholding Algorithm(谷鹄翔).pdf-资料库

问题描述背景介绍 . . . . . . . ISTA . . . . 实验结果 ISTA 总结 Iterated Soft-Thresholding Algorithm 报告人: 谷鹄翔中国科学院自动化研究所 March 19, 2012 报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

背景介绍 . . . . . . . ISTA . . . . 实验结果 ISTA 总结问题描述内容 .. .1 问题描述 .. .2 背景介绍 Majorization-Minimization 思想 The Landweber Iteration Soft-Thresholding .. .3 ISTA ISTA 算法与 l1 范数 ISTA 算法与 l2 范数 .. .4 实验结果 .. .5 ISTA 总结报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

问题描述背景介绍 . . . . . . . ISTA . . . . 实验结果 ISTA 总结问题描述在信号处理领域，比如去噪、反卷积、插值、超分辨率等，经常遇到线性求逆这一类经典问题： y = Hx + n (1) 其中 y 是我们观察到的信号， x 是待求的信号， n 为噪声， H 为系统响应，往往已知。当 H 不可逆或者噪声经 H1n 放大已经掩盖了真实信号 x，直接求逆往往不可行。报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

问题描述背景介绍 . . . . . . . ISTA . . . . 实验结果 ISTA 总结问题描述通常的处理方式： J(x) = D(y; Hx) + R(x) (2) 其中 D(y; Hx) = ky Hxk2 2: (3) (4) 今天我们只讲 p = 1 和 p = 2 时的求解算法，也就是我们经常遇到的 l1 和 l2 问题。 R(x) = kxkp: 报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

背景介绍 . . . . . . . ISTA . . . . 实验结果 ISTA 总结问题描述内容 .. .1 问题描述 .. .2 背景介绍 Majorization-Minimization 思想 The Landweber Iteration Soft-Thresholding .. .3 ISTA ISTA 算法与 l1 范数 ISTA 算法与 l2 范数 .. .4 实验结果 .. .5 ISTA 总结报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

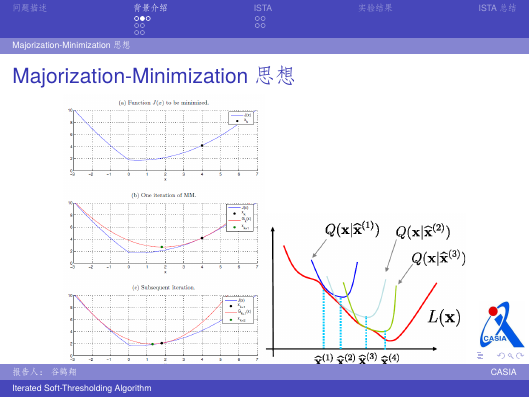
问题描述背景介绍 . . . . . . . ISTA . . . . Majorization-Minimization 思想 Majorization-Minimization 思想实验结果 ISTA 总结目标函数 J(x) 比较难优化的时候，我们往往寻找另外一个更容易优化的目标函数 G(x)，当 G(x) 满足一定的条件时， G(x) 的最优解能够无限逼近 J(x) 的最优解，这就是 MM 思想。 G(x) 应该满足的三个条件： 1 容易优化 2 Gk(x) J(xk) for all x 3 Gk(xk) = J(xk) 我们看看图解过程：报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

问题描述背景介绍 . . . . . . . ISTA . . . . Majorization-Minimization 思想 Majorization-Minimization 思想实验结果 ISTA 总结报告人: 谷鹄翔 Iterated Soft-Thresholding Algorithm . . . . . . CASIA

资料库

Iterated Soft-Thresholding Algorithm(谷鹄翔).pdf

相关推荐

行业

热门标签

最新资料