视觉SLAM-g2o简介及使用方法.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：2.44M 资料格式：pdf 举报版权申诉

weixin_41886779-10991142-16359647248922124854.pdf-第1页.png

第1页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第2页.png

第2页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第3页.png

第3页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第4页.png

第4页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第5页.png

第5页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第6页.png

第6页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第7页.png

第7页 / 共41页

weixin_41886779-10991142-16359647248922124854.pdf-第8页.png

第8页 / 共41页

文本预览

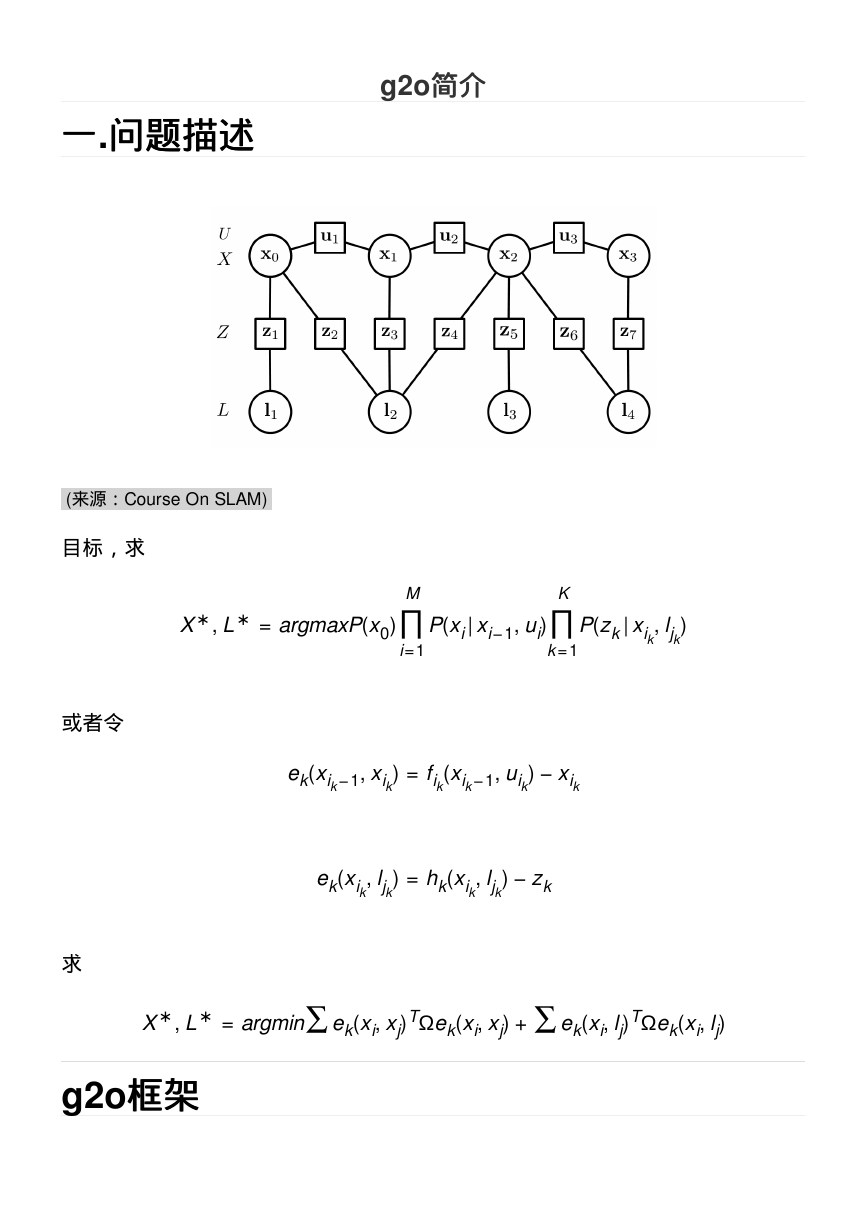
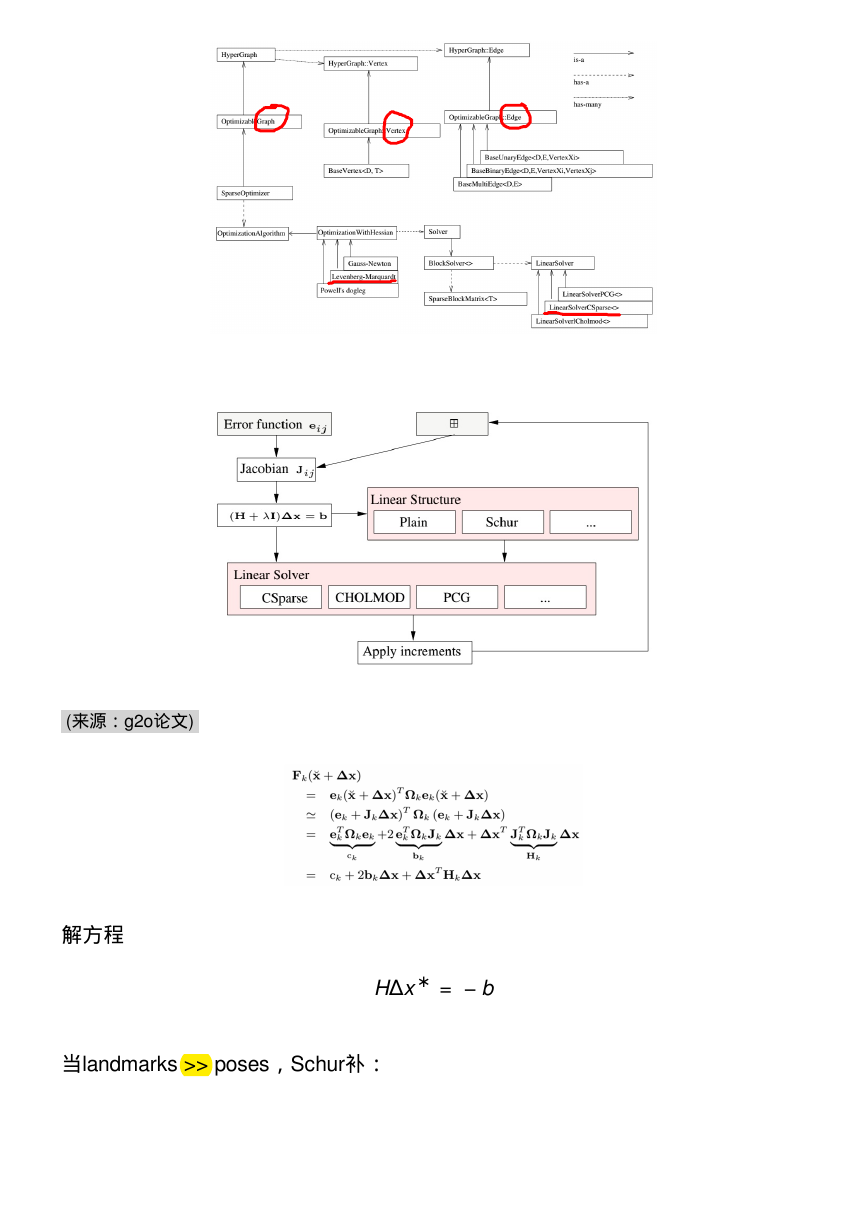
一一.问题描述问题描述 g2o简介简介 (来源：Course On SLAM) 目标，求 X ∗, L∗ = argmaxP(x0) M ∏ i=1 P(xi | xi−1, ui) K ∏ k =1 P(zk | xik , ljk ) 或者令求 ek(xik −1, xik ) = fik (xik −1, uik ) − xik ek(xik , ljk ) = hk(xik , ljk ) − zk X ∗, L∗ = argmin∑ ek(xi, xj)TΩek(xi, xj) + ∑ ek(xi, lj)TΩek(xi, lj) g2o框架框架

(来源：g2o论文) 解方程 HΔx ∗ = − b 当landmarks >> poses，Schur补： ( )

( Hpp Hpl HT pl Hll )( Δx ∗ p Δx ∗ l ) ( −bp −bl ) = ( 1 −HplH −1 ll 0 1 ) ( Hpp − HplH −1 ll HT pl HT pl )( Δx ∗ p Δx ∗ l ) 0 Hll ( = −bp + HplHllbl bl ) (Hpp − HplH −1 ll HT pl)Δx ∗ p = − bp + HplH −1 ll bl 两边分别乘以得到第一个方程：第二个方程 HllΔx ∗ l = − bl − HT plΔx ∗ p Jacobian和和Hessian的形式的形式 Jacobian矩阵：

Hessian矩阵：

代码代码一个简单的例子：一个简单的例子：tutorial_slam2d int numNodes = 300; Simulator simulator; simulator.simulate(numNodes, sensorOffsetTransf); /********************************************************************************* * creating the optimization problem ********************************************************************************/ // dimension of the pose and landmark vertices (-1 if variable) typedef BlockSolver< BlockSolverTraits<-1, -1> > SlamBlockSolver; typedef LinearSolverCSparse SlamLinearSolver; // allocating the optimizer SparseOptimizer optimizer; SlamLinearSolver* linearSolver = new SlamLinearSolver(); linearSolver->setBlockOrdering(false); SlamBlockSolver* blockSolver = new SlamBlockSolver(linearSolver); OptimizationAlgorithmLevenberg* solver = new OptimizationAlgorithmLevenberg(blockSolve r);

optimizer.setAlgorithm(solver); // add the parameter representing the sensor offset ParameterSE2Offset* sensorOffset = new ParameterSE2Offset; sensorOffset->setOffset(sensorOffsetTransf); sensorOffset->setId(0); optimizer.addParameter(sensorOffset); // adding the odometry to the optimizer // first adding all the vertices cerr << "Optimization: Adding robot poses ... "; for (size_t i = 0; i < simulator.poses().size(); ++i) { const Simulator::GridPose& p = simulator.poses()[i]; const SE2& t = p.simulatorPose; VertexSE2* robot = new VertexSE2; robot->setId(p.id); robot->setEstimate(t); optimizer.addVertex(robot); } cerr << "done." << endl; // second add the odometry constraints cerr << "Optimization: Adding odometry measurements ... "; for (size_t i = 0; i < simulator.odometry().size(); ++i) { const Simulator::GridEdge& simEdge = simulator.odometry()[i]; EdgeSE2* odometry = new EdgeSE2; odometry->vertices()[0] = optimizer.vertex(simEdge.from); odometry->vertices()[1] = optimizer.vertex(simEdge.to); odometry->setMeasurement(simEdge.simulatorTransf); odometry->setInformation(simEdge.information); optimizer.addEdge(odometry); // second add the odometry constraints } cerr << "done." << endl; // add the landmark observations cerr << "Optimization: add landmark vertices ... "; for (size_t i = 0; i < simulator.landmarks().size(); ++i) { const Simulator::Landmark& l = simulator.landmarks()[i]; VertexPointXY* landmark = new VertexPointXY; landmark->setId(l.id); landmark->setEstimate(l.simulatedPose);

landmark->setMarginalized(true); //Schur!!!!! optimizer.addVertex(landmark); } cerr << "done." << endl; cerr << "Optimization: add landmark observations ... "; for (size_t i = 0; i < simulator.landmarkObservations().size(); ++i) { const Simulator::LandmarkEdge& simEdge = simulator.landmarkObservations()[i]; EdgeSE2PointXY* landmarkObservation = new EdgeSE2PointXY; landmarkObservation->vertices()[0] = optimizer.vertex(simEdge.from); landmarkObservation->vertices()[1] = optimizer.vertex(simEdge.to); landmarkObservation->setMeasurement(simEdge.simulatorMeas); landmarkObservation->setInformation(simEdge.information); landmarkObservation->setParameterId(0, sensorOffset->id()); optimizer.addEdge(landmarkObservation); // add landmark observations } cerr << "done." << endl; /********************************************************************************* * optimization ********************************************************************************/ // dump initial state to the disk optimizer.save("tutorial_before.g2o"); // prepare and run the optimization // fix the first robot pose to account for gauge freedom VertexSE2* firstRobotPose = dynamic_cast(optimizer.vertex(0)); firstRobotPose->setFixed(true); // prepare and run the optimization optimizer.setVerbose(true); cerr << "Optimizing" << endl; optimizer.initializeOptimization(); optimizer.optimize(10); cerr << "done." << endl; optimizer.save("tutorial_after.g2o"); // freeing the graph memory optimizer.clear(); // destroy all the singletons

Factory::destroy(); OptimizationAlgorithmFactory::destroy(); HyperGraphActionLibrary::destroy(); 注： firstRobotPose->setFixed(true); Local Accuracy and Global Consistency for Efficient Visual SLAM If one proceeds exactly as explained above, one would realise that the matrix JTΛzJ is singular. This is caused by our decision to optimise over all poses T1, . . . , Tm and all points y1, . . . , yn. To get a better understanding of this, let us first consider bundle adjustment using a calibrated stereo rig; i.e. the observations z are three dimensional and the prediction function is zˆstereo. Now, let us assume that ¯T1, . . . , ¯Tm, ¯y1, . . . , ¯yn is the optimal solution to the BA minimization problem where the reprojection error of each point in each frame is minimal. It is important to note that all point measurements are relative, so that the solution does not depend on the absolute frame of reference. If we were now to apply a general rigid body transformation A ∈ SE(3) to all parameters, the reprojection error would still be minimal. In other words, A ¯T1, . . . , ¯Tm, A¯y1, . . . , A¯yn is another optimal solution to the problem. Therefore, we do have a six dimensional solution space, and thus we say that there is a gauge freedom of six dimensions. That is the reason why the approximated Hessian is rank deficient. We can remove the gauge freedom by fixing six parameters, e.g. the first pose. Thus, we would optimize over the poses T2, . . . , Tm and all points y1, . . . , yn while keeping T1 fixed which now defines the reference frame. 四件事： 1. 设置优化算法OptimizationAlgorithmLevenberg和线性求解器LinearSolverCSparse 2. 设置vertices(poses and landmarks) 和 edges (odometry constraints and landmark observations) 3. optimizer.initializeOptimization(); 4. optimizer.optimize(10); 部分关键数据和函数部分关键数据和函数

分享到：

赞收藏

资料库

视觉SLAM-g2o简介及使用方法.pdf

相关推荐

人工智能

热门标签

最新资料