第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
基于四元数的UKF多传感器卫星姿态确定研究.pdf
1. 引 言
1. UKF滤波算法
2.1 UKF算法
2.2 UKF算法预测方程[2]
2.3更新方程[2]
2. 相关数学模型
3.1卫星运动学及动力学方程
3.2矢量观测模型
3. UKF算法中四元数的处理
4. 仿真及结果分析
5. 结论
参考文献
基于四元数的UKF多传感器卫星姿态确定研究1
陈志明1，王惠南2，刘海颖3
http://www.paper.edu.cn
1 南京航空航天大学自动化学院，南京(210016)
2南京航空航天大学自动化学院，南京(210016)
3南京航空航天大学自动化学院，南京(210016)
E-mail:goki@163.com
摘 要： 本文针对采用磁强计及太阳敏感器的卫星姿态模型，应用UKF滤波算法对其进行
姿态确定。文中采用四元数描述姿态，并在算法中将其转换成旋转矢量来进行处理，同时还
设计了四元数求均值的叠代算法，解决了四元数在UKF算法中的处理问题。为了验证算法效
率，本文最后通过仿真将其与EKF算法进行对比。仿真结果表明EKF算法对初值依赖性较大，
而UKF算法不受初值影响且精度比EKF高，达到 3×10-3，具有快速性好、精度高和稳定性
强等优点。
关键词：姿态测量；四元数；UKF；矢量观测
中图分类号：V448.22
1. 引 言
多年来卡尔曼滤波[1]算法一直是姿态确定中必不可少的工具，是多传感器信息融合技术
的主要手段。在非线性系统中广泛采用的是广义卡尔曼滤波算法（EKF），它是通过对非线
性函数的Taylor展开式进行一阶线性截断，从而将非线性问题转化为线性，但在Taylor展开
式高阶项无法忽略时，线性化会产生较大的误差，另外EKF需要计算雅可比矩阵，计算量大。
UKF算法则使用采样方法近似非线性分布来解决非线性问题[2]。
UKF以UT变换为基础，采用卡尔曼线性滤波框架。计算精度至少达到 2 阶[3][4]，对于采
用特殊的采样策略，如高斯分布 4 阶采样和偏度采样等可达到更高阶精度[5]，它计算量与EKF
同阶，且不需计算雅可比矩阵。因此采用UKF将会达到比EKF更好的效果。
本文采用四元数来描述卫星姿态。与欧拉角相比，四元数表示方法不具奇异性，其计算
也比旋转矩阵效率更高[6]。
在刚体定点转动理论中有一个著名的欧拉定理：刚体绕固定点的任一位移，可由绕通过
此点的某一轴转过一个角度而得到。在单位时间间隔 tΔ 内假设刚体角速度为ω
，则该转动
轴的方向 及绕该轴转过的角度
φ分别为：
e
e ω
=
，
ω
t
φ ω=
Δ
相应四元数表示式为：
1 本课题得到高等学校博士学科点专项科研基金（20030287005）资助。
- 1 -
q
=
q
0
q
1
q
2
q
3
⎡
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎦
=
q
0
q
⎡
⎢
⎣
⎤
⎥
⎦
⎡
⎢
= ⎢
⎢
⎢
⎣
cos(
φ
)
2
φ
)
sin(
2
e
http://www.paper.edu.cn
⎤
⎥
⎥
⎥
⎥
⎦
(1)
满足约束条件
q
2
0
+
q
2
1
+
q
2
2
+
q
2
3
=
1
。
四元数本质上描述的是坐标转换，不仅反映相对参考坐标系的姿态，也可看作姿态机动
参数。如令姿态机动前的姿态参数为：
q
=
q q
0(
,
；机动后的姿态参数为：
)T
q
′
=
q q
0(
,
′
)T
′
；
姿态机动参数为：
,
。
q
q
(
Δ = Δ
0
Δ
q
)T
有姿态矩阵的乘积表达式：
− Δ
q q q q
Δ
0
q q
q q
T
Δ
0 0
q q
+ Δ + Δ ×
（本文中‘× ’均表示为卷积）
或：
⎡
′ = Δ ⊗ = ⎢
⎣
q
q
q
0
⎤
⎥
⎦
其中：
Δ = ⊗
q−
q q
1
′
q
q
0(
,
1
− =
−
q
2. UKF 滤波算法
)T
(2)
(3)
2.1 UKF 算法
针对如下非线性系统：
f x k u k v k
x k
(
[ ( ), ( ), ( )],
z k
( )
( )].
假设状态 x 为 n 维向量，均值为 x ，协方差为 ，v 为 维状态噪声，w 为 维观测
1)
+ =
h x k u k w k
[ ( ), ( ),
=
Px
(4)
(5)
q
m
v w
噪声， 与 线性无关。
1)
算法在每个
k k +
( ,
时间段内进行Sigma采样，得到Sigma点集
需对状态进行扩维处理[7]。针对式(4)(5)定义的系统，令：
{ }iχ 。由于具有噪声项，
x k
( )
a
=
x k
[ ( ) ,
T
v w
T
,
]
T T
由于本系统中噪声均为高斯白噪声，均值为零，因此有
Px
方差 扩维得：
Px k
( )
0
0
P k
( )
⎡
⎢
= ⎢
⎢
⎣
a
0
Q
0
0
0
R
⎤
⎥
⎥
⎥
⎦
x k
( )
a
=
x k
[ ( );0 ;0
q
1
×
]
m
1
×
。对协
本文采用对称采样方法，其 Sigma 点集生成算法如下：
χ
0
χ
i
χ
i
i
L
,
1,
,
=
i L
1,
= +
ˆ,
x
=
ˆ
x
= +
ˆ
x
= −
( (
( (
Px
Px
)
λ
)
λ
) ,
i
) ,
i
L
,2 .
L
L
+
+
- 2 -
(6)
= + + 为 的维数，令
aP
其中 L n q m
n q+
维组成的列向量，
w
iχ 为 a
iχ 的前
x
iχ 为 a
iχ 的前 维组成的列向量，
n
v
1n +
+ + 维组成的列向量。其预测
iχ 为 a
iχ 的
n q+ + 维到 n q m
1
维到
http://www.paper.edu.cn
方程及更新方程如下。
2.2 UKF算法预测方程[2]
|
1|
+
k
k
(
)
(
[
x
χ
i
x
χ
i
(
Px k
+
1|
k
Z k
(
i
+
1|
k
)
=
2
f
L
∑
i
=
0
2
L
)
=
∑
i
0
=
h
[
x
χ
=
i
L
2
∑
i
=
0
2
L
∑
i
=
0
L
2
∑
i
=
0
(
P k
xv
+
1|
k
)
=
2.3 更新方程[2]
ˆ(
x k
+
1|
k
)
=
W
i
m x
χ
i
(
k
+
1|
k
)
,
k k u k
), ( ),
v
iχ
k
( )]
,
W
i
c
(
x
χ
i
(
k
+
1|
k
)
−
ˆ
x k
(
+
1|
k
)
)(
x
χ
i
(
k
+
1|
k
)
−
ˆ
x k
(
+
1|
k
)
T
)
,
(
k
+
1|
k u k
), ( ),
w
χ
i
(
k
+
1)],
ˆ(
z k
+
1|
k
)
=
m
W Z k
(
i
i
+
1|
k
),
P k
(
vv
+
1|
k
)
=
c
W Z k
(
(
i
i
+
1|
k
)
−
ˆ
z k
(
+
1|
k
)
)(
Z k
(
i
+
1|
k
)
−
ˆ
z k
(
+
1|
k
)
T
)
,
c
W
i
(
x
χ
i
(
k
+
1|
k
)
−
ˆ
x k
(
+
1|
k
)
)(
Z k
(
i
+
1|
k
)
−
ˆ
z k
(
+
1|
k
)
T
)
,
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
W k
(
ˆ
x k
(
+
Px k
(
1)
+ =
k
1|
1|
+
P k
(
+
xv
ˆ
x k
1)
(
+ =
k
1)
+ =
1k +
k
k P k
1|
),
1|
(
)
1
−
+
vv
k W K
z k
1)( (
)
(
1|
+
+
+
k W k
Px k
1|
(
)
(
−
+
+
)),
ˆ
k
z k
1|
1)
(
+
+ −
k W k
P k
1)
+ ,
(
1|
)
1)
(
+
vv
Px k
+ 和协方差 (
k+
1)
1|
T
+
于是得到
时刻的状态估计值
ˆ(
x k
1|
k
1
)
+ 。方程中涉及到以
下参量：
c
m
iW
iW 为均值加权所用权值， 为协方差加权所用权值。其值分别为：
W
L
)
/(
m
=
+
λ λ
0
L
W
(1
)
/(
c
λ λ
+
+ −
=
0
L
W W
1/[2(
m
c
+
=
=
i
如果采用的为非加权运算，则其值均为1/(2
)
λ α κ
)
α β
+
=
i
1,
)],
λ
L + [8]。
L
,2 .
2(
1)
+
2
i
n
=
− n 为UKF比例系数，α决定了Sigma点在状态均值 x 周围的分布，该值
1α− ≤ ≤ 。β为一个与状态先验分布信息有关
的选取目前没有特定的要求，一般取值： 410
2β= 是最优的[9]。而对
的参数，为非负的权系数，当传感器以及系统噪声为高斯分布时，
于非高斯分布的情况，需要通过对具体的仿真实验来选取更好的β值。对于 的取值，当
状态量为单变量时，选择
，状态变量为多变量时，选取
κ= − 。
2κ=
3 n
κ
(17)
- 3 -
3. 相关数学模型
3.1 卫星运动学及动力学方程
http://www.paper.edu.cn
本滤波算法的状态量选取四元数及角速度：
x
由四元数表述的卫星运动学方程为[10]：
q q q q ω ω ω
z
0
]T
=
[
1
2
3
x
y
(18)
q
1 (
qω= Ω
)
2
Ω
(
)
ω
=
y
x
0
−
ω ω ω
−
−
⎡
z
⎢
0
−
ω ω
ω
⎢
x
z
y
0
⎢
ω
ω ω
−
x
z
⎢
0
ω ω ω
⎢
⎣
x
y
y
z
⎤
⎥
⎥
⎥
⎥
⎥
⎦
−
其动力学方程为[10]：
I
)
ω ω ω
式中 M 为施加在卫星上总的力矩，也即控制量u 。两方程中ω均为星体坐标系下的角
+ ×
(19)
M
=
I
(
速度。
I 为卫星惯量阵，在本研究中所用卫星模型惯量阵为：
I
1.1
⎡
⎢
0
= ⎢
0
⎢
⎣
0
1.2
0
0
0
1.0
⎤
⎥
⎥
⎥
⎦
由于四元数不能直接叠加噪声（这一点在下一节详细介绍），式(4)表述的状态方程在
未叠加噪声时应为：
1 (
Ω
2
u
)]
[
ω ω
− ×
q
⎡ ⎤
⎢ ⎥
ω
⎣ ⎦
⎡
⎢=
⎢
⎣
)
ω
q
1
−
I
I
(
⎤
⎥
⎥
⎦
离散形式为：
q k
(
⎡
⎢
k
(
ω
⎣
+
+
1)
1)
⎤
⎥
⎦
⎡
⎢=
⎢
⎣
1
−
I
1
2
u k
[ ( )
−
Ω
(
ω
k
( ))
t q k
( )
Δ +
ω
k
( )
×
(
I
ω
k
( ))]
t
Δ +
⎤
⎥
⎥
⎦
ω
k
( )
(20)
(21)
3.2 矢量观测模型
在卫星轨道坐标系下，地球磁场强度及太阳方向都是可以通过该轨道信息及星历解算出
来的。它们都是三维的向量。卫星轨道坐标系下磁场强度及太阳方向的参考量记为 OB 与
OS
，地磁场数据还需参考国际地磁参考场IGRF（International Geomagnetic Reference Field）
BB 与 ，它们
。以四元数表述的当前姿态
获得。而卫星磁力计与太阳敏感器得到的测量值为星体坐标下的值，记为
之间可以通过姿态转换阵
BS
；
O
O
B
OR 转换： B
B
B
=
R B
B
O
S
=
R S
B
O
- 4 -
http://www.paper.edu.cn
(22)
(23)
下的轨道与星体坐标转换阵如下[10]：
+
−
−
q
q
2
2
−
2
1
q q
2(
1 2
q q
2(
1 3
q
2
−
+
3
q q
−
0 3
q q
+
0 2
q q
1 2
q
2
+
2
q q
2 3
2(
q
2
1
2(
q
2
0
)
)
R
B
O
=
−
⎡
⎢
⎢
⎢
⎣
因此式(5)表述的观测方程应为：
q q
)
0 3
q
q
2
2
+
3
0
q q
)
0 1
2(
2(
q
2
1
q q
1 3
q q
2 3
q
2
−
2
−
+
+
q q
)
0 2
q q
)
0 1
q
q
2
2
+
0
3
−
⎤
⎥
⎥
⎥
⎦
O
O
=
ˆ ( )
R k B
B
O
ˆ ( )
R k S
B
O
k
⎡
⎢
⎢
⎣
ˆ ( )
OR k
B
z k
( )
其中
+
w k
( )
⎤
⎥
⎥
⎦
由 时刻四元数姿态估计值得到。
由此得到了卫星状态方程及观测方程。
4. UKF 算法中四元数的处理
由于四元数并非普通矢量，不能按照上述预测及更新方程直接运算。对于公式(7)表述
的状态函数：控制量
作用产生新的角速度同时产生新的四元数并叠加噪声项。考虑到
刚体转动为三轴方向转动，其姿态误差也应为三维，加上角速度误差，状态量误差应为 6
( )u k
=
v vω
(
)T
,
q
。
维：
v k
( )
vω
可以直接相加，叠加噪声后的角速度
ω ω=
+
vω
，而 qv
则可以当作旋转矢量，按下
述公式转换成机动姿态 。
qΔ
qvφ =
v
e
v
=
，
v
q
v
q
(24)
T
)
φ
v
2
eφ
),
v
v
2
sin(
cos(
⎡
q
Δ = ⎢⎣
⎤
⎥
⎦
叠加噪声后的姿态四元数
同样对于公式(9)，角速度部分可以按公式直接求差，四元数部分按照式(3)计算差量，
维的。
再将差量 按照上述方法进行反运算转换成旋转矢量。这样生成的协方差阵为
q= Δ ⊗
(25)
。
q
q
6 6×
qΔ
同样的公式
(13)(15)都应作相应处理。
对于公式(8)表述的是一个求加权均值的过程。状态量的角速度部分可以直接按公式运
算，四元数部分可以采用叠代算法求出。文献[8]给出了一个四元数求均值的叠代算法，本文
采用的则是四元数加权求均值的算法，基本思路如下：
= ，先将其转换为旋转矢量 { }iv
1,
n
,
，并乘上相应权值得
对于一组四元数 { },
iW v
{
}m
iq
，再转换成新的四元数集{ }iq′ 。
i
i
任意选取一个四元数 作为其均值的估计，分别计算 与
tq
iq′ 间的差值
e
i
′= ⊗
q
i
1
q−
t
，
tq
计算 的均值
ie
e
1 n
= ∑ ，对 e 标准化 (
n =
i
1
e
i
e
′ =
e
e
- 5 -
) ，并计算新的均值估计 t
q
′
′= ⊗ 。这样
e
q
t
重复运算直到 e′ 满足特定条件，一般来讲当 e′ 近似于[
{ }iq 的均值 。
与 基本无旋转变换。这样便得到了
tq
tq
1 0 0 0]T
http://www.paper.edu.cn
就可以停止叠代，它表示
tq ′
基于以上理论，便可以在 UKF 算法中引入四元数。
5. 仿真及结果分析
为[
为了验证算法效果，本文采用某小卫星模型，其轨道高度为700km，初始姿态的欧拉角
20 30 40 ]
rad s
/
本文采用四元数估计值与真实值间的均方差EMS作为分析的依据。
，初始星体坐标系下角速度为[
0.005 0.003 0.001]
，仿真步长选取1s。
EMS
=
n
−∑
ˆ(
x
i
i
=
0
x
i
2
)
为了说明UKF的优越性，本文引入EKF算法滤波结果作为比较。
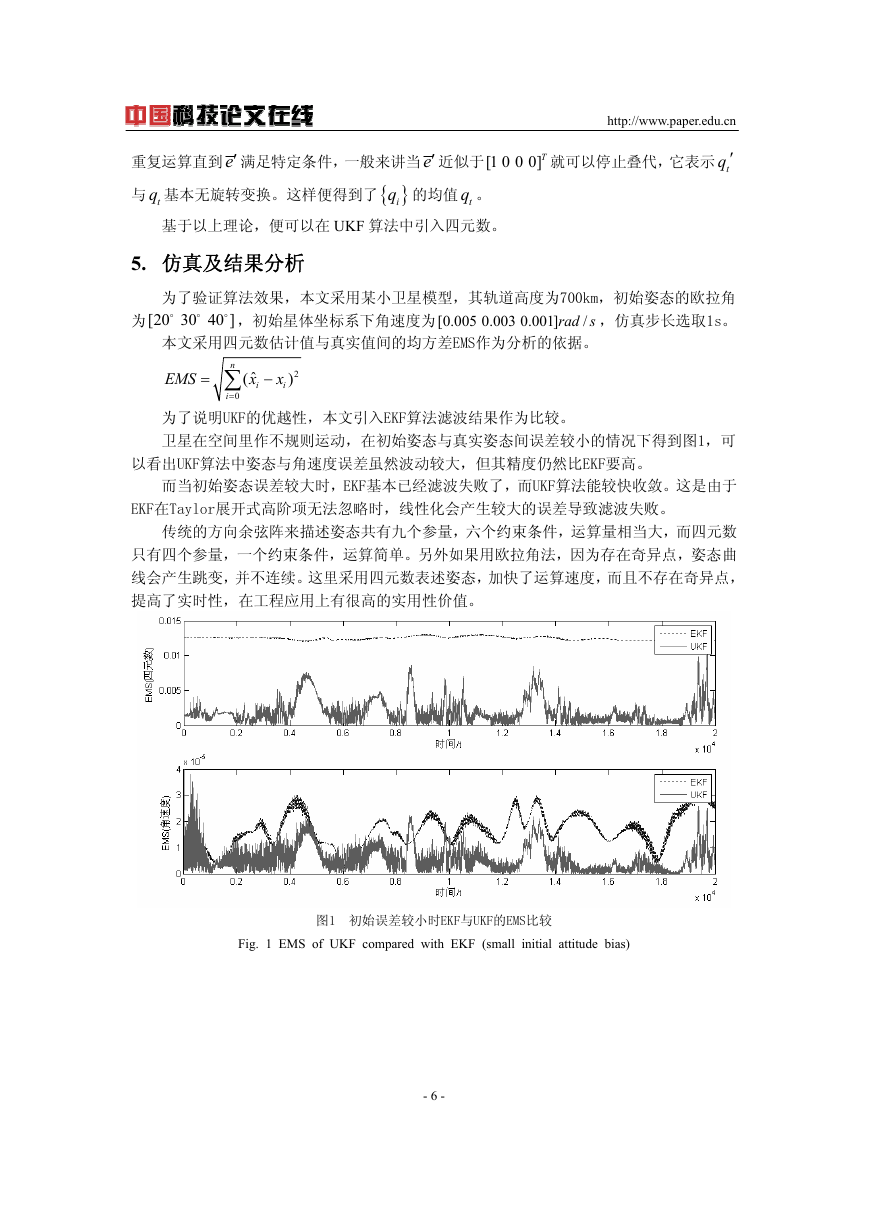
卫星在空间里作不规则运动，在初始姿态与真实姿态间误差较小的情况下得到图1，可
以看出UKF算法中姿态与角速度误差虽然波动较大，但其精度仍然比EKF要高。
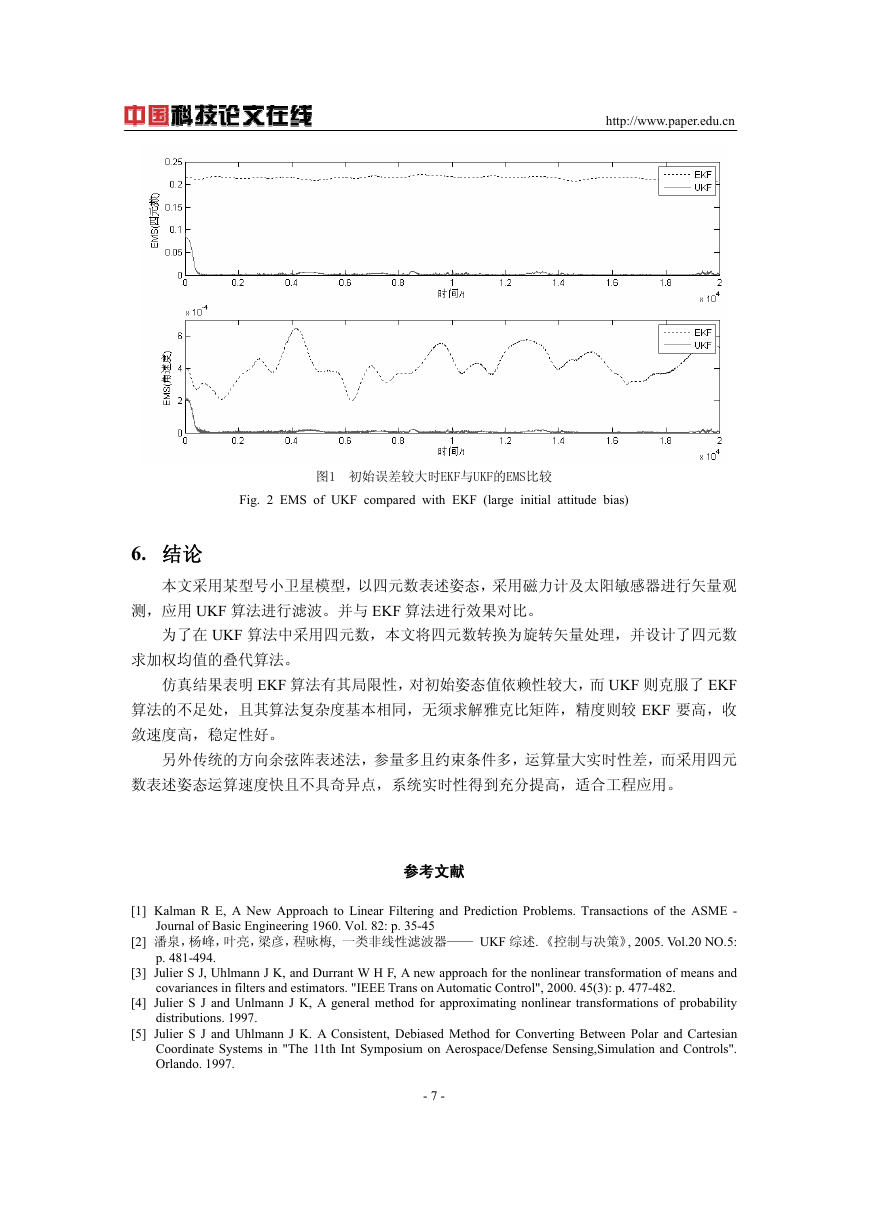
而当初始姿态误差较大时，EKF基本已经滤波失败了，而UKF算法能较快收敛。这是由于
EKF在Taylor展开式高阶项无法忽略时，线性化会产生较大的误差导致滤波失败。
传统的方向余弦阵来描述姿态共有九个参量，六个约束条件，运算量相当大，而四元数
只有四个参量，一个约束条件，运算简单。另外如果用欧拉角法，因为存在奇异点，姿态曲
线会产生跳变，并不连续。这里采用四元数表述姿态，加快了运算速度，而且不存在奇异点，
提高了实时性，在工程应用上有很高的实用性价值。
图1 初始误差较小时EKF与UKF的EMS比较
Fig. 1 EMS of UKF compared with EKF (small initial attitude bias)
- 6 -
http://www.paper.edu.cn
图1 初始误差较大时EKF与UKF的EMS比较
Fig. 2 EMS of UKF compared with EKF (large initial attitude bias)
6. 结论
本文采用某型号小卫星模型，以四元数表述姿态，采用磁力计及太阳敏感器进行矢量观
测，应用 UKF 算法进行滤波。并与 EKF 算法进行效果对比。
为了在 UKF 算法中采用四元数，本文将四元数转换为旋转矢量处理，并设计了四元数
求加权均值的叠代算法。
仿真结果表明 EKF 算法有其局限性，对初始姿态值依赖性较大，而 UKF 则克服了 EKF
算法的不足处，且其算法复杂度基本相同，无须求解雅克比矩阵，精度则较 EKF 要高，收
敛速度高，稳定性好。
另外传统的方向余弦阵表述法，参量多且约束条件多，运算量大实时性差，而采用四元
数表述姿态运算速度快且不具奇异点，系统实时性得到充分提高，适合工程应用。
参考文献
[1] Kalman R E, A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME -
Journal of Basic Engineering 1960. Vol. 82: p. 35-45
[2] 潘泉，杨峰，叶亮，梁彦，程咏梅, 一类非线性滤波器—— UKF 综述. 《控制与决策》, 2005. Vol.20 NO.5:
p. 481-494.
distributions. 1997.
[3] Julier S J, Uhlmann J K, and Durrant W H F, A new approach for the nonlinear transformation of means and
covariances in filters and estimators. "IEEE Trans on Automatic Control", 2000. 45(3): p. 477-482.
[4] Julier S J and Unlmann J K, A general method for approximating nonlinear transformations of probability
[5] Julier S J and Uhlmann J K. A Consistent, Debiased Method for Converting Between Polar and Cartesian
Coordinate Systems in "The 11th Int Symposium on Aerospace/Defense Sensing,Simulation and Controls".
Orlando. 1997.
- 7 -
[6] Dam E., Koch M., and Lillholm M., Quaternions, Interpolation and Animation. Technical Report
http://www.paper.edu.cn
DIKU-TR-98/5,Department of Computer Science, 1998.
[7] Eric A Wan and Rudolph van der Merwe, The Unscented Kalman Filter 2001.
[8] Edgar Kraft. A Quaternion-based Unscented Kalman Filter for Orientation Tracking. in "Proceedings of the
6th International Conference on Infornation Fusion". Cairns, Australia. 2003.
[9] Wan E A and Merwe R. The unscented Kalman filter for nonlinear estimation[C]. in "Proc of IEEE
Symposium 2000 on Adaptive Systems for Signal Processing,Communicat ions and Control". Canada. 2000.
[10] 章仁为, 《卫星姿态动力学与控制》, 北京: 北京航空航天大学出版社. 1998.
Research on Satellite Attitude Estimation with multisensor
Based on Quaternion Using Unscented Kalman Filtering
College of Automation Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing,
CHEN Zhi-ming, WANG Hui-nan, LIU Hai-ying
210016, China
Abstract
In present paper, a satellite model with magnetometers and sun sensors was referred. Attitude
based on quaternion was estimated by UKF (Unscented Kalman Filtering) arithmetic. Quaternion was
transferred into rotation vector in order to match the arithmetic, besides an iterated algorithm was
designed to calculate the mean quaternion. In the end of this paper simulation was carried out to test
the efficiency of UKF compared with EKF. The result proved UKF arithmetic was unaffected by
initial data and more effective with high preci-sion and stabilization.
Keywords: Attitude estimation; Quaternion; UKF; Vector observation
作者简介：陈志明（1982-） 男，博士，研究方向：卫星姿态测量与控制，GPS 导航
- 8 -
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
