第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
磁化黑洞中光子的偏转角和非线性电动力学的影响.pdf
Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics
Abstract
1 Introduction
2 Weak gravitational lensing and magnetized black hole
3 Deflection angle of photon and Gauss–Bonnet theorem
4 Graphical analysis
4.1 Deflection angle with Impact parameter b
5 Conclusion
Acknowledgements
References
Eur. Phys. J. C (2019) 79:694
https://doi.org/10.1140/epjc/s10052-019-7208-3
Regular Article - Theoretical Physics
Deflection angle of photon from magnetized black hole and effect
of nonlinear electrodynamics
Wajiha Javed1,a, Jameela Abbas1,b, Ali Övgün2,3,c
1 Department of Mathematics, University of Education, Township, Lahore 54590, Pakistan
2 Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla, 4950 Valparaiso, Chile
3 Physics Department, Faculty of Arts and Sciences, Eastern Mediterranean University, North Cyprus, via Mersin 10, Famagusta, Turkey
Received: 17 April 2019 / Accepted: 7 August 2019 / Published online: 19 August 2019
© The Author(s) 2019
Abstract
In this paper, we analyze deflection angle of pho-
ton from magnetized black hole within non-linear electrody-
namics with parameter β. In doing so, we find the correspond-
ing optical spacetime metric and then we calculate the Gaus-
sian optical curvature. Using the Gauss–Bonnet theorem, we
obtain the deflection angle of photon from magnetized black
hole in weak field limits and show the effect of non-linear
electrodynamics on weak gravitational lensing. We also ana-
lyzed that our results reduces into Maxwell’s electrodynam-
ics and Reissner–Nordström (RN) solution with the reduc-
tion of parameters. Moreover, we also investigate the graph-
ical behavior of deflection angle w.r.t correction parameter,
black hole charge and impact parameter.
1 Introduction
In 1916, Einstein cleverly predicted the existence of gravi-
tational waves and gravitational lensing as part of the the-
ory of general relativity [1]. In 2015, the gravitational waves
were detected by LIGO [2], which shows that the theoretical
predictions are well fitted with experimental observations.
Hence, this new detection of gravitational waves marks not
only a culmination of a decades-long search, but also the
beginning of a new way to look at the universe. After detec-
tion of gravitational waves by LIGO, there is renewed interest
in the topic of gravitational lensing [3]. Gravitational lensing
first proposed by Soldner in 1801 in context of Newtonian
theory [4]. Many useful results for cosmology have come out
of using this property of matter and light. Then using data
taken during a solar eclipse in 1919, Eddington measured a
a e-mails: wajiha.javed@ue.edu.pk; wajihajaved84@yahoo.com
b e-mail: jameelaabbas30@gmail.com
c e-mail: ali.ovgun@pucv.cl
URL: https://www.aovgun.com
value close to that of the GR prediction [5,6]. Then gravita-
tional lensing has been worked in various space-times using
different methods [7–15].
Moreover, over the years, there have been many studies
linking gravitational lensing with the Gauss–Bonnet theorem
(GBT) after Gibbons and Werner (GW) elegantly showed that
the possible way of calculation the deflection angle using the
GBT for asymptotically flat static black holes [16]:
α = −
Kdσ,
S∞
Here K and dσ are the Gaussian curvature and surface ele-
ment of optical metric.
Afterwards, Werner extended this method for stationary
black holes [17]. Next, Ishihara et al. [18] showed that it is
possible to find deflection angle for the finite-distances (large
impact parameter) because the GW only found the deflec-
tion angle using the optical Fermat geometry of the black
hole’s spacetime in weak field limits and for the observers
at asymptotically flat region. Recently, Crisnejo and Gallo
have studied the deflection of light in a plasma medium [19].
Since then, there is a continuously growing interest to the
weak gravitational lensing via the method of GW and GBT
of black holes, wormholes or cosmic strings [20–40].
The main aim of this paper is to investigate the effect of
the nonlinear electrodynamics (magnetized) charge on the
deflection angle where we use the GBT in which the deflec-
tion of light become a global effect [41]. Because we only
focus the nonsingular region outside of a photon rays.
Gravitational singularities are mainly considered within
general relativity, where density apparently becomes infinite
at the center of a black hole, and within astrophysics and
cosmology as the earliest state of the universe during the Big
Bang. In general theory of gravity, spacetime singularities
raise a number of problems, both mathematical and physical
[42–50]. Using the nonlinear electrodynamics it is possible
123
694 Page 2 of 7
Eur. Phys. J. C (2019) 79 :694
to remove these singularities by constructing a regular black
hole solution [51–55]. Recently, Kruglov has proposed a new
model of nonlinear electrodynamics with two parameters β
and γ where the the specific range of magnetic field, the
causality and unitary principles are satisfied [41]. Moreover,
it is shown that there is no singularity of the electric field
strength at the origin for the point-like particles and it has a
magnetic charge. Moreover, AN Aliev et al. showed the effect
of the magnetic field on the black hole space time [56–60].
This paper is organized as follows. In Sect. 2, we briefly
review the solution of magnetized black hole and then we
calculate its optical geometry and the optical curvature. In
Sect. 3, deflection angle of photon using the GBT is studied
in the case of magnetized black hole. In Sect. 4, we analysis
the deflection angle in details using the graphical analysis.
And we concludes in Sect. 4 with a discussion regarding the
results obtained from the present work.
2 Weak gravitational lensing and magnetized black hole
,
1
d4x
√−g
2k2 R + L
The action for the Einstein with a nonlinear electrodynamics
(NLED) is given as [41]
J =
where k2 = 8π G ≡ M
−2
pl , M pl is for reduced planck mass,
G is Newtonian constant and R is Ricci scalar. From above
equation we derived the Einstein equations as
Rab − 1
2
gab R = −k2Tab.
(1)
(2)
Now, we derive the equation of motion for electromagnetic
fields by varying (1)
√−g(F abLF + ¯F abLG )) = 0.
∂a(
(3)
Now, we analyze the static magnetic black hole solution by
using the Einstein field equation and equation of motion for
electromagnetic field with above equations. In the case of
pure magnetic field, Bronnikov showed [51] that when spher-
ical symmetry holds, the invariant is F = q2/(2r 2), where
q is a magnetic charge. In this case, the line element of the
static and spherical symmetric space-time is
ds2 = − f (r )dt 2 + 1
f (r )
dr 2 + r 2(dθ 2 + sin2 θdϕ2),
(4)
by assuming both the source and observer are in the equatorial
plane likewise trajectory of the null photon is also on the same
plane with(θ = π
), we obtain the optical metric as follows
ds2 = − f (r )dt 2 + 1
f (r )
dr 2 + r 2dϕ2.
(5)
2
123
For moving photon in the equatorial plane and null geodesics,
ds2 = 0, we get
dt 2 = 1
dϕ2.
(6)
f (r )2 dr 2 + r 2
f (r )
.
(7)
f (r )
, ζ = r√
Subsequently, we make the transformation into new coordi-
nate u, the metric function ζ (u) as
du = dr
f (r )
Then the optical metric tensor ¯gab is as follows
dt 2 = ¯gabdx adx b = du2 + ζ 2dϕ2.
(8)
It is to be noted that (a, b) → (r, ϕ) and determinant is
det ¯gab = r 2
f (r )3 . Now using Eq.(8), the non-zero Christopher
r ϕ =
= − f
symbols are r
rr
−r f
ϕr . Hence, we can find the Gaussian optical
curvature K [16] as follows
K = − Rr ϕr ϕ
d2ζ
det ¯gr ϕ
du2
ϕϕ = r (r f
(r )+2 f (r )
2r f (r )
(r )
f (r ) , r
(r )−2 f (r ))
= − 1
= ϕ
, ϕ
(9)
ζ
2
.
Now, we rewrite Gaussian optical curvature in terms of
Schwarzschild radial coordinate r [61]:
K = − 1
2 d2ζ
+
.
(10)
dr
du
d
dr
dr
du
dζ
dr
ζ
dr
du
dr 2
By applying Eq. (10) into our metric (6) we obtain the Gaus-
sian optical curvature of photon from magnetized black hole,
which yields that
K = −
(r )2 − 2 f (r ) f
(r ))
√
r ( f
√
,
(11)
f (r )
r
4
f (r )
where the function f (r ) is [41]
f (r ) = 1 − 2Gm
r
+ Gq2
r 2
− βGq4
5r 6
+ O(r
−10).
(12)
After substituting the value of f (r ), we get the value of opti-
cal curvature up to leading orders
K − 2Gm
− 21βGq4
r 3
+ 3Gq2
r 4
G2, m2
+ O
(13)
5r 8
.
3 Deflection angle of photon and Gauss–Bonnet
theorem
Now, we use the Gauss–Bonnet theorem to derive the deflec-
tion angle of photon for magnetized black hole. We apply the
Gauss–Bonnet theorem to the region MR, stated as [16]
kdt +
θ j = 2πX (MR).
(14)
∂MR
Kd S +
MR
j
Eur. Phys. J. C (2019) 79 :694
Page 3 of 7 694
MR
∂MR
Here K is for Gaussian curvature and the geodesic curvature
is k, given as k = ¯g(∇˙α ˙α, ¨α) in such a way that ¯g(˙α, ˙α) = 1,
where θ j is the representation for exterior angle at the jth
vertex and ¨α is unit acceleration vector. The jump angles
become π/2 as R → ∞ and we get θO + θS → π. The
Euler characteristic is X (MR) = 1, as MR is non singular.
Therefore we get
Kd S +
kdt + θ j = 2πX (MR).
The radial component of the geodesic curvature is given by
(15)
where θ j = π shows the total jump angle and α¯g is a
geodesic; since the Euler characteristic number X is 1. As
˙DR |.
R → ∞ the remaining part yield that k(DR) =| ∇ ˙DR
(∇ ˙DR
(16)
At very large R, DR := r (ϕ) = R = const. Therefore, the
first term of equation (17) vanish and ( ˙Dϕ
ζ . Recalling
ϕϕ = r (r f
˙Dr
(∇ ˙Dr
(r )−2 f (r ))
)r → −1
˙DR)r = ˙Dϕ
ϕϕ( ˙Dϕ
)2 = 1
+ r
, we get
˙Dr
(17)
)2.
r
∂ϕ
R
R
2
R
R
R
R
,
R
and it shows that the geodesic curvature is independent of
topological defects, k(DR) → R
−1. But from the optical
metric (8), we can say that dt = Rdϕ. Therefore we find
that
k(DR)dt = 1
R
Rdϕ.
(18)
Taking into account the above results, we obtain
Kd S
kdt = R→∞
Kd S +
MR
∂MR
π+
S∞
+
dϕ.
(19)
0
In the weak deflection limit, by assuming that at the zeroth
order the light ray is given by r (t ) = b/sin ϕ. Thus by using
(14) and (20), the deflection angle becomes [16]
= −
det ¯gdudϕ,
∞
π
(20)
K
0
b/ sin ϕ
where,
det ¯gdu = rdr
1 − 6mG
r
+ 3Gq2
r 2
− 3q4Gβ
5r 6
.
(21)
After substituting the leading order term of Gaussian curva-
ture (14) into equation(21), the deflection angle up to second
order term is calculated as follows:
+ 7Gπβq4
32b6
− 3π Gq2
4b2
4mG
(22)
≈
b
.
4 Graphical analysis
This section is devoted to discuss the graphically behavior
of deflection angle . We also demonstrate the physical sig-
nificance of these graphs to analyze the impact of correction
parameter β, BH charge q, and impact parameter b on deflec-
tion angle by examining the stability and instability of BH.
4.1 Deflection angle with Impact parameter b
This subsection gives the analysis of deflection angle with
impact parameter b for different values of correction param-
eter β and BH charge q in geometrized unit 8π G = 1.
• Figure 1 shows the behavior of with b for varying q
and for fixed value for correction parameter.
1. In figure (i), we examined that the deflection angle
exponentially decreases for small variation of q.
2. In figure (ii), we analyzed that the deflection angle
gradually decreasing and then eventually goes to
infinity for large variation of q which is the unsta-
ble state of magnetized BH.
Therefore, we conclude that for small values of q the
magnetized BH is stable but as q increases it shows
the unstable behavior of magnetized BH.
In Fig. 2, indicates the behavior of deflection angle with
impact parameter by varying correction parameter β.
1. In figure (i), we noticed that the deflection angle
decreasing constantly for small values of β but in
2. In figure (ii), as β increases the deflection angle grad-
ually decreasing and then goes to infinity.
• Figure 3 shows the behavior of with correction param-
eter β.
1. In figure (i), shows the behavior of with β, for
varying b and fixed q. This shows that when b < 0
it gives the uniform negative behavior but for b > 0
it behave as a positive slope. We also conclude that
for 4 ≤ b < 15 the behavior is negative slope but for
b ≥ 15 it gives positive slope.
2. In figure (ii), indicate the behavior of with β, for
the variation of q and fixed b. We examined that the
deflection angle is positively increasing with increase
of q but for 5 ≤ q ≤ 10 the behavior is negative and
then it becomes positive.
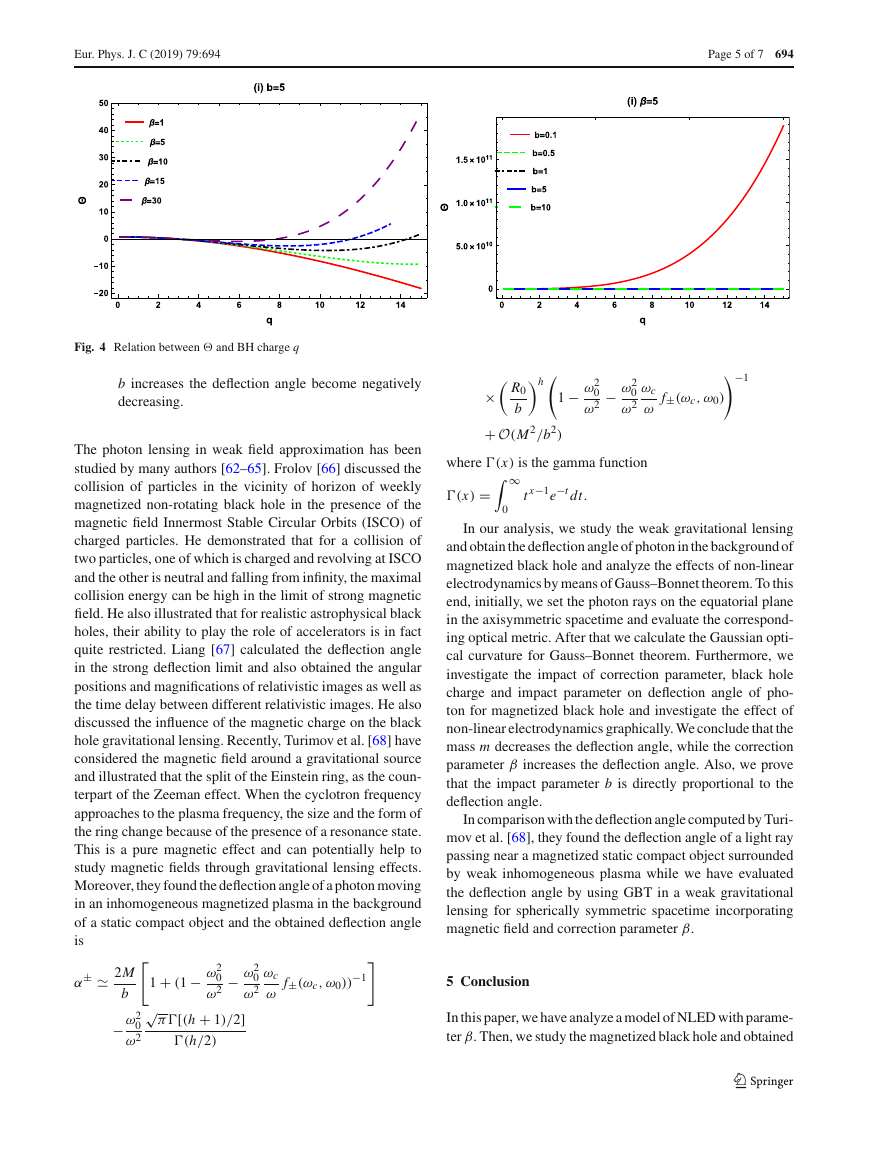
In Figure 4, represent the behavior of deflection angle
with BH charge q.
1. In figure (i), represents the behavior of with q, by
varying β and fixed b. We analyzed that the deflection
123
694 Page 4 of 7
Eur. Phys. J. C (2019) 79 :694
Fig. 1 Relation between and impact parameter b
=
=
=
=
=
Fig. 2 Relation between and impact parameter b
Fig. 3 Relation between and correction parameter β
angle initially decreases but as β increases the deflec-
tion angle firstly decreases and then increases. We
also observe that for β > 20 the behavior is increas-
ing.
2. In figure (ii), shows the behavior of with q, by
varying b and fixed β. We observed that the deflec-
tion angle is increasing for smaller values of b but as
123
Eur. Phys. J. C (2019) 79 :694
Page 5 of 7 694
Fig. 4 Relation between and BH charge q
b increases the deflection angle become negatively
decreasing.
The photon lensing in weak field approximation has been
studied by many authors [62–65]. Frolov [66] discussed the
collision of particles in the vicinity of horizon of weekly
magnetized non-rotating black hole in the presence of the
magnetic field Innermost Stable Circular Orbits (ISCO) of
charged particles. He demonstrated that for a collision of
two particles, one of which is charged and revolving at ISCO
and the other is neutral and falling from infinity, the maximal
collision energy can be high in the limit of strong magnetic
field. He also illustrated that for realistic astrophysical black
holes, their ability to play the role of accelerators is in fact
quite restricted. Liang [67] calculated the deflection angle
in the strong deflection limit and also obtained the angular
positions and magnifications of relativistic images as well as
the time delay between different relativistic images. He also
discussed the influence of the magnetic charge on the black
hole gravitational lensing. Recently, Turimov et al. [68] have
considered the magnetic field around a gravitational source
and illustrated that the split of the Einstein ring, as the coun-
terpart of the Zeeman effect. When the cyclotron frequency
approaches to the plasma frequency, the size and the form of
the ring change because of the presence of a resonance state.
This is a pure magnetic effect and can potentially help to
study magnetic fields through gravitational lensing effects.
Moreover, they found the deflection angle of a photon moving
in an inhomogeneous magnetized plasma in the background
of a static compact object and the obtained deflection angle
is
α± 2M
b
− ω2
0
ω2
− ω2
1 + (1 − ω2
0
ω2
√
π [(h + 1)/2]
f±(ωc, ω0))−1
ωc
ω
0
ω2
(h/2)
h
1 − ω2
0
ω2
−1
− ω2
0
ω2
ωc
ω
f±(ωc, ω0)
R0
b
×
+O(M 2/b2)
∞
where (x) is the gamma function
(x) =
t x−1e
−t dt.
0
In our analysis, we study the weak gravitational lensing
and obtain the deflection angle of photon in the background of
magnetized black hole and analyze the effects of non-linear
electrodynamics by means of Gauss–Bonnet theorem. To this
end, initially, we set the photon rays on the equatorial plane
in the axisymmetric spacetime and evaluate the correspond-
ing optical metric. After that we calculate the Gaussian opti-
cal curvature for Gauss–Bonnet theorem. Furthermore, we
investigate the impact of correction parameter, black hole
charge and impact parameter on deflection angle of pho-
ton for magnetized black hole and investigate the effect of
non-linear electrodynamics graphically. We conclude that the
mass m decreases the deflection angle, while the correction
parameter β increases the deflection angle. Also, we prove
that the impact parameter b is directly proportional to the
deflection angle.
In comparison with the deflection angle computed by Turi-
mov et al. [68], they found the deflection angle of a light ray
passing near a magnetized static compact object surrounded
by weak inhomogeneous plasma while we have evaluated
the deflection angle by using GBT in a weak gravitational
lensing for spherically symmetric spacetime incorporating
magnetic field and correction parameter β.
5 Conclusion
In this paper, we have analyze a model of NLED with parame-
ter β. Then, we study the magnetized black hole and obtained
123
694 Page 6 of 7
Eur. Phys. J. C (2019) 79 :694
the regular black hole solution. After that we calculate the
optical Gaussian curvature for magnetized black hole. Then
by using Gauss–Bonnet theorem, we calculate the weak grav-
itational lensing. We obtain the following angle of deflection
for magnetized black hole
− 3π Gq2
4b2
+ 7Gπβq4
32b6
.
4mG
b
≈
(23)
We conclude that for f (r ) if r → ∞ the space-time becomes
flat, if β = 0 the NLED model converted into Maxwell’s
electrodynamics and the solution becomes RN solution. We
have analyzed the behavior of deflection angle w.r.t impact
parameter b, correction parameter β and BH charge q.
The results obtained from the analysis of deflection angle
given in the paper are summarized as follows:
Deflection angle with respect to impact parameter:
• In our analysis we have to discussed the behavior of
deflection angle, for this we choose different values of
BH charge q and fixed correction parameter. For smaller
values, the deflection angle gradually decreasing but for
large values of q the deflection angle gradually decreases
and then goes to infinity.
• While for fixed q and different values of β, the deflec-
tion angle constantly decreases for small range of β and
gradually decreases for greater values.
• Thus, we conclude that for smaller values, BH indicates
the stability and for large values shows the instability of
BH.
Deflection angle with respect to correction parameter:
• The behavior of w.r.t β, for fixed q and varying b,
positive behavior can be observed only for b > 0 except
4 ≤ b < 15.
• The behavior of w.r.t β, for fixed b and varying q,
the behavior is positively increasing for q > 0 except
5 ≤ q ≤ 10.
Deflection angle with respect to black hole charge:
• The behavior of w.r.t q, for fixed b and varying β, the
deflection angle initially decreases but with the increase
of β, the deflection angle firstly decreases and then
increases. For β > 20 the deflection angle positively
increases.
• The behavior of w.r.t q, for fixed β and choose different
values of b, the deflection angle positively increases for
small b and negatively decreases for greater b.
Acknowledgements This work was supported by Comisión Nacional
de Ciencias y Tecnología of Chile through FONDECYT Grant N o
3170035 (A. Ö.).
123
Data Availability Statement This manuscript has no associated data or
the data will not be deposited. [Authors’ Comment: This is a theoretical
study and no experimental data has been listed.]
Open Access This article is distributed under the terms of the Creative
Commons Attribution 4.0 International License (http://creativecomm
ons.org/licenses/by/4.0/), which permits unrestricted use, distribution,
and reproduction in any medium, provided you give appropriate credit
to the original author(s) and the source, provide a link to the Creative
Commons license, and indicate if changes were made.
Funded by SCOAP3.
References
1. A. Einstein, Lens-like action of a star by the deviation of light in
the gravitational field. Science 84, 506 (1936)
2. B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations],
Observation of gravitational waves from a binary black hole merger.
Phys. Rev. Lett. 116(6), 061102 (2016)
3. S.S. Li, S. Mao, Y. Zhao, Y. Lu, Gravitational lensing of gravita-
tional waves: a statistical perspective. Mon. Not. R. Astron. Soc.
476(2), 2220 (2018)
4. J. Soldner, Ueber die Ablenkung eines Lichtstrals von seiner ger-
adlinigen Bewegung, durch die Attraktion eines Weltkörpers, an
welchem er nahe vorbei geht. Berliner Astronomisches Jahrbuch,
161–172.cc (1804)
5. F.W. Dyson, A.S. Eddington, C. Davidson, A determination of the
deflection of light by the sun’s gravitational field, from observations
made at the total eclipse of May 29, 1919. Phil. Trans. R. Soc. Lond.
A 220, 291 (1920)
6. D. Valls-Gabaud, The conceptual origins of gravitational lensing.
AIP Conf. Proc. 861(1), 1163 (2006)
7. M. Bartelmann, P. Schneider, Weak gravitational lensing. Phys.
Rep. 340, 291 (2001)
8. M. Bartelmann, Gravitational lensing. Class. Quant. Gravit. 27,
233001 (2010)
9. C.R. Keeton, C.S. Kochanek, E.E. Falco, The optical properties
of gravitational lens galaxies as a probe of galaxy structure and
evolution. Astrophys. J. 509, 561 (1998)
10. E.F. Eiroa, G.E. Romero, D.F. Torres, Reissner–Nordstrom black
hole lensing. Phys. Rev. D 66, 024010 (2002)
11. S. Mao, B. Paczynski, Gravitational microlensing by double stars
and planetary systems. Astrophys. J. 374, L37 (1991)
12. V. Bozza, Gravitational lensing in the strong field limit. Phys. Rev.
D 66, 103001 (2002)
13. E. Gallo, O.M. Moreschi, Gravitational lens optical scalars in
terms of energy-momentum distributions. Phys. Rev. D 83, 083007
(2011)
14. G. Crisnejo, E. Gallo, Expressions for optical scalars and deflection
angle at second order in terms of curvature scalars. Phys. Rev. D
97(8), 084010 (2018)
15. M. Sharif, S. Iftikhar, Strong gravitational
lensing in non-
commutative wormholes. Astrophys. Space Sci. 357(1), 85 (2015)
16. G.W. Gibbons, M.C. Werner, Applications of the Gauss–Bonnet
theorem to gravitational lensing. Class. Quant. Gravit. 25, 235009
(2008)
17. M.C. Werner, Gravitational lensing in the Kerr–Randers optical
geometry. Gen. Relat. gravit. 44, 3047 (2012)
18. A. Ishihara, Y. Suzuki, T. Ono, T. Kitamura, H. Asada, Gravitational
bending angle of light for finite distance and the Gauss–Bonnet
theorem. Phys. Rev. D 94(8), 084015 (2016)
19. G. Crisnejo, E. Gallo, Weak lensing in a plasma medium and grav-
itational deflection of massive particles using the Gauss–Bonnet
theorem. A unified treatment. Phys. Rev. D 97(12), 124016 (2018)
Eur. Phys. J. C (2019) 79 :694
Page 7 of 7 694
20. K. Jusufi, M.C. Werner, A. Banerjee, A. Övgün, Light deflection
by a rotating global monopole spacetime. Phys. Rev. D 95(10),
104012 (2017)
21. I. Sakalli, A. Ovgun, Hawking radiation and deflection of light
from rindler modified schwarzschild black hole. EPL 118(6), 60006
(2017)
22. K. Jusufi, A. Övgün, Gravitational lensing by rotating wormholes.
Phys. Rev. D 97(2), 024042 (2018)
23. T. Ono, A. Ishihara, H. Asada, Gravitomagnetic bending angle of
light with finite-distance corrections in stationary axisymmetric
spacetimes. Phys. Rev. D 96(10), 104037 (2017)
24. K. Jusufi, A. Övgün, A. Banerjee, Light deflection by charged
wormholes in Einstein-Maxwell-dilaton theory. Phys. Rev. D
96(8), 084036 (2017)
25. A. Övgün, G. Gyulchev, K. Jusufi, Weak gravitational lensing by
phantom black holes and phantom wormholes using the Gauss–
Bonnet theorem. Ann. Phys. 406, 152 (2019)
26. K. Jusufi, I. Sakalli, A. Övgün, Effect of lorentz symmetry breaking
on the deflection of light in a cosmic string spacetime. Phys. Rev.
D 96(2), 024040 (2017)
27. H. Arakida, Light deflection and GaussBonnet theorem: definition
of total deflection angle and its applications. Gen. Relat. Gravit.
50(5), 48 (2018)
28. T. Ono, A. Ishihara, H. Asada, Deflection angle of light for an
observer and source at finite distance from a rotating wormhole.
Phys. Rev. D 98(4), 044047 (2018)
29. K. Jusufi, A. Övgün, Effect of the cosmological constant on the
deflection angle by a rotating cosmic string. Phys. Rev. D 97(6),
064030 (2018)
30. A. Övgün, K. Jusufi, I. Sakalli, Exact traversable wormhole solution
in bumblebee gravity. Phys. Rev. D 99(2), 024042 (2019)
31. K. Jusufi, A. Övgün, J. Saavedra, Y. Vasquez, P.A. Gonzalez,
Deflection of light by rotating regular black holes using the Gauss–
Bonnet theorem. Phys. Rev. D 97(12), 124024 (2018)
32. A. Övgün, Light deflection by Damour–Solodukhin wormholes
and Gauss–Bonnet theorem. Phys. Rev. D 98(4), 044033 (2018)
33. A. Övgün, K. Jusufi, I. Sakalli, Gravitational lensing under the
effect of Weyl and bumblebee gravities: applications of Gauss–
Bonnet theorem. Ann. Phys. 399, 193 (2018)
34. A. Övgün, Deflection angle of photon through dark matter by black
holes and wormholes using the Gauss–Bonnet theorem. Universe
5(5), 115 (2019)
35. A. Övgün, I. Sakalli, J. Saavedra, Weak gravitational
lens-
theorem.
ing by Kerr–MOG black hole and Gauss–Bonnet
arXiv:1806.06453 [gr-qc]
36. A. Övgün, I. Sakalli, J. Saavedra, Shadow cast and deflection angle
of Kerr–Newman–Kasuya spacetime. JCAP 1810(10), 041 (2018)
37. T. Ono, A. Ishihara, H. Asada, Deflection angle of light for
an observer and source at finite distance from a rotating global
monopole. Phys. Rev. D 99(12), 124030 (2019)
38. A. Övgün, Weak gravitational lensing of regular black holes with
cosmic strings using the Gauss–Bonnet theorem. Phys. Rev. D
99(10), 104075 (2019)
39. Wajiha Javed, Rimsha Babar, A. Övgün, The effect of the Brane–
Dicke coupling parameter on weak gravitational lensing by worm-
holes and naked singularities. Phys. Rev. D 99(8), 084012 (2019)
40. A. Övgün, ˙I. Sakallı, Deriving Hawking radiation via Gauss-
Bonnet Theorem: an alternative way. arXiv:1902.04465 [hep-th]
41. S.I. Kruglov, Magnetized black holes and nonlinear electrodynam-
ics. Int. J. Mod. Phys. A 32(23n24), 1750147 (2017)
42. S.I. Kruglov, On a model of magnetically charged black hole with
nonlinear electrodynamics. Universe 4(5), 66 (2018)
43. S.I. Kruglov, Nonlinear electrodynamics and magnetic black holes.
Ann. Phys. 529(8), 1700073 (2017)
44. S.I. Kruglov, BornInfeld-type electrodynamics and magnetic black
holes. Ann. Phys. 383, 550 (2017)
45. S.I. Kruglov, Black hole as a magnetic monopole within exponen-
tial nonlinear electrodynamics. Ann. Phys. 378, 59 (2017)
46. S.I. Kruglov, Notes on BornInfeld-type electrodynamics. Mod.
Phys. Lett. A 32(36), 1750201 (2017)
47. S.I. Kruglov, Asymptotic Reissner–Nordstrm solution within non-
linear electrodynamics. Phys. Rev. D 94(4), 044026 (2016)
48. S.I. Kruglov, Nonlinear arcsin-electrodynamics and asymptotic
Reissner–Nordstrm black holes. Ann. Phys. 528, 588 (2016)
49. M. Novello, V.A. De Lorenci, J.M. Salim, R. Klippert, Geometrical
aspects of light propagation in nonlinear electrodynamics. Phys.
Rev. D 61, 045001 (2000)
50. M. Novello, J.M. Salim, V.A. De Lorenci, E. Elbaz, Nonlinear elec-
trodynamics can generate a closed space—like path for photons.
Phys. Rev. D 63, 103516 (2001)
51. K.A. Bronnikov, Regular magnetic black holes and monopoles
from nonlinear electrodynamics. Phys. Rev. D 63, 044005 (2001)
52. E. Ayon-Beato, A. Garcia, Regular black hole in general relativity
coupled to nonlinear electrodynamics. Phys. Rev. Lett. 80, 5056
(1998)
53. E. Ayon-Beato, A. Garcia, Nonsingular charged black hole solution
for nonlinear source. Gen. Relat. Gravit. 31, 629 (1999)
54. M.E. Rodrigues, MVdS Silva, Bardeen regular black hole with an
electric source. JCAP 1806(06), 025 (2018)
55. S.A. Hayward, Formation and evaporation of regular black holes.
Phys. Rev. Lett. 96, 031103 (2006)
56. A.N. Aliev, D.V. Galtsov, Magnetized black holes. Sov. Phys. Usp.
32, 75 (1989)
57. A.N. Aliev, Rotating black holes in higher dimensional Einstein–
Maxwell gravity. Phys. Rev. D 74, 024011 (2006)
58. A.N. Aliev, Gyromagnetic ratio of charged Kerr-Anti-de sitter
black holes. Class. Quant. Gravit. 24, 4669 (2007)
59. A.N. Aliev, V.P. Frolov, Five-dimensional rotating black hole in a
uniform magnetic field: the gyromagnetic ratio. Phys. Rev. D 69,
084022 (2004)
60. A.N. Aliev, N. Ozdemir, Motion of charged particles around a rotat-
ing black hole in a magnetic field. Mon. Not. R. Astron. Soc. 336,
241 (2002)
61. D. Bao, S. Chern, Z. Shen, An introduction to Riemann–Finsler
geometry (Springer, New York, 2000)
62. B. Paczynski, Gravitational microlensing by the galactic halo.
Astrophys. J. 304, 1 (1986)
63. C. Alcock et al. [Supernova Cosmology Project Collaboration],
Possible Gravitational Microlensing of a Star in the Large Magel-
lanic Cloud. Nature 365, 621 (1993)
64. E. Aubourg et al., Evidence for gravitational microlensing by dark
objects in the galactic halo. Nature 365, 623 (1993)
65. A. Udalski, M. Szymanski, J. Kaluzny, M. Kubiak, W. Krzeminski,
M. Mateo, G.W. Preston, B. Paczynski, The optical gravitational
lensing experiment. Discovery of the first candidate microlensing
event in the direction of the Galactic Bulge. Acta Astron. 43, 289
(1993)
66. V.P. Frolov, Weakly magnetized black holes as particle accelerators.
Phys. Rev. D 85, 024020 (2012)
67. J. Liang, Regular magnetic black hole gravitational lensing. Chin.
Phys. Lett. 34(5), 050401 (2017)
68. B. Turimov, B. Ahmedov, A. Abdujabbarov, C. Bambi, Gravita-
tional lensing by magnetized compact object in the presence of
plasma. arXiv:1802.03293 [gr-qc]
123
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
