论文研究-支持向量机在步态分类中的应用 .pdf-资料库

weixin_39840387-11579705-4744302542959381352.pdf-第1页.png

第1页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第2页.png

第2页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第3页.png

第3页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第4页.png

第4页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第5页.png

第5页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第6页.png

第6页 / 共7页

weixin_39840387-11579705-4744302542959381352.pdf-第7页.png

第7页 / 共7页

http://www.paper.edu.cn 支持向量机在步态分类中的应用张云 1 1 大连理工大学自动化系，辽宁大连(116023) E-mail：zy087763@163.com 摘要：由 Vapnik 及其合作者提出的支持向量机(Support Vector Machine, SVM)是一种新型机器学习方法，因其出色的学习能力，已成为当前国际机器学习界的研究热点。目前支持向量机已应用于模式分类、回归分析、函数估计等方面。本文将支持向量机应用到儿童异常步态分析，拓宽了支持向量机的应用范围，促进了学科间的交叉。为了提高准确率，本文提出了基于模糊聚类和支持向量机方法对儿童步态分类。经过仿真实验，证明该方法的有效性。关键词：统计学习理论；支持向量机；分类；模糊聚类；步态中图分类号： TP181 1. 引言在康复、医疗领域,步态分析在步态疾病的早期诊断、治疗效果及康复评估中具有特别重要的意义。临床上,步态分析系统测量的步态参数均以大量的曲线图表示,医生通过视觉观察患者的步态和比较曲线图中的步态参数差异,评估患者的步态变化,这种评估结果极为主观。为了客观评价步态变化,人工智能技术已经在步态分类中得到广泛应用。近年来,机器学习在步态分类中越来越受到重视[1]。目前,人工神经网络由于具有很强的非线性映射能力和学习能力,在正常和病理步态分类中得到了应用,并取得了很好的效果[2]。然而,由于神经网络遵循的是基于训练样本的训练误差最小化原则,在学习过程中,可能陷入局部极小值,并容易过度拟合训练样本,降低分类器的泛化精度。而且步态数据采集过程比较繁琐、费时,获取的数据样本量少。这些因素将严重影响神经网络分类器的步态分类性能。针对上述问题，本文提出了基于模糊聚类的支持向量机方法，并将此方法用于步态分析。通过对学习样本的聚类，选用同类特征数据作为模型的预测输入，然后对各个模型的输入数据进行归一化处理和分类识别，得出最后总的预测输出。此预测方法保证了数据特征的一致性以及算法的全局性，避免了算法陷入局部极小的缺陷。经过仿真实验，证明了该方法的有效性。 2. 支持向量机原理支持向量机[3]主要是基于如下思想:通过事先选择的非线性映射将输入向量映射到高维特征空间, 在这个空间中构造最优决策函数。在构造最优决策函数时,利用了结构风险最小化原则,同时引入了间隔的概念。并巧妙地利用原空间的核函数取代了高维特征空间中的点积运算,避免了复杂计算。目前支持向量机算法主要有分类和估计等。该文讨论的是分类算法。识别不同步态模式,其本质上是一个二分类问题,假设步态样本训练 x ∈i dR F =D {( i yx , i )} l i 1 = ,每个输入向 ,映射到高维特征空间 ,步态分类器就是在高维特征空间中找 , 和b 为权向量和偏置,它能够将步态数据空间中的样本映射 w 1{ 。 }1,+−∈iy 量到一个最优线性分类面 ,通过非线性函数 xf )( )(x z ϕ= bxw +⋅= 到其相应的类标志空间,相应的输出 1

http://www.paper.edu.cn 目前,利用支持向量机构造最优线性分类面有硬间隔、软间隔等多种形式。如何在高维空间中构造最优线性分类面是步态分类器的关键问题。在步态数据采集过程中,由于受人体运动和周围环境的影响, 数据中含有大量的噪声。为了更好地减少步态样本训练误差,引入松驰变量,通过求解下列优化问题,寻找最优分类面。 min 1 2 2 w C ⋅+ n ∑ i 1 = ξ ， s.t. i xwy ⋅ i ( i + b 1) ξ−≥ i (1) 其中 C 是用户自定义的惩罚因子。利用 Lagrange 乘子法把公式（1）变成其对偶形式，即： max Q )( =∂ n ∑ i 1 = −∂ i 1 2 n ∑ ∂∂ i 1 = ji , yy i j ( xx i j ) j （2） s.t n ∂∑ i 1 = i y i = 0 ， i ∈∂ ,0[ C ] , i = ( ,...,2,1 n ) 式中为与每个样本对应的 Lagrange 乘子，若 i∂ 0≠∂ i ，则称训练样本为支持向量。判决函数为： ix xf )( = sgn( xw ⋅ i + b ) = sgn[ n ∑ i 1 = ∂ i xy ( i i ⋅ x ) + b ] （3）对于非线性可分的问题，可以通过核函数把输入空间映射到某高维特征空间，在特征空间进行分类。利用核函数 ,K( yx ) = 为： ϕϕ ⋅ x )( y )( ，满足 Mercer 定理，求解出上述优化问题的最优解。其判别函数 xf )( = sgn( xw ⋅ i + b ) = sgn[ 3. 支持向量机改进算法 n ∑ i 1 = ∂ i y i K( x i ⋅ x ) + b ] （4）本章提出一种数据预处理的方法，在传统支持向量机(SVM)基础上，通过对学习样本集进行模糊 C 均值聚类，然后根据聚类的结果对不同的类别采用不同的支持向量机进行描述，再由样本点到各个聚类中心的距离来确定输入对每个 SVM 模型的隶属度，最后综合得到整个分布式 SVM 的输出。 3.1 模糊C均值聚类聚类中允许每一个样本以不同的隶属程度分别属于不同的类，这就是模糊聚类算法。模糊 C 均值聚类算法(FCM)基于误差平方和目标函数准则，是一种简单常用的典型动态聚类算法，在图像处理、数据挖掘、人工智能等方面均有较多应用。在样本集中随机选择 c 个点作为聚类中心，优化如下目标函数 J VU ( , ) = c n ∑∑ k 1 = i 1 = d μ ik x k − v i 2 （5） 2

http://www.paper.edu.cn 式中 d 为模糊控制参数，n 为数据个数，c 为类别数，隶属度 = μU nt× ，满足 ]1,0[∈ikμ 和 1=∑ ikμ 。通过反复迭代，使误差平方和目标函数达到最小。 FCM 算法可按下列步骤来完成：（1）首先确定参数： m (加权指数)，ε(收敛门限)， )0(U (初始划分)， (样本数目)， (聚类数目 C ≤2 lC ≤ ) 。 l （2）进行初始模糊 C 划分，得到 )0(U 。（3）计算聚类中心 iV { )(b } ，b 为迭代次数，为第 k 个数据的输入值， kx b )( V i m ) x k ,...3,2,1=b i ,...,2,1,0= c （6） l k ∑ ( μ ik 1 == m ∑ ( μ ik k 1 = m ) （4）对 )(bU 进行修正，计算中的 ( +bU )1 如下： μ ik = c ∑ j 1 = （7） 1 ( d d ik jk m )1 − (2) （5）若 U b U )( − ( b + )1 ε≤ ，停止迭代，否则 1+= bb ，并返回到步骤 3。 3.3 基于模糊C均值聚类的支持向量机本节提出的基于模糊 C 均值聚类的支持向量机（FCMSVM）的具体算法步骤如下：（1）对获取历史数据进行归一化和预处理。（2）建立训练样本集和预测样本集。（3）用FCM算法聚类。（4）识别预测样本所属类（5）建立SVM预测模型。别。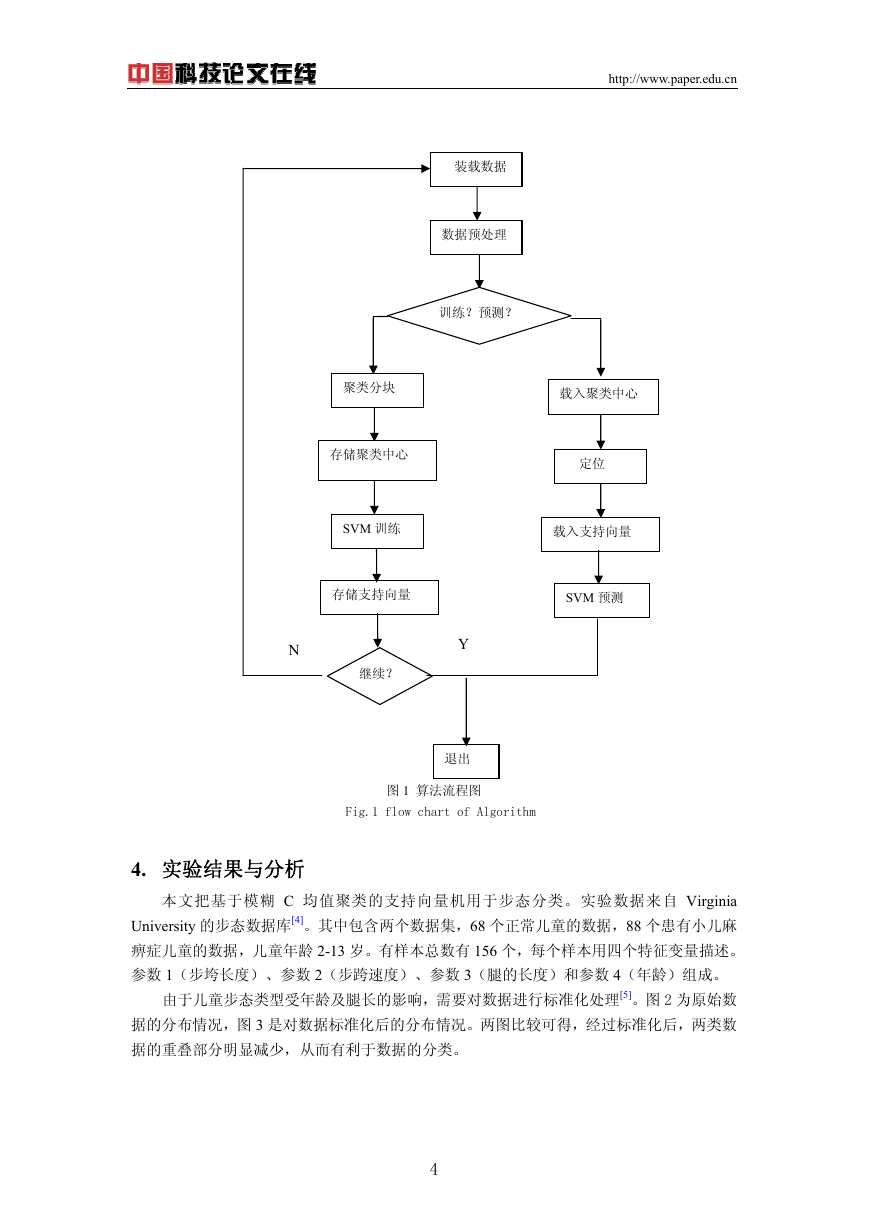图 1 为算法流程图： 3

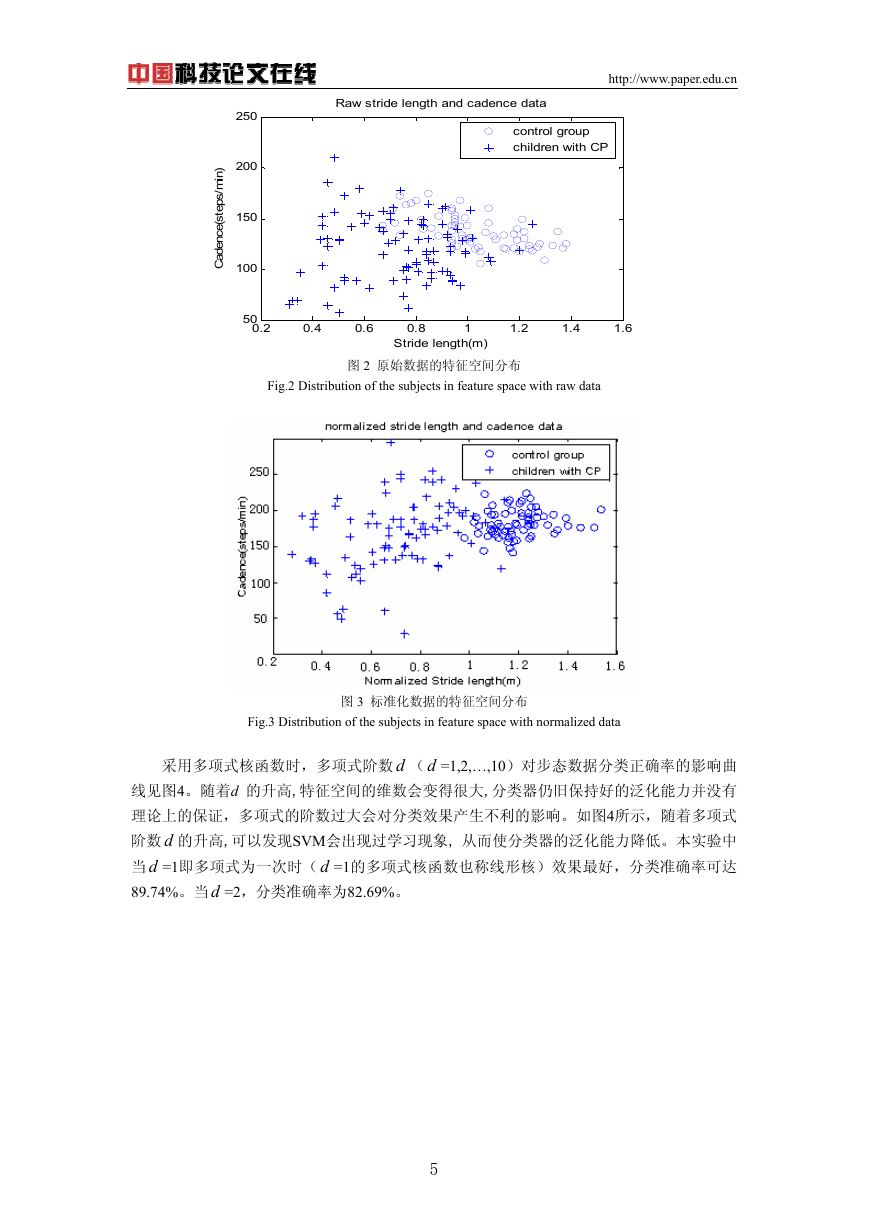
http://www.paper.edu.cn 装载数据数据预处理训练？预测？ Y 退出载入聚类中心定位载入支持向量 SVM 预测聚类分块存储聚类中心 SVM 训练存储支持向量 N 继续？图 1 算法流程图 Fig.1 flow chart of Algorithm 4. 实验结果与分析本文把基于模糊 C 均值聚类的支持向量机用于步态分类。实验数据来自 Virginia University 的步态数据库[4]。其中包含两个数据集，68 个正常儿童的数据，88 个患有小儿麻痹症儿童的数据，儿童年龄 2-13 岁。有样本总数有 156 个，每个样本用四个特征变量描述。参数 1（步垮长度）、参数 2（步跨速度）、参数 3（腿的长度）和参数 4（年龄）组成。由于儿童步态类型受年龄及腿长的影响，需要对数据进行标准化处理[5]。图 2 为原始数据的分布情况，图 3 是对数据标准化后的分布情况。两图比较可得，经过标准化后，两类数据的重叠部分明显减少，从而有利于数据的分类。 - 4 - 4

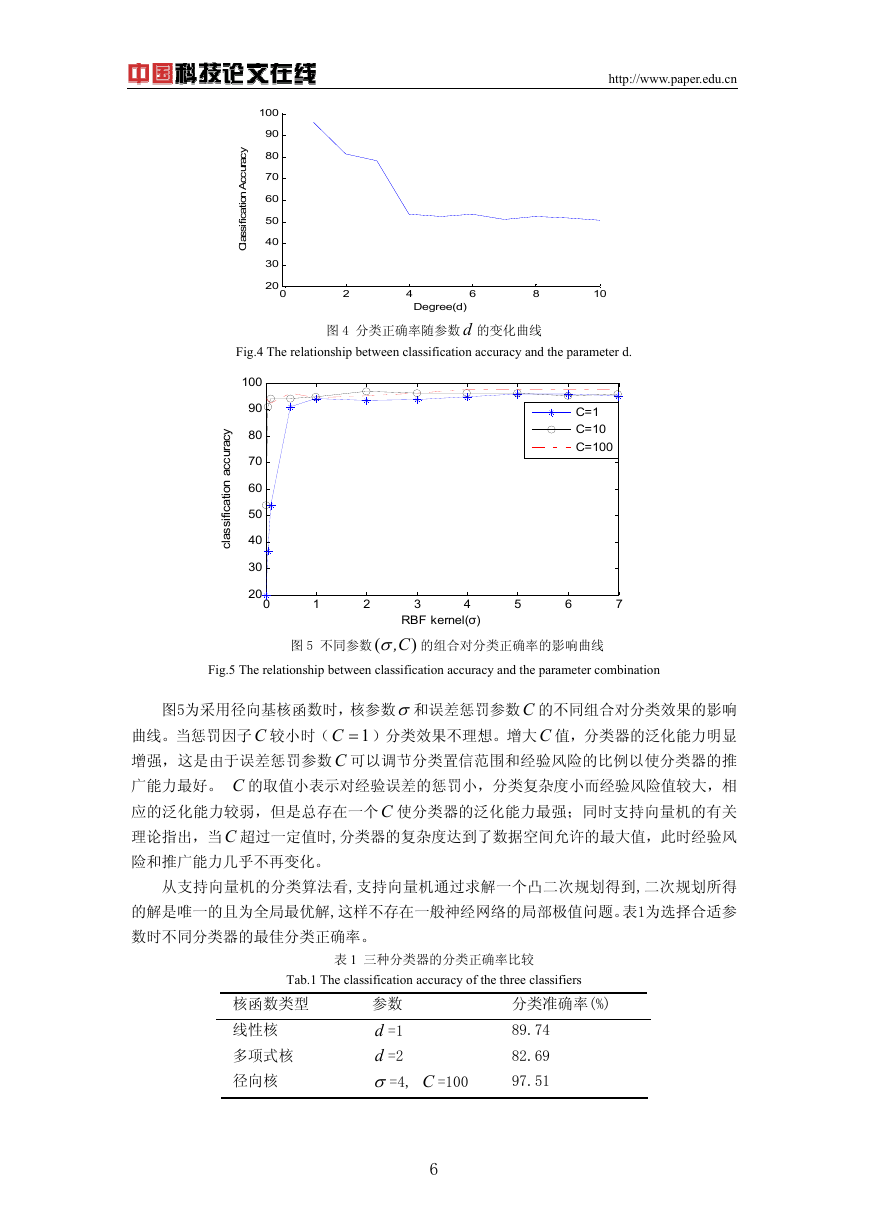
http://www.paper.edu.cn Raw stride length and cadence data control group children with CP 250 200 150 100 ) n mi / s p e t s ( e c n e d a C 50 0.2 0.4 0.6 0.8 1 Stride length(m) 1.2 1.4 1.6 图 2 原始数据的特征空间分布 Fig.2 Distribution of the subjects in feature space with raw data 图 3 标准化数据的特征空间分布 Fig.3 Distribution of the subjects in feature space with normalized data d d 采用多项式核函数时，多项式阶数（ =1,2,…,10）对步态数据分类正确率的影响曲线见图4。随着d 的升高,特征空间的维数会变得很大,分类器仍旧保持好的泛化能力并没有理论上的保证，多项式的阶数过大会对分类效果产生不利的影响。如图4所示，随着多项式阶数的升高,可以发现SVM会出现过学习现象, 从而使分类器的泛化能力降低。本实验中当 =1即多项式为一次时（ d =1的多项式核函数也称线形核）效果最好，分类准确率可达 89.74%。当d =2，分类准确率为82.69%。 d d - 5 - 5

y c a r u c c A n o i t a c i f i s s a Cl 100 90 80 70 60 50 40 30 20 0 2 4 http://www.paper.edu.cn 8 10 图 4 分类正确率随参数的变化曲线 Fig.4 The relationship between classification accuracy and the parameter d. 6 Degree(d) d y c a r u c c a n o i t a c i f i s s a c l 100 90 80 70 60 50 40 30 20 0 1 2 图 5 不同参数 C=1 C=10 C=100 5 6 7 3 4 RBF kernel(σ) ) ( C,σ 的组合对分类正确率的影响曲线 Fig.5 The relationship between classification accuracy and the parameter combination 图5为采用径向基核函数时，核参数σ和误差惩罚参数的不同组合对分类效果的影响）分类效果不理想。增大C 值，分类器的泛化能力明显增强，这是由于误差惩罚参数可以调节分类置信范围和经验风险的比例以使分类器的推曲线。当惩罚因子较小时（ 1=C C C C 广能力最好。的取值小表示对经验误差的惩罚小，分类复杂度小而经验风险值较大，相 C 应的泛化能力较弱，但是总存在一个使分类器的泛化能力最强；同时支持向量机的有关 C 理论指出，当超过一定值时,分类器的复杂度达到了数据空间允许的最大值，此时经验风 C 险和推广能力几乎不再变化。从支持向量机的分类算法看,支持向量机通过求解一个凸二次规划得到,二次规划所得的解是唯一的且为全局最优解,这样不存在一般神经网络的局部极值问题。表1为选择合适参数时不同分类器的最佳分类正确率。表 1 三种分类器的分类正确率比较 Tab.1 The classification accuracy of the three classifiers 核函数类型线性核多项式核径向核参数 d =1 d =2 σ=4, C =100 分类准确率(%) 89.74 82.69 97.51 - 6 - 6

http://www.paper.edu.cn 5. 结论基于模糊聚类的支持向量机方法，对输入样本进行模糊聚类分析，只采用与预测样本特征相似的样本作为训练样本建立支持向量机预测模型，减少了运算时间，提高了识别率。实验结果表明，该方法能够有效地识别步态变化,较好地解决小样本步态数据在步态分类中泛化能力差的问题。在支持向量机算法中,采用不同的核函数得到不同的支持向量机算法,究竟采用哪一种最适合的核函数,使分类性能最优,目前并没有确切的定论。一般情况下,需要反复实验确定。实验中,通过使用采集的步态数据,我们比较了线性核、多项式核和径向基核函数分类器的分类性能,结果表明,径向基核分类器的分类性能较好。参考文献 [1] Simon.S.R. Quantification of human motion: gait analysis-benefits and limitations to its application to clinical problems[J]. Journal of Biomechanics, 2004(37): 1869-1880. [2] Barton.J.G, Lees A. An application of neural networks for distinguishing gait patterns on the basi s of hip-knee joint angle diagrams[J]. Gait and Posture, 1997(5): 28-33. [3] 张学工译.统计学习理论的本质.北京:清华大学出版社,2000,1-226 [4] M.J.O’Malley, M.F.Abel,D.L.Damiano, and C.L.Vaughan, “Fuzzy clustering of children with cerebr al palsy based on temporal-distance gait parameters,” IEEE Trans.Rehab.Eng.,vol.5,no.4,pp.300–309, Dec.1997. [5] M.J.O’Malley, “Normalization of temporal-distance parameters in parameters paediatric gait,” J.Bio mech.,vol.29,no.5,pp.619–625,1996. Research Support Vector Machine and Its Application in Gait Classification 1 Electronic and Information Engineering School ,Dalian University of Technology, Dalian ZHANG Yun 1 (116023) Abstract Support Vector Machine(SVM),developed by Vapnik, as a novel type of machine learning method, has become the hotspot of machine learning because of its rigorous theory background and remarkable generalization performance. The recent researches on SVM mainly concentrated on the property of SVM and diversity and depth of its applications. In this paper, support vector machine is applied to children's abnormal gait analysis, which expands the SVM application, and strengthens the intercrossing of subjects. In order to improve the accuracy, the new algorithm is combined with fuzzy clustering and support vector machines for children gait analysis. After the experiment, it proves the effectiveness. Key words: statistical learning theory；support vector machine；classification； fuzzy clustering； gait - 7 - 7

资料库

论文研究-支持向量机在步态分类中的应用 .pdf

相关推荐

开发技术

热门标签

最新资料