Python概率分布大全（含可视化）.pdf-资料库

weixin_38748718-13742385-16359647480740012449.pdf-第1页.png

第1页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第2页.png

第2页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第3页.png

第3页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第4页.png

第4页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第5页.png

第5页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第6页.png

第6页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第7页.png

第7页 / 共41页

weixin_38748718-13742385-16359647480740012449.pdf-第8页.png

第8页 / 共41页

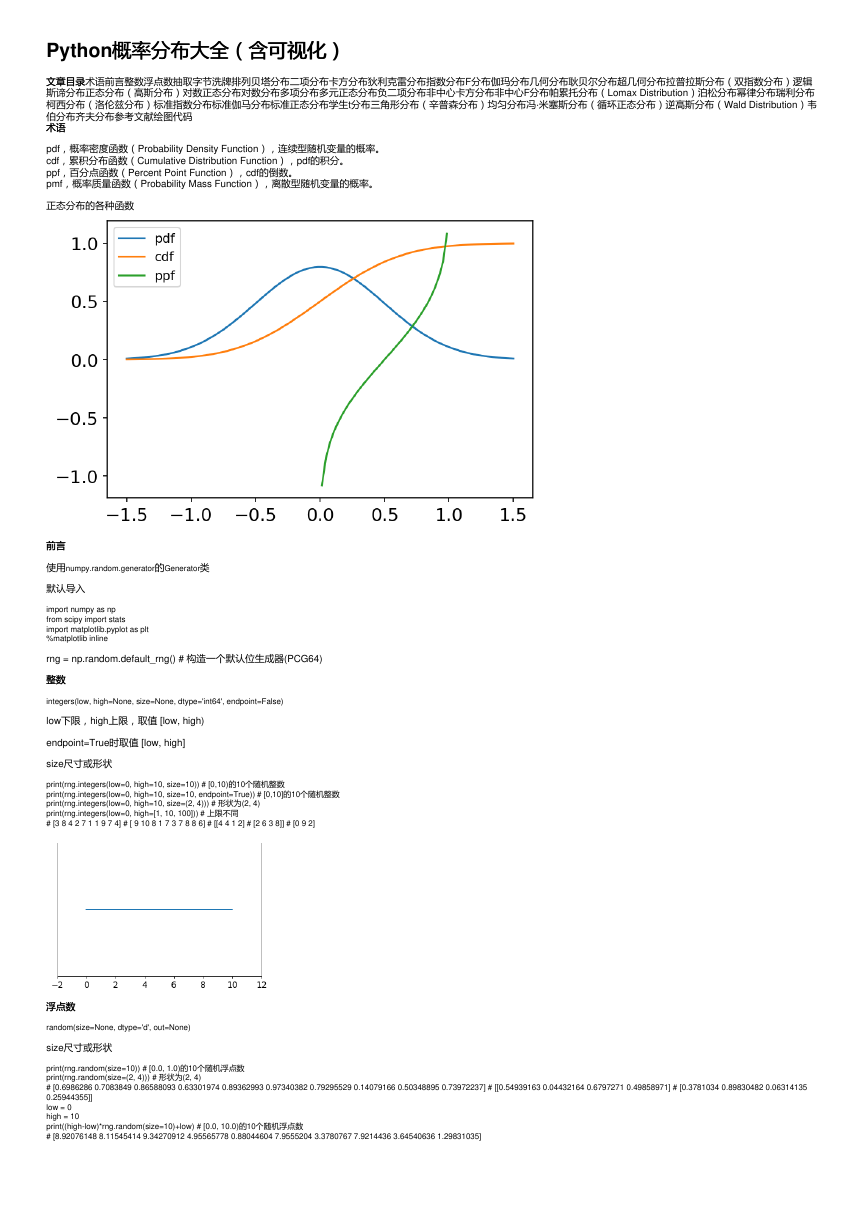
Python概率分布大全（含可视化）概率分布大全（含可视化）文章目录术语前言整数浮点数抽取字节洗牌排列贝塔分布二项分布卡方分布狄利克雷分布指数分布F分布伽玛分布几何分布耿贝尔分布超几何分布拉普拉斯分布（双指数分布）逻辑文章目录斯谛分布正态分布（高斯分布）对数正态分布对数分布多项分布多元正态分布负二项分布非中心卡方分布非中心F分布帕累托分布（Lomax Distribution）泊松分布幂律分布瑞利分布柯西分布（洛伦兹分布）标准指数分布标准伽马分布标准正态分布学生t分布三角形分布（辛普森分布）均匀分布冯·米塞斯分布（循环正态分布）逆高斯分布（Wald Distribution）韦伯分布齐夫分布参考文献绘图代码术语术语 pdf，概率密度函数（Probability Density Function），连续型随机变量的概率。 cdf，累积分布函数（Cumulative Distribution Function），pdf的积分。 ppf，百分点函数（Percent Point Function），cdf的倒数。 pmf，概率质量函数（Probability Mass Function），离散型随机变量的概率。正态分布的各种函数前言前言使用numpy.random.generator的Generator类默认导入 import numpy as np from scipy import stats import matplotlib.pyplot as plt %matplotlib inline rng = np.random.default_rng() # 构造一个默认位生成器(PCG64) 整数整数 integers(low, high=None, size=None, dtype='int64', endpoint=False) low下限，high上限，取值 [low, high) endpoint=True时取值 [low, high] size尺寸或形状 print(rng.integers(low=0, high=10, size=10)) # [0,10)的10个随机整数 print(rng.integers(low=0, high=10, size=10, endpoint=True)) # [0,10]的10个随机整数 print(rng.integers(low=0, high=10, size=(2, 4))) # 形状为(2, 4) print(rng.integers(low=0, high=[1, 10, 100])) # 上限不同 # [3 8 4 2 7 1 1 9 7 4] # [ 9 10 8 1 7 3 7 8 8 6] # [[4 4 1 2] # [2 6 3 8]] # [0 9 2] 浮点数浮点数 random(size=None, dtype='d', out=None) size尺寸或形状 print(rng.random(size=10)) # [0.0, 1.0)的10个随机浮点数 print(rng.random(size=(2, 4))) # 形状为(2, 4) # [0.6986286 0.7083849 0.86588093 0.63301974 0.89362993 0.97340382 0.79295529 0.14079166 0.50348895 0.73972237] # [[0.54939163 0.04432164 0.6797271 0.49858971] # [0.3781034 0.89830482 0.06314135 0.25944355]] low = 0 high = 10 print((high-low)*rng.random(size=10)+low) # [0.0, 10.0)的10个随机浮点数 # [8.92076148 8.11545414 9.34270912 4.95565778 0.88044604 7.9555204 3.3780767 7.9214436 3.64540636 1.29831035]

抽取抽取 choice(a, size=None, replace=True, p=None, axis=0) a 抽取范围 int或1维数组 size尺寸或形状 replace是否放回原处 p 每个元素的抽取概率 1维数组 print(rng.choice(a=10, size=3)) # [0,10)的3个随机整数，a=10调用了np.arange(10)，相当于rng.integers(low=0, high=10, size=3) print(rng.integers(low=0, high=10, size=3)) # [2 6 0] # [8 4 4] print(rng.choice(a=[1,2,3,4,5], size=5)) # 从中抽3个 print(rng.choice(a=[1,2,3,4,5], size=5, replace=False)) # 不放回 # [1 2 2 5 2] # [5 4 1 3 2] 字节字节 bytes(length) print(rng.bytes(10)) # b'\xf7\x8f@{\x9d\xbb\xdfk\x9c\x97' 洗牌洗牌 shuffle(x)返回空值，影响原数组 l = np.arange(10) # list也行 print(l) rng.shuffle(l) print(l) # [0 1 2 3 4 5 6 7 8 9] # [6 8 9 2 0 3 5 4 7 1] 排列排列 permutation(x)类似洗牌，只影响最外层 x int或数组 print(rng.permutation(10)) # 随机排列0-9的数组 print(rng.permutation(np.arange(10))) #同上 # [7 8 6 0 2 1 9 3 4 5] # [0 5 7 2 8 6 4 3 9 1] arr = np.arange(9).reshape((3, 3)) print(arr) print(rng.permutation(arr)) # 只影响最外层的顺序 print(arr) # [[0 1 2] # [3 4 5] # [6 7 8]] # [[3 4 5] # [6 7 8] # [0 1 2]] # [[0 1 2] # [3 4 5] # [6 7 8]] 贝塔分布贝塔分布 beta(a, b, size=None) 贝塔分布是狄利克雷分布的特例，与伽马分布有关。贝塔分布是伯努利分布和二项式分布的共轭先验分布的密度函数，也称B分布，是一组定义在(0,1)的连续概率分布（概率的概率分布概率的概率分布）。概率分布函数： f(x;α,β)=1B(α,β)xα−1(1−x)β−1f\left( x;\alpha ,\beta \right) =\frac{1}{\text{B}\left( \alpha ,\beta \right)}x^{\alpha -1}\left( 1-x \right) ^{\beta -1}f(x;α,β)=B(α,β)1xα−1(1−x)β−1 随机变量XXX服从参数为α,β\alpha ,\betaα,β的B分布写作

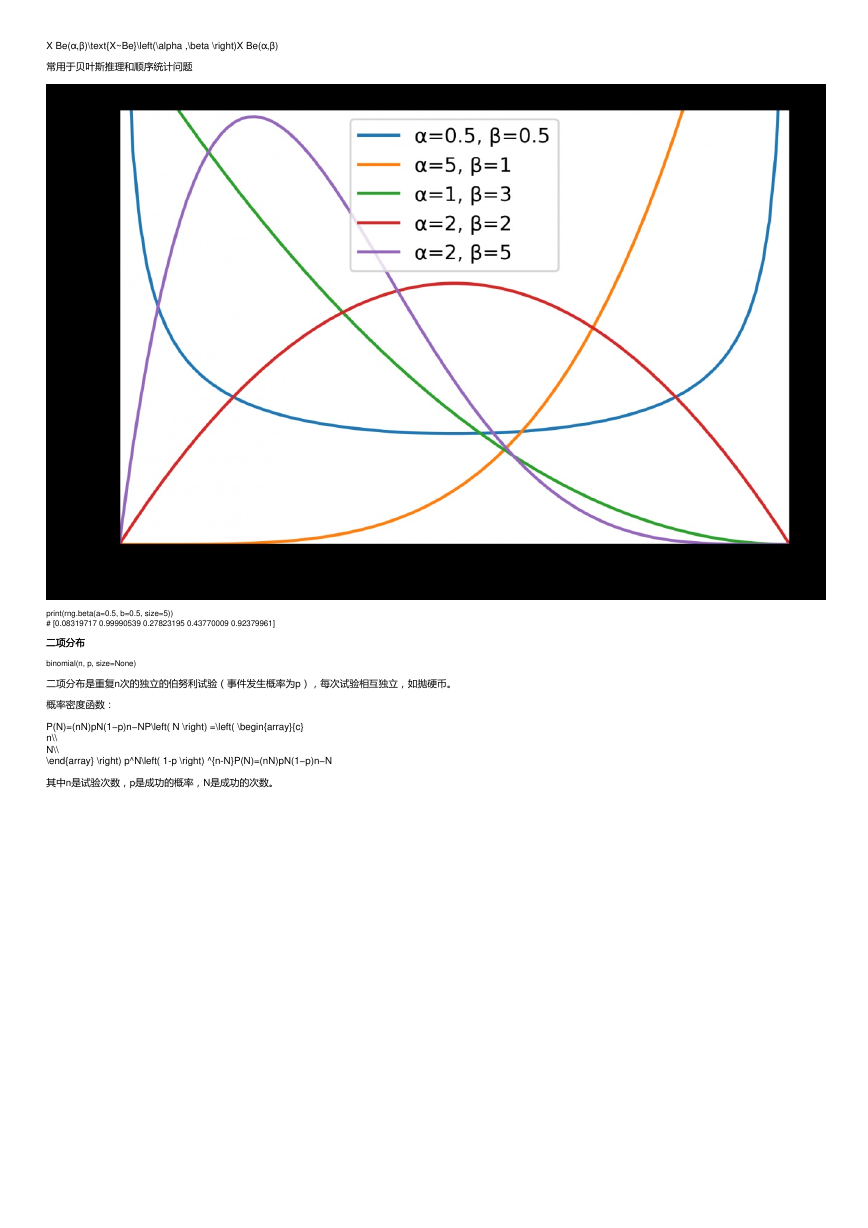
X Be(α,β)\text{X~Be}\left(\alpha ,\beta \right)X Be(α,β) 常用于贝叶斯推理和顺序统计问题 print(rng.beta(a=0.5, b=0.5, size=5)) # [0.08319717 0.99990539 0.27823195 0.43770009 0.92379961] 二项分布二项分布 binomial(n, p, size=None) 二项分布是重复n次的独立的伯努利试验（事件发生概率为p），每次试验相互独立，如抛硬币。概率密度函数： P(N)=(nN)pN(1−p)n−NP\left( N \right) =\left( \begin{array}{c} n\\ N\\ \end{array} \right) p^N\left( 1-p \right) ^{n-N}P(N)=(nN)pN(1−p)n−N 其中n是试验次数，p是成功的概率，N是成功的次数。

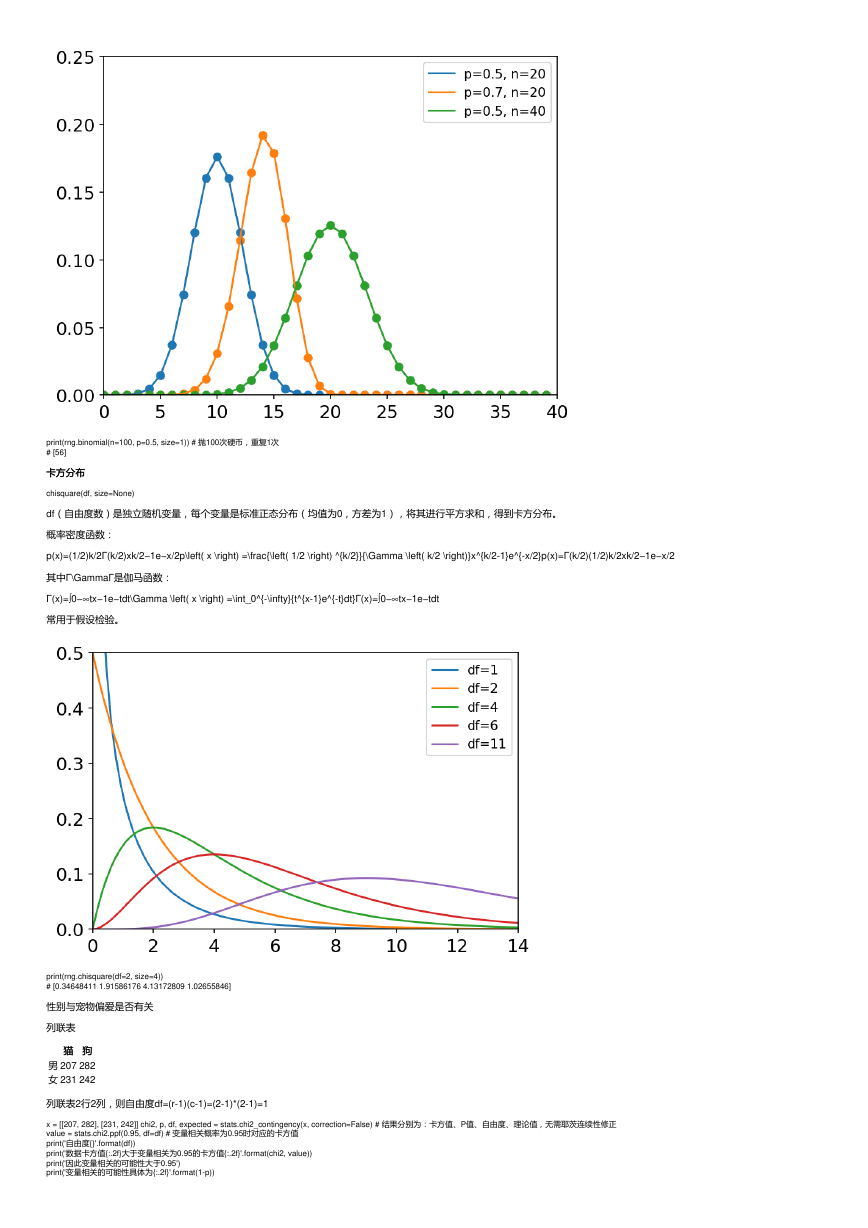
print(rng.binomial(n=100, p=0.5, size=1)) # 抛100次硬币，重复1次 # [56] 卡方分布卡方分布 chisquare(df, size=None) df（自由度数）是独立随机变量，每个变量是标准正态分布（均值为0，方差为1），将其进行平方求和，得到卡方分布。概率密度函数： p(x)=(1/2)k/2Γ(k/2)xk/2−1e−x/2p\left( x \right) =\frac{\left( 1/2 \right) ^{k/2}}{\Gamma \left( k/2 \right)}x^{k/2-1}e^{-x/2}p(x)=Γ(k/2)(1/2)k/2xk/2−1e−x/2 其中Γ\GammaΓ是伽马函数： Γ(x)=∫0−∞tx−1e−tdt\Gamma \left( x \right) =\int_0^{-\infty}{t^{x-1}e^{-t}dt}Γ(x)=∫0−∞tx−1e−tdt 常用于假设检验。 print(rng.chisquare(df=2, size=4)) # [0.34648411 1.91586176 4.13172809 1.02655846] 性别与宠物偏爱是否有关列联表猫猫狗狗男 207 282 女 231 242 列联表2行2列，则自由度df=(r-1)(c-1)=(2-1)*(2-1)=1 x = [[207, 282], [231, 242]] chi2, p, df, expected = stats.chi2_contingency(x, correction=False) # 结果分别为：卡方值、P值、自由度、理论值，无需耶茨连续性修正 value = stats.chi2.ppf(0.95, df=df) # 变量相关概率为0.95时对应的卡方值 print('自由度{}'.format(df)) print('数据卡方值{:.2f}大于变量相关为0.95的卡方值{:.2f}'.format(chi2, value)) print('因此变量相关的可能性大于0.95') print('变量相关的可能性具体为{:.2f}'.format(1-p))

# 自由度1 # 数据卡方值4.10大于变量相关为0.95的卡方值3.84 # 因此变量相关的可能性大于0.95 # 变量相关的可能性具体为0.96 狄利克雷分布狄利克雷分布狄利克雷分布是贝塔分布在高维的推广，常作为贝叶斯统计的先验概率。概率密度函数： Dir(X|α)=1B(α)∏i−1Kxiαi−1\text{Dir}\left( \text{X|}\alpha \right) =\frac{1}{\text{B}\left( \alpha \right)}\prod_{i-1}^K{x_{i}^{\alpha _i-1}}Dir(X|α)=B(α)1∏i−1Kxiαi−1 B(α)=∏i−1KΓ(αi)Γ(∑i=1Kαi)\text{B}\left( \alpha \right) =\frac{\prod_{i-1}^{\text{K}}{\Gamma \left( \alpha _i \right)}}{\Gamma \left( \sum_{i=1}^{\text{K}}{\alpha _i} \right)}B(α)=Γ(∑i=1K αi)∏i−1KΓ(αi) α=(α1,…,αK)\alpha =\left( \alpha _1,…,\alpha _{\text{K}} \right)α=(α1,…,αK) 常用于自然语言处理，特别是主题模型的研究。 print(rng.dirichlet(alpha=(10, 5, 3), size=3)) # [[0.45682216, 0.15384054, 0.3893373 ], # [0.41066417, 0.35596082, 0.23337501], # [0.62489734, 0.17707421, 0.19802845]] 指数分布指数分布 exponential(scale=1.0, size=None) 指数分布是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。概率密度函数： f(x;λ)=λe−λx, x≥0f\left( x;\lambda \right) =\lambda e^{-\lambda x},\ x\ge 0f(x;λ)=λe−λx, x≥0 其中λ\lambdaλ为单位时间发生的次数。常用于预估电子产品寿命，页面请求间的时间间隔。 print(rng.exponential(scale=1.0, size=3)) # [0.48583027, 1.45895053, 1.30734696] print('某产品平均10年发生一次重大故障，要求保修的比例不超过20%，请问应设几年质保？过10年后，约有多少产品发生重大故障？') la = 1/10 # 发生概率 print('{:.2f}年'.format(stats.expon.ppf(0.2, scale=1/la))) print('{:.2f}%的产品发生重大故障'.format(stats.expon.cdf(10, scale=1/la)*100)) # 某产品平均10年发生一次重大故障，要求保修的比例不超过20%，请问应设几年质保？过10年后，约有多少产品发生重大故障？ # 2.23年

# 63.21%的产品发生重大故障 F分布分布 f(dfnum, dfden, size=None) dfnum分子自由度，dfden分母自由度。 F分布是一种非对称连续概率分布，有两个自由度，且位置不可互换。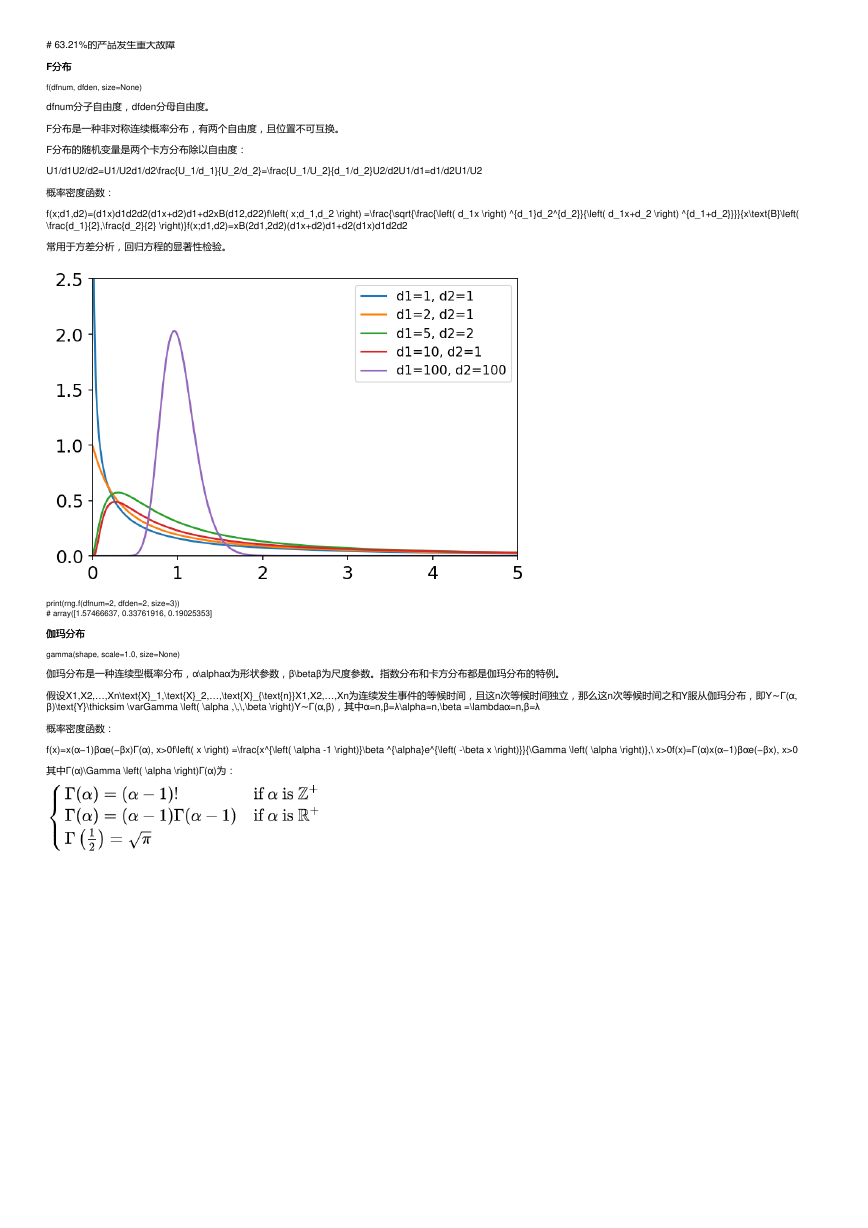 F分布的随机变量是两个卡方分布除以自由度： U1/d1U2/d2=U1/U2d1/d2\frac{U_1/d_1}{U_2/d_2}=\frac{U_1/U_2}{d_1/d_2}U2/d2U1/d1 =d1/d2U1/U2 概率密度函数： f(x;d1,d2)=(d1x)d1d2d2(d1x+d2)d1+d2xB(d12,d22)f\left( x;d_1,d_2 \right) =\frac{\sqrt{\frac{\left( d_1x \right) ^{d_1}d_2^{d_2}}{\left( d_1x+d_2 \right) ^{d_1+d_2}}}}{x\text{B}\left( \frac{d_1}{2},\frac{d_2}{2} \right)}f(x;d1,d2)=xB(2d1 )(d1x+d2)d1+d2(d1x)d1d2d2 ,2d2 常用于方差分析，回归方程的显著性检验。 print(rng.f(dfnum=2, dfden=2, size=3)) # array([1.57466637, 0.33761916, 0.19025353] 伽玛分布伽玛分布 gamma(shape, scale=1.0, size=None) 伽玛分布是一种连续型概率分布，α\alphaα为形状参数，β\betaβ为尺度参数。指数分布和卡方分布都是伽玛分布的特例。假设X1,X2,…,Xn\text{X}_1,\text{X}_2,…,\text{X}_{\text{n}}X1,X2,…,Xn为连续发生事件的等候时间，且这n次等候时间独立，那么这n次等候时间之和Y服从伽玛分布，即Y∼Γ(α, β)\text{Y}\thicksim \varGamma \left( \alpha ,\,\,\beta \right)Y∼Γ(α,β)，其中α=n,β=λ\alpha=n,\beta =\lambdaα=n,β=λ 概率密度函数： f(x)=x(α−1)βαe(−βx)Γ(α), x>0f\left( x \right) =\frac{x^{\left( \alpha -1 \right)}\beta ^{\alpha}e^{\left( -\beta x \right)}}{\Gamma \left( \alpha \right)},\ x>0f(x)=Γ(α)x(α−1)βαe(−βx), x>0 其中Γ(α)\Gamma \left( \alpha \right)Γ(α)为：

print(rng.gamma(shape=2, scale=2, size=3)) # shape即alpha，scale即beta # [4.34964442, 6.21444278, 4.25584051] 几何分布几何分布 geometric(p, size=None) 几何分布是一种离散型概率分布。在n次伯努利试验中，前k-1次都失败，第k次成功的概率。如不停地掷骰子直到掷到1是一个p=1/6的几何分布。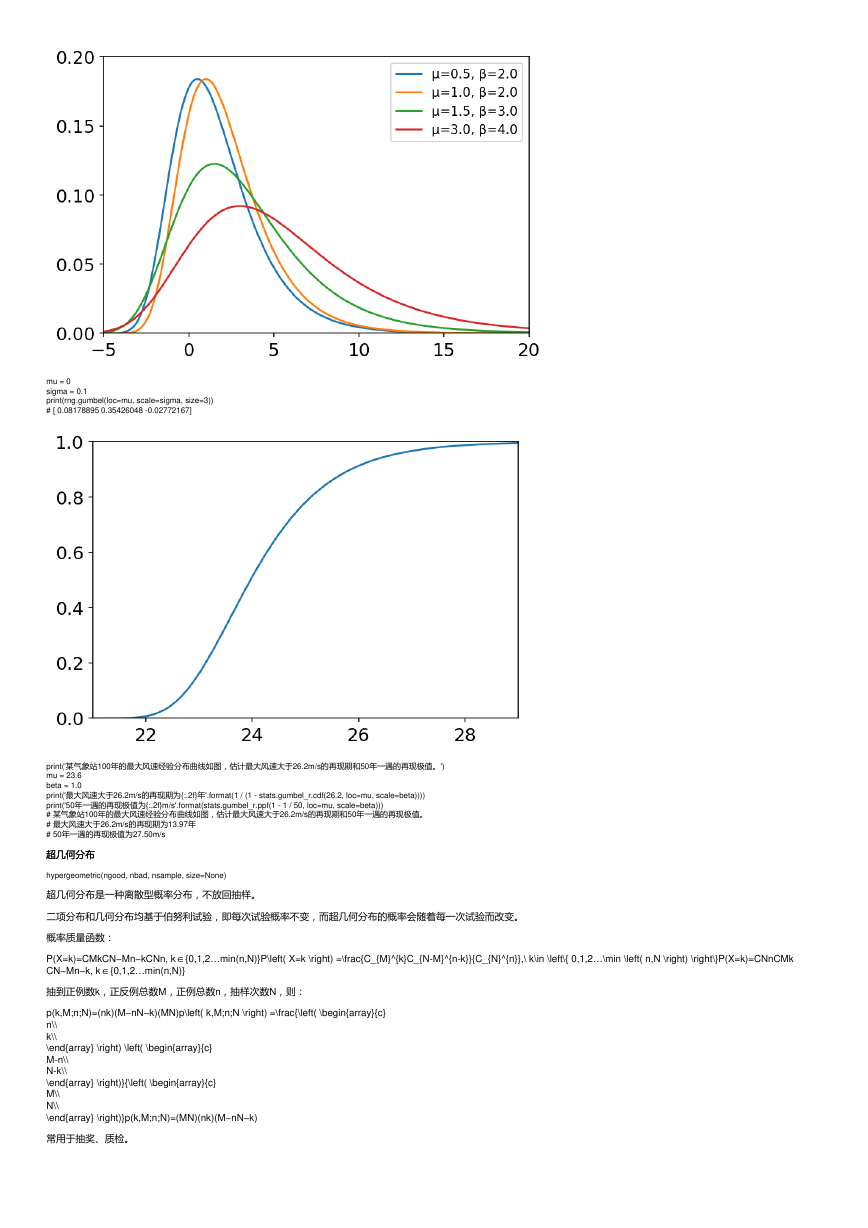概率质量函数： f(x)=(1−p)x−1p, x=1,2,…f\left( x \right) =\left( 1-p \right) ^{x-1}p,\ x=1,2,…f(x)=(1−p)x−1p, x=1,2,… print(rng.geometric(p=0.2, size=10)) # [ 4 1 7 1 14 5 1 5 3 7] 耿贝尔分布耿贝尔分布 gumbel(loc=0.0, scale=1.0, size=None) 耿贝尔分布是一种连续型概率分布，模拟不同分布的最大值(或最小值)的分布。μ\muμ为中心参数，β\betaβ为展宽参数。概率密度函数： f(x)=1βe−(z+e−z)f\left( x \right) =\frac{1}{\beta}e^{-\left( z+e^{-z} \right)}f(x)=β1e−(z+e−z) 其中z=x−μβz=\frac{x-\mu}{\beta}z=βx−μ 常用于多年一遇事件，最大风速计算，极端潮位，预测地震洪水或其他自然灾害发生的几率等。

mu = 0 sigma = 0.1 print(rng.gumbel(loc=mu, scale=sigma, size=3)) # [ 0.08178895 0.35426048 -0.02772167] print('某气象站100年的最大风速经验分布曲线如图，估计最大风速大于26.2m/s的再现期和50年一遇的再现极值。') mu = 23.6 beta = 1.0 print('最大风速大于26.2m/s的再现期为{:.2f}年'.format(1 / (1 - stats.gumbel_r.cdf(26.2, loc=mu, scale=beta)))) print('50年一遇的再现极值为{:.2f}m/s'.format(stats.gumbel_r.ppf(1 - 1 / 50, loc=mu, scale=beta))) # 某气象站100年的最大风速经验分布曲线如图，估计最大风速大于26.2m/s的再现期和50年一遇的再现极值。 # 最大风速大于26.2m/s的再现期为13.97年 # 50年一遇的再现极值为27.50m/s 超几何分布超几何分布 hypergeometric(ngood, nbad, nsample, size=None) 超几何分布是一种离散型概率分布，不放回抽样。二项分布和几何分布均基于伯努利试验，即每次试验概率不变，而超几何分布的概率会随着每一次试验而改变。概率质量函数： P(X=k)=CMkCN−Mn−kCNn, k∈{0,1,2…min⁡(n,N)}P\left( X=k \right) =\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}},\ k\in \left\{ 0,1,2…\min \left( n,N \right) \right\}P(X=k)=CNnCMk CN−Mn−k , k∈{0,1,2…min(n,N)} 抽到正例数k，正反例总数M，正例总数n，抽样次数N，则： p(k,M;n;N)=(nk)(M−nN−k)(MN)p\left( k,M;n;N \right) =\frac{\left( \begin{array}{c} n\\ k\\ \end{array} \right) \left( \begin{array}{c} M-n\\ N-k\\ \end{array} \right)}{\left( \begin{array}{c} M\\ N\\ \end{array} \right)}p(k,M;n;N)=(MN)(nk)(M−nN−k) 常用于抽奖、质检。

资料库

Python概率分布大全（含可视化）.pdf

相关推荐

开发技术

热门标签

最新资料