logo资料库

负荷频率控制系统的线性自抗扰控制.pdf

发布时间：2022-06-06 发布人：admin 分类：说明书 资料大小：5.41M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    第 30 卷第 12 期 2013 年 12 月 DOI: 10.7641/CTA.2013.30979 控 制 理 论 与 应 用 Control Theory & Applications Vol. 30 No. 12 Dec. 2013 负负负荷荷荷频频频率率率控控控制制制系系系统统统的的的线线线性性性自自自抗抗抗扰扰扰控控控制制制 谭 文†, 周 宏, 傅彩芬 (华北电力大学 控制与计算机工程学院, 北京 102206) 摘要: 本文研究负荷频率控制系统的线性自抗扰控制(linear active disturbance rejection, LADRC)方法. 考虑负荷 频率控制系统的模型及结构, 本文首先通过一仿真例子分析了二阶和三阶LADRC在单区域电力系统的控制性能, 指出二阶LADRC在负荷频率控制中的限制. 随后本文针对负荷频率控制中存在的发电速率约束(generation rate constraint, GRC)这一实际问题, 提出一种anti-GRC补偿方案. 该方案将汽轮机理论输出与实际输出误差作为扰动输 入, 利用扩张状态观测器进行估计, 从而使LADRC能够快速补偿该误差, 达到抗积分饱和的作用. 最后, 本文将 LADRC设计方法推广到具有再热汽轮机和水轮机系统以及多区域电力系统. 仿真表明LADRC是一种独立于模型 的普适性控制结构, 所需整定参数少, 能够取得比PID控制更好的抗干扰性能, 可以应用到负荷频率控制系统中. 关键词: 线性自抗扰控制; 负荷频率控制; 电力系统; PID控制 中图分类号: TP273 文献标识码: A Linear active disturbance rejection control for load frequency control of power systems TAN Wen†, ZHOU Hong, FU Cai-fen (School of Control & Computer Engineering, North China Electric Power University, Beijing 102206, China) Abstract: We apply the linear active disturbance rejection approach (LADRC) to the load-frequency control (LFC) of power systems. Considering the model and the structure of the controlled system, we analyze a second order and a third order LADRCs for a single-area power system with non-reheated turbine; and reveal the limitations of the 2nd-order LADRC. To deal with the generation rate constraint (GRC) of the system, we propose an anti-GRC scheme for LADRC, where the error between the computed output and the real output of the turbine is fed back to the extended state observer for fast compensation of the windup. Finally, the LADRC is extended to power systems with reheated and hydro-turbines, and multi-area power systems. It is found that LADRC is a model-free control method with only two tuning parameters. Thus, it is very practical in industrial control. Simulation examples show that LADRC can reduce the load disturbance very well and is readily applicable to the load-frequency control system. Key words: active disturbance rejection control; load frequency control; power systems; PID control 1 引引引言言言(Introduction) 频率稳定是电力系统电能质量的一个重要指标. 负荷的任意突然变化都有可能导致系统间联络线交 换功率的偏差及系统频率的波动. 因此, 为保证电能 质量, 需要一个负荷频率控制(load frequency control, LFC)系统, 该系统的目的是将系统频率维持在标称值 并且尽可能使控制区域之间的未计划的联络线交换 功率最小[1]. 常规LFC仅使用积分控制. 熟知较大的积分增益 会恶化系统性能, 导致较大系统振荡, 甚至不稳定. 因 此积分增益的设置必须在系统理想的暂态恢复响应 和较小的超调之间进行折中. 目前文献中报道了许多 整定LFC积分增益的方法[2]. 随着现代电力系统的规模和复杂程度逐渐增大, 系统振荡更有可能在系统中扩大而导致停电, 因此先 进 控 制 算 法 在LFC中 得 到 广 泛 研 究, 包 括 最 优 控 制[3–4]、变结构控制[5]、自适应控制[6], 以及鲁棒控 制[7–9]等. 先进控制方法确实可以提高系统性能, 但是 这些方法或者需要系统全部状态信息, 或者需要有效 的在线辨识, 在实际中难以实现. 同时, 不少文献提出通过扩展常规PI控制的方法 来达到有效抑制电力系统频率振荡的方法. 负荷频率 控制中采用PID 控制的困难之处在于电力系统模型是 高阶欠阻尼的, 而现有大多数PID整定方法都侧重于 收稿日期: 2013−09−17; 收修改稿日期: 2013−11−06. †通信作者. E-mail: wtan@ncepu.edu.cn; Tel.: +86 10-61772107. 基金项目: 国家自然科学基金资助项目(61174096); 北京市自然科学基金资助项目(4122075); 河北省自然科学基金资助项目(F2011502069).
    第 12 期 谭文等: 负荷频率控制系统的线性自抗扰控制 1581 过阻尼过程, 因此在LFC中直接采用现有PID方法整 定不合适. 为此, 文献[10–11]提出一种基于两自由度 内模控制的PID整定方法, 该方法只需整定2个参数， 并且可以取得较好的振荡抑制效果. 文献[12]将线性自抗扰控制(LADRC)方法应用到 负荷频率控制问题. 该方法通过一个扩张观测器估计 系统的扰动, 从而达到更快抑制扰动的目的, 而且该 方案只需调节2个参数, 因此可以很容易为现场工程 师 掌 握. 本 文 将 在 文 献[12]的 基 础 上 进 一 步 分 析 LADRC方法在负荷频率控制中的应用, 重点在于解 决如下两个问题: 1) 负荷频率控制中如何选取适当的LADRC阶数 以及相应的参数? 2) 当系统存在发电速率约束(GRC)时, 如何避免 控制器饱和? 研究表明: LADRC能取得较好的振荡抑制性能, 而且参数整定简单, 能够应用于负荷频率控制系统. 2 负负负荷荷荷频频频率率率控控控制制制系系系统统统模模模型型型(System model for LFC) 考虑图1所示的单区域负荷频率控制系统(在某个 操作点附近线性化模型)[13]. 图 1 单区域电力系统 Fig. 1 Single-area power system 图中 1 R 为机组下降特性, 而 1 ; 1 1) Gg(s)为调节阀动态: Gg(s) = TGs + 1 2) Gt(s)为汽轮机动态: Gt(s) = ; 3) Gp(s)为负荷及电机动态: Gp(s) = KP 因此, 系统开环传递函数可表示如下: ∆f = G(s)u − Gd(s)∆Pd, TTs + 1 . TPs + 1 (1) 其中: G(s) = Gp(s)Gt(s)Gg(s) 1 + Gp(s)Gt(s)Gg(s)/R , Gd(s) = Gp(s) 1 + Gp(s)Gt(s)Gg(s)/R . 可以看到, 负荷频率控制问题是一个扰动抑制问题: 采用反馈u=−K(s)∆f 镇定对象G(s)并且使得∆Pd 对频率变化∆f 的影响最小. 3 线线线性性性自自自抗抗抗扰扰扰控控控制制制(LADRC) 自 抗 扰 控 制(active disturbance rejection control, ADRC)由中科院韩京清教授提出[14], 其思想是采用 一个扩张状态观测器(ESO)来估计系统的扰动, 然后 使用简单控制进行抑制. 该思想类似于反馈线性化, 但是在结构上更简单且适应于各种非线性系统. 非线 性ADRC需要调节多个参数, 因此在实际应用中受到 限制. 为了克服这个困难, 文献[15]考虑了ADRC的 “线性”版本. 线性自抗扰控制最终只需调节2个参 数, 从而大大简化了ADRC的整定过程, 并且可以利 用经典控制方法分析闭环系统的稳定性及频率响应, 使得其在工业中应用得到可能. 3.1 结结结构构构(Structure of LADRC) 考虑如下线性系统: Y (s) = G(s)U(s) + Gd(s)D(s), (2) 其中: G(s) = Gd(s) = bmsm + ··· + b1s + b0 ansn + an−1sn−1 + ··· + a1s + a0 , chsh + ··· + c1s + c0 ansn + an−1sn−1 + ··· + a1s + a0 或者写成微分方程形式 any(n)(t) + an−1y(n−1)(t) + ··· + a1 ˙y(t) + a0y(t) = bmu(m)(t) + ··· + b1 ˙u(t) + b0u(t) + chd(h)(t) + ··· + c1 ˙d(t) + c0d(t), , (3) 其中: y(t), u(t)和d(t)分别是系统输出、输入和扰动; Y (s), U(s)和D(s) 为其 Laplace 变换. G(s) 和 Gd(s) 分别是被控对象和外部扰动的传递函数. 自抗扰控制不需要知道被控对象和扰动的完全模 型, 只需知道对象相对阶r := n − m以及增益b := bm/an. 也就是说, 被控系统假设具有如下模型: y(r)(t) = bu(t) + f(y(t), u(t), d(t)), (4) 其中f(y, u, d)是系统未知动态以及外部扰动的组合, 在ADRC设计中假设为未知的, 称为广义扰动. ADRC方法基本思想是利用一个扩张状态观测器 来估计未知的广义扰动. 令 z1 = y, z2 = ˙y, zr+1 = f(y, u, d). ··· , zr = y(r−1), 设f(y, u, d)可微分且 ˙f(y, u, d) = h(t). 则系统模型 (4)可写成  ˙z = Aoz + Bou + Eoh, y = Coz, (5) (6)
    1582 控 制 理 论 与 应 用 (r+1)×(r+1) Ao = ... ... ...     其中: z = [z1 z2 ··· zr zr+1]T, 0 1 0 ··· 0 0 0 1 ··· 0 ... ... 0 0 0 ··· 1 0 0 0 ··· 0 0 0 ... b 0 0 0 ... 0 1 Co = [1 0 0 ··· 0]1×(r+1).   , Eo = (r+1)×1 Bo =  对该系统设计全阶Luenberger观测器: ˙ˆz = Aoˆz + Bou + Lo(y − ˆy), ˆy = Coˆz, 其中Lo为观测器增益: , (7) , (r+1)×1 Lo = [β1 β2 ··· βr βr+1]T. (9) 当Ao − LoCo渐近稳定时, ˆz1(t),··· , ˆzr(t)趋近于输 出y(t)及其各阶导数(直至r阶), 并且ˆzr+1(t)趋近于广 义扰动f(y, u, d). 这意味着可以利用这个扰动估计进 行控制, 从而使其得到更快地抑制. 取如下控制率: u(t) = −ˆzr+1(t) + uo(t) b , (10) 其中uo(t)待定. 此时被控系统(4)变为 y(r)(t) = f(y, u, d) − ˆzr+1(t) + uo(t). (11) 当ESO设计适当时, 即有ˆzr+1 ≈ f(y, u, d), 从而系统 变成一个r重积分系统 y(r)(t) ≈ uo(t). (12) 该系统可以采用如下状态反馈控制率控制: uo(t)=−k1y(t) − k2 ˙y(t) − ··· − kry(r−1)(t), (13) 因为ˆz1(t),··· , ˆzr(t)趋近y(t),··· , y(r−1)(t), 因此最 终控制率可以逼近为 u(t)=− k1ˆz1(t)+···+kr ˆzr(t)+ˆzr+1(t) b =−Koˆz, (14) 其中 Ko = [k1 k2 ··· kr 1]/b. (15) 3.2 参参参数数数整整整定定定(Parameter tuning for LADRC) 可以看到, 一个线性自抗扰控制需要设计两组参 数: ESO观测器增益Lo以及r重积分系统的状态反馈 第 30 卷 控制增益Ko. 为方便, 文献[15] 提出将这两组增益的 整定转化为两个参数的整定: 即控制器带宽ωc及观测 器带宽ωo. 考虑ESO, Ao − LoCo的特征方程为 |sI − (Ao − LoCo)| = sr+1 + β1sr + ··· + βr+1. (16) 为简便, 假设所有观测器极点配置在−ωo, 即 sr+1 + β1sr + ··· + βr+1 = (s + ωo)r+1, 从而 其中 r + 1 i βi = r + 1 i o, i = 1,··· , r + 1, ωi (17) (18) 为组合系数. 于是观测器增益只需调节 单个参数ωo. (8) 当广义扰动f(y, u, d)可以准确估计时, 原系统变 成一个多重积分模型, 且当ˆzi(i = 1,··· , r)也近似对 象输出及其导数时, 状态反馈闭环特征方程为 |sI − (Ao − BoKo)| = s(sr + knsr−1 + ··· + k2s + k1). (19) 可以看到该控制在原点处存在一个零点因此该控制 总是包含积分控制从而可以消除稳态误差. 类似地, 为简便可以将所有控制器极点(除原点外)配置在−ωc, 即 sr + krsr−1 + ··· + k2s + k1 = (s + ωc)r, 于是 ki = r i − 1 ωn−i+1 c , i = 1,··· , r, (20) (21) (22) 线性自抗扰控制器具有如下状态空间实现: 从而反馈控制率增益只需调节单个参数ωc. 3.3 小小小结结结(Summary)  ˙ˆz = Aoˆz + Bou + Lo(y − Coˆz) = (Ao − BoKo − LoCo)ˆz + Loy, u = −Koˆz, 或者传递函数形式 u(s)=−Ko(sI−Ao+BoKo+LoCo)−1Loy(s). (23) 可以看到LADRC是一种独立于被控对象模型的 普适性控制结构. 除了需要知道对象的相对阶r及相 应增益b, 无需知道模型的具体结构和参数. 这与PID 控制很相似, 具有独立于模型的固定控制结构. 特别 地, LADRC只需整定2个参数, 因此很容易为控制工 程师理解. 该结构本身自带积分行为, 因此设计中无 需再额外加入积分器.
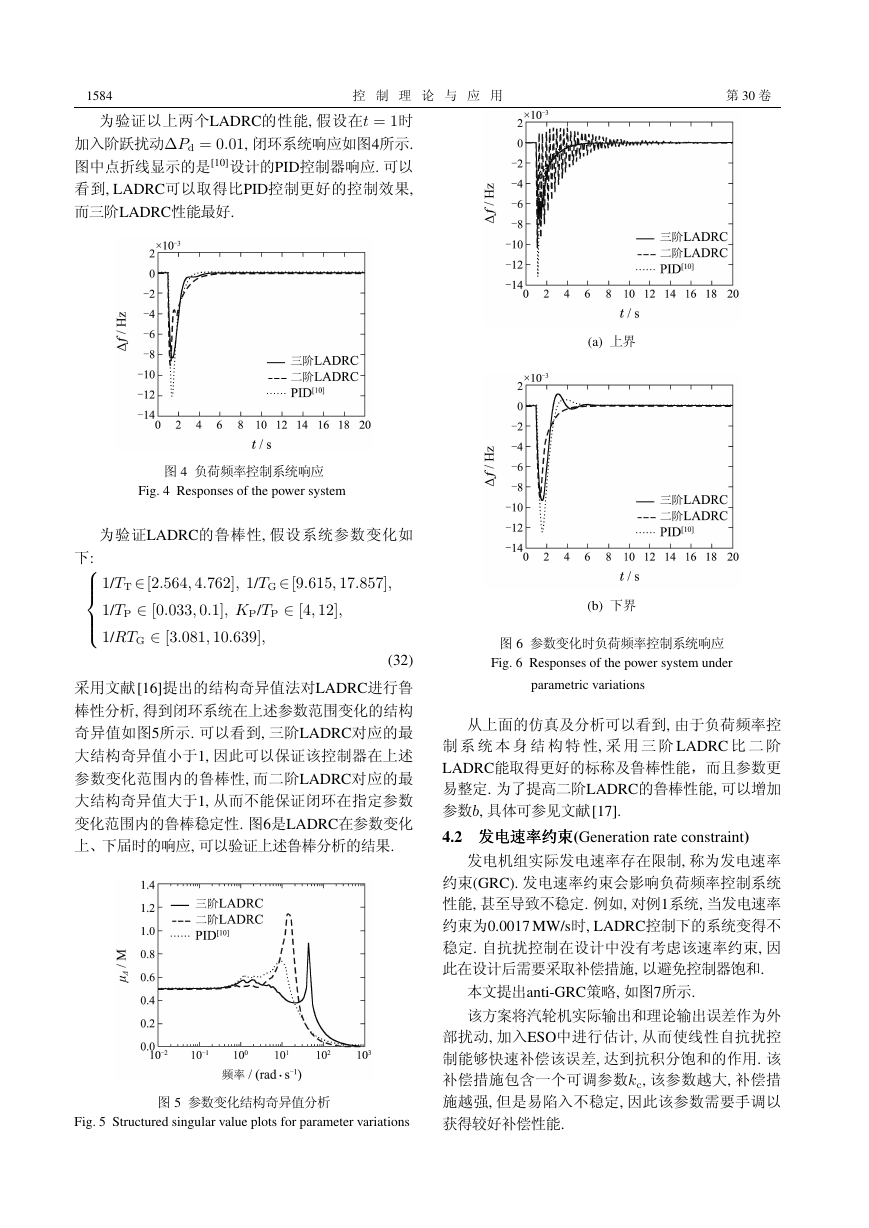
    第 12 期 4 负负负荷荷荷频频频率率率控控控制制制系系系 统统统 的的的 线线线 性性性 自自自 抗抗抗 扰扰扰 控控控 制制制 谭文等: 负荷频率控制系统的线性自抗扰控制 1583 (LADRC for LFC) 根据负荷频率控制系统模型(1), 可以求得LFC系 统的开环传递函数, 然后采用上节所述方法进行线性 自抗扰控制设计. 针对负荷频率控制系统, 存在两个 重要问题, 以下分别进行讨论. 4.1 线线线性性性自自自抗抗抗扰扰扰控控控制制制的的的阶阶阶数数数(Order of LADRC) 设计LADRC的首要步骤是确定其阶数. 对于具有 非再热汽轮机的机组, 其开环传递函数为 G(s)= KP (TPs+1)(TTs+1)(TGs+1)+KP/R , (24) (b) 三阶LADRC 其相对阶为3, 因此可以采用三阶LADRC进行控制, 并且简化后的多重积分对象增益为 b = KP TpTTTG . (25) 注意到负荷频率控制系统可以近似为二阶模型[10] Gr(s) = kω2 n s2 + 2ζωns + ω2 n e−τ s. (26) 因此一个问题是负荷频率控制系统能否采用更低价 的LADRC来控制? 以下将用一个典型单区域电力系 统来说明二阶自抗扰控制在负荷频率控制中的限制. 例例例 1 考虑具有如下模型参数的电力系统: KP =120, TP =20, TT =0.3, TG =0.08, R=2.4, (27) 易得开环传递函数为 G(s) = 250 s3 + 15.88s2 + 42.46s + 106.3 , (28) 而其二阶近似模型为[10] Gr(s) = 18.824 s2 + 2.64s + 8 e−0.0757s. (29) 对该系统分别设计三阶及二阶线性自抗扰控制器. 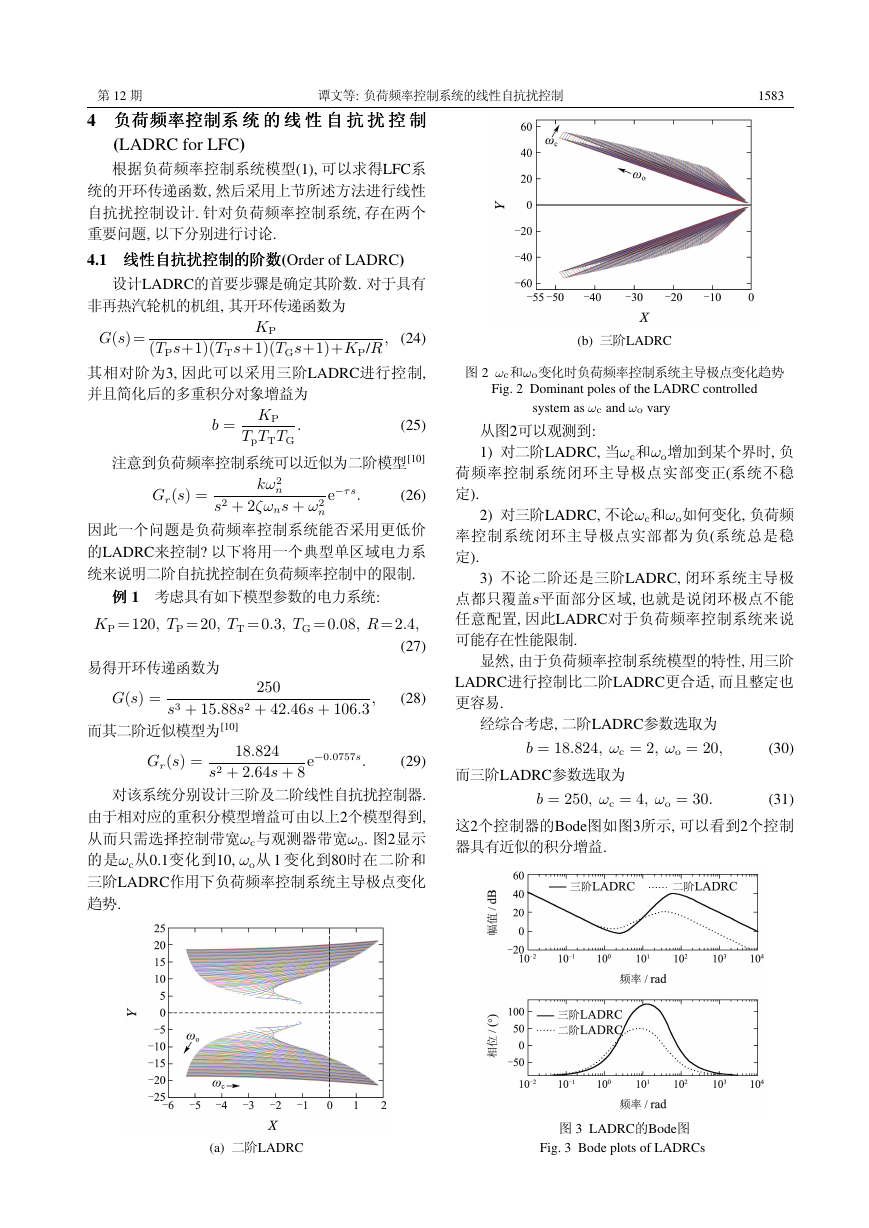由于相对应的重积分模型增益可由以上2个模型得到, 从而只需选择控制带宽ωc与观测器带宽ωo. 图2显示 的是ωc从0.1变化到10, ωo从 1 变化到80时在二阶和 三阶LADRC作用下负荷频率控制系统主导极点变化 趋势. 图 2 ωc和ωo变化时负荷频率控制系统主导极点变化趋势 Fig. 2 Dominant poles of the LADRC controlled system as ωc and ωo vary 从图2可以观测到: 1) 对二阶LADRC, 当ωc和ωo增加到某个界时, 负 荷频率控制系统闭环主导极点实部变正(系统不稳 定). 2) 对三阶LADRC, 不论ωc和ωo如何变化, 负荷频 率控制系统闭环主导极点实部都为负(系统总是稳 定). 3) 不论二阶还是三阶LADRC, 闭环系统主导极 点都只覆盖s平面部分区域, 也就是说闭环极点不能 任意配置, 因此LADRC对于负荷频率控制系统来说 可能存在性能限制. 显然, 由于负荷频率控制系统模型的特性, 用三阶 LADRC进行控制比二阶LADRC更合适, 而且整定也 更容易. 经综合考虑, 二阶LADRC参数选取为 b = 18.824, ωc = 2, ωo = 20, (30) 而三阶LADRC参数选取为 b = 250, ωc = 4, ωo = 30. 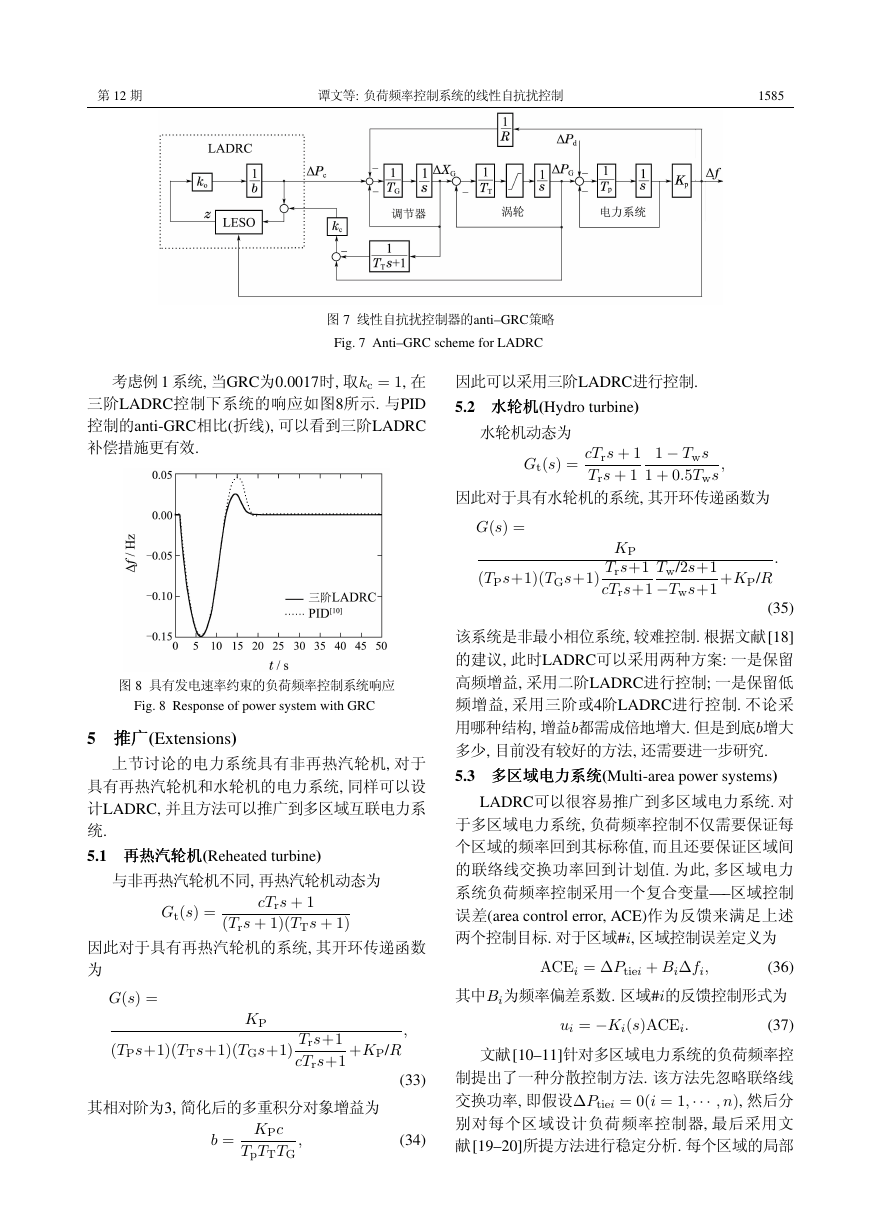(31) 这2个控制器的Bode图如图3所示, 可以看到2个控制 器具有近似的积分增益. (a) 二阶LADRC 图 3 LADRC的Bode图 Fig. 3 Bode plots of LADRCs
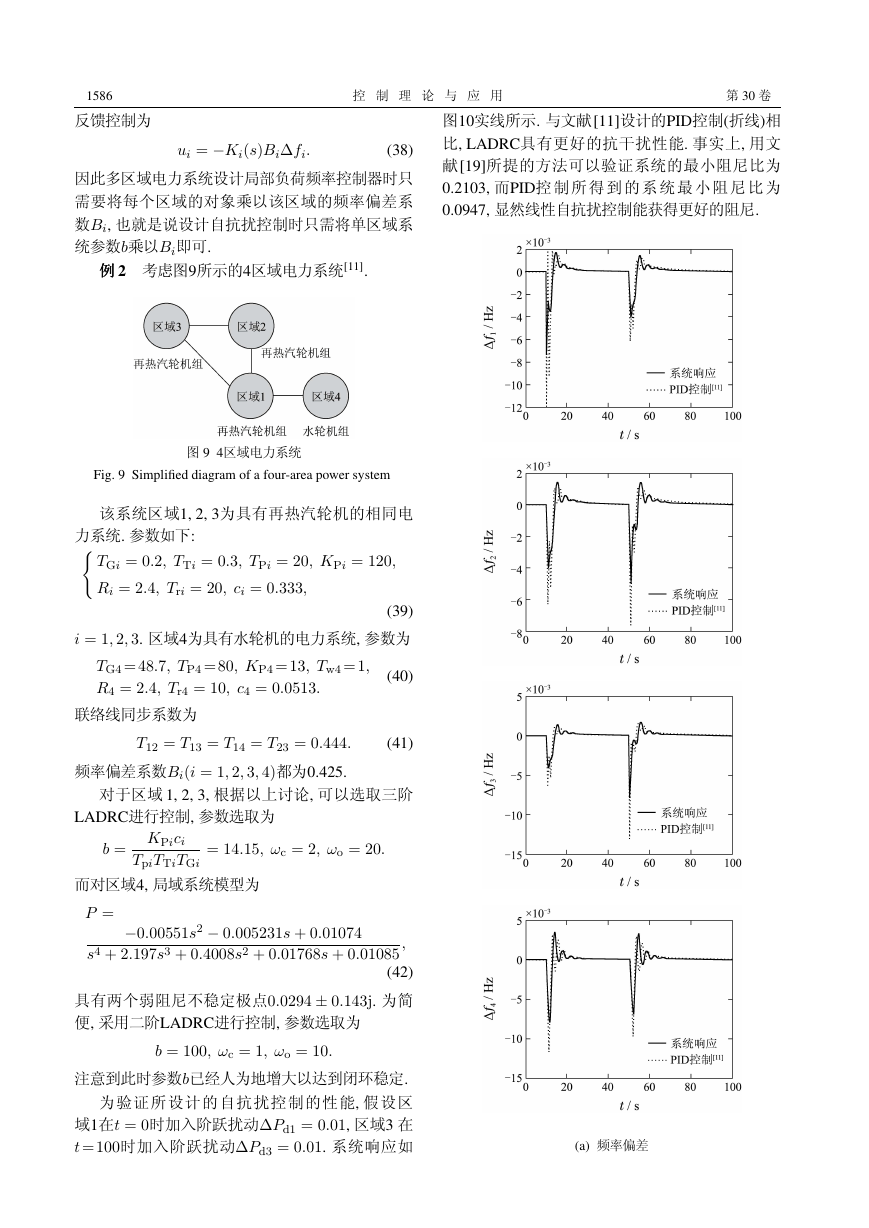
    1584 控 制 理 论 与 应 用 第 30 卷 为验证以上两个LADRC的性能, 假设在t = 1时 加入阶跃扰动∆Pd = 0.01, 闭环系统响应如图4所示. 图中点折线显示的是[10]设计的PID控制器响应. 可以 看到, LADRC可以取得比PID控制更好的控制效果, 而三阶LADRC性能最好. (a) 上界 图 4 负荷频率控制系统响应 Fig. 4 Responses of the power system 为验证LADRC的鲁棒性, 假设系统参数变化如 下: 1/TT∈[2.564, 4.762], 1/TG∈[9.615, 17.857], 1/TP ∈ [0.033, 0.1], KP/TP ∈ [4, 12], 1/RTG ∈ [3.081, 10.639], (32) 采用文献[16]提出的结构奇异值法对LADRC进行鲁 棒性分析, 得到闭环系统在上述参数范围变化的结构 奇异值如图5所示. 可以看到, 三阶LADRC对应的最 大结构奇异值小于1, 因此可以保证该控制器在上述 参数变化范围内的鲁棒性, 而二阶LADRC对应的最 大结构奇异值大于1, 从而不能保证闭环在指定参数 变化范围内的鲁棒稳定性. 图6是LADRC在参数变化 上、下届时的响应, 可以验证上述鲁棒分析的结果. 图 5 参数变化结构奇异值分析 Fig. 5 Structured singular value plots for parameter variations (b) 下界 图 6 参数变化时负荷频率控制系统响应 Fig. 6 Responses of the power system under parametric variations 从上面的仿真及分析可以看到, 由于负荷频率控 制 系 统 本 身 结 构 特 性, 采 用 三 阶 LADRC 比 二 阶 LADRC能取得更好的标称及鲁棒性能，而且参数更 易整定. 为了提高二阶LADRC的鲁棒性能, 可以增加 参数b, 具体可参见文献[17]. 4.2 发发发电电电速速速率率率约约约束束束(Generation rate constraint) 发电机组实际发电速率存在限制, 称为发电速率 约束(GRC). 发电速率约束会影响负荷频率控制系统 性能, 甚至导致不稳定. 例如, 对例1系统, 当发电速率 约束为0.0017 MW/s时, LADRC控制下的系统变得不 稳定. 自抗扰控制在设计中没有考虑该速率约束, 因 此在设计后需要采取补偿措施, 以避免控制器饱和. 本文提出anti-GRC策略, 如图7所示. 该方案将汽轮机实际输出和理论输出误差作为外 部扰动, 加入ESO中进行估计, 从而使线性自抗扰控 制能够快速补偿该误差, 达到抗积分饱和的作用. 该 补偿措施包含一个可调参数kc, 该参数越大, 补偿措 施越强, 但是易陷入不稳定, 因此该参数需要手调以 获得较好补偿性能.
    第 12 期 谭文等: 负荷频率控制系统的线性自抗扰控制 1585 图 7 线性自抗扰控制器的anti–GRC策略 Fig. 7 Anti–GRC scheme for LADRC 考虑例 1 系统, 当GRC为0.0017时, 取kc = 1, 在 三阶LADRC控制下系统的响应如图8所示. 与PID 控制的anti-GRC相比(折线), 可以看到三阶LADRC 补偿措施更有效. 图 8 具有发电速率约束的负荷频率控制系统响应 Fig. 8 Response of power system with GRC 5 推推推广广广(Extensions) 上节讨论的电力系统具有非再热汽轮机, 对于 具有再热汽轮机和水轮机的电力系统, 同样可以设 计LADRC, 并且方法可以推广到多区域互联电力系 统. 5.1 再再再热热热汽汽汽轮轮轮机机机(Reheated turbine) 与非再热汽轮机不同, 再热汽轮机动态为 Gt(s) = cTrs + 1 (Trs + 1)(TTs + 1) 因此对于具有再热汽轮机的系统, 其开环传递函数 为 G(s) = KP (TPs+1)(TTs+1)(TGs+1) Trs+1 cTrs+1 , +KP/R 其相对阶为3, 简化后的多重积分对象增益为 b = KPc TpTTTG , (33) (34) 因此可以采用三阶LADRC进行控制. 5.2 水水水轮轮轮机机机(Hydro turbine) 水轮机动态为 Gt(s) = cTrs + 1 Trs + 1 1 − Tws 1 + 0.5Tws , 因此对于具有水轮机的系统, 其开环传递函数为 G(s) = KP (TPs+1)(TGs+1) Trs+1 cTrs+1 Tw/2s+1 −Tws+1 . +KP/R (35) 该系统是非最小相位系统, 较难控制. 根据文献[18] 的建议, 此时LADRC可以采用两种方案: 一是保留 高频增益, 采用二阶LADRC进行控制; 一是保留低 频增益, 采用三阶或4阶LADRC进行控制. 不论采 用哪种结构, 增益b都需成倍地增大. 但是到底b增大 多少, 目前没有较好的方法, 还需要进一步研究. 5.3 多多多区区区域域域电电电力力力系系系统统统(Multi-area power systems) LADRC可以很容易推广到多区域电力系统. 对 于多区域电力系统, 负荷频率控制不仅需要保证每 个区域的频率回到其标称值, 而且还要保证区域间 的联络线交换功率回到计划值. 为此, 多区域电力 系统负荷频率控制采用一个复合变量—–区域控制 误差(area control error, ACE)作为反馈来满足上述 两个控制目标. 对于区域#i, 区域控制误差定义为 ACEi = ∆Ptiei + Bi∆fi, (36) 其中Bi为频率偏差系数. 区域#i的反馈控制形式为 (37) ui = −Ki(s)ACEi. 文献[10–11]针对多区域电力系统的负荷频率控 制提出了一种分散控制方法. 该方法先忽略联络线 交换功率, 即假设∆Ptiei = 0(i = 1,··· , n), 然后分 别对每个区域设计负荷频率控制器, 最后采用文 献[19–20]所提方法进行稳定分析. 每个区域的局部
    控 制 理 论 与 应 用 第 30 卷 图10实线所示. 与文献[11]设计的PID控制(折线)相 比, LADRC具有更好的抗干扰性能. 事实上, 用文 献[19]所提的方法可以验证系统的最小阻尼比为 0.2103, 而PID控 制 所 得 到 的 系 统 最 小 阻 尼 比 为 0.0947, 显然线性自抗扰控制能获得更好的阻尼. 1586 反馈控制为 ui = −Ki(s)Bi∆fi. (38) 因此多区域电力系统设计局部负荷频率控制器时只 需要将每个区域的对象乘以该区域的频率偏差系 数Bi, 也就是说设计自抗扰控制时只需将单区域系 统参数b乘以Bi即可. 例例例 2 考虑图9所示的4区域电力系统[11]. 图 9 4区域电力系统 Fig. 9 Simplified diagram of a four-area power system 该系统区域1, 2, 3为具有再热汽轮机的相同电 力系统. 参数如下: TGi = 0.2, TTi = 0.3, TPi = 20, KPi = 120, Ri = 2.4, Tri = 20, ci = 0.333, (39) i = 1, 2, 3. 区域4为具有水轮机的电力系统, 参数为 TG4 =48.7, TP4 =80, KP4 =13, Tw4 =1, R4 = 2.4, Tr4 = 10, c4 = 0.0513. 联络线同步系数为 T12 = T13 = T14 = T23 = 0.444. 频率偏差系数Bi(i = 1, 2, 3, 4)都为0.425. (40) (41) 对于区域 1, 2, 3, 根据以上讨论, 可以选取三阶 LADRC进行控制, 参数选取为 b = KPici TpiTTiTGi = 14.15, ωc = 2, ωo = 20. 而对区域4, 局域系统模型为 P = −0.00551s2 − 0.005231s + 0.01074 s4 + 2.197s3 + 0.4008s2 + 0.01768s + 0.01085 , (42) 具有两个弱阻尼不稳定极点0.0294 ± 0.143j. 为简 便, 采用二阶LADRC进行控制, 参数选取为 b = 100, ωc = 1, ωo = 10. 注意到此时参数b已经人为地增大以达到闭环稳定. 为验证所设计的自抗扰控制的性能, 假设区 域1在t = 0时加入阶跃扰动∆Pd1 = 0.01, 区域3 在 t=100时加入阶跃扰动∆Pd3 = 0.01. 系统响应如 (a) 频率偏差
    第 12 期 谭文等: 负荷频率控制系统的线性自抗扰控制 1587 6 结结结论论论(Conclusion) 本文研究了负荷频率控制系统的线性自抗扰控 制方法. 首先分析了二阶和三阶LADRC在单区域 电力系统的控制性能, 指出二阶LADRC在负荷频 率控制中存在的限制. 随后本文针对负荷频率控制 中存在的发电速率约束这一实际问题, 提出一种 anti-GRC补偿方案. 最后, 本文将LADRC设计方法 推广到再热汽轮机和水轮机系统以及多区域电力系 统. 仿真表明LADRC是一种独立于模型的普适性 控制结构, 所需整定参数少, 能够取得比PID控制更 好的抗干扰性能. 由于LADRC在控制非最小相位 系统时存在一些限制, 因此对于具有水轮机的电力 系统, 其线性自抗扰控制的设计还需进一步研究. 参参参考考考文文文献献献(References): [1] TAN W. Load frequency control: problems and solutions [C] //Pro- IEEE, ceedings of the 30th Chinese Control Conference. Yantai: 2011: 6281 – 6286. [2] SAADAT H. Power System Analysis [M]. New York: McGraw-Hill, 1999. [3] FOSHA C E, ELGERD O I. The megawatt-frequency control prob- lem: a new approach via optimal control theory [J]. IEEE Transac- tions on Power Apparatus and Systems, 1970, 89(4): 563 – 567. [4] CALOVIC M. Linear regulator design for a load and frequency con- trol theory [J]. IEEE Transactions on Power Apparatus and Systems, 1972, 91(6): 2271 – 2285. [5] CHAN W C, HSU Y Y. Automatic generation control of intercon- nected power systems using variable-structure controller [J]. IEE Pro- ceedings, Part C, 1981, 128(2): 269 – 279. [6] PAN C T, LIAW C M. An adaptive controller for power system load- frequency control [J]. IEEE Transactions on Power Systems, 1989, 4(1): 122 – 128. [7] WANG Y, ZHOU R, WEN C. Robust load-frequency controller de- sign for power systems [J]. IEE Proceedings, Part C, 1993, 140(1): 11 – 16. [8] WANG Z Q, SZNAIER M. Robust control design for load frequency control using µ-synthesis [C] //Southcon/94, Conference Record, Pis- cataway: IEEE, 1994: 186 – 190. [9] RAY G, PRASAD A N, PRASAD G D. A new approach to the design of robust load-frequency controller for large scale power systems [J]. Electric Power Systems Research, 1999, 51(1): 13 – 22. [10] TAN W. Tuning of PID load frequency controller for power sys- tems [J]. Energy Conversion & Management, 2009, 50(6): 1465 – 1472. [11] TAN W. Unified tuning of PID load frequency controller for power systems via IMC [J]. IEEE Transactions on Power Systems, 2010, 25(1): 341 – 350. [12] DONG L, ZHANG Y, GAO Z. A robust decentralized load frequency controller for interconnected power systems [J]. ISA Transactiions, 2012, 51(3): 410 – 419. (b) 联络线交换功率偏差 图 10 四区域电力系统响应 Fig. 10 Responses of the four-area power system
    分享到：
    赞 收藏

    相关推荐

    资料库

    安全技术

    共收录1285份资料，累计4个分类，关注成员有19位，主要包括：网络攻防,系统安全,其它,网络安全

    热门标签

    网络攻防 系统安全 其它 网络安全

    最新资料