2 2 2 2 2 2 2 第 28卷第 5期 2005年 10月 南 京 气 象 学 院 学 报 Journal of Nanjing Institute of Meteorology Vol. 28 No. 5 Oct. 2005 　　文章编号 : 1000 2022 (2005) 05 0685 05 图像小波域维纳滤波去噪算法的改进 严 　勇 , 　陈钟荣 (南京信息工程大学 电子工程系 ,江苏 南京 　210044) 摘 　要 :介绍了小波变换和维纳滤波相结合的图像小波域维纳滤波去噪算法 ,在分析 该算法最小均方误差期望的基础上提出一种改进算法 。指出在进行维纳滤波之前 , 阈值化处理可以有效提高维纳滤波的性能 。用标准测试图像的处理结果来比较改进 前后两种算法的效果 。 关键词 :图像去噪 ;小波 ;维纳滤波 ;阈值化 中图分类号 : TN911. 73　　文献标识码 : A 图像在采集 、转换 、传输 、压缩和储存等过程中 ,常会因成像设备与外部环境等因素的影响 而引入噪声 [ 1 ] 。因此 ,从被污染的图像中滤去噪声 ,提高图像的信噪比 ,突出图像的期望特 征 ,恢复图像的本来面目 ,是图像处理技术的一项重要内容 。数字图像处理至今已有 40多年 的发展历史 ,经典的去噪算法有很多 ,利用空间自适应统计算法去噪得到的结果较好 [ 2 ] 。近 年来 ,小波分析方法迅速崛起 ,被广泛应用于各个领域 ,在国际上形成了一股“小波热潮 ”[ 3 ] 。 小波变换类似于经典的傅里叶变换 ,但优于傅里叶变换 ,它在时域和频域上同时具有局部化特 性 ,被誉为“数学显微镜 ”[ 4 ] 。随着小波理论的不断发展 ,越来越多的小波性质被应用到图像 处理中 。小波域维纳滤波去噪算法就是小波理论在图像去噪处理中的一种应用 。杨龙平 等 [ 5 ] 、穆国燕等 [ 6 ]曾先后介绍过这一算法 ;马林立等 [ 7 ]将此算法应用于星图去噪中 ,并取得了 很好的效果 。 本文首先介绍小波域维纳滤波去噪算法 ,并在分析该算法最小均方误差的数学期望的基 础上对原算法进行了改进 。结果表明在维纳滤波之前 ,进行阈值化处理可以提高图像的峰值 信噪比 ( Peak Signal to Noise Ratio,简称 PSNR) ,并用标准测试图像的处理结果比较了两种算 法的效果 。 09 　　收稿日期 : 2004 　　基金项目 :国家自然科学基金资助项目 (40275010) 　　作者简介 :严 　勇 (1979 28;改回日期 : 2004 11 04 ) ,男 ,江苏昆山人 ,硕士 ,研究方向 :信号的采集与分析处理. E mail: zixialang 791007@ tom. com. © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

686 南京气象学院学报 第 28卷 　 1　小波域维纳滤波 1. 1　小波域维纳滤波去噪算法 小波域维纳滤波的过程 [ 5 6 ]如图 1所示 。 图 1　小波域维纳滤波去噪的过程 Fig. 1　Flow chart for wavelet domain image denoising using W iener filtering 假设待处理图像表示为 Y = X +N ;其中 , X 表示“干净 ”的图像 , N 是与 X 互不相关 、均值 为零 、方差为 σ2 的高斯噪声 。进行小波变换后可得 : y = x + n ,式中 y = W Y, x = W X, n = W N ,W 为小波变换的变换矩阵 。由小波变换的正交性可知 , n仍然是均值为零 、方差为 σ2 的 高斯变量 ,且与 x互不相关 。此时 ,维纳滤波的形式可简化为 a = E [ x2 ] / E [ y2 ], 　　^x = ay。 ( 1) 其中 E [ ]表示变量的数学期望 , ^x为 x的最优线性估计 。 考虑到 n和 x互不相关 ,因此有 ( 2) 　　可以逐个求得 E [ y2 ] ,对于位于坐标 ( i, j)处的 E [ y2 ] ,可利用 yi, j及其邻值估计得到 。为 了不失一般性 ,利用一个 ( 2R + 1) ×( 2R + 1)方形窗 (该窗的中心位于坐标 ( i, j)处 )中的 yi, j值 平均求得 E [ x2 ] = E [ y2 ] - σ2。 R R Q i, j = ∑ ∑ y2 i- k, j- 1 , k = - R l = - R qi, j = Q i, j /M , 　　M = ( 2R + 1) 2。 　　用 qi, j作为 E [ y2 i, j ]的近似估计值 ,即 E [ y2 i, j ]≈ qi, j ,代入 (2)式可得 E [ x2 再代入 (1)式 ,可得维纳滤波的各个系数为 i, j ] = qi, j - σ2 , ai, j = ( qi, j - σ2 ) qi, j 。 1. 2　最小均方误差期望 ( ELM S ) 维纳滤波的最小均方误差期望 (Least Mean Square Error)可定义如下 ELM SE = E [ ( xi, j - ai, j yi, j ) 2 ]。 令 bi, j =σ2 / qi, j ,结合 (6)式代入上式 　　为了简化 ,忽略各个下标 , (8)式又可改写为 ELM SE = E [ ( xi, j - (1 - bi, j ) ( xi, j + ni, j ) ) 2 ]。 ( 3) ( 4) ( 5) ( 6) ( 7) ( 8) ( 9) 　　当方形窗不是太小时 ,可认为 b与 x和 n是相互独立的 。这一假设完全可以接受 。将上 式展开 ,根据期望的性质 ,并将 (5)式代入 ,可得 ELM SE = E [ ( b ( x + n) - n) 2 ]。 (10) 　　由 (3)式及 bi, j的定义可得 bi, j = Mσ2 /Q i, j ,而变量 Q 是自由度为 M、方差为 2M q2 的 χ2 分 ELM SE = E [ b ]2 q +σ2 ( 1 - 2E [ b ] ) 。 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

2 786 (11) (12) 　第 5期 　 严 　勇等 :图像小波域维纳滤波去噪算法的改进 布变量 。根据概率论知识 [ 8 ] ,可以求得 E [ b ]和 E [ b2 ]的近似估计值 σ4 q2 。 , 　　E [ b2 ] = E [ b ] = 2 M σ4 q2 + σ2 q 　　将 (11)式代入 (10)式 ,可得 ELM S = 2 M σ4 q +σ2 - σ4 q 。 　　假设当 ELM S > E [ x2 ]时 ,线性预测的结果不理想 ,更好的处理方法是直接将 x置为 0,此即 为所谓的阈值化处理 。将 (5)式代入 ,可得下面的不等式 σ4 q 　　解此不等式 ,可得 (已经考虑 q > 0 ) 2 M + 2σ2 - σ4 q > q。 q > kσ2 , 　　k = 1 + 2 /M。 2　改进算法 根据上述分析 ,可以得到小波域中维纳滤波算法的改进算法 。 (1)选取合适的 M 值 ,根据 (3)式和 (4)式 ,由待处理图像的小波系数 y求各个 qi, j。 (2)根据 (14)式进行阈值化处理 。如果 qi, j > kσ2 ,则 ^xi, j = yi, j ;否则 ^xi, j = 0 。 (3)使用与步骤 (1)中相同的 M ,利用 ^xi, j再次求 qi, j。 (4)利用 (6)式进行维纳滤波 。考虑到 E [ x2 ] ≥ 0, 可使用下面的式子计算 ai, j = m ax ( qi, j - σ2 , 0) qi, j , 　　x l i, j = ai, j ^xi, j。 (13) (14) (15) 　　在 (15)式中 , x 在维纳滤波的系数 ai, j中了 。 l i, j表示最后估计值 ; ^xi, j可以用 yi, j来代替 ,因为阈值化处理的效果已经包含 3　实验结果 现分别用这两种算法对标准测试图像 (Woman)进行处理 。实验方法如下 :在标准图像中 加入高斯噪声 ,用两种算法对该“污染 ”图像进行去噪 ,并计算出各自的 PSNR ,其中小波使用 正交小波族“symm lets”中的“sym8”。整个过程在 MATLAB 环境下完成 [ 9 10 ] 。图 2给出了改 进算法较原算法所提高的 PSNR随噪声方差 σ2 的变化 。图 3给出了当噪声方差 σ2 = 50时的 处理结果 。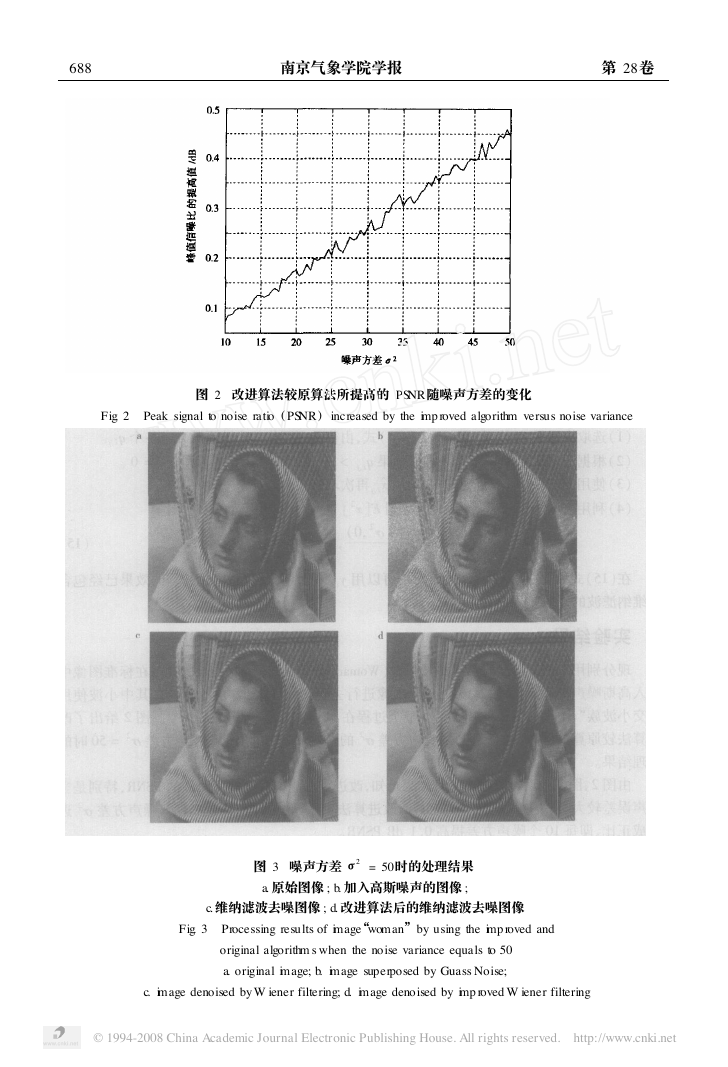 由图 2、图 3中两种算法的处理结果可知 ,改进算法能更好地提高图像的 PSNR ,特别是当 噪声误差较大时 。进一步分析图 2可知 ,改进算法较原算法的 PSNR提高值与噪声方差 σ2 近 似成正比 ,即每 10个噪声方差提高 0. 1 dB PSNR。 上面的实验仅仅是针对 Woman一幅图像的 ,为了进一步验证改进算法的效果 ,笔者又对 Lena、Barbara和 Saturn等测试图像在不同噪声方差 ( 10, 30, 50)下进行了实验 。很明显 ,使用 改进算法后 , 3幅图像的 PSNR都较原算法有一定提高 ,且提高值与噪声方差近似成正比 (表 1) 。 © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

886 南京气象学院学报 第 28卷 　 图 2　改进算法较原算法所提高的 PSNR随噪声方差的变化 Fig. 2　Peak signal to noise ratio ( PSNR) increased by the imp roved algorithm versus noise variance 图 3　噪声方差 σ2 = 50时的处理结果 a. 原始图像 ; b. 加入高斯噪声的图像 ; c. 维纳滤波去噪图像 ; d. 改进算法后的维纳滤波去噪图像 Fig. 3　Processing results of image“woman”by using the imp roved and original algorithm s when the noise variance equals to 50 a. original image; b. image superposed by Guass Noise; c. image denoised by W iener filtering; d. image denoised by imp roved W iener filtering © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

　第 5期 　 严 　勇等 :图像小波域维纳滤波去噪算法的改进 986 表 1　不同测试图像 、噪声方差下两种算法的 PSNR比较 Table 1　Comparison of PSNR s of original and imp roved algorithm s under the conditions of different test images and noise variances dB　　　 Lena图像的噪声方差 Barbara图像的噪声方差 Saturn图像的噪声方差 10 30 50 10 30 50 10 30 50 原算法 PSNR 改进算法 PSNR PSNR提高值 35 42 30 27 25 86 33 76 28 25 24 14 32 29 27 83 23 55 35 50 30 54 26 37 33 87 28 59 24 66 32 38 28 13 24 08 0 08 0 27 0 51 0 11 0 34 0 52 0 09 0 30 0 53 4　结 　论 提出了图像小波域维纳滤波去噪算法的一种改进算法 ,指出在维纳滤波之前 ,对图像的小 波变换系数进行阈值化处理 ,可以有效提高图像的 PSNR。由实验结果可知 ,该改进算法效果 良好 (尤其在噪声方差较大的情况下 ,效果更佳 ) ,计算量不大 ,是图像去噪的一种实用方法 。 参考文献 : [ 1 ] 　陈廷标 ,夏良正. 数字图像处理 [M ]. 北京 :人民邮电出版社 , 1994: 227 [ 2 ] 　M ihcak M K, Kozinsev I, Ramchandran K. Low 228. comp lexity image denoising based on statistical modeling of wavelet coefficients [ J ]. IEEE Signal Processing Letters, 1999, 6 (12) : 300 303. [ 3 ] 　王建忠. 小波理论及其在物理和工程中的应用 [ J ]. 数学进展 , 1992, 21 (3) : 289 [ 4 ] 　陈武凡. 小波分析及其在图像处理中的应用 [M ]. 北京 :科学出版社 , 2002: 156 [ 5 ] 　杨龙平 ,丁宣浩 ,孙建明. 一种新的基于小波变换的图像消噪方法 [ J ]. 云南民族大学学报 , 2005, 14 (1) : 71 [ 6 ] 　穆国燕 ,陈树中. 图像去噪的一种新方法 [ J ]. 计算机工程 , 2003, 29 (5) : 134 [ 7 ] 　马林立 ,孙 　尧. 小波域中的维纳滤波法在星图降噪中的应用 [ J ]. 红外与激光工程 , 2004, 33 (1) : 55 [ 8 ] 　盛 　骤 ,谢式千 ,潘承毅. 概率论与数理统计 [M ]. 北京 :高等教育出版社 , 1999: 99 [ 9 ] 　张志涌. 精通 MATLAB6 320. [ 10 ] 　孙兆林. MATLAB6. X图像处理 [M ]. 北京 :清华大学出版社 , 2002: 215 5版 [M ]. 北京 :北京航空航天大学出版社 , 2003: 310 135. 316. 159. 228. 74. 58. 115. The Improvement of Wavelet Doma in Image Denoising Algorithm by W iener Filtering YAN Yong, 　CHEN Zhong rong (Department of Electronic Engineering, NU IST, Nanjing　210044, China) Abstract: The wavelet domain image denosing algorithm combining wavelet transform w ith W iener filtering is first introduced in this paper. Based on the app roximate analysis of its least mean square error (LMSE) expectation ( ELM SE ) , an imp roved algorithm is p roposed. It is pointed out that a thresh olding operation before W iener filtering can effectively imp rove the performance of W iener filtering. The denoising effect of original and imp roved algorithm s is also compared using p rocessing results of a standard test image. Key words: image denosing; wavelet;W iener filtering; thresholding © 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net