logo资料库

Fractional Differential Equations in Matlab.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书 资料大小：0.64M 资料格式：pdf 举报 版权申诉
第1页 / 共28页
第2页 / 共28页
第3页 / 共28页
第4页 / 共28页
第5页 / 共28页
第6页 / 共28页
第7页 / 共28页
第8页 / 共28页
资料共28页，剩余部分请下载后查看
    0FractionalDerivatives,FractionalIntegrals,andFractionalDifferentialEquationsinMatlabIvoPetrášTechnicalUniversityofKošiceSlovakRepublic1.IntroductionThetermfractionalcalculusismorethan300yearsold.Itisageneralizationoftheordinarydifferentiationandintegrationtonon-integer(arbitrary)order.ThesubjectisasoldasthecalculusofdifferentiationandgoesbacktotimeswhenLeibniz,Gauss,andNewtoninventedthiskindofcalculation.InalettertoL’Hospitalin1695Leibnizraisedthefollowingquestion(MillerandRoss,1993):“Canthemeaningofderivativeswithintegerorderbegeneralizedtoderivativeswithnon-integerorders?"ThestorygoesthatL’HospitalwassomewhatcuriousaboutthatquestionandrepliedbyanotherquestiontoLeibniz.“Whatiftheorderwillbe1/2?"LeibnizinaletterdatedSeptember30,1695replied:“Itwillleadtoaparadox,fromwhichonedayusefulconsequenceswillbedrawn."ThequestionraisedbyLeibnizforafractionalderivativewasanongoingtopicinthelast300years.Severalmathematicianscontributedtothissubjectovertheyears.PeoplelikeLiouville,Riemann,andWeylmademajorcontributionstothetheoryoffractionalcalculus.ThestoryofthefractionalcalculuscontinuedwithcontributionsfromFourier,Abel,Leibniz,Grünwald,andLetnikov.Nowadays,thefractionalcalculusattractsmanyscientistsandengineers.Thereareseveralapplicationsofthismathematicalphenomenoninmechanics,physics,chemistry,controltheoryandsoon(Caponettoetal.,2010;Magin,2006;Monjeetal.,2010;OldhamandSpanier,1974;Oustaloup,1995;Podlubny,1999).Itisnaturalthatmanyauthorstriedtosolvethefractionalderivatives,fractionalintegralsandfractionaldifferentialequationsinMatlab.AfewverygoodandinterestingMatlabfunctionswerealreadysubmittedtotheMathWorks,Inc.MatlabCentralFileExchange,wheretheyarefreelydownloadableforsharingamongtheusers.Inthischapterwewillusesomeofthem.ItisworthmentioningsomeadditiontoMatlabtoolboxes,whichareappropriateforthesolutionoffractionalcalculusproblems.OneofthemisatoolboxcreatedbyCRONEteam(CRONE,2010)andanotheroneistheFractionalState–SpaceToolkitdevelopedbyDominikSierociuk(Sierociuk,2005).LastbutnotleastweshouldalsomentionaMatlabtoolboxcreatedbyDingyüXue(Xue,2010),whichisbasedonMatlabobjectforfractional-ordertransferfunctionandsomemanipulationwiththisclassofthetransferfunction.Despitethatthementionedtoolboxesaremainlyforcontrolsystems,theycanbe“abused"forsolutionsofgeneralproblemsrelatedtofractionalcalculusaswell.10www.intechopen.com
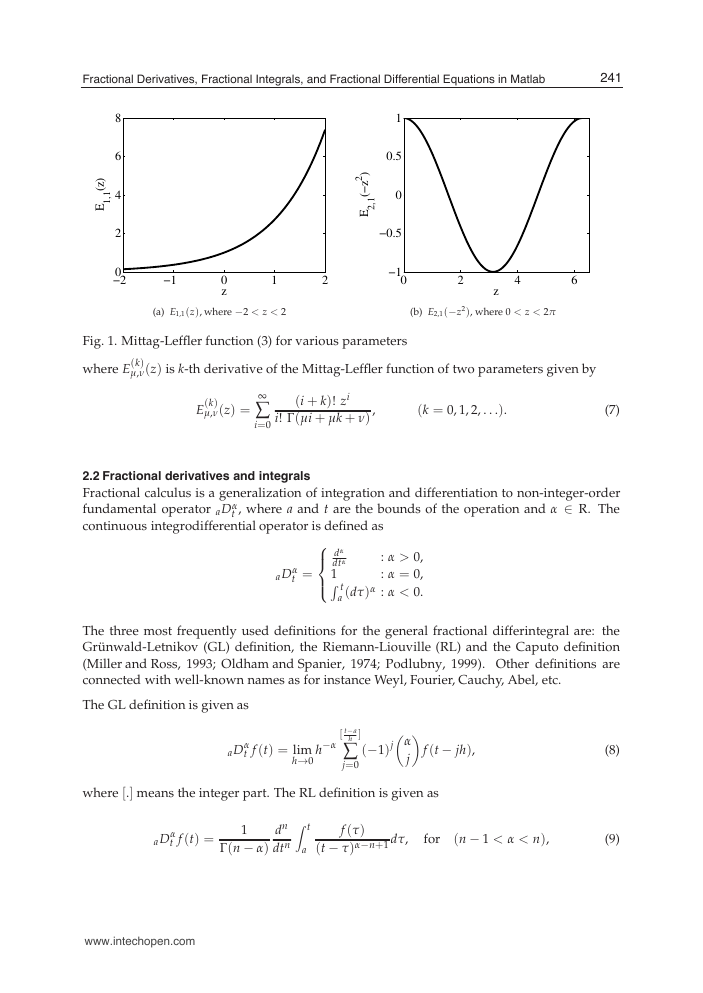
    2Will-be-set-by-IN-TECH2.Fractionalcalculusfundamentals2.1SpecialfunctionsHereweshouldmentionthemostimportantfunctionusedinfractionalcalculus-Euler’sgammafunction,whichisdefinedasΓ(n)=∞0tn−1e−tdt.(1)Thisfunctionisageneralizationofthefactorialinthefollowingform:Γ(n)=(n−1)!(2)ThisgammafunctionisdirectlyimplementedintheMatlabwithsyntax[]=gamma().Anotherfunction,whichplaysaveryimportantroleinthefractionalcalculus,wasinfactintroducedin1953.Itisatwo-parameterfunctionoftheMittag-Lefflertypedefinedas(Podlubny,1999):Eα,β(z)=∞∑k=0zkΓ(αk+β),(α>0,β>0).(3)TheMittag-Lefflerfunction(3)canbeexpressedintheintegralrepresentationasEα,β(z)=12πiCtα−βettα−zdt,(4)thecontourCstartsandendsat−∞andcirclesaroundthesingularitiesandbranchpointsoftheintegrand.Therearesomerelationships(givene.g.in(Djrbashian,1993;Podlubny,1999)):E1,1(z)=ez,E1/2,1(√z)=2√πe−zerfc(−√z),E2,1(z)=cosh(√z),E2,1(−z2)=cos(z),E1,2(z)=ez−1z.Forβ=1weobtaintheMittag-Lefflerfunctioninoneparameter(Podlubny,1999):Eα,1(z)=∞∑k=0zkΓ(αk+1)≡Eα(z).(5)ForthenumericalevaluationoftheMittag-Lefflerfunction(3)withthedefaultaccuracysetto10−6theMatlabroutine[e]=mlf(alf,bet,c,fi),writtenbyPodlubnyandKacenak(2005)canbeused.AnotherMatlabfunctionf=gml_fun(a,b,c,x,eps0)forageneralizedMittag-LefflerfunctionwascreatedbyYangQuanChen(Chen,2008).InFig.1(a)andFig.1(b)areplottedthewell-knownfunctions(ezandcos(z))computedviatheMatlabroutine[]=mlf()createdfortheevaluationoftheMittag-Lefflerfunction.AnotherimportantfunctionEk(t,λ;μ,ν)oftheMittag-Lefflertypewasintroducedby(Podlubny,1999).ThefunctionisdefinedbyEk(t,λ;μ,ν)=tμk+ν−1E(k)μ,ν(λtμ),(k=0,1,2,...),(6)240Engineering Education and Research Using MATLABwww.intechopen.com
    FractionalDerivatives,FractionalIntegrals,andFractionalDifferentialEquationsinMatlab3−2−101202468zE1,1(z)(a)E1,1(z),where−20,1:α=0,ta(dτ)α:α<0.Thethreemostfrequentlyuseddefinitionsforthegeneralfractionaldifferintegralare:theGrünwald-Letnikov(GL)definition,theRiemann-Liouville(RL)andtheCaputodefinition(MillerandRoss,1993;OldhamandSpanier,1974;Podlubny,1999).Otherdefinitionsareconnectedwithwell-knownnamesasforinstanceWeyl,Fourier,Cauchy,Abel,etc.TheGLdefinitionisgivenasaDαtf(t)=limh→0h−α[t−ah]∑j=0(−1)jαjf(t−jh),(8)where[.]meanstheintegerpart.TheRLdefinitionisgivenasaDαtf(t)=1Γ(n−α)dndtntaf(τ)(t−τ)α−n+1dτ,for(n−1<α
    4Will-be-set-by-IN-TECHwhereΓ(.)isthegammafunction.TheCaputodefinitionoffractionalderivativescanbewrittenasaDαtf(t)=1Γ(n−α)taf(n)(τ)(t−τ)α−n+1dτ,for(n−1<α
    FractionalDerivatives,FractionalIntegrals,andFractionalDifferentialEquationsinMatlab5theformofIIRandFIRapproximationstogetherwithillustrativeexamples.SomeofthementionedfrequencymethodsinbothformsofapproximationhavebeenrealizedastheMatlabroutinesinDuarteValerio’stoolboxcalledninteger(seedetailreviewin(Valério,2005)).AlsocreatedinthistoolboxwasaSimulinkblocknidforfractionalderivativeandintegral,wheretheorderofderivative/integralandmethodofitsapproximationcanbeselected.2.3.1Grünwald-LetnikovmethodFornumericalcalculationoffractional-orderderivativeswecanusetherelation(13)derivedfromtheGLdefinition(8).Thisapproachisbasedonthefactthatforawideclassoffunctionsthethreedefinitions-GL(8),RL(9),andCaputo’s(10)-areequivalentiff(a)=0.Therelationfortheexplicitnumericalapproximationofq-thderivativeatthepointskh,(k=1,2,...)hasthefollowingform(Dorˇcák,1994;Podlubny,1999):(k−Lm/h)Dqtkf(t)≈h−qk∑j=0(−1)jqjf(tk−j)=h−qk∑j=0c(q)jf(tk−j),(13)whereLmisthe“memorylength",tk=kh,histhetimestepofcalculationandc(q)j(j=0,1,...,k)arebinomialcoefficients.Fortheircalculationwecanuseforinstancethefollowingexpression(Dorˇcák,1994):c(q)0=1,c(q)j=1−1+qjc(q)j−1.(14)Thebinomialcoefficientsc(q)j(j=0,1,...,k)canbealsoexpressedbyusingafactorial.Writingthefactorialasagammafunction(2),itallowsthebinomialcoefficienttobegeneralizedtonon-integerarguments.Wecanwritetherelations:(−1)jqj=(−1)jΓ(q+1)Γ(j+1)Γ(q−j+1)=Γ(j−q)Γ(−q)Γ(j+1).(15)Obviously,forthissimplificationwepayapenaltyintheformofsomeinaccuracy.Iff(t)≤M,wecaneasilyestablishthefollowingestimatefordeterminingthememorylengthLm,providingtherequiredaccuracyǫ:Lm≥Mǫ|Γ(1−q)|1/q.(16)Theabove-describednumericalmethodiscalledPowerSeriesExpansion(PSE)ofageneratingfunction.ItisimportanttonotethatPSEleadstoapproximationintheformofpolynomials,thatis,thediscretizedfractionaloperatorisintheformofFIRfilter,whichhasonlyzeros(ChenandMoore,2002;Vinagreetal.,2003).Theresultingdiscretetransferfunction,approximatingfractional-orderoperators,canbeexpressedinz-domainasfollows:0D±rkTG(z)=Y(z)F(z)=1T±rPSE1−z−1±rn≈T∓rRn(z−1),(17)243Fractional Derivatives, Fractional Integrals, and Fractional Differential Equations in Matlabwww.intechopen.com
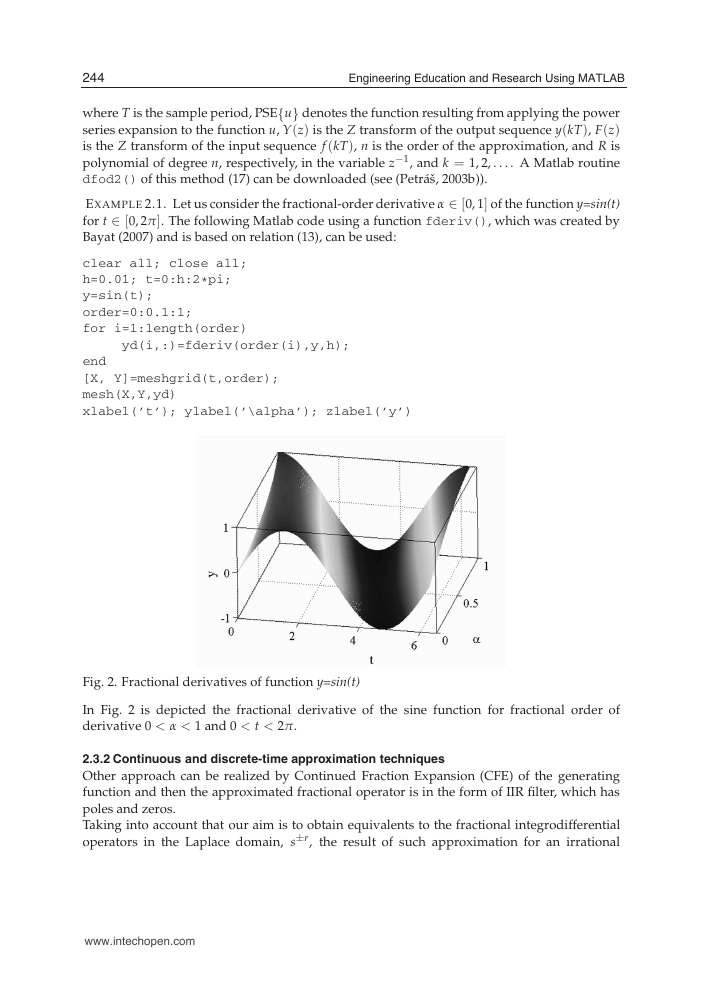
    6Will-be-set-by-IN-TECHwhereTisthesampleperiod,PSE{u}denotesthefunctionresultingfromapplyingthepowerseriesexpansiontothefunctionu,Y(z)istheZtransformoftheoutputsequencey(kT),F(z)istheZtransformoftheinputsequencef(kT),nistheorderoftheapproximation,andRispolynomialofdegreen,respectively,inthevariablez−1,andk=1,2,....AMatlabroutinedfod2()ofthismethod(17)canbedownloaded(see(Petráš,2003b)).EXAMPLE2.1.Letusconsiderthefractional-orderderivativeα∈[0,1]ofthefunctiony=sin(t)fort∈[0,2π].ThefollowingMatlabcodeusingafunctionfderiv(),whichwascreatedbyBayat(2007)andisbasedonrelation(13),canbeused:clearall;closeall;h=0.01;t=0:h:2*pi;y=sin(t);order=0:0.1:1;fori=1:length(order)yd(i,:)=fderiv(order(i),y,h);end[X,Y]=meshgrid(t,order);mesh(X,Y,yd)xlabel(’t’);ylabel(’\alpha’);zlabel(’y’)Fig.2.Fractionalderivativesoffunctiony=sin(t)InFig.2isdepictedthefractionalderivativeofthesinefunctionforfractionalorderofderivative0<α<1and0
    FractionalDerivatives,FractionalIntegrals,andFractionalDifferentialEquationsinMatlab7function,G(s),canbeexpressedintheform(Vinagreetal.,2003):G(s)≃a0(s)+b1(s)a1(s)+b2(s)a2(s)+b3(s)a3(s)+...=a0(s)+b1(s)a1(s)+b2(s)a2(s)+b3(s)a3(s)+...(18)whereaisandbisarerationalfunctionsofthevariables,orareconstants.Theapplicationofthemethodyieldsarationalfunction,whichisanapproximationoftheirrationalfunctionG(s).Inotherwords,forevaluationpurposes,therationalapproximationsobtainedbyCFEfrequentlyconvergemuchmorerapidlythanthePSEandhaveawiderdomainofconvergenceinthecomplexplane.Ontheotherhand,theapproximationbyPSEandtheshortmemoryprincipleisconvenientforthedynamicalpropertiesconsideration.Forinterpolationpurposes,rationalfunctionsaresometimessuperiortopolynomials.Thisis,roughlyspeaking,duetotheirabilitytomodelfunctionswithpoles.Thesetechniquesarebasedontheapproximationsofanirrationalfunction,G(s),byarationalfunctiondefinedbythequotientoftwopolynomialsinthevariablesinfrequencys-domain:G(s)≃Ri(i+1)...(i+m)=Pμ(s)Qν(s)=p0+p1s+...+pμsμq0+q1s+...+qνsν,(m+1=μ+ν+1)(19)passingthroughthepoints(si,G(si)),...,(si+m,G(si+m)).Theresultingdiscretetransferfunction,approximatingfractional-orderoperators,canbeexpressedas(Vinagreetal.,2003):0D±rkTG(z)=Y(z)F(z)=2T±rCFE⎧⎨⎩1−z−11+z−1±r⎫⎬⎭p,n≈2T±rPp(z−1)Qn(z−1),(20)whereTisthesampleperiod,CFE{u}denotesthefunctionresultingfromapplyingthecontinuedfractionexpansiontothefunctionu,Y(z)istheZtransformoftheoutputsequencey(kT),F(z)istheZtransformoftheinputsequencef(kT),pandnaretheordersoftheapproximation,andPandQarepolynomialsofdegreespandn,respectively,inthevariablez−1,andk=1,2,....Ingeneral,thediscretizationoffractional-orderdifferentiator/integrators±r(r∈R)canbeexpressedbythegeneratingfunctions≈ω(z−1).Thisgeneratingfunctionanditsexpansiondetermineboththeformoftheapproximationandthecoefficients(Lubich,1986).Inthissection,fordirectdiscretizingsr,(0
    8Will-be-set-by-IN-TECHwhereaistheratiotermandristhefractionalorder.Theratiotermaistheamountofphaseshiftandthistuningknobissufficientformostengineeringproblemsbeingsolved.Inexpandingtheaboveinrationalfunctions,wewillusetheCFE.Itshouldbepointedoutthat,forcontrolapplications,theobtainedapproximatediscrete-timerationaltransferfunctionshouldbestable.Furthermore,forabetterfittothecontinuousfrequencyresponse,itwouldbeofhighinteresttoobtaindiscreteapproximationswithpolesanzerosinterlacedalongthelinez∈(−1,1)ofthezplane.Thedirectdiscretizationapproximationsproposedinthispaperenjoythedesiredproperties.Theresultofsuchapproximationforanirrationalfunction,G(z−1),canbeexpressedbyG(z−1)intheCFEform(Vinagreetal.,2000):G(z−1)≃a0(z−1)+b1(z−1)a1(z−1)+b2(z−1)a2(z−1)+b3(z−1)a3(z−1)+...=a0(z−1)+b1(z−1)a1(z−1)+b2(z−1)a2(z−1)+...b3(z−1)a3(z−1)+...whereaiandbiareeitherrationalfunctionsofthevariablez−1orconstants.Theapplicationofthemethodyieldsarationalfunction,G(z−1),whichisanapproximationoftheirrationalfunctionG(z−1).Theresultingdiscretetransferfunction,approximatingfractional-orderoperators,canbeexpressedas:(ω(z−1))±r≈1+aT±rCFE⎧⎨⎩1−z−11+az−1±r⎫⎬⎭p,q=1+aT±rPp(z−1)Qq(z−1),=1+aT±rp0+p1z−1+···+pmz−pq0+q1z−1+···+qnz−q,(22)whereCFE{u}denotesthecontinuedfractionexpansionofu;pandqaretheordersoftheapproximationandPandQarepolynomialsofdegreespandq.Normally,wecansetp=q=n.AMatlabroutinedfod1()forthisdescribedmethod(22)canbedownloaded(see(Petráš,2003a)).EXAMPLE2.2.Herewepresentsomeresultsforfractionalorderr=±0.5(half-orderderivative/integral).Thevalueofapproximationordernistruncatedton=3andweightingfactorawaschosena=1/3.AssumesamplingperiodT=0.001sec.Forr=0.5wehavethefollowingapproximationofthefractionalhalf-orderderivative:G(z−1)=985.9−1315z−1+328.6z−2+36.51z−327−18z−1−3z−2+z−3(23)AMatlabsequenceforthethefractionalhalf-orderderivativeapproximation(23)follows:sys=dfod1(3,0.001,1/3,0.5)bode(sys)step(sys)246Engineering Education and Research Using MATLABwww.intechopen.com
    分享到：
    赞 收藏

    相关推荐

    资料库

    人工智能

    共收录2047份资料，累计62个分类，关注成员有19位，主要包括：GNSS,Pico-SIM868-GSM,GPRS,NB-IoT,GPRSHAT,SIM7070GCat-M,GNSSHAT,GSM,NB-IoTHAT,SIM7080GCat-M,R800CGSM,SIM800CGSM,UPSPowerModule(B),UPSPowerModule,Pico-SIM7020C-NB-IoT,SIM7028NB-IoTHAT,SIM7020CNB-IoTHAT,SIM7000XNB-IoTHAT,A7670CCat-1HAT,A7600C1Cat-1,SIM7600X4G&amp;LTECat-1HAT,SIM7600X4GDONGLE用户手册,RM520N-GL5GHAT,RM500Q-GL5GHAT,RM500U-CN5GHAT,SIM820X-M25GforJetsonNano,AudioCardforJetsonNano,SIM7600G-H4GforJetsonNano,OpenNCC-Lite-4G8M,IMX219-77Camera,13.3inche-PaperHAT,10.3inche-PaperHAT(D),10.3inche-PaperHAT,9.7inche-PaperHAT,7.8inche-PaperHAT,6inchHDTouche-PaperHAT,6inchHDe-PaperHAT,6inche-PaperHAT,5.83inche-PaperHAT(C),LCD-Clock-A,0.95inchRGBOLED(A),0.96inchRGBOLEDModule,0.96inchOLEDModule,0.96inchOLED(A),1.27inchRGBOLEDModule,1.3inchOLEDModule(C),1.3inchOLED(A),1.32inchOLEDModule,1.5inchRGBOLEDModule,1.5inchOLEDModule,JETSONORINNX,自然语言处理,搜索引擎,VR,计算广告,深度学习,机器学习

    热门标签

    GNSS Pico-SIM868-GSM GPRS NB-IoT GPRSHAT SIM7070GCat-M GNSSHAT GSM NB-IoTHAT SIM7080GCat-M R800CGSM SIM800CGSM UPSPowerModule(B) UPSPowerModule Pico-SIM7020C-NB-IoT SIM7028NB-IoTHAT SIM7020CNB-IoTHAT SIM7000XNB-IoTHAT A7670CCat-1HAT A7600C1Cat-1 SIM7600X4G&amp;LTECat-1HAT SIM7600X4GDONGLE用户手册 RM520N-GL5GHAT RM500Q-GL5GHAT RM500U-CN5GHAT SIM820X-M25GforJetsonNano AudioCardforJetsonNano SIM7600G-H4GforJetsonNano OpenNCC-Lite-4G8M IMX219-77Camera 13.3inche-PaperHAT 10.3inche-PaperHAT(D) 10.3inche-PaperHAT 9.7inche-PaperHAT 7.8inche-PaperHAT 6inchHDTouche-PaperHAT 6inchHDe-PaperHAT 6inche-PaperHAT 5.83inche-PaperHAT(C) LCD-Clock-A 0.95inchRGBOLED(A) 0.96inchRGBOLEDModule 0.96inchOLEDModule 0.96inchOLED(A) 1.27inchRGBOLEDModule 1.3inchOLEDModule(C) 1.3inchOLED(A) 1.32inchOLEDModule 1.5inchRGBOLEDModule 1.5inchOLEDModule JETSONORINNX 自然语言处理 搜索引擎 VR 计算广告 深度学习 机器学习

    最新资料