logo资料库

三维高速机动目标跟踪交互式多模型算法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.55M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    第 25 卷第 5 期 2008 年 10 月 控 制 理 论 与 应 用 Control Theory & Applications Vol. 25 No. 5 Oct. 2008 文文文章章章编编编号号号: 1000−8152(2008)05−0831−06 三三三维维维高高高速速速机机机动动动目目目标标标跟跟跟踪踪踪交交交互互互式式式多多多模模模型型型算算算法法法 彭冬亮, 郭云飞, 薛安克 (杭州电子科技大学 信息与控制研究所, 浙江 杭州 310018) 摘要: 对三维机动目标, 尤其是高速机动目标的跟踪一直是目标跟踪领域的重点和难点, 通过二维或解耦 模型扩展并不一定能满足精度要求. 提出了一种基于常速模型、 “当前” 统计模型、带约束的三维常速率协同 转弯模型的交互式多模型算法. 通过对包括匀加速模型、Singer模型、“当前” 统计模型在内的不同模型组合进 行 Monte-Carlo 仿真比较表明本算法对三维高速机动目标跟踪是有效性, 并具有很好的实用性. 关键词: 三维常速率协同转弯模型; 高速机动目标跟踪; 交互式多模型 中图分类号: TP273 文献标识码: A An interacting multiple model algorithm for a 3D high maneuvering target tracking PENG Dong-liang, GUO Yun-fei, XUE An-ke (Institute of Information and Control, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China) Abstract: The major challenge in target tracking occurs when the target is flying or turning at high speeds in the 3D space. In this situation, a 2D model or an extended decoupled-model may lead to an unacceptably low accuracy. To address this problem, we propose an Interacting Multiple Model (IMM) algorithm that includes a 3D constant velocity model (CV), a 3D “current”statistical model (CSM), and a 3D coordinated turning-model (3DCSCT) with kinematical constants of a constant speed target. The tracking performance of the proposed IMM algorithm is compared with that of an IMM algorithm utilizing CV, 3DCSCT, and constant acceleration model (CA) or Singer model. Simulation results demonstrate that the algorithm is feasible and practical for a 3D high maneuvering target tracking. Key words: 3D constant speed coordinate turn model; high maneuvering target tracking; IMM 1 引引引言言言(Introduction) 高速机动目标跟踪是目标跟踪领域的研究重点 和难点之一. 国内外大量的研究、仿真都集中在二 维平面. 对于在垂直方向很少机动的目标 (如民航 飞机), 通过假设 z 轴方向匀速或者只受随机噪声 干扰, 将二维模型或跟踪算法推广到三维情况可以 满足跟踪精度的要求[1]. 但是现实中的许多机动目 标经常在三维空间做高速机动 (如战斗机高速机 动). 此时通过二维模型和算法的扩展往往达不到跟 踪精度要求. 因此对三维空间机动目标跟踪算法的 研究具有重要的现实意义. 交互式多模型方法 (IMM) 是一种最具费效比且 适合工程应用的机动目标跟踪算法[2,3]. 它通过建 立一组模型集来并行跟踪目标, 目标运动状态的最 终估计是所有参与估计的模型滤波器输出的加权 和. 用 IMM 方法跟踪三维高速机动目标的关键问题 之一就是寻找与目标运动模式匹配的模型集合. 弯运动的模型匹配问题, 目标协同转弯时的加速度 向量是时变的. 如果用通常的机动模型, 如匀加速模 型 (CA)、Singer 模型、“当前”统计模型 (CSM) 等跟 踪协同转弯运动会出现比较大的误差[4]. 本文选用 三维常速率协同转弯模型 (3DCSCT) 来匹配协同转 弯运动, 并加入运动约束 (kinematic constraint) 滤 波, 有效降低了由模型不匹配引入的误差[4]. 通过 对3种 IMM 滤波器跟踪三维高速机动目标性能的 仿真比较, 结果表明由常速模型 (CV)、CSM 模型 和 3DCSCT 模型组合构成的IMM滤波器具有良好 的跟踪性能. 2 三三三维维维机机机动动动模模模型型型(3-D maneuvering model) 2.1 匀匀匀加加加速速速模模模型型型(Constant acceleration model, CA) 匀加速模型假设加速度的1阶导数是白噪声过 程, 即: ˙a(t) = w(t). (1) 对于三维机动目标, 需要特别关注的是协同转 w(t) 是均值为零, 方差为 σ2 的高斯白噪声. 则单维 收稿日期: 2007−07−06; 收修改稿日期: 2008−03−31. 基金项目: 国家自然科学基金资助项目(60602049, 60434020).
    832 的连续状态方程为: ˙x1(t) = 其中 x1(t) = 其中: 0 1 0 0 1 0 0 0  x1(t) +  w(t). 0 1 0 0 T, 相应的离散形式为: 1 T  . x, ˙x, ¨x F (k) = T 2 2 0 1 T 0 0 1 x1(k) = F (k)x1(k − 1) + w(k). (2) (3) (4) 对应的三维扩展模型为: x(k)=diag F (k), F (k), F (k) 其中 x(k) = (x, 2.2 Singer模模模型型型(Singer model) ˙x, ¨x, y, ˙y, ¨y, z, x(k−1)+w(k). (5) ˙z, ¨z )T. 1970年 由 Singer 提 出 的 一 阶 时 间 相 关 模 型[5] (Singer模型), 它假设目标加速度 a(t)是零均值一 阶 Markov 过程, 设加速度的时间相关函数为指数衰 减形式: Rα(τ) = E{α(t)α(t + τ)} = σ2 αe−α|τ|, α 0. (6) α, α 为在区间 (t, t + τ) 内决定目标机动特 式中σ2 性的待定参数. σ2 α 为机动加速的方差: α 为机动 时间常数, 即机动频率. α = , 它的确切值只有 通过实时测量才能确定. 一般经验取值为: 转弯机 动 α = , 大气扰动 α = 1. , 逃避机动 α = 1 τ 1 60 1 20 用 Wiener-Kolmogorov 方 法 对 时 间 相 关 函 数 Rα(t)白 化 后, 其 机 动 加 速 度 a(t) 可 用 输 入 为 白噪声的一阶时间相关模型来表示, 即: ˙a(t) = −αa(t) + w(t), 其中w(t) 是均值为零, 方差为 2ασ2 α 的高斯白噪 声. 于是, 以白噪声驱动的单维连续 Singer 模型为: (7)  x1(t) + 0  w(t). 0 1 0 0 0 1 0 0 − α ˙x1(t) = 0 1 对应的离散形式为: x1(k) = F (k)x1(k − 1) + w(k). 其中: F (k) = 1 T 0 1 0 0  , αT − 1 + e−αT α2 1 − e−αT α e−αT (8) (9) (10) α T − 1 − e−αT α 1 − e−αT 推广到三维的离散形式: x(k) = diag diag F (k), F (k), F (k) U(k), U(k), U(k) x(k − 1) + ¯a(k)+w(k). (19) 控 制 理 论 与 应 用 第 25 卷 推广到三维情况的离散形式为: x(k) = diag F (k), F (k), F (k) x(k − 1) + w(k). (11) Singer模型用有色噪声来描述机动加速度更切 合实际, 因此得到广泛的应用. 2.3 “当当当 前前前” 统统统 计计计 模模模 型型型 (“Current” statistic model, CSM) 在具体的一个作战场合, 当目标正以某一加速度 机动时, 下一时刻的加速度取值是有限的, 且只能 处在 “当前” 加速度附近. 因此, 我国学者周宏仁提 出了 “当前” 统计模型[6]. 该模型本质上是非零均值 时间相关模型, 其机动加速度的 “当前” 概率密度用 修正的瑞利分布描述, 均值为 “当前” 加速度预测 值. 随机加速度在时间轴上仍然符合一阶时间相关 过程, 即: ¨x(t) = ¯a(t) + a(t), ˙a(t) = −αa(t) + w(t). (12) (13) 式中¯a(t) 为机动加速度 “当前” 均值, 在每一采样周 期内为常数. α, w(t) 的假设与 Singer 模型相同. 令 a1(t) = ¯a(t) + a(t) 代入式(12)和(13), 可得: (14) (15) ¨x(t) = a1(t), ˙a1(t) = −αa1(t) + α¯a(t) + w(t). 将(14)和(15)两式写为状态方程, 则可得单维机动目 标的“当前”统计模型.  x1+  0  ¯a(t)+ 0  w(t). ˙x1(t)= 0 1 0 0 0 1 0 0 −α 0 α 0 1 相应的离散形式为: x1(k) = F (k)x1(k − 1) + U(k)¯a(k) + w(k). 其中:  , αT − 1 + e−αT α2 1 − e−αT α e−αT 0 1 0 0 −T +αT 2/2+(1−e−αT )/α F (k) = U(k)= (16) (17) . (18) 1 T 
    第 5 期 2.4 常常常速速速率率率协协协同同同转转转弯弯弯模模模型型型(Constant speed coordi- nate turn, CSCT) 常速率协同转弯模型假设目标以一个常速率 (即 速度和加速度垂直) 在一个平面内 (不一定是水平 面) 做圆周运动[1,4]. 对于在任意平面内的机动目标, 其加速度为: a = Ω × v. (20) 式中 Ω 是角速度向量, v 为速度向量. 对(20)求导可 得: ˙a = (Ω · v)Ω − (Ω · Ω)v. 由假设目标的运动轨迹是在同一个平面内, 则 Ω 垂 直于 a 与 v 决定的平面, 即 Ω⊥v. 因此有: ˙a = −ω2v. 其中 ω 定义为: ω Ω = a v = a v . 若加速度受到白噪声干扰, 即: ˙a = −ω2v + w. w 为白噪声. 当状态向量 x = (x, ˙x, ¨x, y, ˙y, ¨y, z, ˙z, ¨z)T 时, 对应于三维连续 CSCT 模型为: ˙x(t) = diag diag A(ω), A(ω), A(ω) B, B, B w(t). x(t) + 0 1 0 0 0 1 0 −ω2 0 0 0 1  , B = 其中: A(ω) =  . (25) (26) x(k − 1) + w(k). (27)  . (28) 1 对应的离散形式为: x(k) = diag F (ω), F (ω), F (ω) 式中: F (ω) = sin (ωT ) 1 − cos (ωT ) ω 0 cos (ωT ) 0 −ω sin (ωT ) ω2 sin (ωT ) ω cos (ωT ) T 为采样周期. 式(27)描述的模型与参数 ω 有很大关系, 其可以 由式(23)用加速度与速度的比值来计算. 这样在已 知 ω 的情况下, 能保持滤波方程是线性的. 在这个 模型中, 速度和加速度估计值的精度将直接影响 到 ω, 进而影响到模型的精度. 特别是当模型前提假 设条件不满足时: 即a · v = 0 不成立, 将对滤波精度 产生较大影响, 在滤波器初始化时特别容易引起发 彭冬亮等: 三维高速机动目标跟踪交互式多模型算法 (21) (22) (23) (24) 833 散. 已知有效的解决方法是把 a · v = 0 作为运动约 束加入滤波过程中[7,8]. 3 IMM算算算法法法(IMM algorithm) 考虑一个典型的目标跟踪系统离散模型, 其状态 方程和量测方程分别为: (29) (30) x(k) = F (k)x(k − 1) + w(k), z(k) = H(k)x(k) + v(k). T; F (k)为状态 x, ˙x, ¨x, y, ˙y, ¨y, z, ˙z, ¨z 其中, 状态向量 x(k)由位置、速度和加速度组成, 即 x(k) = 转 移 矩 阵; z(k)为 目 标 量 测 向 量; H(k)为 量 测 矩 阵；w(k), v(k)为相互独立的零均值高斯白噪声, 其 协方差矩阵分别为 Q(k) 和 R(k). IMM跟踪算法的实质是, 由前一时刻每个模型 的输出加权组合作为各个模型的当前输入, 多个模 型并行估计, 最后得到组合状态估计. 设 r 是模型集合中的模型总数, m(k) 是时间间 隔 (k − 1, k] 内起作用模型的索引 (标记), µi(k) 是 第 i个 模 型 (i = 1, 2, 3,··· , r)在 时 间 间 隔 (k − 1, k] 内起作用的概率. 因此有: µi(k) P{m(k) = i|zk}. (31) 其 中, zk表 示 k 时 刻 以 前 (包 括k时 刻) 的 所 有 观 测的集合. 假设各个模型之间的转移符合马尔可 夫 (Markov) 规律, 则模型转移概率可以表示为: pij P{m(k) = j|m(k − 1) = i}. (32) 记 k 时刻用第 i 个模型滤波得到的状态估计和相应 的协方差矩阵分别为 ˆxj(k) 和Pj(k). IMM估计器主要由以下4个步骤组成[3,9,10,11]: 1) 模型的交互输入. k 时刻模型 j 的初始条件可以通过交互 k − 1 时 刻各模型滤波器的状态估计得到. 即 ˆxi(k − 1)µi|j(k − 1), (33) j(k − 1) r ˆx0 i=1 式中 µi|j(k − 1) = P{m(k − 1) = i|m(k) = j, zk−1} = pijµi(k − 1) (34) pljµl(k − 1) , i, j = 1, 2,··· , r, r j (k − 1)= P 0 l=1 表示模型交互概率. 与式(33)对应的协方差为: r µi|j(k − 1){Pi(k−1)+[ˆxi(k−1)− i=1 j(k − 1)]T}. j(k − 1)][ˆxi(k − 1) − ˆx0 ˆx0 (35) 2) r 个模型并行滤波.
    834 控 制 理 论 与 应 用 第 25 卷 运 动; 200∼250 s期 间 在 C 点 做 逆 时 针 协 同 转 弯 运动, 此时的初始加速度向量为(16m/s2, 28m/s2, −14m/s2) (称 为C1弯), 或 者 为(36m/s2, 48m/s2, −24m/s2) (称为C2弯)且相对B点数值更大, 与速度 向量也不垂直, 即 C1 或 C2 弯均不符合 3DCSCT 模 型的前提假设; 之后目标匀速运动到D点. 根据 Kalman 滤波或其他滤波方法的单循环运 算步骤, 以及步骤1)中求出的 k 时刻模型初始条 j (k − 1), 可以计算出第 j 个模型 j(k − 1) 和 P 0 件 ˆx0 的状态估计 ˆxj(k) 和协方差 Pj(k). 同时还可以进一 步求出 k 时刻每个模型的似然函数. Λj(k) p{z(k)|m(k) = j, zk−1} = N[υj(k); 0, Sj(k)]. (36) 其 中υj(k) 和 Sj(k) 是 量 测 “残 差” 及 其 协 方 差. N[r; 0, Q] 表示服从正态分布随机变量 r 的概率 密度函数, 并且其均值为0, 协方差矩阵为Q. 3) 模型概率更新. µj(k) = Λj(k) r r c i=1 l=1 其中c为归一化常数, 并能通过式(38)计算. Λi(k)pliµl(k − 1). c = r l=1 pijµi(k − 1). (37) (38) r r j=1 4) 状态估计与协方差组合. k 时刻滤波器组对目标状态的最终估计及其 协方差矩阵可以通过组合各滤波器的估计结果由 式(39)(40)得到. ˆx(k) = ˆxj(k)µj(k), (39) P (k) = µj(k){Pj(k) + j=1 [ˆxj(k) − ˆx(k)][ˆxj(k) − ˆx(k)]T}. (40) 4 算算算法法法实实实现现现与与与仿仿仿真真真(Implementation and sim- ulation) 目标在三维空间做匀速直线运动时, CV 模型能 提供良好的跟踪精度: 3DCSCT 模型在加入了运动 约束后能对协同转弯提供良好的跟踪性能; 其他3个 模型对加速度反应敏感, 同时因为 3DCSCT 模型中 的参数需要由加速度和速度的比值估计, 因此良好 的加速度估计能力不但能保证跟踪算法对目标机动 的响应灵敏度, 而且对目标转弯运动估计精度的提 高有很大的帮助. 本文从 CV 模型、CA 模型、Singer模型、CSM 模 型与 3DCSCT 模型中选择不同的组合, 用 IMM 方 法跟踪三维高机动目标. 4.1 仿仿仿真真真情情情景景景(Simulation scenarios) 设目标飞行轨迹如图1所示, 目标从 A(30 km, 30 km, 30 km)出发, 0∼50 s做匀速直线运动; 50∼ 100 s期间在 B 点做顺时针协同转弯, 初始加速度 为(10m/s2, −12m/s2, 2m/s2), 此时的加速度向量 和速度向量垂直, 即 B 弯符合 3DCSCT 模型假设; 过 B弯 后, 在100∼200 s内 目 标 仍 然 做 匀 速 直 线 图 1 三维机动目标轨迹 3D maneuvering target trajectory Fig. 1 假设传感器能得到目标在 x − y − z 3个方向的 位置量测数据, 量测标准差为400 m, 目标运动的过 程噪声为白噪声. 滤波器参数设置为: Singer 模型 和 CSM 模型的机动时间常数 τ = 0.5; 模型初始化 概率 µ0 = ; 模型转移概率为: 0.8, 0.1, 0.1 0.98 0.02 0 0.7 0 0.05 0 0.3 0.95  . pij = 运动约束滤波 Ru = 800(0.92)k + 20m2/s4[8]. 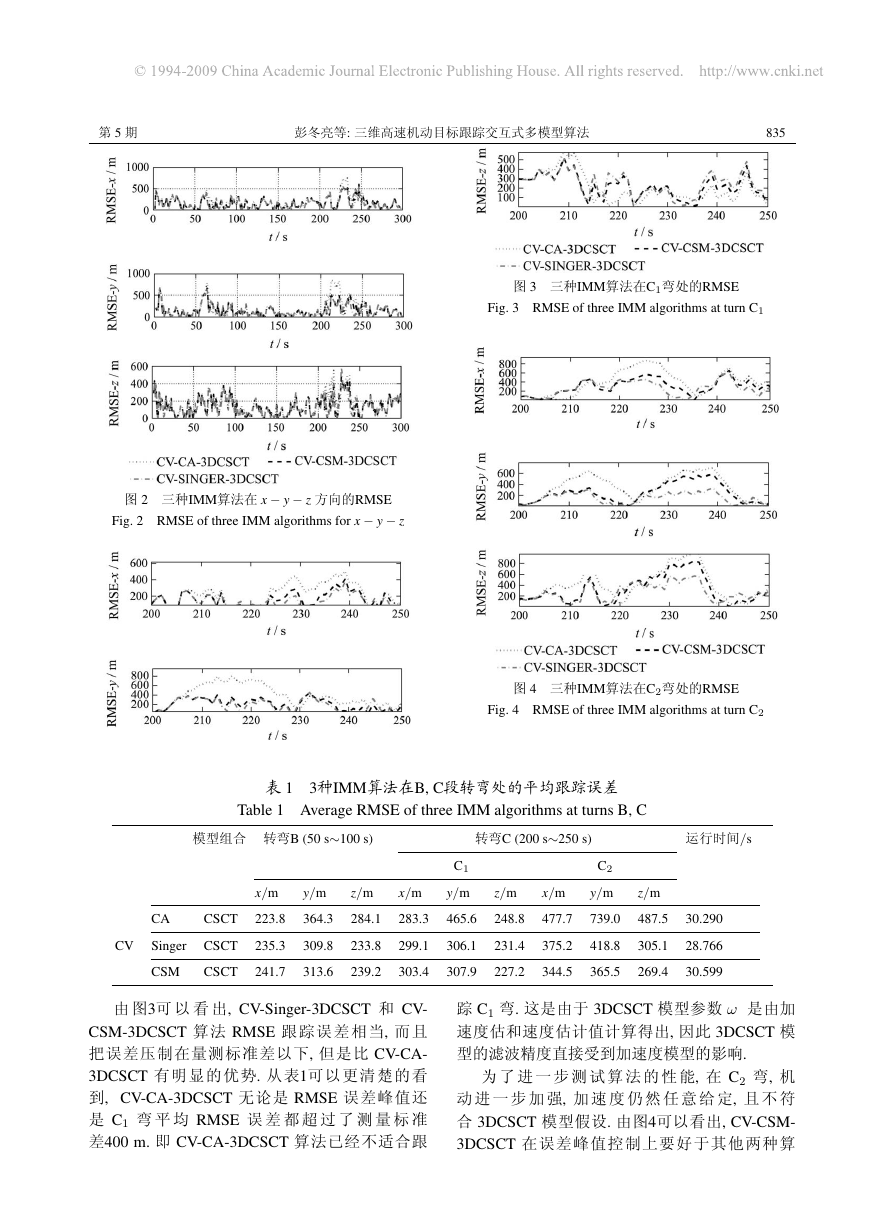4.2 仿仿仿真真真结结结果果果分分分析析析(Simulation results and analy- sis) 图2显示的是目标做 B、C1 转弯时3种组合算法 的RMSE曲线; 图3显示的是目标在 C1 弯 RMSE 跟 踪误差曲线, 即图2在200∼250 s的放大图; 图4显示 的是 C2 弯 RMSE 曲线; 表1是三组合算法在 B, C 两 个弯的平均 RMSE 和100次蒙特卡罗仿真下所需的 时间. 从图2来看, 在目标做匀速直线运动时, 3种组 合 算 法 的 性 能 相 当, 误 差 基 本 一 致; 在B弯, 所 给 的加速度较小, 而且与速度垂直, 符合3DCSCT模 型的假设. 3种算法的 RMSE 跟踪误差相差不大. 从 表1可 以 看 出, CV-Singer-3DCSCT 和 CV-CSM- 3DCSCT 平均 RMSE 误差保持在 3% 以内, 比 CV- CA-3DCSCT 算法稍好; 在 C1 弯时, 目标机动增 强, 转弯时给定的加速度也不符合 3DCSCT 的假设.
    第 5 期 彭冬亮等: 三维高速机动目标跟踪交互式多模型算法 835 图 3 三种IMM算法在C1弯处的RMSE Fig. 3 RMSE of three IMM algorithms at turn C1 图 2 三种IMM算法在 x − y − z 方向的RMSE Fig. 2 RMSE of three IMM algorithms for x − y − z 图 4 三种IMM算法在C2弯处的RMSE Fig. 4 RMSE of three IMM algorithms at turn C2 表 1 3种IMM算法在B, C段转弯处的平均跟踪误差 Table 1 Average RMSE of three IMM algorithms at turns B, C 模型组合 转弯B (50 s∼100 s) 转弯C (200 s∼250 s) 运行时间/s x/m y/m z/m x/m C1 y/m z/m x/m C2 y/m z/m CA CSCT 223.8 364.3 284.1 283.3 465.6 248.8 477.7 739.0 487.5 30.290 CV Singer CSCT 235.3 309.8 233.8 299.1 306.1 231.4 375.2 418.8 305.1 28.766 CSM CSCT 241.7 313.6 239.2 303.4 307.9 227.2 344.5 365.5 269.4 30.599 由 图3可 以 看 出, CV-Singer-3DCSCT 和 CV- CSM-3DCSCT 算法 RMSE 跟踪误差相当, 而且 把误差压制在量测标准差以下, 但是比 CV-CA- 3DCSCT 有明显的优势. 从表1可以更清楚的看 到, CV-CA-3DCSCT 无论是 RMSE 误差峰值还 是 C1 弯 平 均 RMSE 误 差 都 超 过 了 测 量 标 准 差400 m. 即 CV-CA-3DCSCT 算法已经不适合跟 踪 C1 弯. 这是由于 3DCSCT 模型参数 ω 是由加 速度估和速度估计值计算得出, 因此 3DCSCT 模 型的滤波精度直接受到加速度模型的影响. 为 了 进 一 步 测 试 算 法 的 性 能, 在 C2 弯, 机 动 进 一 步 加 强, 加 速 度 仍 然 任 意 给 定, 且 不 符 合 3DCSCT 模型假设. 由图4可以看出, CV-CSM- 3DCSCT 在误差峰值控制上要好于其他两种算
    控 制 理 论 与 应 用 第 25 卷 836 法. 由表1也可看到在加速度最大的 y 轴上, 平 均 RMSE 误差有 15% 到 50% 的优势; 而且也只 有 CV-CSM-3DCSCT 把平均 RMSE 误差控制在 测量标准差之下. 当然, 由于所给的加速度的数值 较大, 3种算法的误差峰值都超过了400 m. 在同等条件下, 100次蒙特卡罗仿真3种算法 的时间差距在 5% 以内, 分别为30.29 s, 28.766 s, 30.599 s. 因此, 在计算量相当的情况下, CV-CSM- 3DCSCT 算法可以更有效的跟踪三维强机动目 标. 5 结结结论论论(Conclusions) 本 文 详 细 讨 论 了 三 维 高 机 动 目 标 的 运 动 模 型, 基于目标运动模型和交互式多模型方法提出 了一种常速模型、“当前” 统计模型、带约束的三 维常速率协同转弯模型的交互式多模型算法. 通 过与其他三维目标运动模型组合构成的交互式 多模型方法的仿真对比和分析表明: 由匀速模 型、“当前” 统计模型、常速转弯模型组成的交互 式三维机动目标跟踪算法更具实用性, 适合于三 维高速机动目标的跟踪. 参参参考考考文文文献献献(References): [1] LI X R, JILKOV V P. A survey of maneuvering target tracking: dy- namic models[C] // Proceedings of SPIE Vol 4048, Conference on Signal and Data Processing of Small Targets. Orlando: SPIE Press, 2000: 212 – 235. [2] BLOM H A, BAR SHALOM Y. The interacting multiple model al- gorithm for systems with markovian switching coefficient[J]. IEEE Transactions on Automatic Control, 1988, 33(8): 780 – 783. [3] WATSON G A, BLAIR W D. IMM algorithm for tracking targets that maneuver through coordinated turn[C] // Proceedings of SPIE Vol 1698, Conference on Signal and Data Processing of Small Tar- gets. Orlando: SPIE Press, 1992: 236 – 247. [4] NABAA N, BISHOP R H. Validation and comparison of coordinated turn aircraft maneuver models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(1): 250 – 259. [5] SINGER R A. Estimating optimal tracking filter performance for manned maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(4): 473 – 483. [6] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版 社, 1991. (ZHOU Hongren, JING Zhongliang, WANG Peide. Maneuvering Target Tracking[M]. Beijing: National Defense Industry Press, 1991.) [7] TAHK M, SPEYER J L. Target tracking problems subject to kine- matic constraints[J]. IEEE Transactions on Automatic Control, 1990, 35(3): 324 – 326. [8] ALOUANI A T, BLAIR W D. Use of a kinematic constraint in track- ing constant speed, maneuvering targets[J]. IEEE Transactions on Automatic Control, 1993, 38(7): 1107 – 1111. [9] BAR SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with Ap- plications to Tracking and Navigation: Theory, Algorithms, and Soft- ware[M]. New York: John Wiley & Sons, Inc, 2001. [10] LI X R, JILKOV V P. Survey of maneuvering target tracking-part V: multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255 – 1321. [11] KADIRKAMANATHAN V, LI P, KIRUBARAJAN T. Sequential Monte Carlo filtering vs. the IMM estimator for fault detection and isolation in nonlinear systems[C] // Proceedings of SPIE Vol. 4389, Conference on Component and Systems Diagnostics, Prognosis, and Health Management. Orlando: SPIE Press, 2001: 263 – 274. 作者简介: 彭彭彭冬冬冬亮亮亮 (1977—), 男, 博士, 副教授, 目前研究方向为信息融 合、目标跟踪、随机集方法及应用, E-mail: dlpeng@hdu.edu.cn; 郭郭郭云云云飞飞飞 (1978—), 男, 博士, 讲师, 目前研究方向为信息融合、目 标跟踪, E-mail: gyf@hdu.edu.cn; 薛薛薛安安安克克克 (1957—), 男, 博士, 教授, 博士生导师, 目前研究方向 为信息融合、鲁棒控制、优化调度, E-mail: akxue@hdu.edu.cn.
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料