论文研究-智能水下机器人滑模控制研究 .pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.43M 资料格式：pdf 举报版权申诉

第1页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第2页.png

第2页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第3页.png

第3页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第4页.png

第4页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第5页.png

第5页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第6页.png

第6页 / 共7页

weixin_39841365-11565482-论文研究智能水下机器人滑模控制研究.pdf-第7页.png

第7页 / 共7页

文本预览

中国科技论文在线 http://www.paper.edu.cn 智能水下机器人滑模控制研究徐璐瑜，张永林** （江苏科技大学电子信息学院，江苏省镇江市 212003） 5 摘要：针对智能水下机器人运动轨迹跟踪的问题，本文采用了基于指数趋近律和基于准滑动模态的滑模控制算法。通过对四自由度 AUV 系统模型进行可控正则化，将系统模型分成四个子系统，从而为每个子系统设计独立的滑模控制器。仿真结果表明基于准滑动模态的滑模控制能够很大程度地削弱抖振，较好地跟踪系统的运动轨迹，具有良好的控制效果。关键词：智能水下机器人；轨迹跟踪；滑模控制中图分类号：TP24 10 Research on sliding mode control of Autonomous 15 20 25 30 35 40 45 Underwater Vehicle XU Luyu, ZHANG Yonglin (School of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang Jiangsu 212003) Abstract: In order to realize the motion trajectory tracking of Autonomous Underwater Vehicle, this paper adopted sliding mode control algorithm based on index reaching law and quasi-sliding mode. Through the controllable regularization of the four-degree of freedom AUV system model, the system model is divided into four subsystems, thus independent sliding mode controller for each subsystem was designed. The simulation results show that the sliding mode controller based on quasi-sliding mode well weakens the chattering and get good performance in trajectory tracking. Key words: Autonomous Underwater Vehicle; trajectory tracking; sliding mode control 0 引言在过去的半个多世纪里，水下机器人技术得到了全面的发展，在海洋资源的开采和海底空间的探索上得到了广泛的应用，智能水下机器人（AUV）的研究和开发也越来越受到人们的重视。智能水下机器人是一个具有高度非线性、时变性和强耦合性的系统，要对其进行精确的数学建模并进行控制是及其困难的，要达到较好的控制效果，所采用的控制方法需要摆脱对精确数学模型的依赖,此外还得具有良好的自适应性和鲁棒性。滑模控制、模糊控制、自适应控制、神经网络控制等智能控制方法设计 AUV 控制器能获得良好的控制效果，是目前主要的研究方向。 Xu 提出了一种模糊滑模控制器用于 AUV 的轨迹跟踪和定位问题，该控制器基于系统动力学的分解形式，使用模糊逻辑来动态调节滑模控制中的增益系数来消除抖振[1]。Huang 等将滑模切换函数作为 RBF 的输入进行学习并且输出到滑模控制器中实现单输入单输出的神经网络滑模控制[2]。Zhang 等提出了一种神经网络自适应滑模控制方法，对水下机器人的深度这一个自由度进行了跟踪控制[3]。刘云龙等采用具有光滑性和饱和性的 S 型函数来削弱滑模控制的抖振，提出了一种水下机器人软变结构控制，对水下机器人的深度进行了轨迹跟踪的控制[4]。王青山研究了海流环境下的 AUV 滑模控制，对水下机器人进退、艏摇、纵倾三个自由度方向的进行跟踪控制，采用一种新型的指数趋近律来削弱系统的抖振，取得了很好的控制效果[5]。H. Akcakaya 等用双曲正切三角函数代替指数趋近律中的符号函数，设计了基于指数趋近律的滑模控制器来跟踪 AUV 的运动轨迹，并与传统的 PID 控制进行了比较 [6]。通信联系人：张永林（1972-），男，副教授，东南大学博士，硕士生导师，主要从事船舶自动化和现代测控技术的研究. E-mail: just3zyl@qq.com 作者简介：徐璐瑜（1988-），男，硕士研究生，主要从事智能控制方向的研究 - 1 -

中国科技论文在线 http://www.paper.edu.cn 本文设计了基于指数趋近律和基于准滑动模态的滑模控制器，对智能水下机器人进退、横移、升沉和艏摇四个自由度方向上的运动轨迹进行了跟踪控制。通过仿真分析和对比表明基于准滑动模态的滑模控制器能很好地削弱抖振，在轨迹跟踪上性能良好。 1 水下机器人的动力学模型 50 水下机器人是一个复杂的非线性动力学系统，其数学模型是部分未知的，并受外界环境和自身状态变化的影响，要想准确地建立其数学模型几乎是不可能的，通常需要选择合适的方法得到简化的系统模型。 1.1 水下机器人所受合外力 55 智能水下机器人在水中所受到的合外力（矩）大致可分成三类[7]：第一类是作用在水下机器人上的水动力。水下机器人在水中运动，艇体、舵、翼和螺旋桨等推动周围的水产生运动，同时，水对机器人本体也产生反作用力，这种反作用力称为水动力。第二类是非流体动力，又称为静力，包括水下机器人所受的重力和浮力。第三类是水下机器人运动时执行机构产生的合推力，包括：推力器推力、舵的力、翼的力。此外，风、浪、流等也会对水下机器人产生外界环境干扰力。 60 1.2 AUV 的状态矩阵方程六自由度智能水下机器人的动力学方程为： (1) 其中，表示动坐标系下水下机器人的位置和动系相对于定系水下机器人的姿态角，为水下机器人受到的非惯性水动力，包括推力器推力、舵的力、 65 翼的力、重力与浮力的合力及外界环境干扰力等。为水下机器人载体的惯性矩阵。、均与水下机器人艇体水动力系数有关。假设水下机器人自身是静力平衡的，重力与浮力相互抵消，并认为风、浪、流等外界环境产生的干扰力对水下机器人的运动影响很小。所以就是推力器推力、舵的力、翼的力。惯性矩阵是非奇异的，用表示，由式(1)可得简化的六 70 自由度 AUV 空间运动的状态矩阵方程： (2) 本文以一个六自由度的小型智能水下机器人为例[8]进行仿真研究，仅考虑前进、横移、升沉和艏摇四个方向上 AUV 的运动，所研究的系统实际上是一个四自由度的水下机器人。因此，可对式(2)进行简化，有，，。 75 惯性矩阵和可写成以下形式： (3) - 2 - veMqFFT[,,,,,]xyzqvFeFMvFMeFMeFT[,,,,,]XYZKMN1()vqMFT[,,,]xyzqT[,,,]uvwrqT[,,,]XYZNMT[,,,]vvisvisvisvisXYZNF0000000000vrwvruzmXmYYmZNINM

中国科技论文在线 http://www.paper.edu.cn (4) 其中，表示智能水下机器人载体的质量，表示绕轴的转动惯量，、、、等均为艇体水动力系数，它们都是已知的，一般通过试验获得。 80 2 AUV 滑模控制器设计 2.1 系统模型的可控正则化智能水下机器人是个各自由度运动强耦合的运动系统，因此可以采用分散的滑动模态切换模式来进行分析，分别为每个子系统设计一个独立的控制器，从而可以实现系统的分散解耦控制，对于每一个子系统，只含有一个与本子系统有关的控制量。 85 由智能水下机器人空间运动的状态矩阵方程(2)式，令，根据分散滑动模态的切换模式，可将系统模型分成四个子系统，写成可控正则型的标准的形式： (5) 其中，，。 2.2 切换函数的设计 90 位置控制器的输入是位置偏差和偏差的变化率，假设智能水下机器人的期望轨迹为：，，，。则第个子系统的轨迹跟踪误差为： (6) 95 对于可控正则型的非线性系统，构造线性切换函数： (7) 其中，，为待定系数，。则第个子系统的切换面为： 100 由于切换函数是线性的，所以可以通过极点配置法来确定待定系数。式(8)的极点为： (8) (9) - 3 - 22220 visvisrvisvisXmvrXuXrXuuurruuYmurYurYvvvvZZuZuwZwZwwwwwwNurNuvNrrvrruwNrmzIozuXuuXvYvNiuT[,]iiiqq=x00010()001iiiiiiquqxxx000011234[(),(),(),()]vxxxxMF11234[,,,]uuuuuMτdeqqdeqq111dddddqxuqx222dddddqyvqx333dddddqzwqx444dddddqrqxiiidiiidiidqqqqe=xxTT123411223344[,,,][,,,]ssssscececece[,1]iiccic1,2,3,4ii0iiiiiisceeceiic

中国科技论文在线 http://www.paper.edu.cn 要保证系统的稳定性，则有。考虑到 AUV 在运动过程中，一般对进退、横移、升沉方向上的运动响应要求较快，对横艏摇的运动响应稍慢，因此在为各子系统进行极点配置时，应保证、、取值较大，而取值较小。给系统进行极点配置后，便可得到系统的切换函数： 105 (10) 2.3 滑模控制器的设计采用基于指数趋近律的滑模控制器来对 AUV 系统进行控制时，切换函数有如下形式： (11) 110 其中，。由和式(2)可知： (12) 联立式(11)和式(12)可得： 115 求解上式可得智能水下机器人的控制力： (13) (14) 因此滑模控制器的输出为： (15) 基于指数趋近律的滑模控制可以同时满足切换面的存在条件、到达条件和稳定条件， 120 但系统存在较明显的抖振。为了削弱抖振，本文设计了基于准滑动模态的滑模控制器对系统进行控制，用饱和函数来代替符号函数，在边界层外采用常规滑模控制，在边界层内用连续状态的反馈控制。符号函数的数学表达式如下： (16) 其中称为边界层。 125 因此，由式(15)可得采用准滑动模态的滑模控制器的输出为： (17) 3 仿真研究 3.1 AUV 的主要参数本文仅考虑前进、横移、升沉和艏摇四个方向上 AUV 的运动，对 AUV 的运动进行轨 130 迹跟踪，验证滑模控制算法的有效性，某小型 AUV 的主要参数如下[8]： - 4 - 0i1c2c3c4c1234diag[,,,]ccccseeceesgn()=--ssks1234diag[,,,]1234diag[,,,]kkkkk=+scee1()vd=++sceeceMFq1()sgn()vd+ceMFqsks[sgn()]vdMqceεsksF1[sgn()]vduqceεsksMF=sat()ssgn()ssat()s1sat()||1sssss1[sat()]vduqceεsksMF=

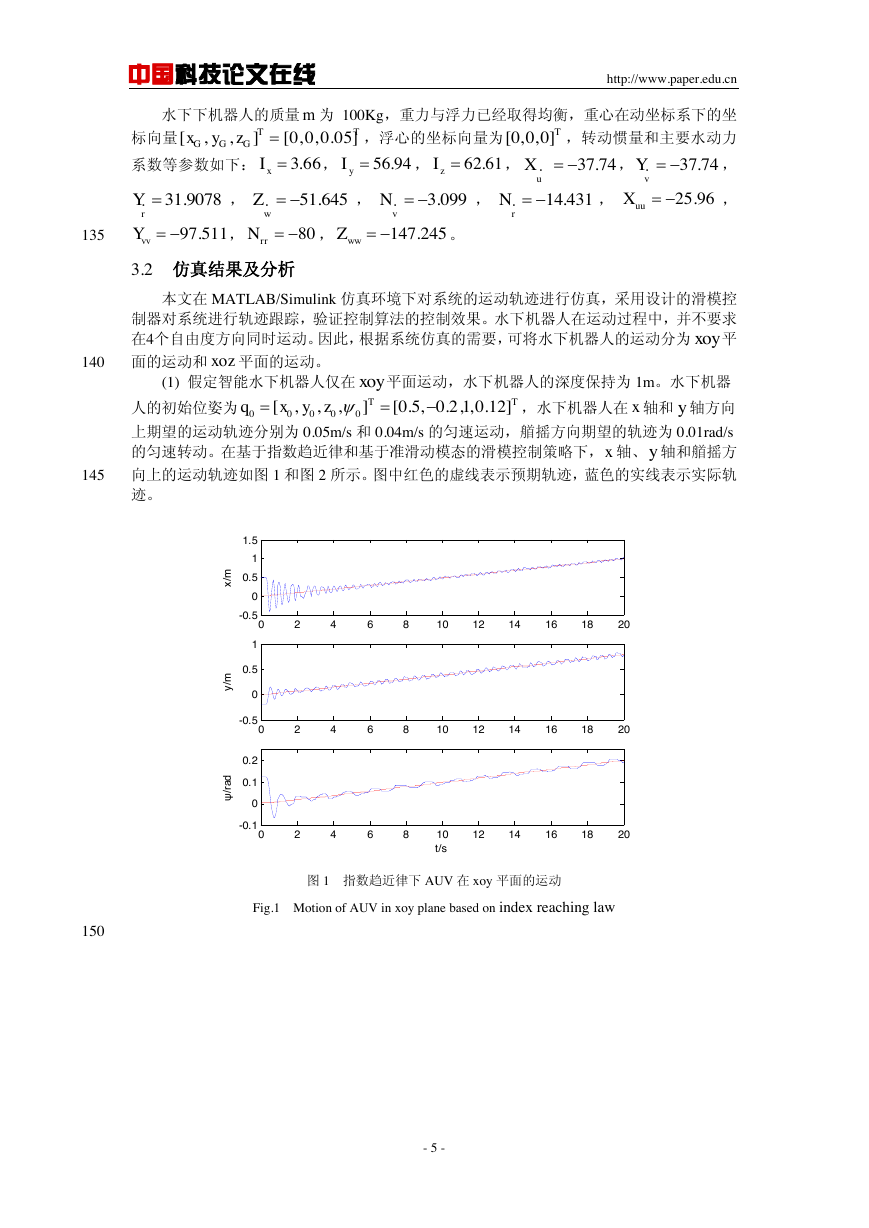
中国科技论文在线 http://www.paper.edu.cn 水下下机器人的质量为 100Kg，重力与浮力已经取得均衡，重心在动坐标系下的坐，转动惯量和主要水动力，浮心的坐标向量为标向量 135 140 145 150 系数等参数如下：，，，，，，，，。 3.2 仿真结果及分析，，，，本文在 MATLAB/Simulink 仿真环境下对系统的运动轨迹进行仿真，采用设计的滑模控制器对系统进行轨迹跟踪，验证控制算法的控制效果。水下机器人在运动过程中，并不要求在4个自由度方向同时运动。因此，根据系统仿真的需要，可将水下机器人的运动分为平面的运动和 (1) 假定智能水下机器人仅在平面运动，水下机器人的深度保持为 1m。水下机器平面的运动。人的初始位姿为，水下机器人在轴和轴方向上期望的运动轨迹分别为 0.05m/s 和 0.04m/s 的匀速运动，艏摇方向期望的轨迹为 0.01rad/s 的匀速转动。在基于指数趋近律和基于准滑动模态的滑模控制策略下，轴、轴和艏摇方向上的运动轨迹如图 1 和图 2 所示。图中红色的虚线表示预期轨迹，蓝色的实线表示实际轨迹。图 1 指数趋近律下 AUV 在 xoy 平面的运动 Fig.1 Motion of AUV in xoy plane based on index reaching law - 5 - mT[,,][0,0,0.05]GGGxyzT[0,0,0]3.66xI56.94yI62.61zI37.74uX37.74vY31.9078rY51.645wZ3.099vN14.431rN25.96uuX97.511vvY80rrN147.245wwZxoyxozxoyTT00000[,,,][0.5,0.2,1,0.12]xyzqxyxy02468101214161820-0.500.511.5x/m02468101214161820-0.500.51y/m02468101214161820-0.100.10.2t/sψ/rad

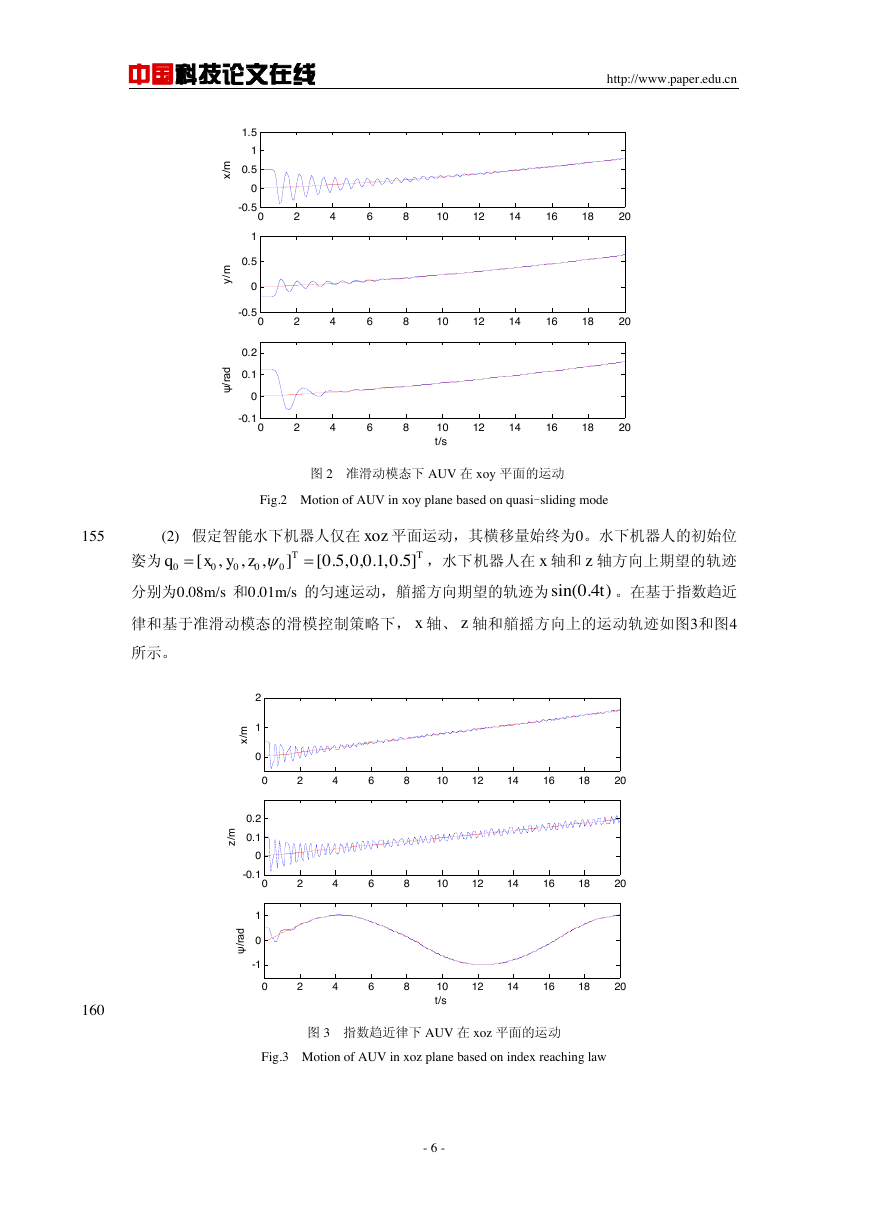
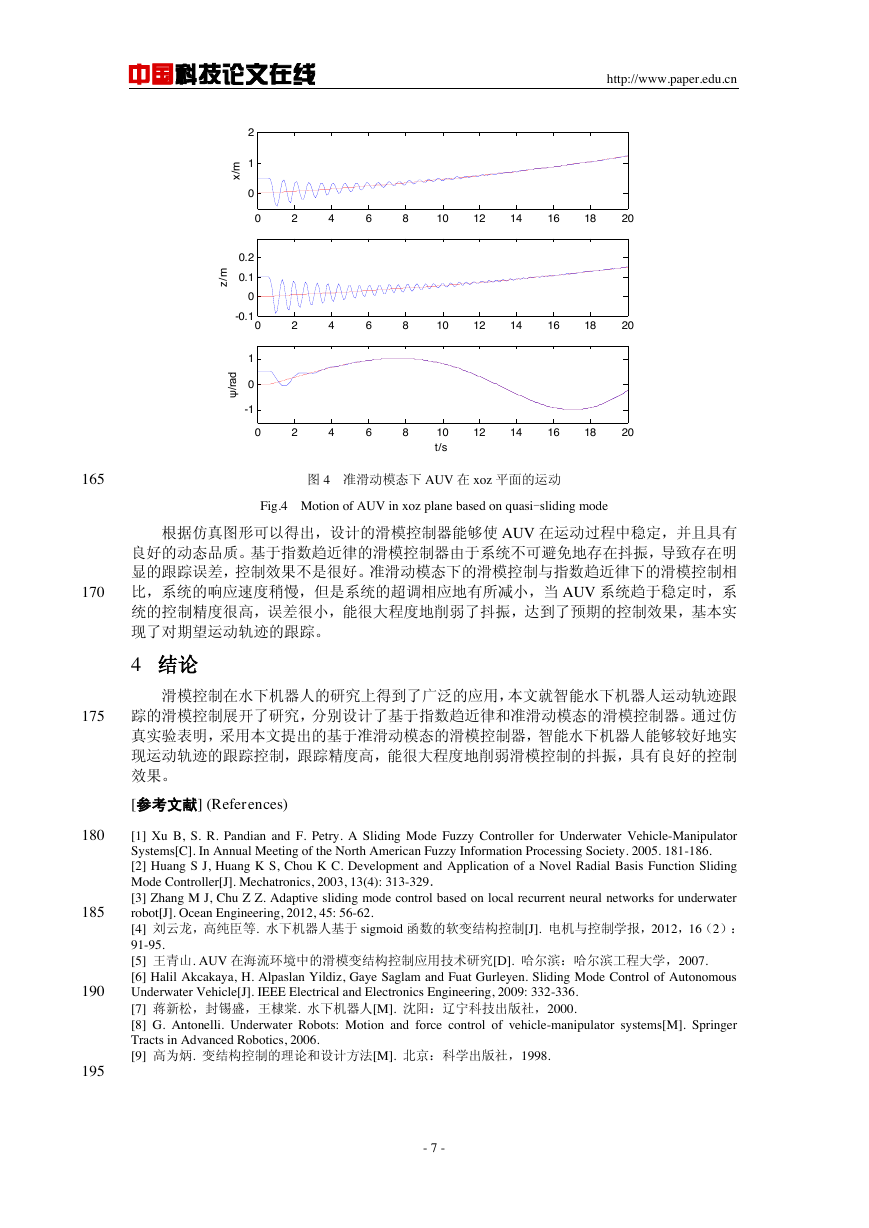
中国科技论文在线 http://www.paper.edu.cn 图 2 准滑动模态下 AUV 在 xoy 平面的运动 Fig.2 Motion of AUV in xoy plane based on quasi-sliding mode 155 (2) 假定智能水下机器人仅在平面运动，其横移量始终为0。水下机器人的初始位姿为，水下机器人在轴和轴方向上期望的轨迹分别为0.08m/s 和0.01m/s 的匀速运动，艏摇方向期望的轨迹为。在基于指数趋近律和基于准滑动模态的滑模控制策略下，轴、轴和艏摇方向上的运动轨迹如图3和图4 所示。 160 图 3 指数趋近律下 AUV 在 xoz 平面的运动 Fig.3 Motion of AUV in xoz plane based on index reaching law - 6 - 02468101214161820-0.500.511.5x/m02468101214161820-0.500.51y/m02468101214161820-0.100.10.2t/sψ/radxozTT00000[,,,][0.5,0,0.1,0.5]xyzqxzsin(0.4)txz02468101214161820012x/m02468101214161820-0.100.10.2z/m02468101214161820-101t/sψ/rad

中国科技论文在线 http://www.paper.edu.cn 图 4 准滑动模态下 AUV 在 xoz 平面的运动 Fig.4 Motion of AUV in xoz plane based on quasi-sliding mode 根据仿真图形可以得出，设计的滑模控制器能够使 AUV 在运动过程中稳定，并且具有良好的动态品质。基于指数趋近律的滑模控制器由于系统不可避免地存在抖振，导致存在明显的跟踪误差，控制效果不是很好。准滑动模态下的滑模控制与指数趋近律下的滑模控制相比，系统的响应速度稍慢，但是系统的超调相应地有所减小，当 AUV 系统趋于稳定时，系统的控制精度很高，误差很小，能很大程度地削弱了抖振，达到了预期的控制效果，基本实现了对期望运动轨迹的跟踪。 4 结论滑模控制在水下机器人的研究上得到了广泛的应用，本文就智能水下机器人运动轨迹跟踪的滑模控制展开了研究，分别设计了基于指数趋近律和准滑动模态的滑模控制器。通过仿真实验表明，采用本文提出的基于准滑动模态的滑模控制器，智能水下机器人能够较好地实现运动轨迹的跟踪控制，跟踪精度高，能很大程度地削弱滑模控制的抖振，具有良好的控制效果。 [参考文献] (References) [1] Xu B, S. R. Pandian and F. Petry. A Sliding Mode Fuzzy Controller for Underwater Vehicle-Manipulator Systems[C]. In Annual Meeting of the North American Fuzzy Information Processing Society. 2005. 181-186. [2] Huang S J, Huang K S, Chou K C. Development and Application of a Novel Radial Basis Function Sliding Mode Controller[J]. Mechatronics, 2003, 13(4): 313-329． [3] Zhang M J, Chu Z Z. Adaptive sliding mode control based on local recurrent neural networks for underwater robot[J]. Ocean Engineering, 2012, 45: 56-62. [4] 刘云龙，高纯臣等. 水下机器人基于 sigmoid 函数的软变结构控制[J]. 电机与控制学报，2012，16（2）： 91-95. [5] 王青山. AUV 在海流环境中的滑模变结构控制应用技术研究[D]. 哈尔滨：哈尔滨工程大学，2007. [6] Halil Akcakaya, H. Alpaslan Yildiz, Gaye Saglam and Fuat Gurleyen. Sliding Mode Control of Autonomous Underwater Vehicle[J]. IEEE Electrical and Electronics Engineering, 2009: 332-336. [7] 蒋新松，封锡盛，王棣棠. 水下机器人[M]. 沈阳：辽宁科技出版社，2000. [8] G. Antonelli. Underwater Robots: Motion and force control of vehicle-manipulator systems[M]. Springer Tracts in Advanced Robotics, 2006. [9] 高为炳. 变结构控制的理论和设计方法[M]. 北京：科学出版社，1998. 165 170 175 180 185 190 195 - 7 - 02468101214161820012x/m02468101214161820-0.100.10.2z/m02468101214161820-101t/sψ/rad

分享到：

赞收藏

资料库

论文研究-智能水下机器人滑模控制研究 .pdf

相关推荐

开发技术

热门标签

最新资料